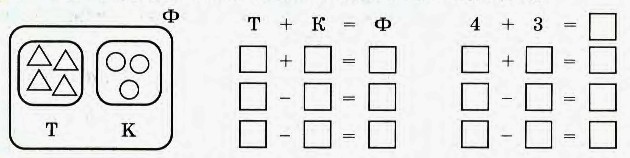значения каких выражений являются четными числами

Методическая разработка «Готовимся к олимпиаде по математике. ЧЁТНОСТЬ»

ГОТОВИМСЯ К ОЛИМПИАДЕ ПО МАТЕМАТИКЕ

I. Чётность суммы и произведения двух чисел

Значит, числа 10, ( − 6) и 0 являются чётными, а число 15 – нечётным.

Как формально можно записать, что заданное число является чётным (или нечётным)? Иными словами, как можно записать тот факт, что число является чётным (или нечётным), с помощью математических символов?

1) Если число n – чётное, то его можно записать в виде

2) Если число n – нечётное, то его можно записать в виде

Можно заметить, что чётные и нечётные числа на координатной прямой чередуются. Поэтому, сдвинувшись на один шаг от чётного числа, мы попадём в нечётное.

Как понятия чётного и нечётного числа взаимодействуют с арифметическими операциями (а именно, с операциями сложения, вычитания и умножения)?

Нетрудно убедиться, что при сложении чётного числа с нечётным мы получаем нечётную сумму. Например, 8 + 9 = 17.

Докажем это утверждение для произвольных целых чисел.

Пусть n ₁ – чётное число, а n ₂ – нечётное.

Тогда эти числа можно записать так:

Сложив эти два числа, мы получим следующую запись:

Чётное число + нечётное число = 2 ∙ k ₁ + ( 2 ∙ k ₂ + 1) = 2 ∙ k ₁ + 2 ∙ k ₂ + 1 =

= 2 ∙ ( k ₁ + k ₂ ) + 1 = чётное число + 1 = нечётное число

Аналогично можно доказать, что при сложении двух чётных чисел получается чётная сумма:

Чётное число + чётное число = 2 ∙ k ₁ + 2 ∙ k ₂ = 2 ∙ k ₁ + 2 ∙ k ₂ =

= 2 ∙ ( k ₁ + k ₂ ) = чётное число.

Также легко убедиться, что при сложении двух нечётных чисел также получается чётное число:

Нечётное число + нечётное число = ( 2 ∙ k ₁ +1) + ( 2 ∙ k ₂ + 1) = 2 ∙ k ₁ + 2 ∙ k ₂ + 1 + 1 =

= 2 ∙ ( k ₁ + k ₂ ) + 2 = чётное число + чётное число = чётное число.

При вычитании двух нечётных чисел чётность разности определяется так же, как и при их сложении.

Полученные результаты можно оформить в виде таблицы сложения чётных и нечётных чисел:

Заполним такую же таблицу для операции умножения:

1) чётное число ∙ чётное число = ( 2 ∙ k ₁ ) ∙ ( 2 ∙ k ₂ ) = 2 ∙ (2 k ₁ ∙ k ₂ ) = чётное число;

2) чётн. число ∙ нечётн. число = ( 2 ∙ k ₁ ) ∙ ( 2 ∙ k ₂ + 1) = 2 ∙ ( k ₁ ∙ (2 k ₂ + 1)) = чётное число;

3) нечётн. число ∙ нечётн. число = ( 2 ∙ k ₁ + 1) ∙ ( 2 ∙ k ₂ + 1) = 2 k ₁ ∙ 2 k ₂ + 2 k ₁ + 2 k ₂ + 1 ) =

= чётное число + чётное число + чётное число + нечётное число = нечётное число.

II. Чётность суммы и произведения нескольких чисел

Произведение нескольких целых чисел нечётно, если и только если все сомножители нечётны.

Сумма нескольких чисел нечётна, если и только если в неё входит нечётное число нечётных слагаемых.

III. Решение задач. Задачи для самостоятельного решения

1. Будем обозначать через Ч произвольное чётное число, а через Н — произвольное нечётное число. Выберите все выражения, значения которых являются чётными.

2. Не вычисляя значений выражений, выберите все, значения которых являются чётными.

2) (5 + 6) ⋅ (7 + 8) + (9 + 11) ⋅ (10 + 12),

3) (3 + 4) ⋅ (5 + 6) ⋅ (7 + 8) ⋅ (9 + 10),

4) (1 + 2) ⋅ (3 + 5) − (8 + 9) ⋅ (10 + 12).

3. Значения каких выражений будут чётны при любом целом n?

4. Значения каких выражений будут чётны при любых целых m и n?

5. Выберите все верные утверждения.

1) Сумма 11 нечётных чисел всегда чётна.

2) Сумма 11 нечётных чисел может быть чётна, а может быть нечётна.

3) Сумма 11 нечётных чисел всегда нечётна.

4) Сумма 10 нечётных чисел всегда чётна.

5) Сумма 10 нечётных чисел может быть чётна, а может быть нечётна.

6) Сумма 10 нечётных чисел всегда нечётна.

6. Не вычисляя значений выражений, выберите все, значения которых являются чётными.

7. Известно, что произведение abc нечетно. Какие из следующих чисел заведомо являются четными?

6) (а + 1) ∙ (b + 1) ∙ (c + 1).

8. Целые числа n1, n2, …, n10 таковы, что n1 ⋅ n2 ⋅ … ⋅ n10=1. Выберите все значения из списка, которые может принимать сумма n1+n2+…+n10.

9. Известно, что сумма 20 целых чисел n1, n2, …, n20 нечётна. Какие из следующих чисел заведомо чётные?

IV. Решение более сложных задач.

Каждая из этих сумм, по условию, чётна. Сложим все четыре записанные суммы:

Поскольку мы сложили изначально чётные суммы, то и данная сумма будет чётна. Но произведение нечётного числа 3 на сумму ( a + b + c + d ) будет чётна в том и только в том случае, когда выражение в скобках представляет собой чётное число.

Задача 2. Существуют ли решения у ребуса АБ ⋅ Б = ЕВГ, если гласные буквы обозначают чётные цифры, а согласные — нечётные (одинаковые буквы обозначают одинаковые числа, а разные буквы — разные)?

По условию задачи, буквы А и Е соответствуют чётным цифрам, а буквы Б, В и Г – нечётным цифрам.

Заметим, что цифра В получается при умножении цифр А и Б. Но А число чётное, значит, это произведение – чётно.

Чтобы цифра В стала нечётной, необходимо, чтобы при умножении Б на Б получилось число, большее 10. Это достигается только при Б = <5, 7, 9>. Но если Б = 5, то Б ∙ Б = 25, и тогда цифра Г также равна 5, что невозможно.

Если Б = 7, то Б ∙ Б = 49, и цифра 4 прибавляется к результату умножения цифр А и Б, равному чётному числу, и В опять будет чётной цифрой.

Аналогично, при Б = 9 получаем, что Б ∙ Б = 81, и цифра 8 прибавляется к результату умножения цифр А и Б, равному чётному числу, и В опять будет чётной цифрой.

Получается, что при любом нечётном значении цифры Б цифра В будет чётной, что противоречит условию задачи.

Следовательно, задача не имеет решения.

Задача 3. Можно ли 25 рублей разменять 10 монетами номиналом 1, 3 и 5 рублей?

Заметим, что каждая монета номиналом 1, 3 и 5 рублей представляет собой нечётное число рублей. Если сложить 10 нечётных чисел по 1, 3 и 5, то независимо от того, какие именно числа мы сложили, их сумма будет чётной (поскольку 10 нечётных чисел можно разбить на пять пар нечётных чисел, и в каждой из этих пар сумма будет чётной). А число 25 – число нечётное.

Следовательно, 25 рублей невозможно разменять 10 монетами номиналом 1, 3 и 5 рублей.

Задача 4. На доске написано следующее равенство:

Можно ли заменить каждую ∗ на один из знаков «+» или «−» так, чтобы получилось верное равенство?

Нам нужно сложить десять целых чисел, среди которых имеется ровно пять чётных и ровно пять – нечётных.

Заметим, что после сложения данных десяти чисел мы должны получить число 0, которое является чётным.

Но сумма пяти чётных чисел равна чётному числу, а сумма пяти нечётных чисел – нечётному числу. Таким образом, сумма всех десяти данных чисел должна равняться нечётному числу, и следовательно, равняться нулю она не может.

Задача 5. Можно ли представить число 1 в виде суммы десяти дробей вида , где n — нечётное натуральное число?

Предположим, что 1 можно представить в виде суммы десяти таких дробей.

Тогда сумма данных дробей равна:

+ + + + + + + + + =

= .

Заметим, что каждое слагаемое в числителе – это произведение 9-ти нечётных множителей (а если в произведении нет ни одного чётного числа, то оно равно нечётному числу), и таких слагаемых там содержится ровно 10. Таким образом, сумма десяти нечётных чисел в числителе – это число чётное.

А вот знаменатель представляет собой произведение, составленное десятью множителями, среди которых также нет ни одного чётного числа, и поэтому этот знаменатель равен нечётному числу.

Мы получили дробь, в которой числитель – число чётное, а знаменатель – число нечётное, то есть числитель не равен знаменателю. Но дробь может быть равна 1 тогда и только тогда, когда числитель равен знаменателю.

= ≠ 1.

Значит, 1 нельзя представить в виде суммы дробей вида с нечётными знаменателями.

Задача 6. Незнайка выписал по кругу 11 натуральных чисел. Для каждых двух соседних чисел он посчитал их разность (из большего вычел меньшее). В результате среди найденных разностей оказалось четыре единицы, четыре двойки и три тройки. Докажите, что Незнайка где-то допустил ошибку.

Источник

Значения каких выражений являются четными числами

Числа, которые делятся на 2, называются чётными. Например: 2, 8, 14, 20.
Числа, которые не делятся на 2, называются нечётными. Например: 3, 5, 11, 17.

1. Запиши все чётные и нечётные числа от 1 до 20.

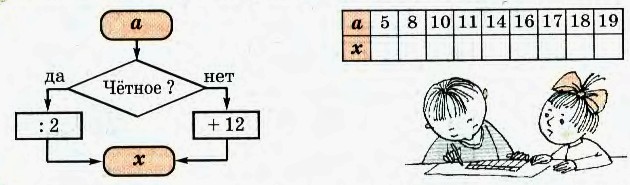
2. Заполни таблицу по алгоритму, заданному блок-схемой:

а) У Насти было 15 руб. Она заплатила за сок 3 монеты по 2 руб. Сколько денег у неё осталось?
б) В вагоне 9 купе по 2 места в каждом. Занято 14 мест. Сколько свободных мест?
в) В парке посадили 7 дубов и 2 ряда лип по 5 R ряду. Сколько всего деревьев посадили?
г) в двух подъездах дома по 8 квартир и по 1 квартире сторожа. Сколько всего квартир в этих подъездах?

Почему сначала выполняют умножение, а потом сложение и вычитание?

«У каждого из 7 учеников было по а тетрадей. Учитель раздал им поровну b тетрадей. Сколько тетрадей стало у каждого ученика?»

Докажи, что значение данного выражения при а = 3, b = 14 является нечётным числом.

(Вначале выполняют умножение и деление, а потом — сложение и вычитание.)

6. Составь все буквенные и числовые равенства по рисунку:

7. Найди значение суммы 396 + 284 и проверь решение тремя разными способами.

7 * 8 * 69 = 84 25 * 9 * 7 = 23 74 * 6 * 8 = 60

9*. Лестница состоит из 15 ступенек. На какую ступеньку надо встать, чтобы быть посередине лестницы? Какая ступенька будет средней у лестницы в 20 ступенек?

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Источник