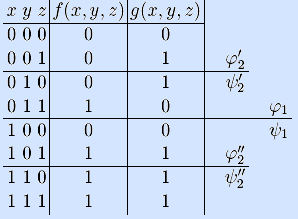какая булева функция является монотонной
МОНОТОННАЯ БУЛЕВА
ФУНКЦИЯ — булева функция 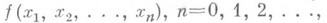
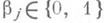
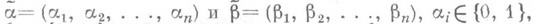

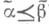
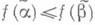

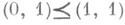
Примеры М. б. ф.: константы 0 и 1, тождественная функция 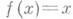

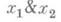
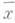

Полезное
Смотреть что такое «МОНОТОННАЯ БУЛЕВА» в других словарях:
Булева функция — В данной статье или разделе имеется список источников или внешних ссылок, но источники отдельных утверждений остаются неясными из за отсутствия сносок … Википедия
АЛГЕБРА ЛОГИКИ — раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логич. значений (истинности пли ложности), и логич. операций над ними. А. л. возникла в сер. 19 в. в трудах Дж. Буля (см. [1], [2]) и развилась затем в работах Ч … Математическая энциклопедия
Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия
 Раздел 1. Математическая логика
Раздел 1. Математическая логика
 Тема 1. Логика высказываний
Тема 1. Логика высказываний
 Тема 2. Булевы функции
Тема 2. Булевы функции
В этой теме рассматриваются всюду определенные функции, заданные на множестве B=<0,1>. Такие функции называются булевыми. Основная цель темы – доказать критерий полноты класса функций – теорему Поста.
 §1. Замкнутость и полнота
§1. Замкнутость и полнота
 §2. Самодвойственные функции
§2. Самодвойственные функции
 §3. Монотонные функции
§3. Монотонные функции
На множестве B= <0,1>в этом параграфе будем смотреть, как на частично упорядоченное множество с отношением 0 1.
На множестве B n введем порядок прямого произведения, т.е.
для любых a1,…,an, b1,…,bn Î B. Например, (1,0,0,1) £ (1,0,1,1), (1,0,1,0) £ (1,0,1,1). В то же время, неверно, что (1,0,0,1) £ (1,0,1,0).
Определение. Функция f(x1,…,xn) называется монотонной, если для любых двух векторов a=(a1,…,an) и b=(b1,…,bn) из условия a £ b следует, что f(a) £ f(b).
Примерами монотонных функций являются q (x), i (x), x × y, x Ú y. Функции n (x), x ® y, x+y немонотонны.
Монотонность функции означает, что если в какой-то вершине диаграммы она принимает значение 1, то и всюду выше функция принимает то же значение 1. Функция f(x1,x2,x3)=x1+x2 × x3 монотонной не является, так как в вершине (1,1,0) она принимает значение 1, а в вершине (1,1,1), которая выше первой, принимает значение 0.
Класс всех линейных функций обозначим буквой М. Убедимся в том, что М – это замкнутый класс. Монотонность тождественной функции очевидна. Пусть f(x1,…,xn) Î M и y1,…,yn – новые переменные. Возьмем два набора значений переменных y1,…,yn : a=(a1,…,an), b=(b1,…,bn) таких, что a £ b. Но эти векторы будут наборами значений переменных x1,…,xn, и поэтому выполняется неравенство f(a) £ f(b). Это означает, что М замкнут относительно переименования аргументов.
gk(b1,…,bn))=h(b1,…,bn). (Знак неравенства поставлен в силу монотонности функции f). Мы доказали, что класс М замкнут относительно суперпозиции.
Следующее утверждение называется леммой о немонотонной функции.
Лемма. Пусть f(x1,…,xn) – немонотонная функция. Тогда замыкание класса K=
На этой цепи найдутся соседние точки c=(c1,…,cn) и d=(d1,…,dn) такие, что c d, f(c)=1 и f(d)=0. Поскольку c и d – соседние точки, то
Для удобства обозначений будем считать, что c1=…=ci-1=0,ci+1=…cn=1. Рассмотрим функцию g(x)=f( q (x),…, q (x),x; i (x),…, i (x)), где точка с запятой отделяет i-ю компоненту от (i+1)-ой. Ясно, что g(x) принадлежит замыканию класса K.
Какая булева функция является монотонной
Определение. Булева функция f(x1, …, xn) называется монотонной (принадлежит классу M), если для любой пары наборов α и β таких, что α
Примеры. Исследуем мажоритарную булеву функцию.
Перебор пар начнем с наборов α=000 и β=001: для них α
Из элементарных булевых функций монотонными являются, например, конъюнкция и дизъюнкция. Не являются монотонными, например, штрих Шеффера и стрелка Пирса. •
В общем случае набор имеет несколько последователей, и для всех таких пар надо проверять выполнение условия монотонности. Чтобы сформулировать более простой алгоритм распознавания монотонной функции, докажем утверждение, которое к тому же будет использовано при доказательстве леммы о немонотонной функции.
Утверждение о условии немонотонности. Для любой пары наборов α и β таких, что α

Доказательство. Если α и β – соседи, то утверждение верно (α’=α, β’=β). Иначе вычислим расстояние d (по Хэммингу) между наборами α=a1… an и β=b1… bn и начнем строить цепочку наборов γ0, …, γd такую, что
и любые два расположенных рядом набора γi –1,γi (i=1, …, d) являются соседями. Очередной набор γi получим из предыдущего набора γi –1 заменой значения одной из ортогональных компонент наборов γi –1 и β (это будет замена 0 на 1, так как α
но тогда f(γd –1)=1 и f(β)=0, значит, условие немонотонности выполнится для последней пары: α’=γd –1 и β’=γd=β. •
Пример. Пусть задана пара булевых векторов 
Если f(α)>f(β), то смена значения функции с 1 на 0 произойдет по крайней мере на одной из четырех пар соседей. •
Алгоритм распознавания монотонной булевой функции (основан на утверждении о условии немонотонности).
Начало. Задана таблица истинности булевой функции.
Шаг 1. Сравниваем значения функции на наборах, соседних по первой переменной, то есть верхнюю половину столбца значений функции (вектор φ1) с нижней половиной (вектор φ1). Если условие φ1
Шаг 2. Сравниваем значения функции на наборах, соседних по второй переменной, то есть верхние четвертины столбца значений функции (векторы φ’2, φ»2) с нижними четвертинами (векторами φ’2, φ»2) в каждой половине. Если хотя бы одно из условий φ’2

Шаги 3 –n. Аналогично сравниваем восьмые, шестнадцатые части, и так далее. Если ни одно из проверяемых условий не нарушено, то функция монотонна.
Примеры. Рассмотрим две булевых функции (первая – мажоритарная).
Проверим на монотонность функцию g(x,y,z). Сравниваем половины столбца значений: φ1=0110 
Теорема о замкнутости класса M. Множество всех монотонных булевых функций является замкнутым классом.
Доказательство. Рассмотрим суперпозицию любых булевых функций из M, то есть функцию
и покажем, что она монотонна. Подставим в суперпозицию любую пару наборов α и β таких, что α
где γ и δ – булевы векторы. Так как α

Доказательство. Рассмотрим немонотонную функцию f(x1, …, xn). Согласно утверждению о условии немонотонности, существует пара соседних наборов α=a1… an и β=b1… bn таких, что α
Пусть α и β – соседи по k –й компоненте, тогда
Подставим в функцию f(x1, …, xn) вместо каждого аргумента xi либо константу ai, если i ≠ k, либо переменную x, если i = k (подстановка константы и переменной допустима по условию теоремы). В результате получим функцию одного аргумента
Итак, инверсия x получена. •
Пример. Рассмотрим функцию f(y,z) = y ↓ z.
Она немонотонна, так как существует пара наборов α=00 и β=10 таких, что α
Подтверждение
Пример я сам придумал, поэтому здесь, да, всё очевидно.
Но вот если в нём разделить вектор значений пополам и сравнивать 1101 и 1110, то несмотря на предшествование эти наборы не сравнимы.
Но вот если в нём разделить вектор значений пополам и сравнивать 1101 и 1110, то несмотря на предшествование эти наборы не сравнимы.
Ну вот!
Если они не сравнимы, значит функция немонотонна.
Т.е. несравнимость этих половинок означает, что на некоторых наборах значений переменных условие монотонности выполняется, а на некоторых нет.
Причем наборы значений переменных здесь попарно сравнимы.
Всё таки не до конца понятно, но тем не менее, уже ближе к цели.
mad-math, ну, задайте вопросы )
Я с удовольствием отвечу.
Давайте так. Вот таблица для вашей функции.
000 1
001 1
010 0
011 1
100 1
101 1
110 1
111 0
Что мы видим?
Во-первых, мы видим, что все взятые наборы переменных сравнимы и значит сравнение значений функции на них легитимно.
Во-вторых мы видим, что если бы функция была монотонна, то две половинки вектора значений были бы сравнимы. Потому что под номерами 1), 2), 3), 4) после точки с запятой как раз выполняется поэлементное сравнение первой и второй половин вектора f.
Сравнимость этих половинок необходимое, но не достаточное условие. Теперь нужно то же самое проделать для наборов значений переменных, отличающихся второй координатой и третьей.
Спасибо большое за желание помочь, просто мне неудобно напрягать людей.
Сейчас распишу мои размышления. Поправьте, если я где-то ошибаюсь.
Пусть есть функция `f(0001 0010)`.
Презентация по математике на тему «Монотонные булевы функции»
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
Монотонные булевы функции Авторы презентации: преподаватель математики ГПОУ ЯО ЯГК Холманова Вероника Михайловна M
Отношение предшествовать на B M По аналогии с отношением «меньше или равно» на рассмотрим отношение «предшествовать» на B
M Сравнимые элементы Bn Два элемента и называются сравнимыми между собой, если либо первый из них предшествует второму, либо второй предшествует первому, то есть: или Элементы (01) и (10) – несравнимые элементы B2
Класс монотонных булевых функций обозначается символом M. Булева функция n переменных называется монотонной, если для любых двух её аргументов, сравнимых между собой, из того, что первый предшествует второму следует, что значение функции на первом аргументе предшествует значению функции на втором аргументе: M Монотонные булевы функции
Проверку на монотонность удобно осуществлять для булевой функции, заданной таблицей значений. Если выполнены все условия определения, функция принадлежит классу монотонных булевых функций: Если найдутся любые два сравнимые между собой её аргумента, первый из которых будет предшествовать второму, а значение функции на первом аргументе не будет предшествовать значению функции на втором, то данному классу функция принадлежать не будет: Монотонные булевы функции M
Задача: исследовать функцию на принадлежность к классу монотонных булевых функций. Исследование булевой функции на монотонность M
0 0 1 1 0 1 1 0 1 1 0 0 Вектор задаёт булеву функцию двух переменных Исследование булевой функции на монотонность M
0 0 1 1 0 1 1 0 1 1 0 0 Исследование булевой функции на монотонность M
0 0 1 1 0 1 1 0 1 1 0 0 Исследование булевой функции на монотонность M
Отсутствие в булевом векторе после единиц нулей является достаточным условием монотонности булевой функции, заданной вектором Исследование булевой функции на монотонность M (по достаточному условию монотонности) f=(00000111),
Достаточное условие монотонности функции, заданной булевым вектором, не является необходимым. Исследование булевой функции на монотонность M f = (0 1 0 1) 0 0 1 1 0 1 1 0 1 1 0 0
Исследование булевой функции на монотонность M Если после единиц в булевом векторе присутствуют нули, функция нуждается в проверке на монотонность по определению Булева функция может быть как монотонной, так и немонотонной
Задача: исследовать функцию на принадлежность к классу монотонных булевых функций Исследование булевой функции на монотонность M
Зададим булеву функцию таблицей значений Исследование булевой функции на монотонность M 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 0 0 0 1 1 0 0 1 0 1 0 1 0 1 0 0 0 0 1 0 1 0 1 1 0 1 1 1 0 1 1 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0
Исследование булевой функции на монотонность M f=(01000100)
Исследование булевой функции на монотонность M 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 0 0 0 1 1 0 0 1 0 1 0 1 0 1 0 0 0 0 1 0 1 0 1 1 0 1 1 1 0 1 1 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 Второй и третий аргументы не сравнимы между собой
Исследование булевой функции на монотонность M 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 1 0 0 0 1 0 0
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-1596240
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Кабмин утвердил список вузов, в которых можно получить второе высшее образование бесплатно
Время чтения: 2 минуты
В Ульяновской области продлили школьные каникулы
Время чтения: 1 минута
«Спутник» объявили словом года в России
Время чтения: 2 минуты
Мишустин поручил проводить международную олимпиаду по философии
Время чтения: 0 минут
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
Прослушивание музыки снижает усталость мозга
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
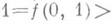
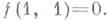
 Раздел 1. Математическая логика
Раздел 1. Математическая логика Тема 1. Логика высказываний
Тема 1. Логика высказываний