что такое тор в геометрии
ТОР (в геометрии)
Смотреть что такое «ТОР (в геометрии)» в других словарях:
ГЕОМЕТРИИ ОБЗОР — Геометрия раздел математики, тесно связанный с понятием пространства; в зависимости от форм описания этого понятия возникают различные виды геометрии. Предполагается, что читатель, приступая к чтению этой статьи, обладает некоторыми… … Энциклопедия Кольера
Тор (поверхность) — У этого термина существуют и другие значения, см. Тор. Красным образующая окружность Тор (тороид) поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в … Википедия
Кольца Юпитера — … Википедия
ЭЛЛИПТИЧЕСКАЯ КРИВАЯ — неособая полная алгебраическая кривая рода 1. Теория Э. к. является истоком большей части современной алгебраич. геометрии. Но исторически теория Э. к. возникла как часть анализа, как теория эллиптических интегралов и эллиптических функций.… … Математическая энциклопедия
АРИСТОТЕЛЬ — (Aristoteles) (384 322 до н.э.) великий др. греч. философ и ученый, создатель логики, основатель психологии, этики, политики, поэтики как самостоятельных наук. Родившись на северо востоке Греции (г. Стагира), провел 20 лет в Академии Платона (см … Философская энциклопедия
АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ — функция переменных x1. xn удовлетворяющая уравнению где F неприводимый многочлен от с коэффициентами из нек рого поля K, наз. полем констант. А. ф., заданная над этим полем, наз. А. ф. над полем K. Многочлен часто записывается по степеням… … Математическая энциклопедия
НЕДЕЗАРГОВА ГЕОМЕТРИЯ — геометрия на плоскости, в к рой Дезарга предложение может не иметь места. В этом случае плоскость наз. недезарговой плоскостью. Теорема Дезарга не может быть доказана в плоскости на основе лишь проективных аксиом плоскости без привлечения аксиом… … Математическая энциклопедия
РИМАНОВА ГЕОМЕТРИЯ В ЦЕЛОМ — раздел римановой геометрии, изучающий связи между локальными и глобальными характеристиками римановых многообразий (р. м.). Термин Р. г. в ц. обычно относят к определенному кругу проблем и методов, характерных для геометрии в целом. Основное… … Математическая энциклопедия
Эллиптическая кривая — Не следует путать с Эллипс. Эллиптическая кривая над полем K это множество точек проективной плоскости над K, удовлетворяющих уравнению вместе с точкой на бесконечности. Эллиптические кривые являются одним из основных объектов изучения в… … Википедия
Трехмерный мир, в котором мы не живем
Еще древние греки превратили математику из эмпирической науки в дедуктивную, потребовав вывода доказательств ее утверждений из основных понятий и исключив ссылку на опыт в качестве аргумента.
Чистая математика исследует формы и отношения в отвлечении от материального содержания. Ее непосредственным предметом оказываются, например, не те или иные тела шарообразной формы, а «идеальный шар», не те или иные совокупности предметов и даже не отдельные числа, а целые числа вообще и т. п.
Однако при всей абстрактности этой науки никто из математиков, по-видимому, не сомневался в том, что все их понятия, теоремы и формулы выражают реальные количественные и пространственные отношения. Математическая геометрия была теорией реального пространства, как позже механика явилась теорией движения
Математика — наука, изучающая
количественные и пространственные
формы и отношения действительности
Академик А. Д. Александров
Окружающий нас мир трехмерен. Мы привыкли к этой мысли с рождения — каждый человек знает, что такое высота, длина и ширина, три основных измерения окружающего нас пространства. В зависимости от традиций, принятых в разных странах, размеры предметов измеряют в метрах, футах, ли, лье и других эталонных единицах длины. Для наших дальнейших рассуждений выберем немного необычную единицу длины. Ею будет служить один световой год (1 св. г.), т. е. расстояние, проходимое лучом света за один календарный год. В традиционных мерах длины это составляет невообразимую величину — примерно 9,46•10 12 километров.
Если из окружающего нас пространства мысленно вырезать куб с ребром, равным 1 св. году, то внутри благополучно разместится дом, в котором мы живем, земной шар, Солнечная система… В общем, все, что необходимо для нормальной жизни человека. Для удобства назовем рассмотренный нами куб единичным кубом. А теперь отметим следующий очевидный факт. Несмотря на громадные размеры, наш единичный куб — лишь мельчайшая частица окружающего мира.
Кстати сказать, в этом определении размеры самого куба не задаются — вовсе не обязательно использовать кубы больших размеров. С таким же успехом можно утверждать, что каждая точка содержится в кубе, ребро которого не превосходит по длине, скажем, один микрон (10 —6 см).
Все сказанное выше кратко можно выразить следующими словами: окружающий нас мир является трехмерным евклидовым многообразием. А теперь попробуем ответить на следующий вопрос: как устроен мир за пределами единичного куба, в котором находится наш дом — наша Солнечная система?
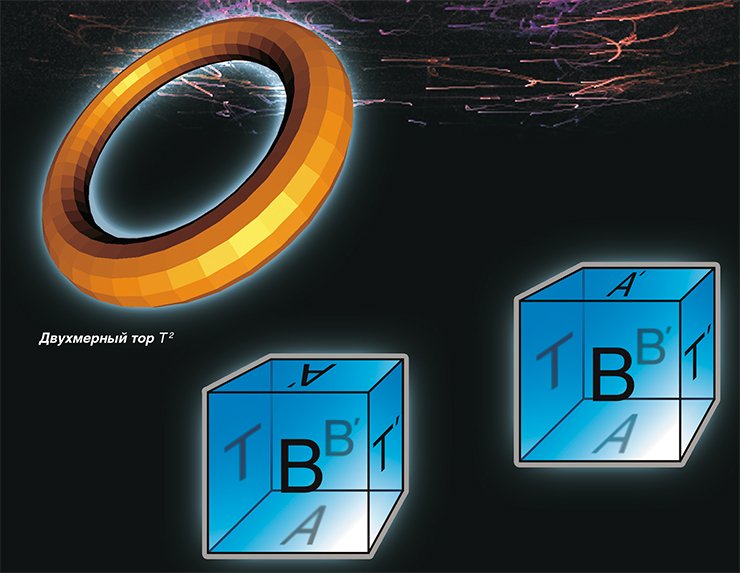
Трехмерный тор и другие
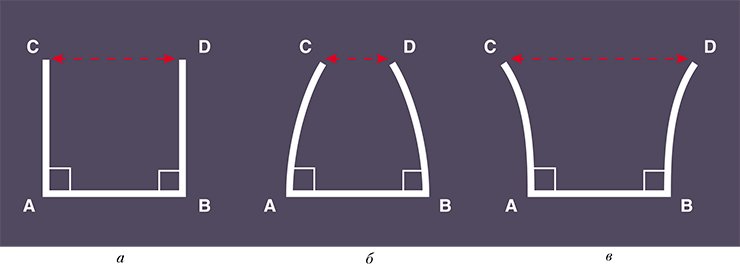
Если на минуту вообразить, что окружающее нас пространство бесконечно по всем направлениям, то ответ на вопрос о строении окружающего нас мира даст следующая теорема Адамара:
«Бесконечно протяженное по всем направлениям трехмерное евклидово многообразие М 3 совпадает с евклидовым пространством E 3 ».
Евклидово пространство Е 3 с прямоугольной системой координат всем хорошо известно, поэтому не будем подробно останавливаться на изучении его свойств.
Для того же, чтобы сделать наши рассуждения более содержательными и интересными, предположим другой вариант: окружающий нас мир замкнут, т. е. имеет конечные размеры и не имеет края. Другими словами, зададимся вопросом, как устроены замкнутые трехмерные евклидовы многообразия, или, другими словами, евклидовы формы. Полный ответ на этот вопрос дает теорема, доказанная Дж. Вольфом (1982):
Существует ровно десять трехмерных евклидовых форм. Причем шесть из них представляют собой ориентируемые, а остальные четыре — неориентируемые многообразия.
Все евклидовые формы строятся схожим образом, единственное — для построения некоторых из них нужно использовать куб, а для других — правильную шестиугольную призму.
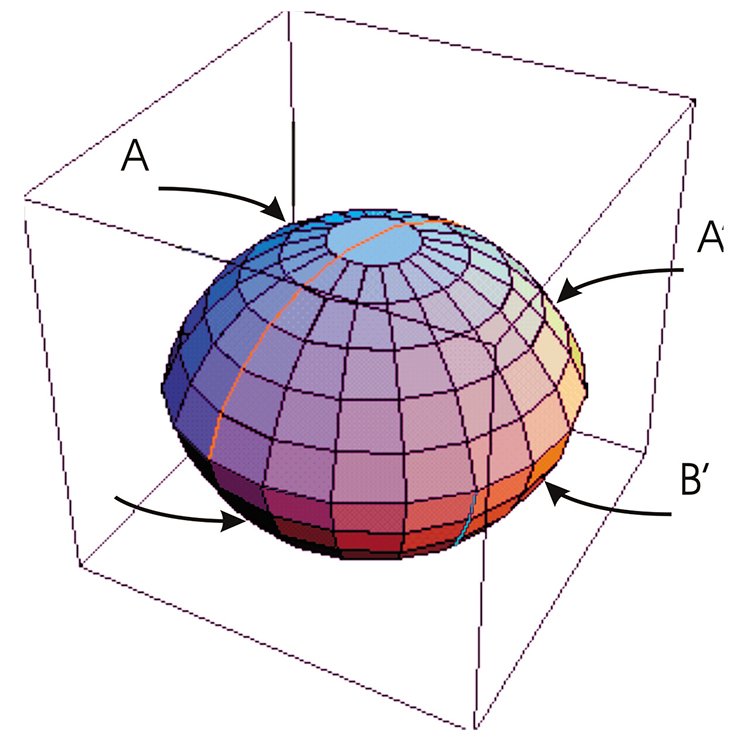
Для этого в центре грани А трехмерного тора поместим космический корабль, летящий со скоростью света, и заставим его стартовать в вертикальном направлении. Ровно через год космический корабль, продолжая двигаться по прямой, вернется в исходную точку. Теперь эта точка будет находиться в центре грани А’, которая, по условию, отождествлена с гранью А. В результате эксперимента обнаружим, что в трехмерном торе Т 3 существует замкнутая прямая линия l длиной в один световой год.
Поставим еще один аналогичный эксперимент. Заставим космический корабль стартовать из точки у, лежащей в грани А на расстоянии 1 км от ее центра. Через год корабль благополучно вернется в точку у. Вывод из второго эксперимента — через точку у проходит замкнутая прямая длиной 1 световой год, параллельная прямой l.
Многообразные многообразия
Как уже было замечено, все рассмотренные выше многообразия обладают евклидовой геометрией. Что это означает и какие еще геометрии существуют?
Наиболее известными и употребимыми в общечеловеческой практике являются евклидова, сферическая и гиперболическая геометрии. Напомним, что сферическую геометрию иногда называют геометрией Римана, а гиперболическую — геометрией Лобачевского. В трехмерном пространстве, кроме трех указанных, существует еще пять так называемых синтетических геометрий.
В соответствии с тем, какие геометрические законы действуют на трехмерном многообразии, будем называть его соответственно евклидовым, сферическим, гиперболическим или синтетическим.
Евклидовы многообразия мы уже рассмотрели выше. Что до остальных, то более двадцати лет назад У. Терстон (1978) доказал замечательную теорему: почти все трехмерные многообразия являются гиперболическими, то есть подчиняются законам геометрии Лобачевского. За этот результат в 1983 году он был удостоен Филдсовской премии — самой престижной награды для математиков.
Сферические многообразия бывают как трехмерные, так и многомерные (Вольф, 1982). В пространстве любой размерности существует конечное число типов таких многообразий. Синтетических многообразий очень мало (Thurston, 1978; Dunbar, 1981; Терстон, 2001) в отличие от оставшегося класса гиперболических многообразий. Последний неисчерпаемо широк и классификация его к настоящему времени не завершена.
Сферические многообразия
Все трехмерные сферические многообразия — ориентируемы. Это означает, что по какой бы замкнутой траектории не летал космический корабль с непрерывно вращающимся пропеллером, по возвращении в точку старта его пропеллер вращается в ту же сторону, что и в момент старта.
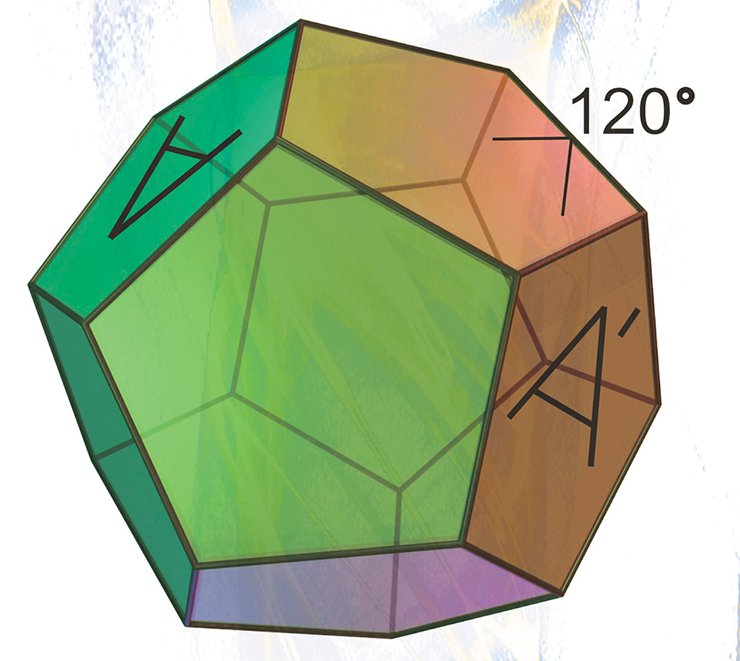
Третий, и пожалуй, самый нетривиальный пример сферического многообразия — сферическое пространство додекаэдра Пуанкаре или, для краткости, сфера Пуанкаре.
Сфера Пуанкаре удивительным образом связана с самыми различными разделами математики — геометрией, топологией, теорией групп, теорией катастроф, теорией узлов и другими (Кирби, Шарлеман, 1982).
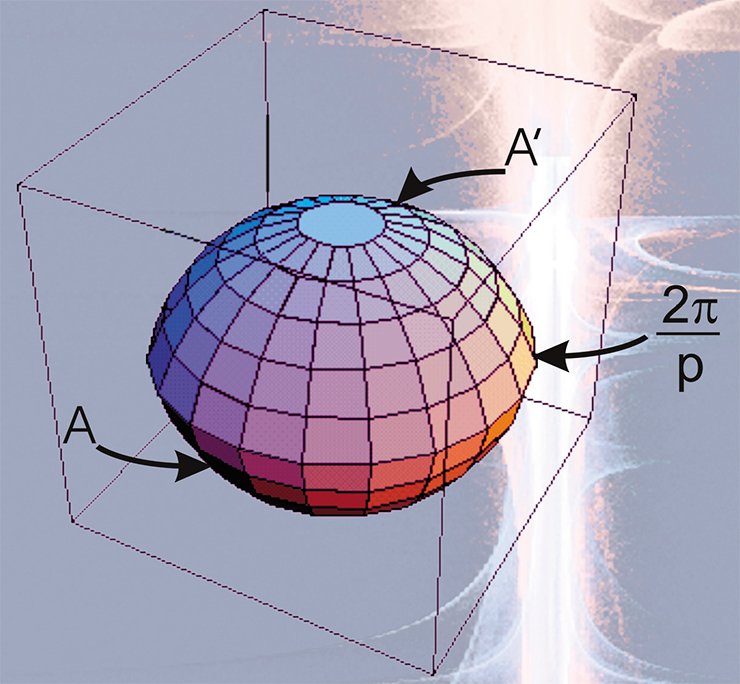
Все остальные сферические многообразия, получаемые по единой схеме, представляют собой так называемые линзовые и призматические пространства.
Гиперболические многообразия
Первое трехмерное замкнутое гиперболическое многообразие было построено немецким математиком Ф. Лебеллем в 1931 г. Однако построение его было достаточно сложным, поэтому двумя годами позже Х. Зейферт и К. Вебер предложили элегантную конструкцию гиперболического пространства додекаэдра.
С точки зрения математики наиболее сложная часть проблемы построения состоит в доказательстве существования этого гиперболического додекаэдра в пространстве Лобачевского. Положительный ответ на этот вопрос дает фундаментальная теорема Е. М. Андреева (1970), в которой сформулированы необходимые и достаточные условия для существования выпуклых гиперболических многогранников. Эта теорема служит одним из краеугольных камней современной теории гиперболических многообразий, созданной У. Терстоном.
Конструируем многообразия из многогранников
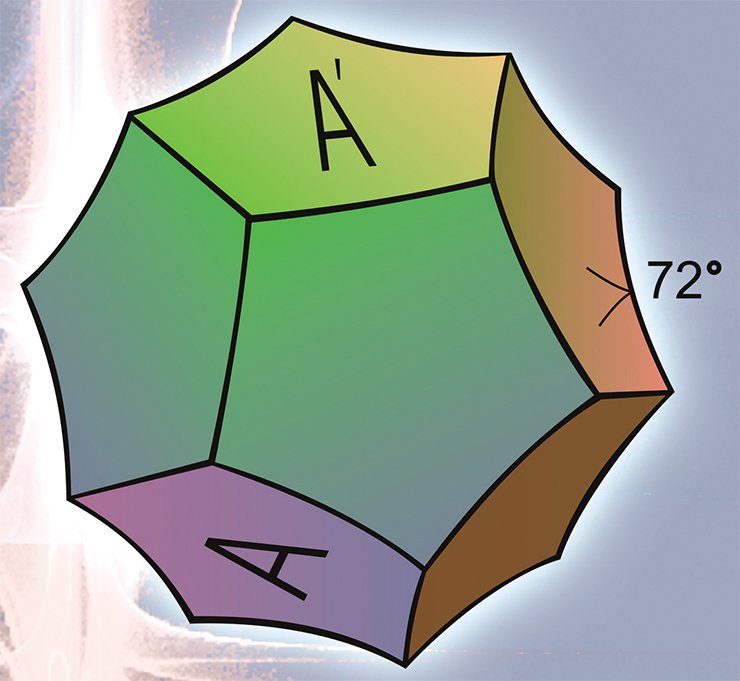
Рассмотрим прямоугольный многогранник Р, все двугранные (и плоские) углы которого равны 90°. В евклидовом пространстве в качестве такого многогранника можно взять куб, в сферическом — тетраэдр, а в гиперболическом — шестиугольную призму Лебелля, боковая поверхность которой состоит из 12-ти пятиугольников.
Из теоремы Андреева следует, что любой многогранник, у которого нет треугольных и четырехугольных граней, а в каждой вершине сходится ровно по три ребра, может быть реализован как прямоугольный многогранник в пространстве Лобачевского. Шестиугольная призма Лебелля, очевидно, удовлетворяет этим условиям.
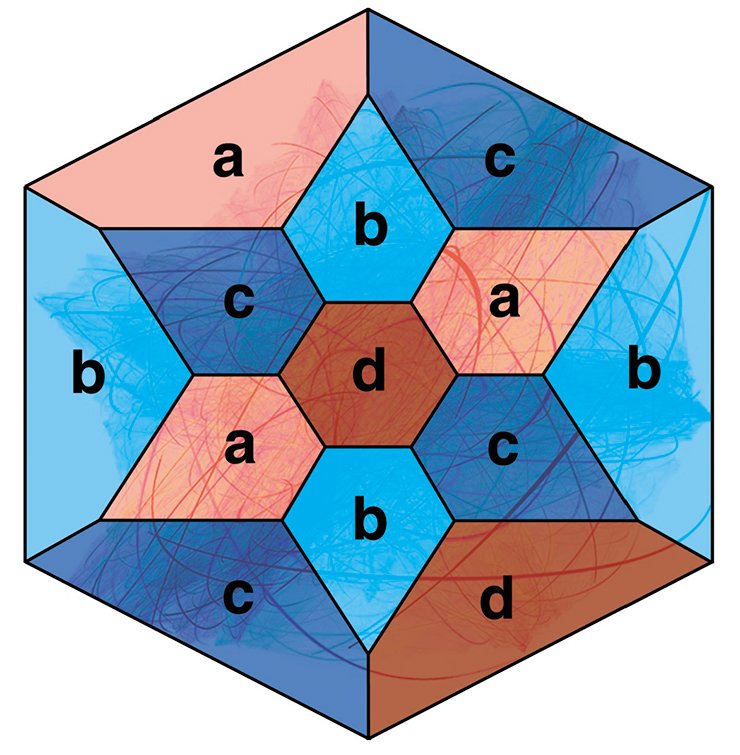
Для построения гиперболических многообразий используется способ, заключающийся в окраске смежных граней многогранника в разные цвета и последующего отождествления соответствующих граней, окрашенных в один цвет, у нескольких одинаковых экземпляров многогранников. Такой способ построения многообразий был впервые реализован Ф. Лебеллем (Loebell, 1931) для шестиугольной призмы, японским математиком М. Такахаши (Takahashi, 1985) — для правильного прямоугольного додекаэдра и А. Ю. Весниным (1987) — для произвольного прямоугольного многогранника Р.
При этом отметим, что все многообразия, построенные по окраске многогранника в четыре цвета, ориентируемы. Однако доказано, что окрашивая грани многогранника Р в пять, шесть или семь цветов, по аналогичной схеме можно построить и неориентируемые многообразия (Mednykh, 1992).
Остановимся еще на одном свойстве прямоугольных многогранников. Пусть D — правильный прямоугольный додекаэдр в пространстве Лобачевского. Испанский математик Х.-М. Монтезинос (Hilden et al., 1987) доказал следующую замечательную теорему:
«Любое замкнутое трехмерное многообразие может быть получено из конечного числа экземпляров многогранника D попарным отождествлением их граней».
Отметим, что в теореме Монтезиноса все грани склеенных многогранников — конгруэнтны, а все ребра имеют одинаковую длину. При этом каждое ребро окружено четырьмя, двумя или одним додекаэдром. Первую ситуацию легко представить: четыре прямоугольных додекаэдра склеены друг за другом вокруг общего ребра и образуют суммарный угол, равный 4•90° = 360°. Во втором случае пара смежных граней одного додекаэдра отождествляется с парой смежных граней другого додекаэдра. Суммарный двугранный угол вокруг ребра, принадлежащего двум додекаэдрам, в этом случае равен 2•90° = 180°. Третий вариант легко создать, отождествляя смежные грани одного додекаэдра поворотом на угол 90°.
Наличие ребер второго и третьего типа превращает многообразие в многообразие с особенностями, или орбифолд. В этом случае указанные ребра образуют сингулярное множество орбифолда. Заметим, что всюду, кроме сингулярных ребер, многообразие обладает геометрией Лобачевского.
Трехмерные орбифолды
Евклидовы орбифолды
Для всякого трехмерного евклидова орбифолда существует фундаментальное множество — криволинейный многогранник, из которого заданный орбифолд можно получить, попарно отождествляя (склеивая) определенные его грани.
Примерами евклидовых орбифолдов могут служить так называемые Борромеевы кольца или трехмерная сфера с сингулярным множеством узел «восьмерка».
Всего существует 230 замкнутых трехмерных евклидовых орбифолдов — по числу кристаллографических групп, открытых в конце прошлого века русским ученым Е. С. Федоровым. Строение евклидовых орбифолдов было полностью описано в докторской диссертации У. Данбара, защищенной в 1981 г. в Принстонском университете — крупнейшем математическом центре мира.
Сферические орбифолды
Сингулярным множеством сферических орбифолдов может служить так называемый рациональный узел или зацепление. Им может оказаться также заузленный граф, из каждой вершины которого выходит по три ребра. В частности, сингулярным множеством сферического орбифолда будет являться скелет тетраэдра (ребра + вершины), расположенный в трехмерной сфере.
q > l. В сферическом пространстве S ³ рассмотрим линзу с углом, равным π/р и поделим ее ребро точками 1,2. 2р на 2р равных частей. Соединим пары точек <р, 2р>и
При этом следует иметь ввиду, что сильные заузливания тетраэдра могут испортить сферическую геометрию и заставить орбифолд обладать евклидовой, гиперболической или одной из синтетических геометрий.
Недавно австралийцами профессором К. Ходжсоном и его учеником Д. Хеардом создана компьютерная программа, позволяющая вычислять объемы заузленных графов, вложенных в трехмерную сферу (Hodgson and Heard, 2005). Полная классификация трехмерных орбифолдов во всех геометриях, кроме гиперболической, сделана в работах У. Данбара. Как и в случае многообразий, гиперболическая геометрия является наиболее богатой, и полное описание орбифолдов в ней до сих пор не получено.
Гиперболические орбифолды
Из теоремы Монтезиноса следует, что каждое трехмерное многообразие может быть превращено в гиперболический орбифолд, если внутрь его поместить подходящее сингулярное множество. Поскольку существует бесконечно много различных многообразий, отсюда следует, что существует также бесконечно много гиперболических орбифолдов.
Один из простейших гиперболических орбифолдов — трехмерная сфера с сингулярным множеством Борромеевы кольца с индексом сингулярности 4. Другой пример — сильно заузленный тетраэдр, все ребра которого имеют индекс сингулярности два. Доказательство таких фактов обычно достаточно сложно и может быть проведено с помощью теорем о геометризации, полученных У. Терстоном, его учениками и последователями. Общий принцип доказательства состоит в следующем: если орбифолд не является евклидовым, сферическим или синтетическим и удовлетворяет некоторым простым геометрическим условиям, то он — гиперболический.
Изменения, произошедшие в математике за последние более чем полтора века, не только необозримо расширили ее содержание, но и изменили его принципиально. В предмет математики сейчас входит любая структура, которую можно исследовать путем логического рассуждения с достаточной строгостью и богатством выводов. Найдет ли она применение и прообраз в действительности — это уже вопрос не к математике.
Понятно, что фактически наибольшее развитие получают те теории, которые находят существенные применения в самой математике и тем более за ее пределами. Хотя опыт развития науки уже достаточное число раз показал, как самые отвлеченные теории находили потом чрезвычайно существенные приложения. Но для самой чистой математики это в принципе безразлично. Лучше всего творческое кредо новой математики выразил создатель теории множеств Г. Кантор, гордо зявив: «Сущность математики. в ее свободе».
Винберг Э. Б. О неевлидовой геометрии, Соросовский образовательный журнал, № 3, 1996, С. 104—109.
Тёрстон У. Трехмерная геометрия и топология, М: МЦНМО, 2001 (Перевод с англ. под ред. О. В. Шварцмана).
Hodgson C., Heard D. Computer program “Orb”, August 2005, http://www.ms.unimelb.edu.au/
Работа поддержана грантом РФФИ (№ 06-01-00153) и INTAS (№ 03-01-3663)
Автор и редакция выражает искреннюю благодарность Н. В. Абросимову (вед. инженеру Института математики им. С. Л. Соболева СО РАН, студенту 6-го курса НГУ), оказавшему неоценимую помощь при подготовке публикации
Что такое тор в геометрии
Пример тора можно построить, взяв прямоугольную полоску гибкого материала, например, резиновый лист, и соединив верхний край с нижним краем, а левый край с правым краем без каких-либо полувручений (ср. Лента Мебиуса ).
\ theta, \ varphi & = [0,2 \ пи) \ конец <выровнено>>> 
Три класса стандартных торов соответствуют трем возможным соотношениям сторон между R и r :
Поскольку тор имеет две центральные точки, центральные точки углов перемещаются; φ измеряет тот же угол, что и в сферической системе, но известен как «тороидальное» направление. Центральная точка θ перемещается в центр r и известна как «полоидальное» направление. Эти термины были впервые использованы при обсуждении магнитного поля Земли, где «полоидальное» использовалось для обозначения «направления к полюсам». [5]
Тор также может быть описан как фактор в декартовой плоскости под идентификаций
Фундаментальная группа тора является только прямым произведением фундаментальной группы окружности с самим собой:
Интуитивно говоря, это означает, что замкнутый путь, который огибает «дыру» тора (скажем, круг, обозначающий определенную широту), а затем обходит «тело» тора (скажем, круг, проводящий определенную долготу) можно деформировать до траектории, огибающей тело, а затем отверстие. Таким образом, коммутируют строго «широтные» и строго «продольные» пути. Эквивалентное утверждение можно представить как два шнурка, проходящие друг через друга, затем разматывающиеся, а затем перематывающиеся.
Если проколоть тор и вывернуть его наизнанку, то получится другой тор, в котором линии широты и долготы поменяются местами. Это эквивалентно созданию тора из цилиндра путем соединения круглых концов вместе двумя способами: снаружи, как соединение двух концов садового шланга, или через внутреннюю часть, как скручивание носка (с отрезанным носком). Кроме того, если цилиндр был создан путем склеивания двух противоположных сторон прямоугольника, выбор двух других сторон вместо этого вызовет такое же изменение ориентации.
Первая группа гомологий тора изоморфна фундаментальной группе (это следует из теоремы Гуревича, поскольку фундаментальная группа абелева ).
Пространство конфигурации
Простое 4-мерное евклидово вложение прямоугольного плоского тора (более общего, чем квадратный) выглядит следующим образом:
 род два |  род три |
Термин «тороидальный многогранник» также используется для многогранников высшего рода и для погружений тороидальных многогранников.
Таким образом, короткая точная последовательность группы классов отображений расщепляется (идентификация тора как фактора R n дает расщепление посредством линейных отображений, как указано выше):
Группа классов отображения поверхностей высшего рода намного сложнее и является областью активных исследований.