что такое тетрада в информатике
Значение слова «тетрада»
Тетрада — бивалент или тетрада гомологичных хромосом.
Тетрада (образование пыльцы) — группа из четырёх гаплоидных незрелых пыльцевых зёрен, образовавшихся в результате мейотического деления в ходе микроспорогенеза.
Тетрада (генетика) — группа из четырёх гаплоидных спор, образовавшихся после рекомбинации у некоторых грибов, например, нейроспоры и дрожжей.
Тетрада в информатике — шестнадцатиричный разряд, равный четырём битам или половине байта.
Тетрада (астрономия) — четыре подряд лунных затмения
тетра́да
1. книжн. единство, образуемое четырьмя предметами, понятиями или частями, членами
2. биол. группа из четырёх гаплоидных незрелых пыльцевых зёрен, образовавшихся в результате мейотического деления в ходе микроспорогенеза
3. биол. группа из четырёх гаплоидных спор, образовавшихся после рекомбинации у некоторых грибов, например, нейроспоры и дрожжей
4. астрон. четыре затмения подряд
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: самоуспокоенность — это что-то нейтральное, положительное или отрицательное?
Перевод из одной системы счисления в другую с помощью триад и тетрад
Развивающая – развивать познавательный интерес учащихся, умения применять полученные знания на практике.
Воспитательная – повысить уровень информационной культуры учащихся.
I. Проверка домашнего задания
Вызывается ученик к доске для выполнения домашнего упражнения
II. Изучение нового материала
Так как основания 8-1 и 16-й СС являются степенями двойки, то перевод чисел из этих СС в 2-ую и наоборот прост и основан на методах триад и тетрад. Число делится на триады (тетрады) вправо и влево от десятичной точки. Если крайние триады (тетрады) оказались неполными, они дополняются нулями.
| Алфавит | Триады | Тетрады |
| 0 | 000 | 0000 |
| 1 | 001 | 0001 |
| 2 | 010 | 0010 |
| 3 | 011 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | |
| 9 | 1001 | |
| А(10) | 1010 | |
| В(11) | 1011 | |
| С(12) | 1100 | |
| D(13) | 1101 | |
| E(14) | 1110 | |
| F(15) | 1111 |
Упражнение: Выполнить перевод, используя тетрады и триады:
IV. Самостоятельная работа
Выполнить перевод, используя тетрады и триады:
Использование таблицы треад и тетрад
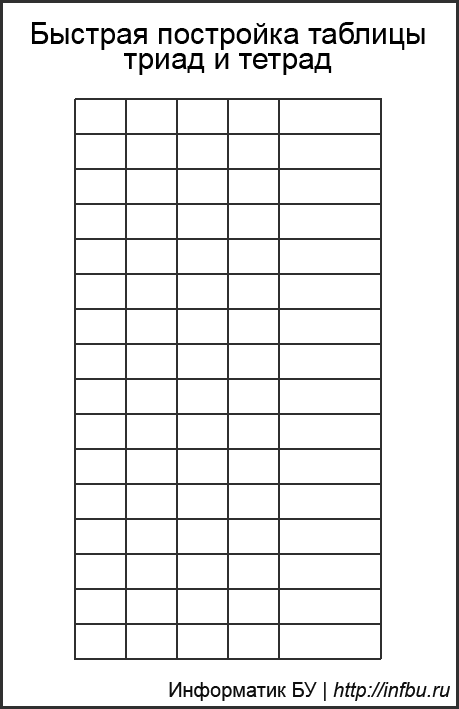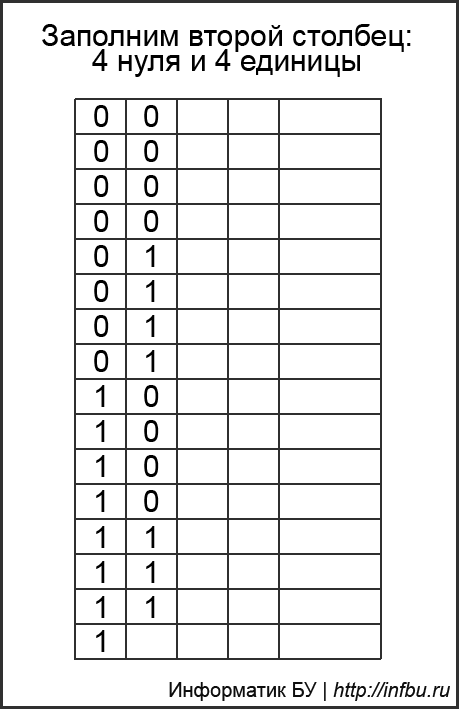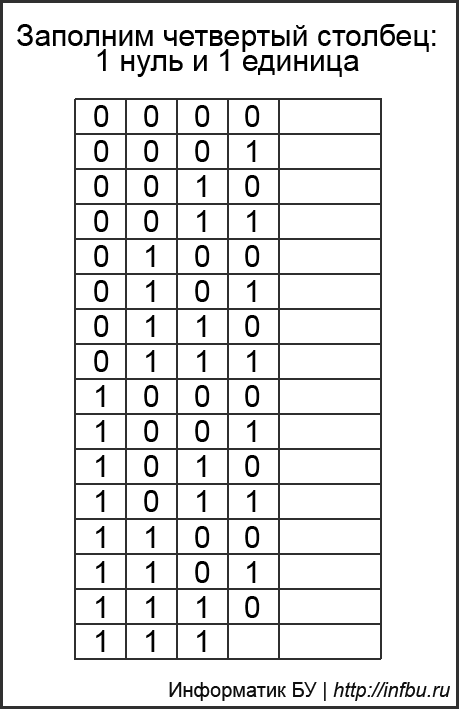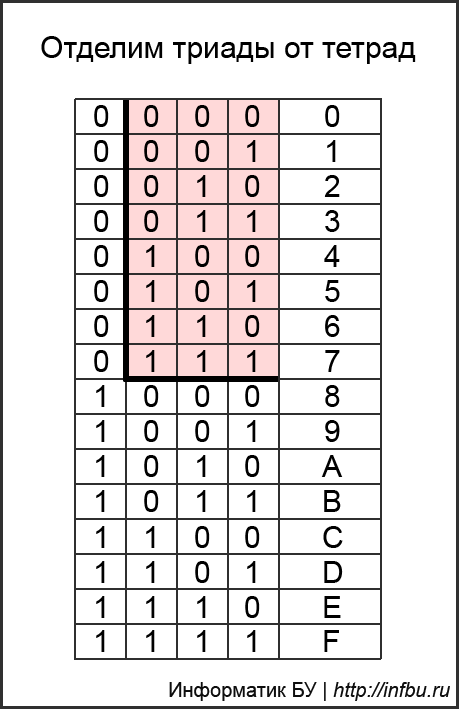
Таблицу триад и тетрад вы можете увидеть, щелкнув по кнопке в правом нижнем углу сайта. Она нужна для быстрого перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную и наоборот.
Многие зазубривают таблицу, но она строится очень просто без зубрёжки:
Перевод чисел из восьмеричной системы счисления в двоичную
Возьмем восьмеричное число 34568
Представим каждый разряд числа в виде триады:
Избавимся от первого незначащего нуля и получим результат:
Перевод чисел из двоичной системы счисления в восьмеричную
Возьмем число 111011012
Разделим его на триады, начиная с правого разряда:
Добавим один незначащий нуль:
Заменим триады значениями из таблицы:
Получается, что 3558 = 111011012
Перевод чисел из шестнадцатеричной системы счисления в двоичную
Возьмем число 15F16
Представим каждый разряд в виде тетрады:
Избавимся от трех первых незначащих нулей и запишем результат:
Получается, что 1010111112 = 15F16
Перевод чисел из двоичной системы счисления в шестнадцатеричную
Возьмем число 100010110111012
Разделим его на тетрады, начиная с правого разряда:
0010 0010 1101 1101
Заменим тетрады значениями из таблицы:
Получается, что 22DD16 = 100010110111012
Интерфейс ADM – что такое «Тетрада»
Интерфейс ADM это внутренний стандарт компании «Инструментальные Системы». Он определяет правила соединения субмодулей ADM и базовых модулей. Ключевым элементом интерфейса является ПЛИС ADM. Изначально использовались ПЛИС серий FLEX10K и Acex 1K фирмы Altera. В 2003 году начался переход на ПЛИС Xilinx. Используются практически все серии ПЛИС от Spartan 2E до Kintex Ultrascale. Базовым элементом проекта ПЛИС является «тетрада». Данная статья именно об этом.
Базовый вариант интерфейса ADM на основе ПЛИС Altera получил название «Интерфейс ADM. Классическая реализация». Его особенностью является наличие в ПЛИС блока из шестнадцати регистров. Часть регистров обслуживала FIFO, часть регистров отводилась на обслуживание субмодуля. С ростом сложности изделий шестнадцати регистров стало недостаточно для организации управления. Ситуация осложняется тем, что на многих базовых модулях к ПЛИС подключены только пять или шесть адресных линий, на большее просто не хватает ножек. В такой ситуации логичным решением является организация косвенной адресации, но при этом требуется оставить быстрый доступ к регистрам FIFO. В результате появилась новая реализация, которая получила название «Интерфейс АDM. Прогрессивная реализация».
Логическая реализация
Основным элементом является тетрада. Тетрада это логический объект, который имеет четыре прямо адресуемых регистра и 1024 косвенно адресуемых регистра.
Логическая организация тетрады представлена на рисунке:
Группа констант сохраняет наиболее важную информацию о тетраде. В первую очередь это идентификатор тетрады, номер версии а также наличие и направление работы FIFO. Идентификатор тетрады однозначно определяет набор регистров.
Непосредственные регистры позволяют реализовать регистры с любым поведением, в том числе дополнительные регистры состояния. При этом следует помнить, что реализация регистров на чтение потребует реализации мультиплексора, который является пожирателем ресурсов ПЛИС. Рекомендуется наибольшее число регистров помещать в группу командных и по минимуму – в группу непосредственных.
В настоящее время для организации теневого ОЗУ всех тетрад используется только один блок памяти ПЛИС. Это позволяет организовать в каждой тетраде 32 командных регистра и 32 константы. В любой момент это количество можно увеличить, но пока этого не потребовалось.
В прошивке ПЛИС может быть шестнадцать тетрад. Каждая тетрада управляет своей какой-либо законченной частью интерфейса.
Для примера приведён состав тетрад для прошивки модуля FMC107P и субмодуля FM216x250MDA
Реализация на VHDL
Проект ПЛИС написан на языке VHDL. Для подключения тетрады используются специальные типы данных, что резко уменьшает объём текста. В настоящее время существует три типа подключения. В первую очередь они отличаются шириной шины данных, а во вторую – типом сигналов подключения.
Тип 1 – ширина шины данных 64 бита. Используются с сигнальными процессорами и интерфейсом PCI Express v1.1 x8
Тип 2 – ширина шины данных 128 бит. Используются с интерфейсом PCI Express v2.0 x8
Тип 3 – ширина шины данных 512 бит. Используется с интерфейсом PCI Express v3.0 x16
Во всех случаях тактовая частоты шины до 266 МГц. Если не требуется максимальное быстродействие, то рекомендуется снижать тактовую частоту для облегчения трассировки ПЛИС.
Базовым типом данных является тип bl_cmd
Существует отдельный тип для описания сигнала запроса DMA
Описание тетрады типа 1 выглядит так:
За исключением сигналов тактовой частоты и сброса используется шесть сигналов.
Для тетрады типа 2 число сигналов уменьшилось до двух.
С ростом объёма ПЛИС увеличиваются трудности при размещении компонентов тетрад внутри ПЛИС. Это связано с высокой тактовой частотой и большой длиной соединений.
При этом высокая тактовая частота нужна только для передачи данных. Для обращения к регистрам достаточно 100 МГц. Типы подключения 1 и 2 используют только один сигнал тактовой частоты. Для типа 3 используется две тактовые частоты и дополнительный компонент repack. Компонент repack установлен между тетрадой и узлом подключения к шине. Он имеет параметр STAGE, который определяет количество дополнительных триггеров в шине данных. Кроме того, возможна реализация нескольких модификаций для подключения тетрад типа 1 и 2. На рисунке представлена конфигурация в которой через компонент REPACK_128 подключена тетрада типа 2 и через компонент REPACK_512 подключена тетрада типа 3, при этом используется параметр STAGE=4 который позволяет установить тетраду в любом месте ПЛИС Virtex 7.

В заключение хотелось бы отметить что тетрады оказались очень удобными для модульного построения прошивок ПЛИС и модульного построения программного обеспечения. Концепция тетрад активно используется более 12 лет. Тетрады пережили рост ПЛИС и изменение серий от Spartan 2E до Virtex 7 и внедряются в серию Ultrascale. Скорость ввода поднялась от 200 Мбайт/с до 11 Гбайт/с. Поддержано большое количество субмодулей. Произошёл переход от внутрифирменного стандарта ADM к международному стандарту FMC.
Более подробное описание тетрад приведено в документе: «DCR0340 – Интерфейс ADM. Прогрессивная реализация». В соответствии с правилами Habrahabr, ссылку на документ дать не могу.
Что такое тетрада в информатике
Любой вид информации можно представить в виде чисел. Кодирование информации с помощью чисел осуществляется по определённым правилам. Для понимания этих правил, разберём логику образования любого числа.
| Система счисления – это правила записи чисел с помощью знаков – цифр и операций над ними.
Любое число, в данной системе счисления, образуется путём повторения одинаковых элементов (палочка, камешек, ракушка и т.д.).
Данная система счисления позволяет записывать только натуральные числа и запись «большого» числа получается очень громоздкой.
В дальнейшем, у человечества возникла необходимость производить серьёзные подсчёты. Для этого были придуманы непозиционные системы счисления.
| Непозиционная система счисления – это система счисления, в которой цифра не изменяет своего значения, от изменения позиции в числе.
Египетская система счисления 
Кириллическая система счисления 
Римская система счисления 
| Позиционная система счисления – это система счисления, в которой цифра изменяет своё значения, при изменении позиции в числе.
Вспомним, что любое число в десятичной (арабской) системе счисления можно разложить на разряды. Например, в числе 753 цифра 7 обозначает сотни (700), цифра 5 – десятки (50), цифра 3 – единицы. Таким образом, число можно представить, как:
753 = 7 * 100 + 5 * 10 + 3 * 1
| Алфавит системы счисления – совокупность всех её цифр.
| Основание системы счисления – указывает на количество цифр в данной системе счисления.
Алфавит десятичной системы счисления состоит из цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Следовательно, основанием данной системы счисления является 10.
Тогда, любое число будем записывать по правилу, с указанием основания данной системы счисления:
Число читается, как «семьсот пятьдесят три по основанию десять» или «семьсот пятьдесят три в десятичной системе счисления».
| Разряд – это позиция цифры в числе (нумерация в целых числах производится с права налево, начиная с нуля).
Укажем разряд каждой цифры в числе 753:
Развёрнутая форма представления чисел
В результате разбиения числа на разряды, любое такое число можно представить в развёрнутой форме.
Формула развёрнутой формы представления чисел:
q – основание системы счисления;
a – цифра данного числа;
n – число разрядов в числе.
Представим число 75310 в развёрнутой форме.
1) Определим позиции каждой цифры в числе:
Каждую цифру в числе, умножим в соответствии занимаемой позицией:
Для упрощения данной записи, представим данное число, как основание 10 в степени n:
Запишем полученный результат.
Обратите внимание, что степень основания числа совпадает с позицией каждой цифры в числе!
Перевод числа в десятичную систему счисления
С помощью развёрнутой формы представления чисел можно перевести число из любой системы счисления в десятичную.
✒ Определение: каждую цифру числа нужно умножить на его основание, возведённое в степень, равную позиции цифры в числе.
Двоичная система счисления
Алфавит системы счисления: 0, 1.
Перевод десятичного числа в двоичную систему счисления методом подбора степеней числа 2
Для перевода двоичных чисел в десятичную систему счисления, используют метод подбора степеней двойки.
Пусть дано десятичное число 2110.
1) Подберём ближайшую наименьшую степень числа 2 к данному числу: 2 4 = 16;
3) Повторить, пока не достигнем нуля.
В результате, мы получим следующие степени:
Найденные нами степени – это позиции цифры 1 в двоичном числе, а отсутствующие степени – это нули:
Перевод целого десятичного числа в другую систему счисления методом деления на новое основание
✒ Определение: Для перевода целого десятичного числа в другую систему счисления, необходимо делить данное число на новое основание (той системы счисления, в которую необходимо осуществить перевод). Ответ складывается из остатков от деления.
Переведите число 1310 в двоичную систему счисления.
Перевод целого десятичного числа в другую систему счисления методом деления на новое основание
✒ Определение: Для перевода целого десятичного числа в другую систему счисления, необходимо делить данное число на новое основание (той системы счисления, в которую необходимо осуществить перевод). Ответ складывается из остатков от деления.
Переведите число 9710 в четверичную систему счисления.
Перевод методом триад и тетрад
✒ Определение: Для перевода числа из двоичной системы счисления в восьмеричную, его необходимо разбить на триады. Если не хватает цифр до полной триады, её дополняют незначащими нулями.
Число 11001001102 перевести в восьмеричную систему счисления.
| Незначащий нуль – это нули перед или после числа, дополнение которыми никак не изменяет значение самого числа.
Дополним число 112 до триады:
Дополним число 11,012 до двух триад:
✒ Определение: Для перевода числа из двоичной системы счисления в шестнадцатеричную, его необходимо разбить на тетрады. Если не хватает цифр до полной тетрады, её дополняют незначащими нулями.
Число 11001011002 перевести в шестнадцатеричную систему счисления.
Непозиционные системы счисления
1. Вычислите десятичное число, записанное в римской системе счисления:
| а) XVII | д) DCCCXLVI | з) DCCXCV |
| б) LXXII | е) CCXLVIII | к) CCCLXXII |
| в) CXXIX | ж) DXCIX | л) DCCLXXVII |
| г) XCIX | з) DCCXCV | м) MMCMXCIX |
2. Представьте данное десятичное число в римской системе счисления:
| а) 42 | д) 426 | з) 925 |
| б) 76 | е) 267 | к) 2019 |
| в) 132 | ж) 142 | л) 1744 |
| г) 198 | з) 530 | м) 3333 |
Позиционные системы счисления
3. Определите вес (позицию) цифры 3 в числе 8736.
4. Определите вес (позицию) цифры 4 в числе 4865.
5. Определите вес (позицию) цифры 2 в числе 112358.
6. Определите вес (позицию) цифры 9 в числе 9631.
7. Определите вес (позицию) цифры 5 в числе 835776.
8. Укажите название системы счисления, алфавит которой состоит из следующих цифр: 0; 1.
9. Укажите название системы счисления, алфавит которой состоит из следующих цифр: 0; 1; 2; 3.
10. Укажите название системы счисления, алфавит которой состоит из следующих цифр: 0; 1; 2; 3; 4; 5; 6; 7.
11. Укажите название системы счисления, алфавит которой состоит из следующих цифр: 0; 1; 2; 3; 4.
12. Укажите название системы счисления, алфавит которой состоит из следующих цифр: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; А; В.
13. Некоторое число представлено в развёрнутой форме. Запишите это число в свёрнутой форме представления и укажите основание системы счисления, в которой записано это число:
14. Запишите число в развёрнутой форме представления:
Переводы методом развёрнутой формы представления
15. Выполните перевод чисел из двоичной системы счисления в десятичную систему методом развёрнутой формы представления числа:
| а) 1100 | д) 1100011 | з) 1001110111000 |
| б) 11000 | е) 100101101 | к) 1001000010111 |
| в) 101010 | ж) 101110110 | л) 101110101111 |
| г) 1100011 | з) 111111 | м) 1111111 |
16. Даны числа в различных системах счисления. Выполните перевод в десятичную систему методом развёрнутой формы представления числа:
17. Выполните перевод из десятичной системы счисления в двоичную методом подбора степеней числа 2:
| а) 42 | д) 232 | з) 400 |
| б) 97 | е) 286 | к) 405 |
| в) 111 | ж) 309 | л) 528 |
18. Выполните перевод из десятичной системы счисления в двоичную методом деления на новое основание:
| а) 20 | д) 100 | з) 568 |
| б) 31 | е) 102 | к) 443 |
| в) 49 | ж) 127 | л) 500 |
| г) 96 | з) 269 | м) 600 |
19. Сравните числа, записанные в двоичной системе счисления:
20. Выполните перевод из десятичной системы счисления в восьмеричную методом деления на новое основание:
| а) 29 | д) 189 | з) 247 |
| б) 46 | е) 154 | к) 549 |
| в) 99 | ж) 177 | л) 627 |
| г) 110 | з) 133 | м) 633 |
21. Выполните перевод из десятичной системы счисления в шестнадцатеричную методом деления на новое основание:
| а) 118 | д) 248 | з) 511 |
| б) 126 | е) 216 | к) 918 |
| в) 149 | ж) 299 | л) 1200 |
| г) 113 | з) 303 | м) 1346 |
22. Выполните перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную методом разбиения числа на триады и тетрады: