что такое событие в математике
События, виды событий
Опыт, эксперимент, наблюдение явления или некоторого процесса называется испытанием. Примеры испытаний: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесённой на каждую из шести граней цифры от одного до шести), реализация некоторого физического, механического или технологического процесса и т.д. При бросании монеты исходами (событиями) являются выпадение герба или выпадение цифры, а при бросании игральной кости — выпадение какой либо цифры на верхней грани кости. Испытания сопровождаются их исходами (событиями).
Событие — это качественный и (или) количественный результат испытания (исход), осуществляемого при определённой совокупности условий. Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д.
Различают следующие типы событий: случайные события, совместные или несовместные события, достоверные или невозможные события, зависимые или независимые события, равновозможные события, элементарные (простые, неразложимые) события, событие или совокупность событий (исходов), благоприятствующих какому-либо другому событию.
Случайное событие – это результат испытания (или величина), который нельзя заранее спрогнозировать, т.е. нельзя сказать, произойдёт это событие или не произойдёт, или, если событие произойдёт, то неизвестно, какое значение примет результат этого события.
Случайные события – первичные, неопределяемые (в строгом смысле) понятия в теории вероятностей, аналогичные понятиям точки и прямой – в геометрии.
Например, пусть игральная кость с пронумерованными гранями от 1 до 6 подбрасывается два раза. В этом опыте можно рассматривать следующие события: событие А – оба раза выпадет число 1; событие В – хотя бы один раз выпадет число 3; событие С – сумма выпавших чисел равна 8 и т.д.
Событие, которое обязательно наступит (никогда не произойдёт) в данном опыте, называется достоверным (невозможным). Достоверное событие обозначают символом Ω, а невозможное – Æ. Например, в опыте, состоящем в подбрасывании кости один раз – событие А – выпадение одного из чисел 1,2,3,4,5,6 – есть достоверное, а событие В – выпадение числа 7 – невозможное.
Два случайных события называются несовместными, если наступление одного из них исключает наступление другого в одном и том же испытании. (Таким образом, несовместные события не могут наступать одновременно). В противном случае, т.е. если наступление одного события не исключает наступление другого события в одном и том же испытании, то эти события называются совместными. Например, если событие А – появление числа 2 при одном бросании кости, а событие В – появление чётного числа в этом же бросании, то события А и В совместные, а событие С – появление числа 2 при одном бросании кости и событие D – появление числа 3 в этом бросании – события несовместные.
События называются равновозможными, если ни одно из них не является более возможным по сравнению с другими событиями.
События называются независимыми (зависимыми), если числовая характеристика возможности наступления одного события не зависит (зависит) от числовых характеристик наступления других событий (указанные числовые характеристики некоторых событий А, В, С, … называются вероятностями этих событий).
Определение. Совокупность попарно несовместных событий образуют полную группу событий для данного испытания, если в результате каждого испытания происходит одно и только одно из них.
Примеры полных групп событий: а) выпадение герба <Г>и выпадение цифры <Ц>при одном бросании монеты; б) попадание в цель и промах при одном выстреле по мишени; в) выпадение цифр «1», «2», «3», «4», «5», «6» при одном бросании кости.
Множество всех элементарных событий называется пространством элементарных событий и обозначается Ω. Например, в результате бросания кости выпадение цифры i = 1, 2, 3, 4, 5, 6 образует пространство Ω = <1, 2, 3, 4, 5, 6>.
Элементарные события, составляющие пространство Ω, обозначаются ω1, ω2, …, ω6.
Замечание. Кроме случайных событий в теории вероятностей вводятся в рассмотрение случайные величины. Случайная величина – это переменная, которая в результате испытания в зависимости от случая принимает одно из возможных значений. Случайные величины в данном пособии рассматриваются более подробно в главе 3.
Лекция «События.Виды событий.Комбинации событий!
Все, что происходит или не происходит в реальной действительности, называют явлениями или событиями. Если некоторое событие происходит довольно часто, то в его наступлении существует определенная закономерность. Раздел математики, изучающий закономерности массовых явлений называется теорией вероятностей.
1) Событие, которое в некотором испытании может произойти, а может и не произойти, называют случайным событием.
2) Событие, которое в данном испытании обязательно произойдет, называют достоверным событием.
3) Событие, которое в данном испытании наступить не может, называют невозможным событием.
Играющий бросает кубик и смотрит, какое число выпало на грани, которая располагается сверху. Какие предположения он может сделать, когда бросает игральный кубик? Например, такие:
Ø событие А – выпадет цифра 1, 2, 3, 4, 5 или 6 – достоверное;
Ø событие В – выпадет цифра 7, 8 или 9 – невозможное;
Ø событие С – выпадет цифра 1 – случайное.
4) События несовместны, если появление одного из них исключает появление другого.
Два события, которые в данных условиях могут происходить одновременно, называют совместными, а те, которые не могут происходить одновременно, – несовместимыми.
5) События называются равновозможными, когда в их испытании нет преимуществ.
Среди данных событий указать пары, которые являются совместными, а какие – несовместимыми.
1. Таня и Ваня сыграли партию в шахматы:
а) Таня выиграла; Ваня проиграл; б) Таня проиграла; Ваня проиграл.
2. Брошен игральный кубик. На верхней грани оказалось:
а) число 6; число 5; б) число 6; четное число.
Суммой (объединением 
Произведением (пересечением 
Например. Пусть в опыте с бросанием игральной кости события: А – выпало число очков, кратное 2; В – выпало число очков, кратное 3. Тогда событие А + В означает, что выпало хотя бы одно из чисел 2, 3, 4, 6; событие АВ – выпало число 6.
Задача . Пусть из колоды вынимают одну карту. Рассмотрим события:
А – это король, В – это карта масти пик.
Тогда: А + В – вынут король или карта масти пик;
АВ – из колоды вынут король пик.
Для каждого события А можно рассмотреть противоположное событие Ā, которое наступит тогда и только тогда, когда событие А не наступает.
Например: А – выпадение чётного числа очков, Ā – выпадение нечетного числа очков; А – попадание в цель, Ā – промах.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №33. Вероятность события. Сложение вероятностей.
Перечень вопросов, рассматриваемых в теме:
— события, испытания, вероятность, случайное событие, невозможного и достоверного события;
— понятие классической вероятности события;
— поиск вероятности случайного события, пользуясь определением классической вероятности;
— поиск вероятности суммы событий.
Испытанием называется осуществление определенных действий.
Событие— факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Пространство элементарных событий Ω — множество всех различных исходов произвольного испытания.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Её ещё называют статистической вероятностью события.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 180-188.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
В корзине лежат клубки ниток зеленого и белого цвета. Бабушка просит внучку достать ей клубок ниток и, внучка наугад из корзины вынимает один клубок. Какое из следующих событий может произойти?
1) вынутый предмет окажется клубком
2) вынутый предмет окажется красным клубком
3) вынутый предмет окажется зеленым клубком
4) вынутый предмет не окажется клубком
Ответ: первое и третье.
1. Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.
Испытанием называется осуществление определенных действий.
Под событием понимают любой факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
События обычно обозначаются заглавными буквами латинского алфавита (А, В, С, D,…).
Рассматривая приведенный пример, мы можем сформулировать следующие заключения.
2. Определим еще несколько важных понятий теории вероятностей
Пространство элементарных событий Ω— множество всех различных исходов произвольного испытания.
Например, при броске одной игральной кости пространство элементарных событий Ω=
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Например, при бросании монеты не могут одновременно выпасть «Орёл» и «Решка».
Простейшим примером несовместных событий является пара противоположных событий.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Монету подбросили дважды. Укажите все элементарные события полной группы событий.
Элементарными событиями являются:
— Выпал один «орел» и одна «рещка».
3. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно подсчитать, как часто оно происходит.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Ее еще называют статистической вероятностью события.
Статистическая вероятность события рассчитывается опытным путем.
Еще со времен Древнего Китая за 2238 лет до нашей эры на основании метрик демографы обнаружили, что на каждую тысячу новорожденных приходится 514 мальчиков.
Это означает, что Вероятность рождения мальчика составляет 0,514.
1. Классическое определение вероятности применяется для равновозможных событий.
К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Например, при бросании игрального кубика события выпадения любого из очков равно возможны.
Рассмотрим произвольный эксперимент.
Пусть n— число всех исходов эксперимента, которые образуют полную группу попарно несовместных и равновозможных событий, m – число благоприятных событию А исходов. Тогда вероятностью события А называется число
Согласно определению вероятности наименьшее значение вероятности принимает невозможное событие, так как оно не может наступить и для него m=0, значит и вероятность равна 0.
Наибольшее значение принимает достоверное событие. В силу того, что оно гарантированно произойдет, для него m=n, Р=m/n=n/n=1.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Примеры и разбор решения заданий тренировочного модуля
Известна история о том, как однажды к Г. Галилею явился солдат и попросил помочь ему в решении насущного вопроса: какая сумма 9 или 10 очков при бросании трех костей выпадает чаще?
Может показаться, что шансы равны, так как каждая сумма из 9 и 10 очков может быть получена одним их шести способов:
9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3;
10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4.
Однако с учетом перестановок для суммы 9 очков получается 25 различными способами (по 6 способов для первого, второго, пятого вариантов суммы, по 3 способа для третьего и четвертого вариантов, 1 способ для последнего варианта 6 + 6 + 3 + 3 + 6 + 1), а для суммы 10 очков – 27 различными способами (6 + 6 + 3 + 6 + 3 + 3). Как видно, шансы этих случайных событий довольно близки между собой и относятся друг к другу как 25:27, что и вызвало затруднения солдата.
Таким образом, чаще выпадает сумма 10.
Пример 2. В средние века среди феодальной знати были широко распространены азартные игры. Большим любителем таких игра был француз шевалье де Мере. Страстного игрока в кости, придворного французского короля шевалье де Мере можно отнести к числу «основателей» теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял математиков решать различные задачи, на которые наталкивался сам во время своей практики игры. Он хотел разбогатеть при помощи игры в кости. Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
Одна из задач была поставлена следующим образом: Игральная кость бросается четыре раза. Шевалье бился об заклад, что при этом хотя бы один раз выпадет шесть очков. Какова вероятность выигрыша для шевалье? Ответ округлите до десятых.
Так как при каждом бросании игральной кости имеется 6 различных возможностей, то при четырех бросаниях кости число различных возможных случаев будет 6 · 6 · 6 · 6 = 1296.
Среди этих 1296 случаев будет 5 · 5 · 5 · 5 = 625 таких, где шестерка не выпадет ни разу.
В 1296 – 625 = 671 случае хотя бы один раз из четырех выпадает шестерка. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях кости равна 671/1296, что чуть больше 0,5.
События
Урок 25. Алгебра 11 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «События»
Сегодня на уроке мы напомним, чем занимается раздел математики, называемый теорией вероятностей. Назовём важнейшие понятия теории вероятностей. Узнаем, какие события называют случайными, достоверными и невозможными. Выясним, какие события называют элементарными. Поговорим о равновозможных событиях.
Из предыдущих классов вы уже имеете представление о теории вероятностей, теперь мы немного расширим и углубим их.
Итак, в первую очередь отметим, что важнейшими понятиями теории вероятностей являются вероятностный эксперимент (испытание, наблюдение), событие (следствие испытания) и вероятность события.
Вообще, событиями или явлениями называют всё, что происходит или не происходит в реальной действительности. Практикой установлено, что в часто происходящих случайных событиях существуют определённые закономерности. Раздел математики, который занимается исследованием этих закономерностей, называется теорией вероятностей.
Задача теории вероятностей – установление и математическое исследование закономерностей массовых случайных явлений.
Далее поговорим о событиях. Сформулируем определение. Событие называют случайным по отношению к некоторому испытанию (опыту), если в ходе этого испытания оно может произойти, а может и не произойти.
Например, при одном бросании игрального кубика испытание состоит в наблюдении выпавших очков. При проведении испытания возможны следующие события (исходы испытания): на верхней грани кубика может оказаться одно из чисел: 1, 2, 3, 4, 5, 6. Каждое из этих событий является случайным, так как оно может произойти, а может и не произойти.
Следующий пример. Пусть в урне находятся шары белого, красного и чёрного цвета, а испытание заключается в извлечении шара из урны. В результате однократного извлечения шара возможный три события (исхода испытания): «извлечён белый шар», «извлечён красный шар», «извлечён чёрный шар». Каждое из этих трёх событий является случайным, так как оно может произойти, а может и не произойти.
И ещё один пример. При однократном подбрасывании монеты возможны два исхода: выпадение орла и выпадение решки. Каждое из этих событий является случайным, так как оно может произойти, а может и не произойти.
Случайные события обычно обозначаются большими латинскими буквами 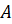
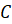
Событие 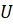
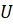
Так, например, при одном бросании игрального кубика появление одного из шести чисел 1, 2, 3, 4, 5, 6 будет достоверным событием, так как при бросании кубика оно обязательно произойдёт.
Если испытание заключается в извлечении одного шара из коробки, в которой лежат только красные шары, то извлечение красного шара будет достоверным событием.
Событие 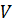
Пусть, например, в коробке находятся только красные шары, а испытание заключается в извлечении шара из коробки. Тогда событие «извлечён черный шар» является невозможным.
При бросании обычного игрального кубика выпадение числа 7 является невозможным событием.
Предположим, что в результате некоторого испытания обязательно происходит одно из событий и никакие два события не могут произойти одновременно, причём каждое из них не разделяется на более простые. Такие события называют элементарными событиями (или элементарными исходными испытаниями).
Приведём примеры элементарных событий. В испытании с бросанием игрального кубика существует 6 элементарных исходов: выпадение числа 1, выпадение числа 2, выпадение числа 3, выпадение числа 4, выпадение числа 5, выпадение числа 6.
При бросании монеты существует 2 элементарных события: выпадение орла и выпадение решки.
При извлечении одного шара из коробки, в которой находятся один белый шар, один красный шар и один чёрный шар, существует 3 элементарных исхода: извлечение белого шара, извлечение красного шара и извлечение чёрного шара.
Отметим, что рассмотренные в каждом из примеров события несовместны, то есть появление одного из событий исключает появление другого, и единственно возможны, то есть обязательно произойдёт одно из событий. Также в каждом из рассмотренных трёх примеров элементарные события являются равновозможными, то есть у каждого из событий шансы появиться одинаковы.
Кроме элементарных событий, в теории вероятностей рассматриваются и более сложные события. Например, при бросании игрального кубика может быть рассмотрено событие А – появление нечётного числа. Это событие «распадается» на три элементарных события: появление числа 1, появление числа 3 и появление числа 5.
А теперь давайте выполним несколько заданий.
Задание первое. Каким событием (достоверным, невозможным или случайным) является каждое из событий:
1) при комнатной температуре и нормальном атмосферном давлении сталь находится в жидком состоянии;
2) наугад вынутая из кошелька монета оказалась пятирублёвой;
3) наугад названное натуральное число больше нуля;
4) вынутый наугад цветок из букета ромашек оказался розой;
5) в результате броска игрального кубика появилось число 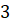
Задание второе. Перечислите все элементарные события, которые могут произойти в результате следующих испытаний:
1) на поверхность стола бросается игральный тетраэдр, грани которого пронумерованы числами 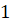
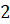
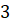
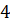
2) из коробки, в которой лежат семь шаров семи различных цветов, извлекается один шар и называется его цвет.
Задание третье. Выяснить, являются ли события 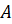
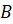
1) 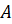
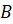
2) 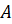
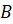
3) 
4)