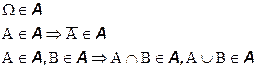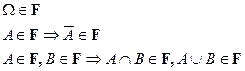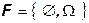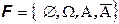что такое сигма алгебра событий
Глава 6 Решение задач по теме Сигма-алгебра
Конспект: Алиса Жильцова
дата: 30 сентября 2016 г.
6.1 Задача №1 (№ 2.35 в задачнике)
6.1.1 Условие задачи:
Приведите по два нетривиальных (т.е. \(\Omega\) и \(\emptyset\) не называть) примера такого события A, что:
Упростите выражения: \(\mathcal
6.1.2 Решение:
Приведём по два нетривиальных (т.е. \(\Omega\) и \(\emptyset\) не называть) примера такого события A, что:
Начнём с того, что \(\mathcal
\(\bullet\) A лежит в каждой \(\mathcal
Попробуем привести другой пример события, лежащего во всех \(\mathcal
Событие \(X_ <37>> 0\) означает, что в 37-м подбрасывании выпал орёл. Оно входит во все \(\mathcal
А этот пример еще интереснее! В нем есть ловушка! 🙂
Упростим следующие выражения:
Аналогично предыдущим пунктам получим: \(\mathcal
6.2 Задача №2 Про Агента 007 (№ 2.43 в задачнике)
6.2.1 Условие задачи
Сейчас либо солнечно, либо дождь, либо пасмурно без дождя. Соответственно множество \(\Omega\) состоит из трёх исходов, \(\Omega\) = <солнечно, дождь, пасмурно>. Джеймс Бонд пойман и привязан к стулу с завязанными глазами, но он может на слух отличать, идет ли дождь.
6.2.2 Решение задачи
Введём случайную величину Z, означающую то, что различает Джеймс Бонд. Другими словами, зная Z Джеймс Бонд с легкостью сможет сказать, идёт сейчас дождь или нет. Но он не отличает события <солнечно>и <пасмурно>.
Оформим возможные значения Z в виде таблицы:
| \(\Omega\) | Солнечно | Дождь | Пасмурно |
|---|---|---|---|
| Z | 0 | 1 | 0 |
На бытовом языке такую сигма-алгебру можем описать как список событий, который различает Джеймс Бонд, если бы ему завязали глаза и заткнули бы уши (печально!), т.е. если бы он не знал ничего.
Изобразим такие сигма-алгебры графически:
Ответ: таких сигма-алгебр существует всего 5!
6.3 Задача №3 (2.39 в задачнике)
6.3.1 Условие задачи (перевод)
6.3.2 Решение задачи
Прежде чем приступить к решению следует сразу разобраться в условии задачи. Выделим некоторые ключевые моменты, необходимые для понимания:
\(\bullet\) Первый момент не может являться локальным максимумом. В нашей последовательности \(X_0\) отсутствует, а значит, первый момент не берется в рассмотрение!
\(\bullet\) Для того, чтобы лучше понять, что же такое T, приведем пример с помощью картинки для последовательности (+1,+1,-1,-1,+1,-1):
На графике видим, что вторым локальным максимумом является точка (5,1), а момент T равен 6.
Интуитивно это можно представить так: Джон играет с ребятами, а в момент времени Т его зовёт бабушка Йоко. Что знает Джон? Он знает всё, что было до момента времени Т включительно, а что было после, он уже не видел. Что он может знать? Он знает, чему равно T.
Теперь, детально разобрав условие задачи, ответим на следующие вопросы.
\(\mathcal
Алгебра и сигма-алгебра



При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:
Алгебра событийAэто набор подмножеств пространства элементарных исходов 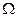
и для любой счетной последовательности
Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.
Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.
Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.
Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств
Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.
Зачем нам нужны сигма-алгебры для определения вероятностных пространств?
Может ли кто-нибудь объяснить простым языком, почему здание вероятности рухнет, если у нас не будет σ ‘ role=»presentation»> σ алгебры? Они просто вклиниваются посередине с этим невероятно каллиграфическим «F». Я верю, что они необходимы; Я вижу, что событие отличается от результата, но что было бы неправильно без σ ‘ role=»presentation»> σ алгебры?
Вопрос в том, в каком типе вероятностных задач определение вероятностного пространства, включающего σ ‘ role=»presentation»> σ алгебру, становится необходимостью?
Этот онлайн-документ на веб-сайте Дартмутского университета дает понятное объяснение на английском языке. Идея заключается в вращающемся указателе, вращающемся против часовой стрелки на окружности единицы периметра:
К первому пункту Сианя: когда вы говорите об алгебрах, вы спрашиваете об измеримых множествах, поэтому, к сожалению, любой ответ должен быть сосредоточен на теории меры. Я постараюсь довести это до конца нежно. σ ‘ role=»presentation»> σ
Теория вероятностей, допускающая все подмножества несчетных множеств, сломает математику
Но что, если область набора интересов не является четко определенной?
Хорошая новость: алгебры строго необходимы только для несчетных множеств σ ‘ role=»presentation»> σ
Поэтому на практике достаточно просто сделать это наблюдение достаточным для того, чтобы сделать наблюдение, в котором вы рассматриваете только измеримые по Лебегу множества, чтобы добиться прогресса в решении проблемы интересов.
Но подождите, что такое неизмеримый набор?
Боюсь, я могу только пролить немного света на это сам. Но парадокс Банаха-Тарского (иногда парадокс «солнца и гороха») может нам помочь:
Для заданного сплошного шара в трехмерном пространстве существует разложение шара на конечное число непересекающихся подмножеств, которые затем можно соединить по-разному, чтобы получить две идентичные копии исходного шара. Действительно, процесс сборки включает в себя только перемещение деталей и их вращение без изменения их формы. Однако сами кусочки являются не «твердыми телами» в обычном смысле, а бесконечным рассеянием точек. Реконструкция может работать всего с пятью частями.
Более сильная форма теоремы подразумевает, что при наличии любых двух «разумных» твердых объектов (таких как маленький шар и огромный шар) любой из них может быть повторно собран в другой. Об этом часто говорят неформально: «горох можно нарезать и снова собрать в Солнце» и называют «парадоксом гороха и солнца». 1
Чтобы разрешить этот парадокс, можно сделать одну из четырех уступок:
Теория вероятностей (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
В опыте обязательно произойдет одно и только одно из этих событий.
Любые два противоположных подмножества образуют полную группу подмножеств.
Если пространство элементарных исходов конечно или счетно, то сами элементарные исходы являются полной группой подмножеств.
Алгебра и сигма-алгебра
При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:
Алгебра событий A это набор подмножеств пространства элементарных исходов 
и для любой счетной последовательности
Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.
Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.
Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.
Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств
Если алгебра или сигма-алгебра содержит событие A, то она обязана содержать и отрицание A. Поэтому минимальное число подмножеств в нетривиальной сигма-алгебре равно 4.
Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.
Случайные события
Элемент сигма-алгебры в дальнейшем будем называть случайным событием.
Полная группа событий
Полная группа событий это полная группа подмножеств, каждое из которых является событием. Говорят, что события полной группы это разбиение пространства элементарных исходов.
Конечно-аддитивная функция
Пусть A – алгебра. Функция n, отображающая алгебру в множество действительных чисел
называется конечно-аддитивной, если для любого конечного набора попарно несовместных событий
Счетно-аддитивная функция
Пусть F – алгебра или сигма-алгебра. Функция
называется счетно-аддитивной, если она конечно-аддитивна и для любого счетного набора попарно несовместных событий
Конечная мера
Мера 
Вероятность
Вероятность (вероятностная мера) P это мера такая, что
С этого момента мы перестанем измерять вероятность в процентах и начнем измерять ее действительными числами от 0 до 1.
Когда вы пишите P всегда представляйте себе, какое пространство элементарных исходов и сигма-алгебра имеются в виду. Тогда вы сможете избежать многих ошибок
Обозначение P (Probability) для вероятности является стандартным, не стоит только забывать, что сама по себе (без определения пространства элементарных исходов и сигма-алгебры) вероятность не определена.
называют вероятностью события A
Вероятностное пространство
Вероятностное пространство это совокупность трех объектов – пространства элементарных исходов, сигма-алгебры событий и вероятности.
Это и есть математическая модель случайного явления или объекта.
Парадокс определения вероятностного пространства
Вернемся к исходной постановке задачи теории вероятностей. Нашей целью было построение математической модели случайного явления, которая помогла бы количественно оценить вероятности случайных событий. В то же время для построения вероятностного пространства необходимо задать вероятность, т. е. вроде бы именно то, что мы ищем (?).
Разрешение этого парадокса в том, что для полного определения вероятности как функции на всех элементах F, обычно достаточно задать ее на лишь на некоторых событиях из F, вероятность которых нам легко определить, а затем, пользуясь ее счетной аддитивностью, вычислить на любом элементе F.
Независимые события
Важным понятием теории вероятностей является независимость.
События A и B называются независимыми, если
т. е. вероятность одновременного осуществления этих событий равна произведению их вероятностей.
Попарно
События в счетном или конечном наборе называются независимыми попарно, если любая пара из них является парой независимых событий
В совокупности
События в счетном или конечном наборе называются независимыми в совокупности, если вероятность одновременного осуществления любого конечного поднабора из них равна произведению вероятностей событий этого поднабора.
Ясно, что независимые в совокупности события независимы и попарно. Обратное неверно.
Условная вероятность
Условной вероятностью события A при условии, что произошло событие B называется величина
Условную вероятность пока определим лишь для событий B, вероятность которых не равна нулю.
Если события A и B независимы, то
Свойства и теоремы
Простейшие свойства вероятности
Следует из того, что А и не-А противоположны и свойства конечной аддитивности вероятности
Вероятность противоположного события
Следует из того, что невозможное и достоверное события противоположны
Вероятность невозможного события
Следует из того, что
Монотонность вероятности
Следует из того, что любое событие содержится в пространстве элементарных исходов
Ограниченность вероятности
Следует из представления
Вероятность объединения событий
Следует из предыдущего
Полуаддитивность вероятности
Следует из счетной аддитивности вероятности и определения полной группы событий
Вероятности полной группы событий
Сумма вероятностей полной группы событий равна 1.
Следует из счетной аддитивности вероятности, определения полной группы событий и определения условной вероятности
Формула полной вероятности
Если вероятности всех событий полной группы больше нуля, то также
Следует из предудущей формулы и определения условной вероятности
Формула Байеса
Дискретная вероятностная модель
Вероятностное пространство называется дискретным, если его пространство элементарных исходов конечно или счетно.
В данном пункте мы переходим к описанию типовых математических моделей случайных событий. Начнем с простейшего случая.
Конечное пространство элементарных исходов
Пространство элементарных исходов называется конечным, если оно содержит конечное число элементарных исходов.
Классическая вероятностная модель
Классическая вероятностная модель
1. Конечное пространство элементарных исходов
2. Наибольшую сигма-алгебру (содержащую все подмножества пространства элементарных исходов).
3. Равномерную вероятностную меру, приписывающую равные вероятности всем элементарным исходам.
Из описания модели следует, что
· Любое подмножество пространства элементарных исходов является событием
· Любой элементарный исход имеет вероятность
Для того чтобы вероятность была конечно аддитивна
Вероятность любого события можно определить как
Априори – a priori, до опыта, т. е. с самого начала анализа до получения опытных данных.
Применять эту модель следует в тех случаях, когда априори ясно, что все исходы опыта симметричны (равновероятны).
Рассмотрим подробнее построение модели. Исходные данные для построения требуют, чтобы каждый элементарный исход имел одинаковую вероятность. Естественно потребовать, чтобы любое подмножество элементарных исходов было событием. Так как элементарные исходы образуют полную группу событий, то сумма их вероятностей должна быть равна 1, и из-за того, что все вероятности одинаковы, а количество элементарных исходов равно
Тогда для произвольного события A, используя конечную аддитивность вероятности получаем
Нетрудно проверить, что так определенная функция P будет вероятностью, и что требованиям модели удовлетворяет только одна такая функция. Следовательно, математическая модель определена однозначно.
Связь классической вероятностной модели с комбинаторикой
Вычисления в классической модели сводятся к комбинаторной задаче определения количества элементов в множестве и его подмножествах. С другой стороны, если каким-либо иным образом узнать вероятность события в классической модели, то можно определить количество элементарных исходов в нем, т. е решить комбинаторную задачу методами теории вероятностей. Напомним некоторые формулы комбинаторики.
Основная формула комбинаторики
и количество разных значений первой координаты равно n, а второй m. Тогда количество разных элементарных исходов равно m*n. Для доказательства достаточно представить все варианты в виде прямоугольной таблицы, строки которой пронумерованы значениями первой, а столбцы – второй координаты. Применяя индукцию можно распространить эту формулу на вектора с n координатами.
И этой формулы следует в частности, что количество всех двоичных векторов размерности n равно 2 n. И что количество всех подмножеств конечного множества с n элементами равно 2 n. И что количество различных вариантов выпадения очков на трех игральных костях равно 216. И т. д……
Факториал
Количество всех различных перестановок n различных чисел равно
Формула Стирлинга
Для приближенного вычисления факториалов больших чисел используется формула Стирлинга
Биномиальный коэффициент
Количество двоичных векторов размерности n с ровно k единицами равно
Бином Нютона
Полиномиальная формула
Схема выбора с возвращением
Частным случаем классической вероятностной модели является так называемая схема выбора с возвращением. Элементарный исход – это вектор
Схема является примером того, как можно строить сложные вероятностные модели из более простых. Эта схема применяется для описания ситуаций, в которых некоторый простой опыт с N возможными равновероятными исходами повторяется n раз.
Название схема получила от следующей ее интерпретации.
В урне находится N различных шаров. Из урны случайно вынимается один шар и записывается его номер
После этого шар возращается обратно в урну, и опыт поворяется снова (всего n раз).
Пример вычисления вероятности события в схеме выбора с возвращением.
Игральная кость бросается 20 раз. Найти вероятность того, что выпадет 2 единицы, 4 пятерки, 3 шестерки (событие A)
В этом случае n=20, N=6.
Обратите внимание, что мы не ищем сразу вероятность исходного события, а придумываем как легче выразить это событие через другие, вероятность которых легче подсчитать
Следовательно, вероятность равна
Осталось сложить вероятности всех подходящих событий и найти вероятность A
Суммирование ведется по всем возможным значениям индексов, удовлетворяющих условиям. В частности, по i1=1, по i2 от 1 до 6, по i3 от 1 до 6 и т. д.
Попробуйте вычислить эту вероятность.
Вычисление этой вероятности не так то просто даже при наличии компьютера. Для этого придется написать небольшую программу.