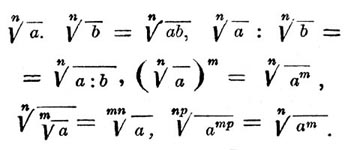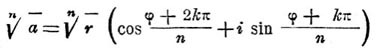что такое радикал в алгебре

Радикал, в математике

Полезное

Смотреть что такое «Радикал, в математике» в других словарях:

РАДИКАЛ (в математике) — РАДИКАЛ, математический знак (измененное латинское r), которым обозначают действие извлечения корня, а также результат извлечения корня, т. е. число вида … Энциклопедический словарь

Радикал в математике — Один из корней двучленного уравнения xn = а называется радикалом и обозначается Здесь а называется подкоренным числом, n показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

РАДИКАЛ — (лат., radix, radicis корень). 1) Политик, стремящийся к коренным преобразованиям в управлении страны. 2) английские социалисты носят также название радикалов. 3) В органической химии сложные вещества, способные соединяться с другими веществами… … Словарь иностранных слов русского языка

радикал — РАДИКАЛ, а, муж. 1. Сторонник радикализма (в 1 знач.), член радикальной партии. 2. Приверженец крайних, решительных действий, взглядов. | прил. радикалистский, ая, ое. II. РАДИКАЛ, а, муж. 1. В математике: знак, (Ц) обозначающий извлечение корня… … Толковый словарь Ожегова

РАДИКАЛ — (от лат. radicalis коренной) многозначный термин, используемый в разных науках (напр., в химии и математике) и практиках. 1, Сторонник радикальных (крайних, решительных) взглядов и действий, партий, движений. Бескомпромиссный человек. Склонность… … Большая психологическая энциклопедия

Радикал — В Викисловаре есть статья «радикал» Радикал (буквально: «коренной» от лат. radix … Википедия

РАДИКАЛ — Основное значение имеющий отношение к корню. Таким образом: 1. В математике знак (V), выражающий операцию разложения числа, стоящего под ним, на его корни. 2. В социальных/политических терминах описание любой точки зрения или предложения, в… … Толковый словарь по психологии

Центр (в математике) — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Вербицкий, Михаил Сергеевич — В Википедии есть статьи о других людях с такой фамилией, см. Вербицкий. Михаил Вербицкий … Википедия

Абель Нильс Хенрик — (Abel) (1802 1829), норвежский математик. Доказал, что алгебраические уравнения степени выше 4 й в общем случае неразрешимы в радикалах. Изучал интегралы от алгебраических функций (абелевы интегралы). Один из создателей теории эллиптических… … Энциклопедический словарь

Источник

Радикал в математике

Здесь а называется подкоренным числом, n — показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р. подразумевается число положительное. Алгебраическое выражение, содержащее Р., может подвергаться преобразованиям при помощи формул:

a = r (cos φ + i sin φ), где r > 0.

Для n значений Р. получается выражение

где k = 0, 1, 2. n— 1. В правой части

Полезное

Смотреть что такое «Радикал в математике» в других словарях:

РАДИКАЛ (в математике) — РАДИКАЛ, математический знак (измененное латинское r), которым обозначают действие извлечения корня, а также результат извлечения корня, т. е. число вида … Энциклопедический словарь

Радикал, в математике — Один из корней двучленного уравнения xn = а называется радикалом и обозначается Здесь а называется подкоренным числом, n показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

РАДИКАЛ — (лат., radix, radicis корень). 1) Политик, стремящийся к коренным преобразованиям в управлении страны. 2) английские социалисты носят также название радикалов. 3) В органической химии сложные вещества, способные соединяться с другими веществами… … Словарь иностранных слов русского языка

радикал — РАДИКАЛ, а, муж. 1. Сторонник радикализма (в 1 знач.), член радикальной партии. 2. Приверженец крайних, решительных действий, взглядов. | прил. радикалистский, ая, ое. II. РАДИКАЛ, а, муж. 1. В математике: знак, (Ц) обозначающий извлечение корня… … Толковый словарь Ожегова

РАДИКАЛ — (от лат. radicalis коренной) многозначный термин, используемый в разных науках (напр., в химии и математике) и практиках. 1, Сторонник радикальных (крайних, решительных) взглядов и действий, партий, движений. Бескомпромиссный человек. Склонность… … Большая психологическая энциклопедия

Радикал — В Викисловаре есть статья «радикал» Радикал (буквально: «коренной» от лат. radix … Википедия

РАДИКАЛ — Основное значение имеющий отношение к корню. Таким образом: 1. В математике знак (V), выражающий операцию разложения числа, стоящего под ним, на его корни. 2. В социальных/политических терминах описание любой точки зрения или предложения, в… … Толковый словарь по психологии

Центр (в математике) — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Вербицкий, Михаил Сергеевич — В Википедии есть статьи о других людях с такой фамилией, см. Вербицкий. Михаил Вербицкий … Википедия

Абель Нильс Хенрик — (Abel) (1802 1829), норвежский математик. Доказал, что алгебраические уравнения степени выше 4 й в общем случае неразрешимы в радикалах. Изучал интегралы от алгебраических функций (абелевы интегралы). Один из создателей теории эллиптических… … Энциклопедический словарь

Источник

Математическая энциклопедия
РАДИКАЛЫ

Общая теория радикалов. Всюду в дальнейшем говорится только об алгебрах (имеются в виду алгебры над произвольным фиксированным ассоциативно-коммутативным кольцом с единицей); кольца являются частным случаем таких алгебр. Под идеалом алгебры, если это не оговорено специально, понимается двусторонний идеал.

(A) гомоморфный образ r-алгебры есть r-алгебра;

(Б) каждая алгебра Акласса обладает наибольшим r-идеалом, т. е. идеалом, содержащим любой r-идеал этой алгебры, и этот максимальный r-идеал наз. тогда r-радикалом этой алгебры и обозначается r(А).

Алгебра, совпадающая со своим Р., наз. радикальной. В любом классе алгебр и для любого радикала <0>является единственной одновременно радикальной и полупростой алгеброй. Подпрямое произведение любого множества полупростых алгебр само полупросто.

С каждым радикалом r связаны два подкласса алгебр в : класс (r) всех r-радикальных алгебр и класс (r) всех r-полупростых алгебр. По любому из этих классов однозначно находится радикал r(А).для каждой алгебры Аиз , а именно:

Алгебра r-радикальна тогда и только тогда, когда она не может быть отображена гомоморфно ни на одну ненулевую r-полупростую алгебру.

Известны условия на подклассы алгебр, необходимые и достаточные для того, чтобы эти подклассы служили классами всех радикальных или классами всех полупростых алгебр для каких-либо Р. в . Такие подклассы алгебр принято называть соответственно радикальными и полупростыми подклассами.

Наследственные радикалы. Радикал r наз. идеальо наследственным радикалом, или кручением, в классе , если для всякого идеала I алгебры Аэтого класса: Идеально наследственные Р. есть в точности те Р., для к-рых классы (r). и (r) замкнуты относительно идеалов. Радикал rназ. наследственным, если класс (r) замкнут относительно идеалов. В классах ассоциативных, а также альтернативных алгебр каждый наследственный Р. является кручением. Радикал r наз. строго наследственным, если класс (r) замкнут относительно подалгебр.

Класс всех кручений является полной дистрибутивной «решеткой» (см. Дистрибутивная решетка). Употребление кавычек здесь связано с тем, что совокупность элементов этой «решетки» является не множеством, а классом.

Лит.:[1] A m i t s u r S. A., «Amer. J. Math.», 1952, v. 74, p. 774-86: 1954, v. 76, p. 100-36; [2] К у р о ш А. Г.,»Матем. сб.», 1953, т. 33, в. 1, с. 13-26; [3] D i v i n s k у N.. Rings and radicals, Toronto, 1965;[4] A r t i n E., N e s b i t t С., Т h o r a l l R., Rings with minimum condition, Ann Arbor, 1944; [5] Итоги науки. Алгебра. Топология. Геометрия. 1967, М., 1969, с. 28-32; [6] Кольца, т. 2, Новосиб., 1973, с. 3-6; [7] А н д р у н а к и е в и ч В. А., Р я б у х и н Ю. М., Радикалы алгебр и структурная теория, М., 1979; [8] Ж е в л а к о в К. А., С л и н ь к о А. М., Ш е с т а к о в И. П., Ширшов А. И., Кольца, близкие к ассоциативным, М., 1978.

Лит.:[1] Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964; [2] Теория алгебр Ли. Топология групп Ли. Семинар «Софус Ли», пер. с франц., М., 1962; [3] Ш е в а л л е К., Теория групп Ли, пер. с франц., т. 3, М., 1958. А. Л. Онищик.

Источник

РАДИКАЛ (в математике)

Смотреть что такое «РАДИКАЛ (в математике)» в других словарях:

Радикал в математике — Один из корней двучленного уравнения xn = а называется радикалом и обозначается Здесь а называется подкоренным числом, n показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Радикал, в математике — Один из корней двучленного уравнения xn = а называется радикалом и обозначается Здесь а называется подкоренным числом, n показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

РАДИКАЛ — (лат., radix, radicis корень). 1) Политик, стремящийся к коренным преобразованиям в управлении страны. 2) английские социалисты носят также название радикалов. 3) В органической химии сложные вещества, способные соединяться с другими веществами… … Словарь иностранных слов русского языка

радикал — РАДИКАЛ, а, муж. 1. Сторонник радикализма (в 1 знач.), член радикальной партии. 2. Приверженец крайних, решительных действий, взглядов. | прил. радикалистский, ая, ое. II. РАДИКАЛ, а, муж. 1. В математике: знак, (Ц) обозначающий извлечение корня… … Толковый словарь Ожегова

РАДИКАЛ — (от лат. radicalis коренной) многозначный термин, используемый в разных науках (напр., в химии и математике) и практиках. 1, Сторонник радикальных (крайних, решительных) взглядов и действий, партий, движений. Бескомпромиссный человек. Склонность… … Большая психологическая энциклопедия

Радикал — В Викисловаре есть статья «радикал» Радикал (буквально: «коренной» от лат. radix … Википедия

РАДИКАЛ — Основное значение имеющий отношение к корню. Таким образом: 1. В математике знак (V), выражающий операцию разложения числа, стоящего под ним, на его корни. 2. В социальных/политических терминах описание любой точки зрения или предложения, в… … Толковый словарь по психологии

Центр (в математике) — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Вербицкий, Михаил Сергеевич — В Википедии есть статьи о других людях с такой фамилией, см. Вербицкий. Михаил Вербицкий … Википедия

Абель Нильс Хенрик — (Abel) (1802 1829), норвежский математик. Доказал, что алгебраические уравнения степени выше 4 й в общем случае неразрешимы в радикалах. Изучал интегралы от алгебраических функций (абелевы интегралы). Один из создателей теории эллиптических… … Энциклопедический словарь

Источник

РАДИКАЛЫ

Общая теория радикалов. Всюду в дальнейшем говорится только об алгебрах (имеются в виду алгебры над произвольным фиксированным ассоциативно-коммутативным кольцом с единицей); кольца являются частным случаем таких алгебр. Под идеалом алгебры, если это не оговорено специально, понимается двусторонний идеал.

(A) гомоморфный образ r-алгебры есть r-алгебра;

(Б) каждая алгебра Акласса обладает наибольшим r-идеалом, т. е. идеалом, содержащим любой r-идеал этой алгебры, и этот максимальный r-идеал наз. тогда r-радикалом этой алгебры и обозначается r(А).

Алгебра, совпадающая со своим Р., наз. радикальной. В любом классе алгебр и для любого радикала <0>является единственной одновременно радикальной и полупростой алгеброй. Подпрямое произведение любого множества полупростых алгебр само полупросто.

С каждым радикалом r связаны два подкласса алгебр в : класс (r) всех r-радикальных алгебр и класс (r) всех r-полупростых алгебр. По любому из этих классов однозначно находится радикал r(А).для каждой алгебры Аиз , а именно:

Алгебра r-радикальна тогда и только тогда, когда она не может быть отображена гомоморфно ни на одну ненулевую r-полупростую алгебру.

Известны условия на подклассы алгебр, необходимые и достаточные для того, чтобы эти подклассы служили классами всех радикальных или классами всех полупростых алгебр для каких-либо Р. в . Такие подклассы алгебр принято называть соответственно радикальными и полупростыми подклассами.

Частичная упорядоченность радикальных классов по включению индуцирует частичный порядок на классе всех Р. в 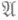. А именно, считается, что , если (r 1 ) содержит (r 2 ) (и в этом случае также (r 1 ) содержит (r 2 )).

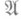
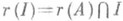
Наследственные радикалы. Радикал r наз. идеальо наследственным радикалом, или кручением, в классе , если для всякого идеала I алгебры Аэтого класса: Идеально наследственные Р. есть в точности те Р., для к-рых классы (r). и (r) замкнуты относительно идеалов. Радикал rназ. наследственным, если класс (r) замкнут относительно идеалов. В классах ассоциативных, а также альтернативных алгебр каждый наследственный Р. является кручением. Радикал r наз. строго наследственным, если класс (r) замкнут относительно подалгебр.

Класс всех кручений является полной дистрибутивной «решеткой» (см. Дистрибутивная решетка). Употребление кавычек здесь связано с тем, что совокупность элементов этой «решетки» является не множеством, а классом.

— верхний Р., определяемый классом всех матричных колец над телами;

В классе колец с условием минимальности первые семь Р. совпадают и соответствуют классическому Р. Если радикал r индуцирует в классе колец с условием минимальности классический Р., то . Для колец с условием максимальности . Для коммутативных колец , . Радикалы , являются специальными. Радикалы j, b, соответствуют одному и тому же разбиению простых колец, а -другим попарно различным разбиениям.

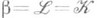
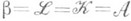
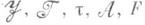
Лит.:[1] A m i t s u r S. A., «Amer. J. Math.», 1952, v. 74, p. 774-86: 1954, v. 76, p. 100-36; [2] К у р о ш А. Г.,»Матем. сб.», 1953, т. 33, в. 1, с. 13-26; [3] D i v i n s k у N.. Rings and radicals, Toronto, 1965;[4] A r t i n E., N e s b i t t С., Т h o r a l l R., Rings with minimum condition, Ann Arbor, 1944; [5] Итоги науки. Алгебра. Топология. Геометрия. 1967, М., 1969, с. 28-32; [6] Кольца, т. 2, Новосиб., 1973, с. 3-6; [7] А н д р у н а к и е в и ч В. А., Р я б у х и н Ю. М., Радикалы алгебр и структурная теория, М., 1979; [8] Ж е в л а к о в К. А., С л и н ь к о А. М., Ш е с т а к о в И. П., Ширшов А. И., Кольца, близкие к ассоциативным, М., 1978.

В классе алгебр Ли обычно радикалом наз. наибольший разрешимый идеал, т. е. разрешимый идеал r содержащий все разрешимые идеалы данной алгебры Ли. В конечномерной алгебре Ли существует также наибольший нильпотентный идеал n (называемый иногда нильрадикалом), к-рый совпадает с наибольшим идеалом, состоящим из нильпотентных элементов, а также с множеством таких , что присоединенный оператор adx содержится в Р. ассоциативной алгебры линейных преобразований пространства , порожденной присоединенной алгеброй Ли . Рассматривается также нильпотентный радикал алгебры Ли — это множество таких что s(x) = 0 для любого неприводимого конечномерного линейного представления s алгебры . Нильпотентный Р. совпадает также с наибольшим из идеалов, представляемых нильпотентными операторами при любом конечномерном линейном представлении алгебры При этом . Если характеристика основного поля равна 0, то — это наименьший из идеалов , для к-рых — редуктивная алгебра Ли. В этом случае нильпотентный Р. связан с радикалом r, соотношениями

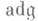
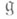
любое дифференцирование алгебры Ли переводит и . Нильрадикал и нильпотентный Р., однако, не являются Р. в смысле общей теории Р. колец и алгебр.

Лит.:[1] Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964; [2] Теория алгебр Ли. Топология групп Ли. Семинар «Софус Ли», пер. с франц., М., 1962; [3] Ш е в а л л е К., Теория групп Ли, пер. с франц., т. 3, М., 1958. А. Л. Онищик.

Источник