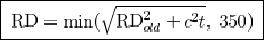Что такое отклонение по глико в шахматах
Коротко о сложном. Рейтинговая система Глико-Ленга. [Часть 1]
Всем привет. Совсем недавно Valve рассказала по какой методике идет подсчёт ранга в Underlords. Многие из Вас не знают, что такое система Глико и моя цель донести до больших масс, как это работает. Для начала я познакомлю вас с первой рейтинговой системой, которая многим известна по шахматам.

Система ЭЛО делит игроков на множество разрядов, которые имеют дельту в 200 очков. Многие наши читатели занимались шахматами, поэтому знают, что это из себя представляет. Разница хотя бы в 200 очков уже является пропастью в один разряд.
Система ЭЛО и была попыткой справедливо оценивать результаты игр. Победа слабого над сильным являлась большим ударом по рейтинговой ситуации фаворита.
Давайте перейдем к формулам.
По данной формуле вычисляется математическое ожидание победы игрока A над B. В этом нет ничего сложного. Например:
Команда NaVi имеет 2200 очков ЭЛО, а VirtusPro имеет целых 2500. Как мы можем определить с какой вероятностью более слабая команда победит фаворита? Подставим их рейтинги.
В результате мы видим, что шанс победы NaVi всего 15%, соответственно их противники выиграют с вероятностью в 85%
И вот произошла сенсация, NaVi победили и оказались в финале, на сколько же увеличился их рейтинг? Чтобы посчитать это, мы будем использовать данную формулу:
Посчитаем рейтинг NaVi после победы над VP.
Целых 17 очков получили NaVI. Соответственно за ничью они бы получили в два раза меньше очков. Но что будет при поражение?
Они потеряли всего 3 очка, так как были изначально слабее соперников. Теперь давайте посмотрим изменения у VP после победы и поражения. Напомним, что коэффициент у них будет меньше.
Победа практически ничего им не дала. Всего 1.5 очка. Ничья вообще бы ничего им не дала. А вот поражение.
Таким образом VP потеряли бы 9 очков, напоминаю, что NaVi потеряли всего 3.
Данная система не является полностью справедливой и поэтому есть множество ее аналогов и доработок. Именно система Глико и является улучшением системы ЭЛО. Ее мы и разберем в следующей части.
Глико
Система Глико применяется в настоящий момент на свободном интернетовском шахматном сервере (FICS), а вариации системы Глико были приспособлены для нескольких коммерческих интернетовских игровых организаций, таких как ChronX, Case’s Ladder и других.
Вы можете соглашаться со мной или нет, но, по моему мнению, самым большим очарованием для игроков шахматных турниров или соперников в других видах спорта является измерение их игровой силы. Система ранжирования Эло, разработанная в начале 60-х Арпадом Эло, была первой шахматной системой ранжирования, которая несла в себе вероятностную основу. Позже она была принята многими шахматными федерациями и даже организациями, отвечающими за такие игры, как Scrabble, настольный теннис и т.д. Хоть система Эло и является значительным шагом вперед по отношению к более ранним системам, у нее тоже есть свои проблемы. В 1995 году, в ответ на имеющиеся там недостатки, я создал систему ранжирования Глико. Система моя получена путем рассмотрения статистической модели исходов шахматных игр, и принятия затем математических приближений, позволяющих простейшие вычисления. Система Эло является одним из специальных случаев моей системы.
Проблема системы Эло, которую исправляет система Глико, это достоверность рейтинга игрока. Предположим, что два игрока, оба с коэффициентом Эло в 1700, встречаются на турнире, и первый побеждает второго. По версии Американской Шахматной Федерации системы Эло первый игрок получит в этом случае 16 рейтинговых очков, а второй игрок потеряет те же 16 очков. Но предположим, что первый игрок только что вернулся к играм на турнирах после многих лет «отдыха», а второй игрок режется в шахматы каждый выходной. В этой ситуации рейтинг первого игрока в 1700 очков является не совсем достоверным отражением его силы, в то время как рейтинг второго игрока в 1700 является вполне реальным отображением его игрового мастерства. Моя интуиция подсказывает мне, что (1) рейтинг первого игрока должен увеличиться намного (больше 16-ти), поскольку его рейтинг не совсем реален, и то, что он побил игрока с практически точным рейтингом в 1700 очевидно наводит на мысль, что его сила заведомо превышает 1700, и (2) рейтинг второго игрока должен немного уменьшиться (менее 16-ти очков), поскольку про его рейтинг и так уже известно, что а) он находится в районе 1700, и б) он проиграл игроку, чей рейтинг не заслуживает доверия, и потому о его собственной игровой силе могут быть сделаны лишь небольшие догадки.
Хоть большинство ситуаций не столь экстремальны, мне кажется, что в систему ранжирования полезно включить меру достоверности чьего-либо рейтинга. Потому-то система Глико и превосходит систему Эло, что вычисляет не только рейтинг R, который может быть представлен, как «наилучшая догадка» о чьей-либо игровой силе, но и «рейтинговое отклонение» (RD) (в статистической терминологии, стандартное отклонение), которое измеряет неопределенность рейтинга. Высокие RD отвечают ненадежным рейтингам, указывая, что игрок выступает не часто или что игрок участвовал лишь в небольшом количестве игр. Низкий RD указывает на то, что игрок постоянно принимает участие в турнирах.
В системе Глико игровой рейтинг изменяется только по прошествии игр, но его RD изменяется и после окончания игры, и по прошествии времени, в течение которого игрок не принимал участия в турнирах. Одним из свойств Системы является то, что сыгранные матчи всегда уменьшают RD игрока, а время, проведенное вне турниров, всегда его увеличивает. Смысл этого заключается в том, что чем больше сыграно игр, тем больше информации о способностях игрока получено, и тем точнее становится рейтинг. Время идет, и мы начинаем сомневаться в силе игрока, и это находит свое отражение в возрастании RD.
Обратите внимание, что в системе Глико изменения в рейтинге не столь сбалансированы, как это есть в системе Эло. Если рейтинг одного игрока возрос на x очков, то совсем необязательно, что рейтинг его соперника уменьшится на те же x очков. Фактически в системе Глико количество очков, на которое уменьшится рейтинг соперника, регулируется значениями RD обоих игроков.
Поскольку игрок в системе Глико имеет и рейтинг, и RD, то обычно более информативно описать силу игрока в виде интервала (нежели просто указать его значение). Одним из путей является создание 95% доверительного интервала. Наименьшим значением интервала является рейтинг игрока минус двойной RD, а наивысшим значением является рейтинг игрока плюс двойной RD. Так, например, если чей-либо рейтинг равен 1850 и RD равно 50, то интервал будет простираться между 1750 и 1950. Мы можем сказать тогда, что мы на 95% уверены, что реальная сила игрока лежит находится между 1750 и 1950. Если у игрока низкий RD, то интервал будет уже, и мы будем на 95% уверены в реальной силе игрока в меньшем интервале значений.
Формулы:
Чтобы применить рейтинговый алгоритм, будем считать, что игры внутри «рейтингового периода» происходят одновременно. Период этот может быть и несколько месяцев, и одна минута. В первом случае берутся рейтинги и RD игроков на начало рейтингового периода, затем рассмотриваются исходы встреч, и в конце периода вычисляются обновленные рейтинги и RD (которые потом в свою очередь будут использованы как начальные рейтинги и RD для последующего рейтингового периода). Когда период равен минуте, рейтинги и RD будут обновляются на поматчевой основе (именно этой системой пользуется FICS). Система Глико работает наилучшим образом, когда число игр в рейтинговом периоде невелико, скажем в среднем 5-10 на одного игрока за период. Длина времени рейтингового периода есть воля администратора.
Шаг 1. Определим рейтинг и RD для каждого игрока в начале рейтингового периода.
(а) Игрок еще не включенный в рейтинги получает 1500 очков рейтинга и RD, равный 350.
(б) В противном случае, используя наипоследнейший рейтинг, и вычислив новый RD из старого RD (RDold) по формуле:
Шаг 2. Для обновления рейтинга каждого игрока по отдельности выполняются следующие вычисления:
Пусть r’ и RD’ означают рейтинги и рейтинговые отклонения на момент окончания рейтингового периода. Тогда формулы обновления рейтинга и рейтинговых отклонений примут следующий вид:
Эти вычисления следует выполнить для каждого игрока, попавшего в рейтинговый период.
Пример:
Для демонстрации Шага 2 предположим, что игрок с рейтингом в 1500 сыграл матчи против 1400, 1550 и 1700, выиграв первую встречу и проиграв две оставшиеся. Предположим, что отклонение рейтинга этого игрока равно 200, а у его оппонентов 30, 100, и 300 соответственно.
отклонение Глико
RD измеряет точность рейтинга игрока, при этом один RD равен одному стандартному отклонению. Например, игрок с рейтингом 1500 и RD 50 имеет реальную силу от 1400 до 1600 (два стандартных отклонения от 1500) с уверенностью 95%. Дважды RD добавляется и вычитается из их рейтинга, чтобы вычислить этот диапазон. После игры величина изменения рейтинга зависит от RD: изменение меньше, когда RD игрока низкое (поскольку их рейтинг уже считается точным), а также, когда RD противника высокое (поскольку истинный рейтинг противника не очень хорошо известно, поэтому мало информации получается). RD само по себе уменьшается после игры, но оно постепенно увеличивается с течением времени бездействия.
Спасибо за информацию!
почему бы тогда сразу не умножить на 2 и писать реальную цифру по Глико?)
Модификатор RD не может быть постоянным (поэтому «реальных цифр» и не будет), и его (модификатор) и нужно сразу умножать на 2, по-другому и не подсчитывают.
Система по Глико не предназначена для определения чего-то (и уж тем более про реальный рейтинг). Это модификатор для изменения в подсчетах, который (модификатор) зависит от того, как часто или редко вы играете! Чем реже вы играете, тем сильнее прирост изменения рейтинга, а чем чаще вы играете, тем слабее прирост к изменениям в рейтинге.
Ключевая фишка системы Глико в этом: «RD само по себе уменьшается после игры, но оно постепенно увеличивается с течением времени бездействия«.
М.Е. Гликман: система ГЛИКО
В статье «Система рейтингования Глико» профессор М.Е. Гликман из Бостонского университета представил свой вариант решения проблемы рейтинга. Проблема системы Эло, которую исправляет система Глико, это достоверность рейтинга игрока. Предположим, что два игрока, оба с коэффициентом Эло в 1700, встречаются на турнире, и первый побеждает второго. По версии Американской Шахматной Федерации системы Эло первый игрок получит в этом случае 16 рейтинговых очков, а второй игрок потеряет те же 16 очков. Но предположим, что первый игрок только что вернулся к играм на турнирах после многих лет «отдыха», а второй игрок режется в шахматы каждый выходной. В этой ситуации рейтинг первого игрока в 1700 очков является не совсем достоверным отражением его силы, в то время как рейтинг второго игрока в 1700 является вполне реальным отображением его игрового мастерства. Моя интуиция подсказывает мне, что (1) рейтинг первого игрока должен увеличиться намного (больше 16), поскольку его рейтинг не совсем реален, и то, что он побил игрока с практически точным рейтингом в 1700 очевидно наводит на мысль, что его сила заведомо превышает 1700, и (2) рейтинг второго игрока должен немного уменьшиться (менее 16-ти очков), поскольку про его рейтинг и так уже известно, что а) он находится в районе 1700, и б) он проиграл игроку, чей рейтинг не заслуживает доверия, и потому о его собственной игровой силе могут быть сделаны лишь небольшие догадки.
Смысл этого заключается в том, что чем больше сыграно игр, тем больше информации о способностях игрока получено и тем точнее становится рейтинг. Время идет, и мы начинаем сомневаться в силе игрока, и это находит свое отражение в возрастании RD. Если рейтинг одного игрока возрос на х очков, то совсем необязательно, что рейтинг его соперника уменьшится на те же х очков. Фактически в системе Глико количество очков, на которое уменьшится рейтинг соперника, регулируется значениями RD обоих игроков.
Шаг 1. Определим рейтинг и RD для каждого игрока в начале рейтингового периода.
где t — число рейтинговых периодов со дня последней игры (т. е. если ранжируемый играл в самом последнем из рейтинговых периодов, то t = 1), а с является константой, регулирующей увеличение неопределенности со временем.
Выбор с мы обсудим чуть ниже. Вышеописанная формула гарантирует, что RD в начале рейтингового периода никогда не будет больше 350 — значения RD для необсчитанного игрока.
Шаг 2. Для обновления рейтинга каждого игрока по отдельности выполняются следующие вычисления.
Пусть г’ и RD’ означают рейтинги и рейтинговые отклонения на момент окончания рейтингового периода. Тогда формулы обновления рейтинга и рейтинговых отклонений примут следующий вид:
400 yjl + 3q 2 (RDj) jn 2
Эти вычисления следует выполнить для каждого игрока, попавшего в рейтинговый период.
Пример. Для демонстрации Шага 2 предположим, что игрок с рейтингом в 1500 сыграл матчи против 1400, 1550 и 1700, выиграв первую встречу и проиграв две оставшиеся. Предположим, что отклонение рейтинга этого игрока равно 200, а у его оппонентов 30, 100 и 300 соответственно. Результаты сведены в табл. 6.10.
Рейтинговая система Glicko
RD измеряет точность рейтинга игрока, при этом один RD равен одному стандартному отклонению. Например, игрок с рейтингом 1500 и RD 50 имеет реальную силу от 1400 до 1600 (два стандартных отклонения от 1500) с достоверностью 95%. Дважды (точно: 1,96) RD добавляется и вычитается из их рейтинга, чтобы вычислить этот диапазон. После игры величина изменения рейтинга зависит от RD: изменение меньше, когда RD игрока низкое (так как его рейтинг уже считается точным), а также когда RD его оппонента высок (поскольку истинный рейтинг противника не равен хорошо известно, поэтому информации собирается мало). Само значение RD уменьшается после игры, но со временем бездействия оно будет медленно увеличиваться.
Шаг 1. Определите RD
Шаг 2: Определите новый рейтинг
Новые рейтинги после серии m игр определяются по следующему уравнению:
грамм ( р D я ) знак равно 1 1 + 3 q 2 ( р D я 2 ) π 2 <\ displaystyle g (RD_ ) = <\ frac <1> <\ sqrt <1 + <\ frac <3q ^ <2>(RD_ ^ <2>)> <\ pi ^ <2>>>>>>>
Шаг 3. Определение нового отклонения рейтингов
Функция предыдущего расчета RD заключалась в том, чтобы соответствующим образом увеличить RD, чтобы учесть возрастающую неопределенность в уровне навыков игрока в период отсутствия наблюдения со стороны модели. Теперь RD обновляется (уменьшается) после серии игр: