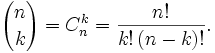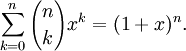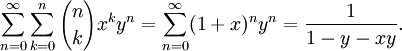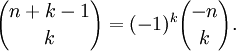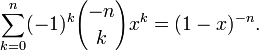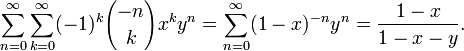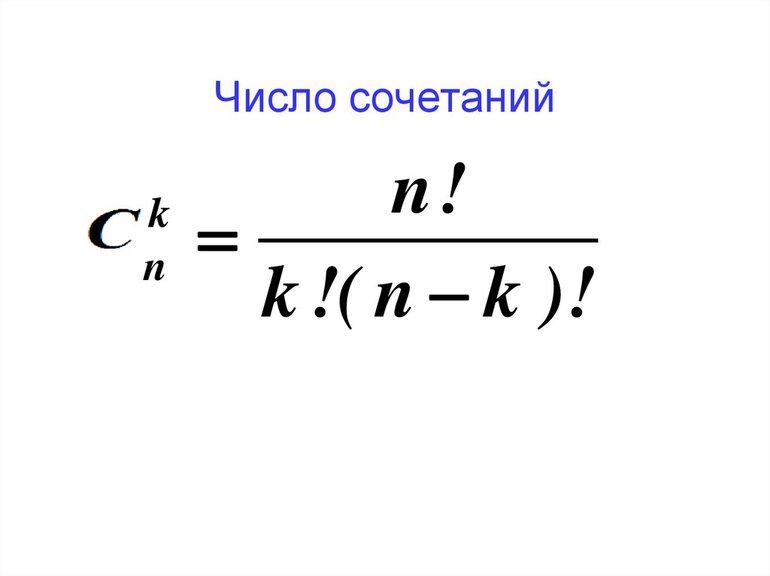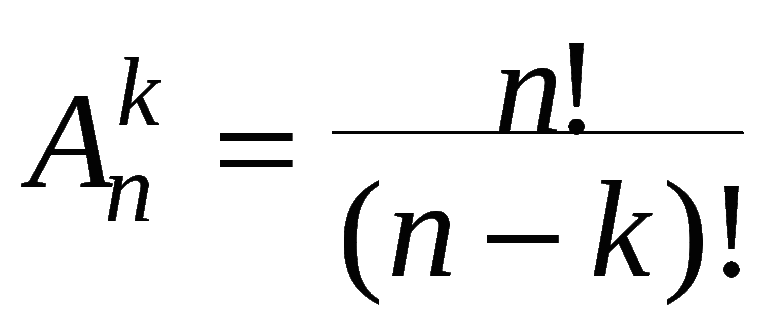Что такое число сочетаний

Число сочетаний

Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Явные формулы

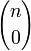
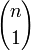
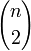
При фиксированном n производящей функцией последовательности чисел сочетаний , , , … является:

Двумерной производящей функцией чисел сочетаний является

Сочетания с повторениями

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.

Число сочетаний с повторениями из n по k равно биномиальному коэффициенту

При фиксированном значении n производящей функцией чисел сочетаний с повторениями из n по k является:

Двумерной производящей функцией чисел сочетаний с повторениями является:

Ссылки

Полезное

Смотреть что такое «Число сочетаний» в других словарях:

70 (число) — 70 семьдесят 67 · 68 · 69 · 70 · 71 · 72 · 73 40 · 50 · 60 · 70 · 80 · 90 · 100 Факторизация: 2×5×7 Римская запись: LXX Двоичное: 100 0110 … Википедия

ЭКСПОЗИЦИОННОЕ ЧИСЛО — световое число, условное число, однозначно выражающее внеш. условия при фотосъёмке (обычно яркость объекта съёмки и светочувствительность применяемого фотоматериала). Любому значению Э. ч. можно подобрать неск. сочетаний диафрагменное число… … Большой энциклопедический политехнический словарь

двойственное число — Форма числа, выделяющая два предмета как по отношению к единичному предмету, так и по отношению к множеству предметов. В современном русском языке эта форма не существует, но остатки ее влияния сохранились. Так, сочетания два стола (ср. мн. ч.… … Словарь лингвистических терминов

КОМБИНАТОРНЫЙ АНАЛИЗ — комбинаторная математика, комбинаторика, раздел математики, посвященный решению задач выбора и расположения элементов нек рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения… … Математическая энциклопедия

Сочетание — В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания… … Википедия

ВЕРОЯТНОСТЕЙ ТЕОРИЯ — занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера

Комбинаторика — 1) то же, что математический Комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов… … Большая советская энциклопедия

ПАРАДОКС — (греч. paradoxos неожиданный, странный) в широком смысле: утверждение, резко расходящееся с общепринятым, устоявшимся мнением, отрицание того, что представляется «безусловно правильным»; в более узком смысле два противоположных утверждения, для… … Философская энциклопедия

Формула включений-исключений — (или принцип включений исключений) комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом … Википедия

Комбинаторный анализ — математическая теория, занимающаяся определением числа различных способов распределения данных предметов в известном порядке; имеет особенно важное значение в теории уравнений и в теории вероятностей. Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Что такое число сочетаний

Таким образом, полученные комбинации удовлетворяют различным условиям.

В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.

Предварительно познакомимся с понятием факториала.

Произведение всех натуральных чисел от 1 до n включительно называют

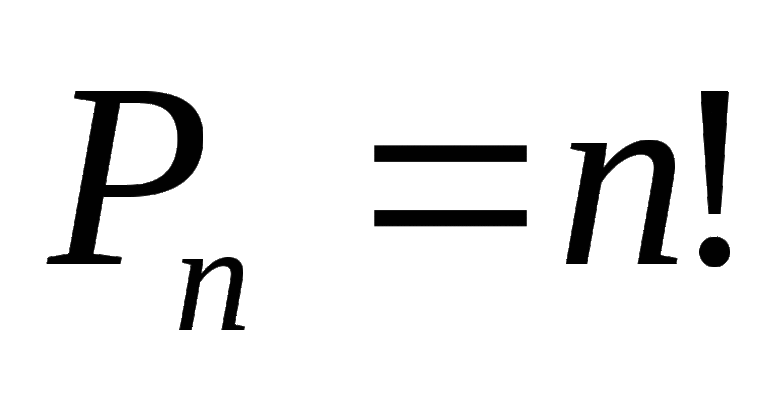
Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.

Число перестановок можно вычислить по формуле

Запишем эту формулу в факториальной форме:

Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:

Источник

Сочетания и размещения — что это такое и в чем разница

Оба этих понятия – сочетание и размещение – относятся к науке комбинаторике. Это раздел математики, созданный учеными Б. Паскалем и П. Ферма в процессе исследования теории карточных игр. Комбинаторика используется в решении задач особенного рода: когда требуется вычислить количество потенциальных вариантов для какой-либо ситуации. Примером может служить подсчет возможных позиций на шахматной доске после первого хода «черных» и «белых».

О сочетании и размещении говорят, когда из множества необходимо выбрать какое-либо подмножество. Понятия эти весьма близки по своему смыслу, поэтому так трудно бывает понять разницу между ними. Но она существует (причем принципиальная!). Ниже об этом достаточно простым языком написано в статье.

Сочетания

Сочетание – это подмножество, состоящее из К элементов, выбранных из множества, включающего в себя N элементов. При этом выполняется такое условие: N > К.

Важный момент: порядок расположения в данной выборке никакого значение не имеет. То есть комбинации, отличающиеся порядком размещения элементов, но не составом, считаются одинаковыми сочетаниями.

Образно проиллюстрировать понятие можно на примере лотереи. Предположим, человеку предлагается угадать 3 выпавшие цифры из 15-ти. Он выбрал следующий набор – 1, 6, 10. И уже не важно, в каком порядке они выпадут: 1, 6, 10; 1, 10, 6; 10, 1, 6; 10, 6, 1; 6, 10, 1; 6, 1, 10. Главное – состав комбинации. Если он совпадает с загаданным накануне набором цифр, игрок считается победителем.

Сочетания обозначаются следующим образом: С К _N. Где N – количество элементов в множестве, а К – количество объектов в производимой выборке. Для нашего примера N = 15, а К = 3.

Существует формула для определения числа возможных сочетаний в множестве. Выглядит она так: N!/((N-K)!*K!) подставим цифры из нашего примера:

Это означает, что из 15 чисел можно составить 455 различных комбинаций, включающих в себя три разных числа.

Такие подсчеты в нашем примере позволяют определить велики ли шансы субъекта на выигрыш.

Размещения

В самом названии этого термина присутствует корень, позволяющий понять его суть. Размещение – тоже подмножество, выбранное из первоначального множества. Но здесь уже существенное значение имеет место расположения элемента в комбинации. То есть если сочетания могут различаться только составом объектов, то размещения разнятся и составом, и порядком следования элементов.

Получается, что количество размещений всегда превосходит число сочетаний, при условии выборки из одного и того же множества.

Это легко проследить, если сделать выборку трех элементов из множества, состоящего всего из 4 объектов (от 1-го до 4-х).

Сочетаний здесь будет всего 4 (это легко проверить и по приведенной выше формуле):

Размещений же окажется гораздо больше:

123, 132, 321, 312, 231, 213, 234, 243, 324, 342 и т.д.

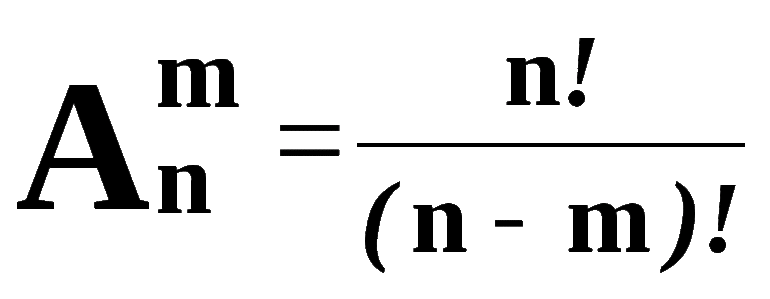
Существует формула, позволяющая подсчитать возможное количество размещений в представленном множестве:

Для нашего примера посчитаем количество потенциальных размещений:

Получается, что для состоящего из 4-х элементов множества существует 4 сочетания и целых 24 размещения.

Для тех, кто увлекается спортивными ставками, эти знания могут пригодится для того, чтобы рассчитать шансы на выигрыш.

Например, в турнире участвует 6 команд. Необходимо определить количество возможных комбинаций троек призеров кубка.

Обозначим названия команд буквами: А, Б, В, Г, Д, Е.

Сначала определим команду, которая станет золотым призером чемпионата. Таких вариантов, очевидно, 6: А, Б, В, Г, Д, Е.

Затем выбираем один из вариантов (пусть это будет комбинация, в которой золото принадлежит команде А), и определяем для него потенциального серебряного призера. Таких комбинаций уже окажется всего 5, так как одна команда уже записана на 1-м месте: АБ, АВ, АГ, АД, АЕ.

Такую пятерку вариаций можно сформировать для каждой из команд. То есть всего претендентов на серебро оказывается 30 (5*6).

Для каждой двойки первых призеров (чемпион-серебряный призер) можно составить только 4 комбинации с бронзовым призером. Первые два места уже распределены, так что остается 4 команды (6-2). Подберем комбинации для варианта АБ: АБВ, АБГ, АБД, АБЕ.

Мы уже подсчитали выше количество возможных комбинаций для первых двух мест – их оказалось 30. Теперь это число умножаем на 4 – получаем 120.

Выходит, что если в турнире участвует 6 команд, вариантов их размещения по первым трем местам может быть целых 120. Угадать призеров не так просто.

Сочетания и размещения: в чем же разница?

И сочетания, и размещения являются выборкой из определённого множества. Принципиальная разница между понятиями заключается лишь в том, что в случае сочетаний порядок расположения элементов не имеет значения, а в случае размещений он важен. Именно поэтому в пределах одного и того же множества количество сочетаний всегда оказывается меньше числа размещений.

Источник

Краткое описание

Изучение математических правил не может обойти стороной число сочетаний из n по k. Формулы комбинаторики как науки активно используются во всех жизненных отраслях. Этот раздел включён в школьную программу старших классов и вступительные испытания многих вузов России. Удивительная комбинаторика лежит в основе прикладного искусства.

Это направление науки начало активно развиваться ещё шесть веков назад. Достоверно известно, что первые комбинаторные задачи присутствовали в трудах философов и талантливых математиков Средневековья. В те времена представители стремительно развивающегося научного мира всячески пытались найти актуальные методы решения поставленных задач, хотели определить основные правила и понятия, а также утвердить уникальные в своём роде формулы и математические уравнения для тех, кто ещё не знаком с этим научным направлением.

Актуальные формулы и нормы комбинаторики применяются в распространённой теории вероятностей, где специалисты могут быстро и качественно подсчитать процент случайных событий, чтобы в итоге получить закон реального распределения случайных величин. При правильном подходе можно углублённо изучать закономерности тех или иных событий, что очень важно для понимания статистических природных правил, которые неизбежно проявляются в окружающей природе и эксплуатируемой технике.

Ключевые нюансы

Используемое в математике число сочетаний с повторениями можно подробно изучить по книгам и специальным изданиям. Комбинаторика подробно описана в том разделе науки, который занимается многофункциональными операциями с множеством задействованных элементов.

Экспертами было доказано, что это направление затрагивает довольно большой математический пласт, в котором ученикам предлагается изучить, сколько в мире существует различных комбинаций, подчиняющихся определённым условиям. Основной задачей этой науки можно считать требование размещения различных объектов по специальным правилам и последующее нахождение точного количества способов таких расположений.

На просторах интернета можно встретить много различных учебников и другого познавательного материала по информатике/математике для школьников, а также специальные сборники уравнений и сложных примеров для студентов, где в доступном и максимально подробном виде объяснена довольно увлекательная и познавательная комбинаторика. В начальных классах задачи на эту тему решают на специальных кружках, а вот в гимназиях с углублённым изучением точных наук ей посвящают основные уроки. Многоуровневые задачи по комбинаторике включены в программу олимпиады.

Существует ряд базовых понятий, которые нужно усвоить учащимся:

Необходимо отметить тот факт, что за основу может быть взят объект или целое явление, которое попадает в искомое множество. Перестановка затрагивает элементы, которые находятся в большом количестве и определённом порядке. Сочетание — своеобразные подмножества, пребывающие в произвольной форме. Размещение представляет собой упорядоченные подмножества в исходном множестве. Правильно посчитать нужный коэффициент можно при помощи многофункциональных онлайн-калькуляторов, которые обладают всеми необходимыми функциями.

Выборки и подсчёт суммы

Если предположить, что А = — множество из n элементов, то их совокупность будет называться выборкой объёма k из n. В этом случае действует ряд важных правил. Выборка может считаться правильно упорядоченной только в том случае, если итоговая последовательность следования всех задействованных элементов в ней была задана учеником заранее. Исключений не предусмотрено.

Различными выборками называются только те математические примеры, которые отличаются исключительно порядком следования элементов. Если отличия незначительные, тогда ученику предстоит работать с неупорядоченной комбинацией. В отдельных примерах могут допускаться или не должны допускаться повторения задействованных элементов.

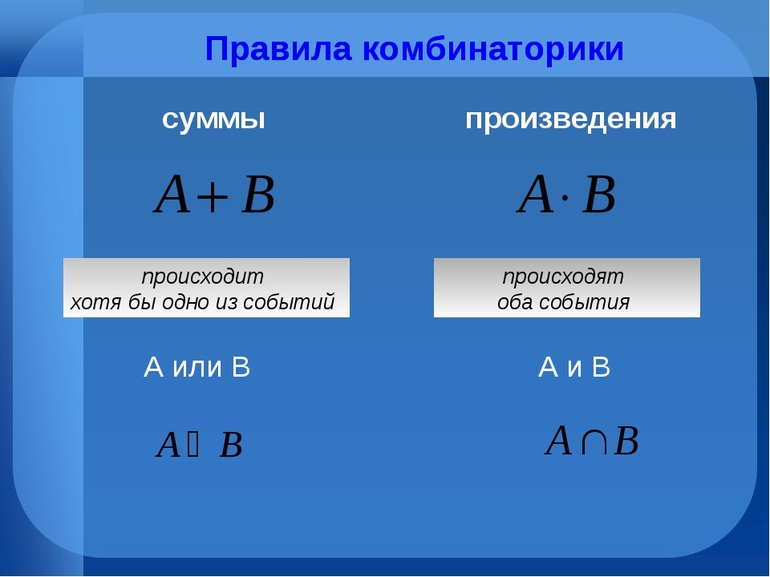
Чаще всего перед учащимися возникает необходимость подсчёта точного числа вероятных выборок с определёнными математическими параметрами. Довольно часто для контроля над вероятными комбинаторными объектами используется два ключевых приёма — правила произведения и суммы. На каждый случай специалисты предусмотрели ряд важных правил, которые призваны обезопасить учащегося от различных ошибок.

Базовое требование математического произведения основано на том, что когда исследуемый объект А может быть выбран различными f способами, то итоговый выбор А и B в указанном ранее порядке может быть осуществлён f * n методами. Правило суммы отличается тем, что если ученик имеет несколько возможностей выбрать точку А, тогда поиск А или В можно будет осуществить по специальной системе f + n.

Действующее правило произведения

Именно это направление в комбинаторике является одним из базовых для решения поставленных задач. При тщательном выборе элемента А из n способов (В из m) правильным считается то утверждение, в соответствии с которым одновременно подобрать пару А и В можно n * m методами, что очень важно. На этот случай действует три основных утверждения:

В эффективности описанных правил можно убедиться, благодаря некоторым примерам. По условиям задачи дано два ромба, три мяча, четыре гантели и пять кубов. Ученику нужно определить, сколькими способами можно будет вытянуть ромб, мяч, гантель и куб. Решение элементарное: 2*3*4*5= 120. Стоит отметить, что в этой задаче может быть задействован факториал, с помощью которого всегда можно вычислить более сложные варианты и решить трудные задачи.

По условиям следующего примера дано два мяча и пять скакалок. Задача состоит в том, чтобы определить, какова вероятность достать 1 скакалку и 1 мяч. Решение: 2*5=10.

Решение примеров комбинированного типа

Если ученик разобрался с основными свойствами сочетаний, то он также должен изучить уравнения всех доступных разновидностей задач с наиболее подходящими методами поиска правильных ответов. Эксперты рекомендуют потренироваться на более запутанных ситуациях, которые встречаются в повседневной жизни каждого человека. Основные категории задач:

Экспертами неоднократно было подтверждено, что комбинаторика является интересной и познавательной наукой, так как в наш век быстрой модернизации инновационных технологий постоянно будут нужны профессиональные специалисты, которые способны в полном объёме предоставить разнообразные решения для тех или иных практических задач.

Доступные размещения с повторениями и без них

Изучаемое число сочетаний без повторений сопряжено с некоторыми дополнительными нюансами. В этом случае в распоряжении учащегося имеется n разных математических элементов. Многих в такой ситуации интересует, сколько именно можно будет составить актуальных k расстановок.

Два базовых подхода считаются различными только при условии, если они отличаются друг от друга минимум одним элементом или состоят из аналогичных элементов, которые расположены в разном порядке. Каждый нюанс должен быть учтён, так как от этого зависит итоговый результат.

Источник

Количество сочетаний

Содержание:

Сочетания (выборки)

При работе с перестановками мы рассматривали различные способы размещения некоторого количества неких элементов друг относительно друга. Теперь мы займемся иной проблемой. Имеется некоторое количество п неких элементов, и надо рассмотреть различные способы, какими можно выбрать из них т элементов (0

Задача 1.

Ученику дано задание прочитать за лето любые две книги из указанных в списке четырех книг. Сколько у него есть способов выполнить это задание?

Решение:

Пусть в списке находятся книги А, Б. В, Г (обозначим так эти книги). Ученику надо прочитать любые из них, причем порядок прочтения не оговаривается. Допустим, в качестве первой он выбрал для чтения книгу А. Тогда, чтобы выполнить задание, ученик должен прочитать книги А, Б или А. В или А, Г. Если в качестве первой он выбрал книгу Б. то ему придется прочитать Б. В или Б, Г (вариант />, А совпадает с уже учтенным вариантом А, Б). Если в качестве первой ученик выбрал книгу В. то теперь у него остался один способ выполнить задание — прочитать В. Г. Вот и все возможные варианты:

А, Б; А, В; А, Г; Б, В; Б, Г; В, Г.

Этих вариантов шесть. Таким образом

По этой ссылке вы найдёте полный курс лекций по теории вероятности:

Задача 2.

Человеку нужно приобрести три подарка. В магазине ему предложили на выбор пять вполне равноценных предметов. Сколькими способами человек может сделать выбор?

Решение:

Обозначим предложенные предметы: А, Б, В. Г, Д. Возможные выборки грех из пяти (сочетания из пяти по три): А, Б, В\ А, Б, Г, А, Б. Д; А, В. Г; А. В. Д; А, Г, Д; Б, А. Г; Б. В. Д\ Б, Г, Д\ В, Г, Д. Всего 10 выборок. Таким образом,

Задача 3.

Решение:

Обозначим желающих получить путевку: А, Б, В. Г, Д, Е. Возможные способы выбрать троих из них:

Всего 20 способов. Таким образом,

Возможно вам будут полезны данные страницы:

Задача 4.

Сколькими способами можно выбрать из шести человек комиссию, состоящую из четырех членов?

Решение:

Обозначим шестерых претендентов: А, Б, В. Г. Д, Е.

Возможные выборки четырех из них:

Всего 15 выборок. Таким образом,

Если внимательно прочитать решения рассмотренных задач, то вполне можно уловить логику отбора нужных сочетаний, а значит, и подсчета их числа. Однако для большей наглядности обратимся, как и в случае с перестановками, к модели раскладывания шариков по отделениям в коробке. Правда, модель с шариками будет теперь иной. Раньше (при рассмотрении перестановок) число шариков равнялось числу отделений и принимался во внимание порядок расположения шариков друг по отношению к другу (недаром шарики различались, например, но цвету или номеру). Теперь число шариков меньше числа отделений (в частном случае оно равно числу отделений или нулю) и при этом порядок расположения шариков не учитывается (все шарики белые). Будем выяснять, сколькими способами можно разместить т одинаковых шариков по п отделениям, полагая, как и раньше, что в отделении может поместиться только один шарик. Число этих способов и есть число сочетаний из п элементов по т, или, иначе говоря, число выборок т элементов из п.

Возможен вопрос: если речь идет о разных размещениях т шариков по п отделениям, то о какой выборке тут можно говорить? Из чего и что именно мы здесь выбираем? И что здесь понимается под словом «элемент»? Отвечаем: из общего числа п отделений мы выбираем здесь т занятых шариками отделений.

Отделение занято — значит, в него положен шарик. В роли элементов выступают здесь отделения, причем порядок выбранных (занятых) отделений не учитывается.

Начнем с двух частных случаев. Первый: . Ситуация, когда ни водно из отделений не положен шарик, разумеется, возможна. Но возможны ли два или более разных способов нс положить ни одного шарика ни в одно отделение? — Нет, невозможны. Значит, есть только один способ реализовать данную ситуацию; следовательно,

Второй частный случай: Это значит, что в каждом отделении есть по шарику. Реализовать такую ситуацию можно тоже только одним способом (ведь шарики одинаковы и, значит, порядок их размещения учитывается). Следовательно,

Далее обратимся к случаям, когда. Сколькими способами можно разместить один шарик в коробке с п отделениями? Очевидно, таких способов п (надо поочередно помещать шарик в каждое из п отделений). Следовательно,

Для соответствующие способы размещения шарика изображены на рис. 1,а в таблице 16.

А на рис. 1,6 в той же таблице показаны случаи, когда (опять-таки для ). Мы видим, что

И эго отнюдь нс случайное совпадение! Есть определенная аналогия между рис. 1, а и рис. 1, б. На рис. 1, а в каждом размещении участвует один шарик, или, иными словами, одно занятое отделение, а на рис. 1, б в каждом размещении участвует одно незанятое (пустующее) отделение. Понятно, что число способов, какими из п отделений можно выбрать

Соотношение (1) можно обобщить для любого :

На рис. 2 в таблице 16 наглядно демонстрируется справедливость формулы (6) для случая, когда . Размещать три шарика по пяти отделениям — это все равно, что размещать по пяти отделениям два пустых места. А размешать два пустых места — это все равно, что размешать два шарика.

Задача 5.

Сколькими способами можно разбить группу из п человек на две подгруппы, в одной из которых будет т человек, а в другой ?

Задача имеет два решения.

Решение первое. Надо выяснить, сколькими способами можно выбрать m человек из n. Понятно, что число таких способов равно . При этом всякий раз автоматически выявляется и соответствующая подгруппа, состоящая из человек.

Решение второе. Надо выяснить, сколькими способами можно выбрать человек из n. Число таких способов равно . При этом всякий раз выявляется и подгруппа из m человек.

Оба решения дают ответ на вопрос, поставленный в задаче. А это как раз и означает, что

Эти рассуждения поясняет рис. 3 из таблицы 16.

Задача 6.

Используя соотношение (7), надо найти, чему равно

Решение:

Согласно (7), . Из задачи 4 мы знаем, что Далее учтем, что . Таким образом,

Задача 7.

Используя (7), надо найти, чему равно С^.

Решение:

Согласно (7), Мы уже знаем, что и, значит, . Что же касается то применим еще раз соотношение (7);

Задача 8.

Используя (7), надо найти, чему равно

Решение:

Согласно (7), мы уже подсчитывали (в задаче 6) и получили 21. Нам известно также , оно равно 35 (см. задачу 7). Таким образом,

Формула для подсчета числа сочетаний

Полезность соотношения (7) очевидна. Однако вряд ли удобно пользоваться им всякий раз, как потребуется найти число тех или иных выборок. Хотелось бы иметь формулу, позволяющую сразу подсчитать коль скоро даны

Отсюда следует искомая формула:

Возникает вопрос: как быть, если Тут можно поступить двояко. Можно оговорить, что формула (8) применима для и и учитывать, что. А можно условиться, что 0! = 1,

и пользоваться формулой (8) во всех случаях. Математики предпочитают использовать второй вариант.

Рассмотрим несколько задач с использованием формулы (8).

Задача 9.

Решение:

Число способов равно . Используя (8), находим:

Задача 10.

Дзя подарков ко дню восьмого марта человек должен приобрести три броши и три браслета. В магазине ему предложили на выбор пять брошей и шесть браслетов. Сколькими способами человек может сделать выбор?

Решение:

Три броши из пяти можно выбрать числом способов, равным , а три браслета из шести — числом способов . Каждый из способов выбора броши нужно скомбинировать с каждым из способов выбора браслета. Следовательно, полное число способов, какими человек может выбрать три броши и три браслета, есть

Задача 11.

Восемь человек должны расположиться в двух комнатах, причем так. чтобы в каждой бы.ю не менее трех человек. Сколькими способами это можно сделать?

Решение:

Есть два варианта. Первый: в одной комнате три человека, а в другой пять. Второй: в каждой комнате по четыре человека. В первом варианте число способов размещения равно числу выборок трех из восьми (или пяти из восьми, что одно и то же); это число есть . Во втором варианте число способов размещения равно числу выборок четырех из восьми, т. е. равно . Полное число способов размещения людей должно учитывать как первый, так и второй варианты:

Задача 12.

Группу из девяти человек надо разбить на три подгруппы — в одной два человека, в другой три, в третьей четыре. Сколькими способами можно выполнить такое разбиение?

Решение:

Сначала выясняем, сколькими способами можно выбрать двух человек из девяти. Это число способов равно . После того, как этот выбор состоялся, осталось семь человек. Из них надо организовать подгруппы из трех и четырех человек. Это можно сделать числом способов, равным (или , что одно и то же). Итак, девять человек можно разбить на два, три и четыре следующим числом способов:

Примечание. Можно было бы сначала выяснить, сколько есть выборок трех человек из девяти. Тогда ответ на вопрос задачи дало бы произведение . А можно было бы сначала выяснить, сколько есть выборок четырех человек из девяти. Тогда ответ дало бы произведение Предлагаем самостоятельно убедиться, что

Задача 13.

Сколькими способами можно рассадить за столом пять гостей, если стол накрыт на семь персон?

Решение:

Пять выборок из семи равно . Но это еще не ответ на поставленный в задаче вопрос, поскольку при рассаживании гостей за столом необходимо принимать во внимание также число перестановок пяти гостей (оно равно П₅). Ведь занявших те или иные пять стульев можно поменять местами. Таким образом, пять гостей можно рассадить за столом, накрытым на семь персон, числом способов, равным

Лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник