Что такое численность конечного множества
Конечное множество
Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным.
Содержание
Формальное определение
Два множества 
и 
называются эквивалентными, если существует биективное отображение одного множества в другое. Если множества X и Y эквивалентны, то этот факт записывают 
или 
и говорят, что множества имеют одинаковые мощности.
Множество 
называется конечным, если оно эквивалентно множеству 
при некотором неотрицательном целом 
. При этом число называется количеством элементов множества , что записывается как 
. [1]
В частности, пустое множество является конечным множеством, количество элементов которого равно 0, то есть, 
.
Свойства
См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Конечное множество» в других словарях:
конечное множество — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN finite set … Справочник технического переводчика
МНОЖЕСТВО — МНОЖЕСТВО, множества, ср. (книжн.). 1. только ед. Неопределенно большое количество, число чего нибудь. Множество рабочих. Множество фактов. «Я слышал в жизни множество отличнейших певцов.» Некрасов. 2. Совокупность элементов, выделенных в… … Толковый словарь Ушакова
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия
Конечное — то, что имеет предел, границу, конец. В философии понятие К. используется как категория, характеризующая всякий определённый, ограниченный объект (вещь, процесс, явление, состояние, свойство и т. д.). Каждый познаваемый объект… … Большая советская энциклопедия
Разрешимое множество — В теории множеств, теории алгоритмов и математической логике, множество натуральных чисел называется разрешимым или рекурсивным, если существует алгоритм, который, получив на вход любое натуральное число, через конечное число шагов завершается и… … Википедия
Дескриптивное множество — Дескриптивное множество конечное множество, каждому элементу которого поставлено в соответствие неотрицательное число («вес»)[1]. В случае фиксированного для определённого исследования элементов дескриптивного множества, можно использовать… … Википедия
Перечислимое множество — Не следует путать с счётным множеством. В теории множеств, теории алгоритмов и математической логике, перечислимое множество (эффективно перечислимое, рекурсивно перечислимое, полуразрешимое множество[1]) множество конструктивных объектов… … Википедия
Арифметическое множество — В теории множеств и математической логике, множество натуральных чисел называется арифметическим, если оно может быть определено формулой в языке арифметики первого порядка, то есть если существует такая формула с одной свободной переменной что… … Википедия
Число элементов объединения и разности двух конечных множеств
Урок 1,2 ТЕОРИЯ МНОЖЕСТВ
Множество – это совокупность объектов (в математике или окружающей действительности), сгруппированных по какому-либо признаку.
Обозначают множество заглавной латинской буквой, например, множество А, множество В.
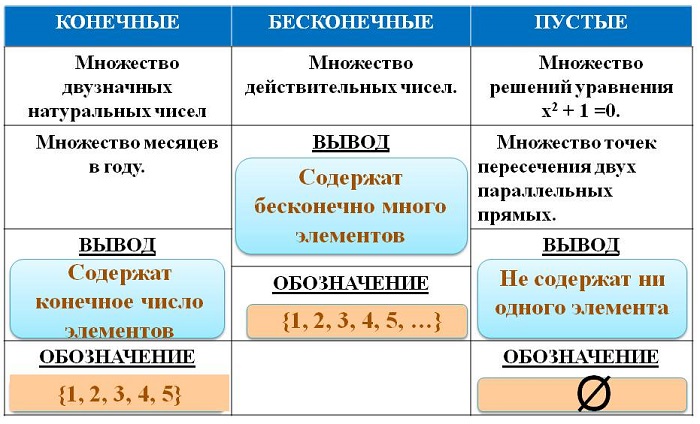
Множество – не значит «много». Множество может состоять из большого числа элементов, из нескольких элементов или из одного элемента. А так же множество может вообще не содержать ни одного элемента. Такое множество называют «пустое множество» и обозначают символом Ø
Элементы множества – это объекты или предметы, составляющие множество. Обозначают строчными латинскими буквами: a, b, c, d, t, f и т.д.
Множества бывают конечные и бесконечные. Например, множество всех двухзначных чисел – конечное. Множество всех целых чисел – бесконечное. Для некоторых числовых множеств в математике приняты стандартные обозначения:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
R – множество действительных чисел.
Способы задания множеств
1. Пересечением (применяется только для конечных множеств). Все элементы множества записывают в фигурных скобках.
Например, множество всех чётных однозначных чисел запишем так:
2. Характеристическими свойствами (когда элементов очень много или множество является бесконечным).
Например, множество В =
Зададим то же самое множество с помощью характеристических свойств:
а) б) в) г) д)
 |
Число элементов объединения и разности двух конечных множеств
Пусть A и B — конечные множества. Число элементов множества A условимся обозначать символом m(A) и называть численностью множества A.
Определим численность объединения множеств A и B.
Если множества A и B не пересекаются (см. рис. 1а), то m(AÈB) = m(A) + m(B). Таким образом, численность объединения конечных непересекающихся множеств равна сумме численностей этих множеств.
Определим теперь численность разности множеств A и B.
Если множества A и B не пересекаются (см. рис. 1а), то A \ B = A, и поэтому m(A\B) = m(A).
Примеры решения задач
Задача 1. Каждый студент первого курса обязан изучать хотя бы один иностранный язык. На юридическом факультете изучаются либо английский, либо немецкий язык. Из 94 первокурсников юридического факультета 76 человек изучают английский язык, 34 – изучают немецкий. Сколько студентов изучают два языка?
Решение. Обозначим А – множество студентов, изучающих английский язык; В – множество студентов, изучающих немецкий язык. Множество всех первокурсников равно АÈВ. Множество, изучающих два языка AÇB. Воспользуемся формулой
Из условия задачи m(A)=76, m(B)=34, m(AÈB) =94. Поэтому
Дата добавления: 2020-11-23 ; просмотров: 308 ; Мы поможем в написании вашей работы!
Значение словосочетания «конечное множество»
конечное множество из пяти элементов. Число элементов конечного множества является натуральным числом и называется мощностью множества. Множество всех положительных целых чисел бесконечно:
Конечные множества играют особую роль в комбинаторике, которая изучает дискретные объекты. Рассуждения о конечных множествах используют принцип Дирихле, согласно которому не может существовать инъекция из большего конечного множества в меньшее.
конечное множество
2. матем. множество, для которого существует неотрицательное целое число, равное количеству элементов этого множества
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова торчок (существительное):
Ассоциации к слову «конечный»
Ассоциации к слову «множество»
Синонимы к словосочетанию «конечное множество»
Предложения со словосочетанием «конечное множество»
Цитаты из русской классики со словосочетанием «конечное множество»
Сочетаемость слова «конечный»
Сочетаемость слова «множество»
Понятия, связанные со словосочетанием «конечное множество»
В математике, симметрической алгеброй S(V) (также обозначается Sym(V)) векторного пространства V над полем K называется свободная коммутативная ассоциативная K-алгебра с единицей, содержащая V.
Афоризмы русских писателей со словом «конечный»
Отправить комментарий
Дополнительно
Предложения со словосочетанием «конечное множество»
Можно только на свой вкус отобрать конечное множество разнообразных определений чисел, и в какой-то момент сказать себе стоп!
Каждый алфавит являет собой некоторое конечное множество элементов, которые соответствуют событиям представления информации для её передачи в том или ином виде (в пространстве, или во времени).
Однако настоятельно напомню, что «сгорая» в конечном множестве звёзд, материальные массы порождают не только лучевую энергию фотонного типа и космические лучи «звёздного ветра», но и те «лёгкие» кванты, которые образуют так называемый вакуум космического пространства.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.
Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками < >.
А = <а, в, с, у>– А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N =
Выделяют три вида множеств:
пустые (обозначаются Ø) – не имеющие элементов.
Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
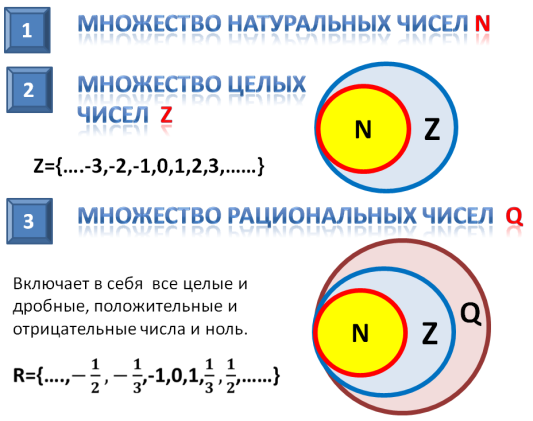
Множество натуральных чисел
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
Следовательно, N и Z являются подмножествами Q.
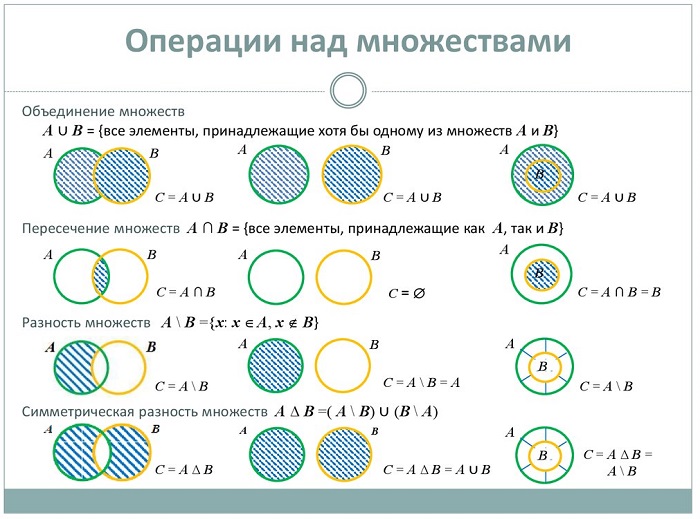
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Объединение
Пересечение
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:
Коммутативность – переместительные законы:
умножения S ∩ D = D ∩ S;
сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
если S ⊆ Fи F ⊆ J, то S ⊆ J;
если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
О других свойствах операций можно узнать из картинки:
Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
Множества: понятие, определение, примеры
Множеством называется собрание, совокупность, коллекция вещей, объединенных по какому-либо признаку или по какому-либо правилу. Понятие множества возникает путем абстракции. Рассматривая какую-либо совокупность предметов как множество, отвлекаются от всех связей и соотношений между различными предметами, составляющими множества, но сохраняют за предметами их индивидуальные черты. Таким образом, множество, состоящее из пяти монет, и множество, состоящее из пяти яблок, — это разные множества. С другой стороны, множество из пяти монет, расположенных по кругу, и множество из тех же монет, положенных одна на другую, — это одно и то же множество.
Приведем несколько примеров множеств. Можно говорить о множестве песчинок, составляющих кучу песка, о множестве всех планет нашей солнечной системы, о множестве всех людей, находящихся в данный момент в каком-либо доме, о множестве всех страниц этой книги. В математике тоже постоянно встречаются различные множества, например множество всех корней заданного уравнения, множество всех натуральных чисел, множество всех точек на прямой и т. д.
Математическая дисциплина, изучающая общие свойства множеств, т. е. свойства множеств, не зависящие от природы составляющих их предметов, называется теорией множеств. Эта дисциплина начала бурно развиваться в конце XIX и начале XX в. Основатель научной теории множеств — немецкий математик Г. Кантор.
Работы Кантора по теории множеств выросли из рассмотрения вопросов сходимости тригонометрических рядов. Это весьма обычное явление: очень часто рассмотрение конкретных математических задач ведет к построению весьма абстрактных и общих теорий. Значение таких абстрактных построений определяется тем, что они оказываются связанными не только с той конкретной задачей, из которой они выросли, но имеют приложения и в ряде других вопросов. В частности, именно так обстоит дело и с теорией множеств. Идеи и понятия теории множеств проникли буквально во все разделы математики и существенно изменили ее лицо. Поэтому нельзя получить правильного представления о современной математике, не познакомившись с элементами теории множеств. Особенно большое значение имеет теория множеств для теории функций действительного переменного.
Множество считается заданным, если относительно любого предмета можно сказать, принадлежит он множеству или не принадлежит. Иными словами, множество вполне определяется заданием всех принадлежащих ему предметов. Если множество \(M\) состоит из предметов \(a,\,b,\,c,\,\ldots\) и только из этих предметов, то пишут
Объединение или сумма множеств
При этом, даже если элемент \(x\) принадлежит нескольким слагаемым, то он входит в сумму \(M\) лишь один раз. Ясно, что
Пересечение множеств
Читателю рекомендуется доказать, что сумма и пересечение множеств связаны обычным распределительным законом
Разность множеств
Нетрудно показать, что всегда
Таким образом, правила действий над множествами значительно отличаются от обычных правил арифметики.
Конечные и бесконечные множества
Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то такое множество называется бесконечным. Например, множество всех натуральных чисел бесконечно.
Рассмотрим два каких-либо множества \(M\) и \(N\) и поставим вопрос о том, одинаково или нет количество элементов в этих множествах.
Однако, если оба множества \(M\) и \(N\) бесконечны, то путь простого счета элементов ничего не дает. Поэтому сразу возникают такие вопросы: все ли бесконечные множества имеют одинаковое количество элементов, или же существуют бесконечные множества с большим и меньшим количеством элементов? Если верно второе, то каким способом можно сравнивать между собой количество элементов в бесконечных множествах? Этими вопросами мы теперь и займемся.
Взаимно однозначное соответствие множеств
Пусть в зале находится некоторое число людей и некоторое число стульев. Чтобы узнать, чего больше, достаточно попросить людей занять места. Если кто-нибудь остался без места, значит, людей больше, а если, скажем, все сидят и заняты все места, то людей столько же, сколько стульев. Описанный способ сравнения количества элементов во множествах имеет то преимущество перед непосредственным счетом элементов, что он без особых изменений применяется не только к конечным, но и к бесконечным множествам.
Рассмотрим множество всех натуральных чисел
Какое множество содержит больше элементов? На первый взгляд кажется, что первое. Однако мы можем образовать из элементов этих множеств пары, как указано ниже.
Ни один элемент \(M\) и ни один элемент \(N\) не остается без пары. Правда, мы могли бы также образовать пары и так:
Тогда многие элементы из \(M\) остаются без пар. С другой стороны, мы могли бы составить пары и так:
Таким образом, мы получили ответ на один из поставленных выше вопросов: как сравнивать между собой количество элементов в бесконечных множествах. Однако это нисколько не приблизило нас к ответу на другой вопрос: существуют ли вообще бесконечные множества. имеющие различные мощности? Чтобы получить ответ на этот вопрос, исследуем некоторые простейшие типы бесконечных множеств.
Счетные множества. Если можно установить взаимно однозначное соответствие между элементами множества \(A\) и элементами множества всех натуральных чисел
Таблица 1 показывает, что множество всех четных чисел счетно (верхнее число рассматривается теперь как номер соответствующего нижнего числа).
Счетные множества это, так сказать, самые маленькие из бесконечных множеств: во всяком бесконечном множестве содержится счетное подмножество.
Если два непустых конечных множества не пересекаются, то их сумма содержит больше элементов, чем каждое из слагаемых. Для бесконечных множеств это правило может и не выполняться. В самом деле, пусть \(G\) есть множество всех четных чисел, \(H\) — множество всех нечетных чисел и \(Z\) — множество всех натуральных чисел. Как показывает таблица 4, множества \(G\) и \(H\) счетны. Однако множество \(Z=G+H\) вновь счетно.
Нарушение правила «целое больше части» для бесконечных множеств показывает, что свойства бесконечных множеств качественно отличны от свойств конечных множеств. Переход от конечного к бесконечному сопровождается в полном согласии с известным положением диалектики — качественным изменением свойств.
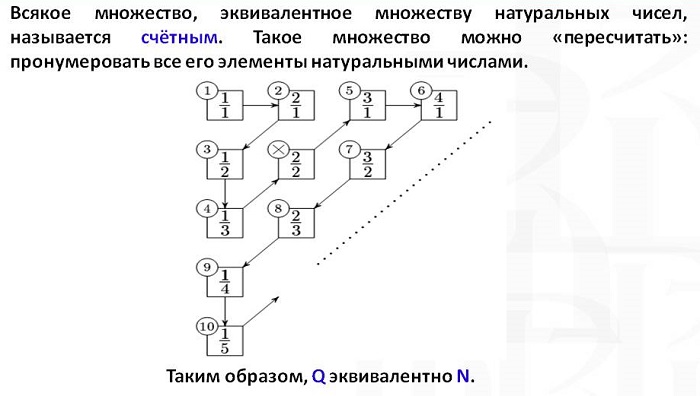
Здесь в первой строке помещены все натуральные числа в порядке их возрастания, во второй строке 0 и целые отрицательные числа в порядке их убывания, в третьей строке — положительные несократимые дроби со знаменателем 2 в порядке их возрастания, в четвертой строке — отрицательные несократимые дроби со знаменателем 2 в порядке их убывания и т. д. Ясно, что каждое рациональное число один и только один раз находится в этой таблице. Перенумеруем теперь
все числа этой таблицы в том порядке, как это указано стрелками. Тогда все рациональные числа разместятся в порядке одной последовательности:
Этим установлено взаимно однозначное соответствие между всеми рациональными числами и всеми натуральными числами. Поэтому множество всех рациональных чисел счетно.
Множества мощности континуума
Из рис. 1 видно, что множество точек любого отрезка \(AB\) имеет мощность континуума. Здесь взаимно однозначное соответствие устанавливается геометрически, посредством проектирования.
Нетрудно показать, что множества точек любого интервала \(x\in[a,b]\) и всей числовой прямой \(x\in[-\infty,+\infty]\) — имеют мощность континуума.
Значительно более интересен такой факт: множество точек квадрата \(0\leqslant x\leqslant1,\) \(0\leqslant y\leqslant1\) имеет мощность континуума. Таким образом, грубо говоря, в квадрате «столько же» точек, сколько и в отрезке.