какая вероятность считается высокой
Теория вероятностей для самых маленьких
Авторизуйтесь
Теория вероятностей для самых маленьких
директор по технологиям в «Синимекс Дата Лаб»
В этой статье мы рассмотрим основы статистики, полезные изучающим машинное обучение, а также желающим освежить свои знания. Понятия, о которых пойдет речь ниже, встречаются в очень разнообразных контекстах, а также лежат в основе всеми любимого data science. Всегда полезно повторить азы теории, так как зачастую это помогает открыть для себя что-то новое, на что раньше не обращали внимание. Поэтому, начнем.
Вероятности
Зачем нам нужны вероятности, когда мы обладаем таким мощным математическим инструментарием? У нас есть матанализ для работы с функциями на бесконечно малых величинах и оценки их динамики. У нас есть алгебра для решения уравнений, а также десятки других областей математики, с помощью которых мы можем решить едва ли не любую задачу.
Проблема в том, что мы живем в хаотичной вселенной, где точные измерения чаще всего невозможны. Изучая реальные процессы, происходящие в мире, мы хотим понять, какие случайные события влияют на наши эксперименты. Нас окружает неопределенность, и важно уметь «обуздать» и использовать ее в своих целях. Именно в такие моменты в ход идет теория вероятностей и статистика.
В наш век именно эти дисциплины лежат в основе искусственного интеллекта, физики элементарных частиц, обществознания, биоинформатики.
Перед тем как говорить о статистике, необходимо определиться с понятием вероятности. Как ни странно, однозначного ответа нет. Рассмотрим несколько теоретических подходов к определению вероятности.
Частотная вероятность
Представим, что нам дали монету, и мы хотим определить является ли она честной. Как это можно сделать? Подбросим ее несколько раз и запишем как 1, если выпадет орёл, 0 – если выпадет решка. Повторим этот эксперимент 1000 раз, и подсчитаем все 0 и 1. Допустим, по результатам этого утомительного процесса мы насчитали 600 орлов (1) и 400 решек (0). Если мы посчитаем частоту, с которой нам выпадал орёл или решка, мы получим 60% и 40%, соответственно. Эти частоты могут интерпретироваться как вероятности того, что, подбросив монету, нам выпадет орёл или решка. Такой подход к вероятностям называется частотным.
Условные вероятности
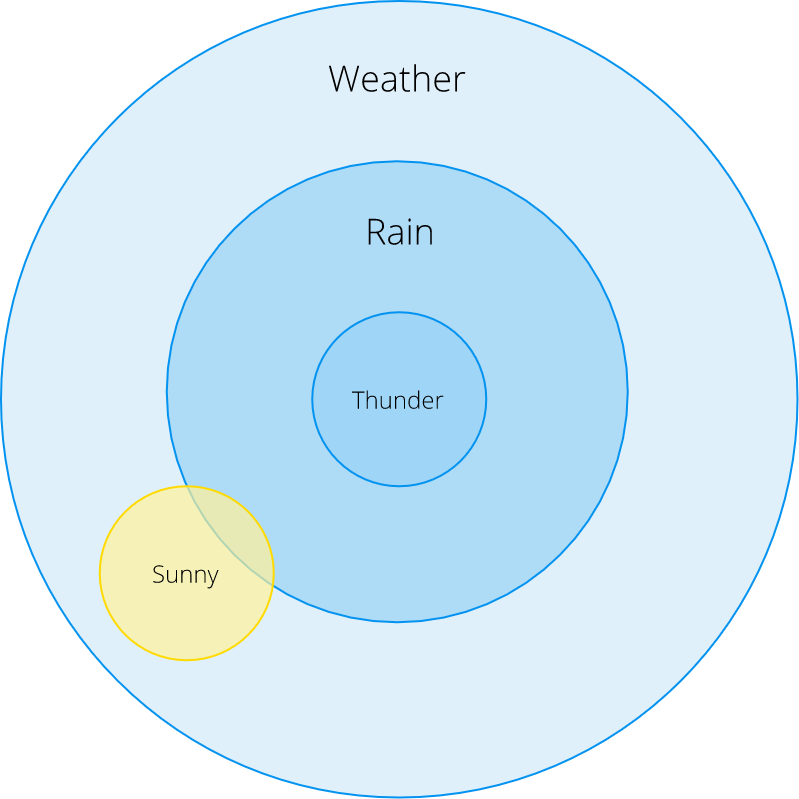
Зачастую нам нужно узнать вероятность наступления события при условии, что произошло другое событие. В этом случае, мы указываем условную вероятность события A при условии, что произошло событие B как P (A | B). Рассмотрим это на примере дождя:
Из этой диаграммы Эйлера мы видим, что P (Дождь | Гром) = 1: дождь идет всегда, когда мы слышим раскаты грома и видим молнии (в реальности это не всегда так, но примем условности для целей нашего примера).
А что насчет P (Дождь | Солнце)? На глаз, эта вероятность достаточно мала, но есть ли способ рассчитать ее точно? Условная вероятность определяется как:
Иными словами, мы должны поделить вероятность наступления обоих событий – Дождя и Солнечной погоды на вероятность события Солнечная погода.
Зависимые и независимые события
События называются независимыми, если вероятность наступления любого из них никак не зависит от наступления других событий. Например, рассмотрим вероятность того, чтобы бросить игральные кости и выкинуть две двойки подряд. Это независимые события. Иными словами,
Но почему эта формула работает? Для начала обозначим броски №1 и №2 как A и B, чтобы упростить формулу, а далее перепишем вероятность бросания костей как вероятность появления двух независимых событий:
Если формулу выше прочитать справа налево, мы увидим, что P (A | B) = P(A). По сути, это означает, что событие A не зависит от события B. Такая же логика справедлива и в отношении P(B).
Байесовский подход к вероятности
Существует еще один подход к определению вероятностей, который называется Байесовским. Частотный подход к статистике предполагает существование одной оптимальной и конкретной комбинации параметров для модели. Частотная статистика работает с неопределенностью через достаточно сложные для понимания доверительные интервалы (confidence interval). К примеру, 95% доверительный интервал в частотной статистике означает, что если бы мы проводили измерение бесконечное количество раз, то истинное значение параметра попадало бы в этот интервал в 95% случаев. Сбивает с толку, да?
С другой стороны, Байесовская теорема подходит к параметрам с вероятностных позиций и рассматривает их как случайные величины. В Байесовской статистике каждый параметр обладает собственным распределением вероятности, которое отражает, насколько вероятны данные параметры, учитывая имеющиеся в наличии данные. Математически это можно представить как:
В отличие от частотного подхода, Байесовская статистика работает с неопределенностью через достоверные интервалы (credible interval), которые интуитивно понятны. 95% достоверный интервал означает, что значение измеряемого параметра попадает в него с 95% вероятностью.
В этой ветке статистики все крутится вокруг теоремы, позволяющей рассчитать условные вероятности исходя из накопленных знаний:
Несмотря на кажущуюся простоту, Теорема Байеса имеет огромную ценность, она применяется в различных областях, и даже существует отдельная ветвь статистики, которая называется Байесовская статистика. Если интересно понять, как выводится эта формула, то вот ссылка на отличный пост, посвященный Теореме Байеса.
Распределения
Распределение вероятностей – это закон, описывающий вероятности наступления всех возможных исходов какой-либо случайной величины, выраженных в виде математической функции. Как и любая функция, распределение может обладать параметрами, позволяющими скорректировать его характеристики.
Когда мы измеряли относительную частоту исходов такого события как подбрасывание монеты, мы на самом деле рассчитали так называемое эмпирическое распределение вероятностей. Многие процессы, отличающиеся неопределенностью, могут быть описаны в терминах распределения вероятностей. Так, например, подбрасывание монеты описывается распределением Бернулли, а если бы мы захотели рассчитать вероятность, что после n попыток выпадет орел, мы можем прибегнуть к Биномиальному распределению.
Для удобства работы с вероятностями введем новое понятие, аналогичное переменной, — случайная переменная. Каждая случайная переменная соответствует определенному распределению. Случайные величины принято обозначать заглавной буквой, а также мы можем использовать символ
, чтобы обозначить, какому распределению соответствует переменная.
Это означает, что случайная переменная X описывается распределением Бернулли, при этом вероятность успеха (выпадение орла) равна 0,6.
Непрерывное и дискретное распределение вероятностей
Распределения вероятностей бывают двух типов. Дискретное распределение описывает случайные величины, которые принимают конечное число значений, как это было в примере с монетой и распределением Бернулли. Дискретные распределения определяются Функцией распределения масс (Probability Mass Function). Непрерывное распределение описывает непрерывные случайные величины, которые (в теории) могут принимать бесчисленное число значений. Например, когда мы измеряем скорость и ускорение датчиками с высокими шумами. Непрерывные распределения определяются Функцией плотности распределения вероятности (Probability Density Function).
При расчете статистик для дискретного распределения вероятностей применяется суммирование ∑, а для непрерывного – интегралы ∫. Например, математическое ожидание будет иметь следующий вид:
Выборки и статистики
Представим, что мы хотим измерить рост людей в своем городе. Чтобы измерения были независимыми, мы оценивали рост случайных прохожих на улице. Процесс случайного отбора подмножества данных из общей (генеральной) совокупности называется выборкой.
Выборка сама по себе достаточно сложна для понимания. Для того, чтобы описать ее более понятным для человека способом используются статистические показатели – обобщающие математические функции.
С одним таким показателем вы скорее всего уже сталкивались – это арифметическое среднее.
Другой пример – это дисперсия выборки:
Данная формула характеризует разброс значений в массиве данных относительно среднего.
А если я хочу узнать больше?
Знания статистики могут пригодиться в самых неочевидных ситуациях. Как сказал известный статист Джон Тьюки: «The best thing about being a statistician is that you get to play in everyone’s backyard».
Вот небольшая подборка ресурсов для продолжения изучения математической статистики:
Теория вероятности формулы и примеры решения задач
События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти. В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).
Зачем нужна теория вероятности
Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.
Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.
В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.
Основные понятия теории вероятности
Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.
События А и В называется несовместными, если они не могут произойти одновременно.
Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом 
Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом 
Важным частным случаем является ситуация, когда имеется 


Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов 

Ответ получаем по формуле 
Пример задачи из ЕГЭ по математике по определению вероятности
На столе лежат 20 пирожков — 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?
Решение.
Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть 
Независимые, противоположные и произвольные события
Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.
События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.
Событие B состоит в том, что событие А не произошло, т.е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е. 
Теоремы сложения и умножения вероятностей, формулы
Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е.
.
Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае 
Последние 2 утверждения называются теоремами сложения и умножения вероятностей.
Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.
Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение 
В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов 

Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение 
В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам
В нашем случае 
И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: 


В нашем случае 
Примеры решения задач из ЕГЭ по математике на определение вероятности
Задача 1. Из сборника под ред. Ященко.
На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.

Задача 2. Из сборника под ред. Ященко.
В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность того, что наугад взятая лампочка из партии будет исправной.
Решение: Количество исправных лампочек 1000-20=980. Тогда вероятность того, что взятая наугад лампочка из партии будет исправной:
Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.
Если мы вообразим числовую прямую и на ней отметим точки 8 и 9, то мы увидим, что условие «У. верно решит ровно 9 задач» входит в условие «У. верно решит больше 8 задач», но не относится к условию «У. верно решит больше 9 задач».
Однако, условие «У. верно решит больше 9 задач» содержится в условии «У. верно решит больше 8 задач». Таким образом, если мы обозначим события: «У. верно решит ровно 9 задач» — через А, «У. верно решит больше 8 задач» — через B, «У. верно решит больше 9 задач» через С. То решение будет выглядеть следующим образом:

На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Давайте подумаем какие у нас даны события. Нам даны два несовместных события. То есть либо вопрос будет относиться к теме «Тригонометрия», либо к теме «Внешние углы». По теореме вероятности вероятность несовместных событий равна сумме вероятностей каждого события, мы должны найти сумму вероятностей этих событий, то есть:
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Рассмотрим возможные события. У нас есть три лампочки, каждая из которых может перегореть или не перегореть независимо от любой другой лампочки. Это независимые события.
Тогда укажем варианты таких событий. Примем обозначения: 



Заметим, что благоприятных нам несовместных событий всего 7. Вероятность таких событий равна сумме вероятностей каждого из событий: 
Еще одну задачку вы можете посмотреть на рисунке:
Таким образом, мы с вами поняли, что такое теория вероятности формулы и примеры решения задач по которой вам могут встретиться в варианте ЕГЭ.
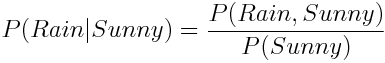
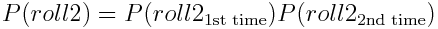
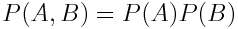
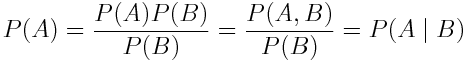

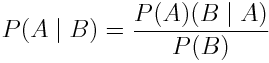

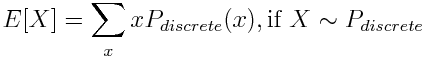
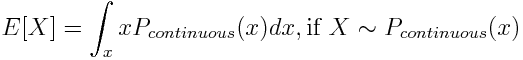
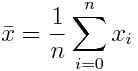
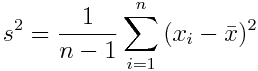



 .
.



















