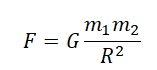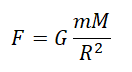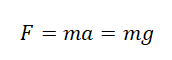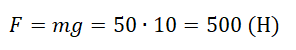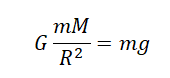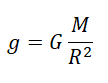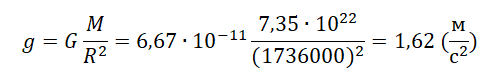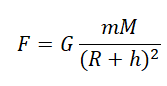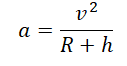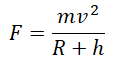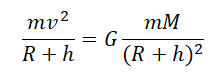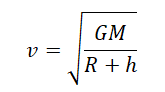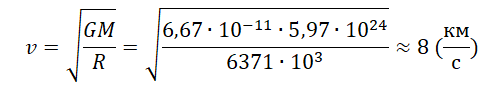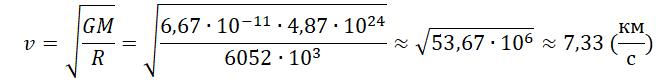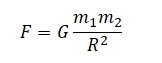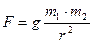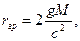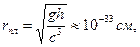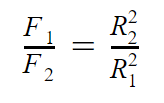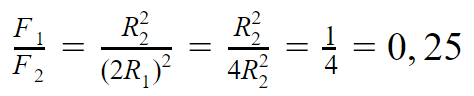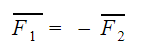какая величина является мерой гравитационного взаимодействия тел
Гравитационные силы. Закон всемирного тяготения.
теория по физике 🧲 динамика
Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготения
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
F — сила всемирного тяготения, m1 и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10 –11 Н ∙ м 2 /кг 2 ).
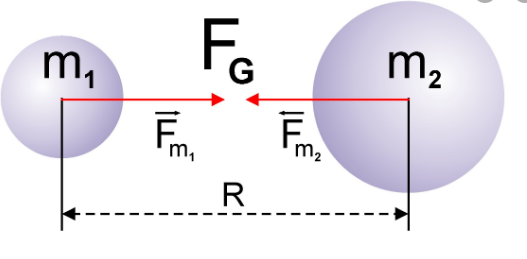
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1 = 1 кг и m2 = 1 кг, то F = G.
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.
Расчет силы тяжести на Земле
Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.
Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:
Формула расчета ускорения свободного падения
Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙10 22 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
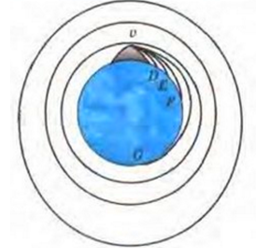
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.
Определение Первая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Вывод формулы первой космической скорости
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:
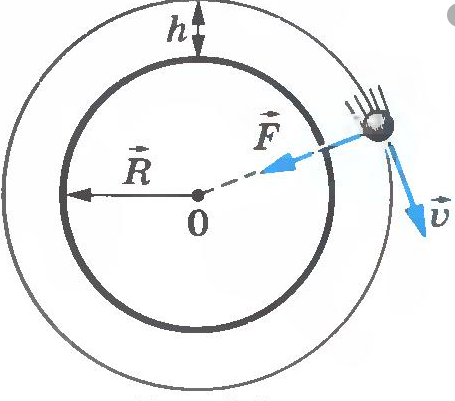
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:
Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙10 24 кг, а ее радиус равен 6052 км.
Алгоритм решения
Решение
Запишем исходные данные:
Запишем закон всемирного тяготения:
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 3 2 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?
Какая величина является мерой гравитационного взаимодействия тел
Все тела обладающие массой притягиваются друг к другу. Исаак Ньютон на основе многолетних данных астрономических наблюдений и законов динамики сформулировал закон всемирного тяготения : две любые материальные точки массами m 1 и m 2 притягиваются друг к другу вдоль линии соединяющей точки с силой прямо пропорциональной произведению масс точек и обратно пропорциональной квадрату расстояния (r) между ними:
Земля не является «материальной точкой» для тел, расположенных на ее поверхности. Теоретически доказано, что сила, с которой Земля притягивает тела, расположенные вне ее, равна силе, которую создавала бы материальная точка массой (М), равной массе Земли, и расположенная в центре Земли. Назовем силой тяжести силу, с которой тело взаимодействует с планетой, вблизи которой оно находится.
В соответствии с законом всемирного тяготения на материальную точку массой (m) со стороны Земли будет действовать сила тяжести, равная
Если тело движется с ускорением равным ускорению силы тяжести, то вес тела будет равен нулю:
1) вес тела равен нулю когда тело движется с ускорением равным ускорению силы тяжести ( ) в лифте вертикально вниз;
Закон всемирного тяготения определяет величину и направление силы всемирного тяготения, но не отвечает на вопрос как осуществляется это взаимодействие. Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения, или гравитационного поля.
1. Напряженность гравитационного поля ( ), силовая характеристика поля, равна силе, действующей со стороны поля на материальную точку единичной массы, и совпадает по направлению с действующей силой (это ничто иное как ускорение, с которым тело движется в поле тяготения):
Независимо от своей массы все тела под действием силы тяжести движутся с одинаковым ускорением ( )
Единица измерения [φ]=Дж/кг.
Потенциальная энергия тела в гравитационном поле равна:
Тогда работа гравитационного поля по перемещению тела из точки с потенциалом φ 1 в точку с потенциалом φ 2 равна:
Работа гравитационного поля по перемещению тела между двумя точками не зависит от траектории движения тела, а определяется только разностью потенциалов начальной и конечной точек, на замкнутом пути работа гравитационного поля равна нулю. То есть, сила всемирного тяготения и сила тяжести являются консервативными.
В качестве примера рассмотрим гравитационное поле материальной точки.
Наглядную картину поля представляет набор линий напряженности и эквипотенциальных поверхностей, например, гравитационное поле материальной точки представлено на рисунке (1.8.2).
Мы уже упоминали, что гравитационное поле Земли можно рассматривать, как поле материальной точки расположенной в центре Земли. Тогда потенциальная энергия тела, находящегося на высоте h относительно Земли:
Потенциальная энергия тела на высоте h над поверхностью Земли, равна:
Рассмотрим взаимосвязь между потенциалом и напряженностью поля тяготения.
Элементарная работа, совершаемая полем при малом перемещении тела массой (m), равна
Величина dφ/dl характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения, это ничто иное, как градиент потенциала.
Таким образом, напряженность гравитационного поля численно равна градиенту потенциала гравитационного поля и направлена в сторону его уменьшения:
На Земле приблизительно инерциальными являются системы отсчета, которые покоятся или движутся равномерно и прямолинейно относительно точек на поверхности Земли.
Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, рассматривают три варианта проявления этих сил.
1. Сила инерции возникает при ускоренном поступательном движении системы отсчета и направлена против вектора ускорения неинерциальной системы отсчета :
Действию центробежной силы инерции подвергаются пассажиры в движущемся транспорте на поворотах; летчики при выполнении фигур высшего пилотажа; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах, где они достигают огромных значений. При проектировании быстро вращающихся деталей машин (роторов, винтов самолетов) принимаются специальные меры для уравновешивания центробежных сил инерции.
равна произведению удвоенной массы тела на векторное произведение скорости поступательного движения тела относительно системы отсчета и угловой скорости вращения системы отсчета. Эта сила направлена перпендикулярно векторам скорости тела и угловой скорости вращения системы в соответствии с правилом правого винта.
Земля представляет собой вращающуюся систему отсчета и действие силы Кориолиса объясняет ряд наблюдаемых на Земле явлений. Так, если тело движется в северном полушарии на север (рис.1.8.4), то сила Кориолиса будет направлена вправо по отношению к направлению движения, и тело отклонится на восток. Если тело движется в юг, то сила Кориолиса также направлена вправо по отношению к направлению движения, и тело отклонится на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые. Аналогично можно показать, что в южном полушарии сила Кориолиса, действующая на движущиеся тела, будет направлена влево по отношению к направлению движения.
Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета : произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции):
Обратим еще раз внимание на то, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета, поэтому они не подчиняются третьему закону Ньютона. Два основных положения механики: 1) ускорение всегда вызывается силой; 2) сила всегда обусловлена взаимодействием между телами, в неинерциальных системах отсчета одновременно не выполняются.
Таким образом, силы инерции действуют только в неинерциальных системах отсчета, в инерциальных системах отсчета таких сил не существует.
Все тела независимо от их масс и химического состава, получают в данном гравитационном поле одинаковые ускорения. Поэтому в таком поле они движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают свободно движущиеся тела, если их движение рассматривать относительно какой-либо неинерциальной системы отсчета.
Силы инерции, действующие на тела неинерциальной системе отсчета, пропорциональны их массам и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в «поле сил инерции» эти тела движутся совершенно одинаково, если только одинаковы начальные условия.
Все механические явления и движения в лифте будут в точности такими же, что и в неподвижном лифте, висящем в поле тяжести.
Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции.
Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сил и сил инерции.
Принципа эквивалентности Эйнштейна: все физические явления в поле сил тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы.
Принцип эквивалентности гравитационных сил и сил инерции можно рассматривать как принцип эквивалентности гравитационной и инерционной масс тела.
© ФГОУ ВПО Красноярский государственный аграрный университет, 2013
Гравитационное взаимодействие



Гравитационное взаимодействие – дальнодействующее. Это означает, что его радиус действия равен бесконечности.
Если поле тяготения достаточно слабое и тела движутся медленно, по сравнению со скоростью света, то справедлив закон всемирного тяготения Ньютона. Согласно этому закону, две материальные точки (под материальными точками в данном случае можно понимать любые тела, линейные размеры которых много меньше расстояния между ними) притягиваются с силой:
Важно отметить, что в законе всемирного тяготения масса выступает в качестве меры гравитации, т.е. определяет силу тяготения между материальными телами.
Важность закона всемирного тяготения состоит в том, что Ньютон, таким образом, динамически обосновал систему Коперника и законы Кеплера.
В третьей части книги Ньютон изложил Общую Систему Мира и небесную механику, в частности, теорию сжатия Земли у полюсов, теорию приливов и отливов, движения комет, возмущения в движении планет и т.д. на основе закона всемирного тяготения.
Утверждение Ньютона о том, что Земля сжата у полюсов, было экспериментально доказано в 1735-1744 гг. в результате измерения дуги земного меридиана в экваториальной зоне (Перу) и на севере (Лапландия) двумя экспедициями Парижской Академии наук.
Следующим большим успехом закона всемирного тяготения было предсказание ученым Клеро времени возвращения кометы Галлея. В 1682 г. Галлей открыл новую комету и предсказал ее возвращение в сферу земного наблюдения через 76 лет. Однако в 1758 г. комета не появилась, и Клеро сделал новый расчет времени ее появления на основе закона всемирного тяготения с учетом влияния Юпитера и Сатурна. Назвав время ее появления – 4 апреля 1759 г., Клеро ошибся всего на 19 дней.
(Успехи теории тяготения в решении проблем небесной механики продолжались и в 19 веке. Так в 1846 г. французский астроном Леверье писал своему немецкому коллеге Галле: «направьте ваш телескоп на точку эклиптики в созвездии Водолея на долготе 326 градусов, и вы найдете в пределах одного градуса от этого места новую планету с заметным диском, имеющую вид звезды приблизительно девятой величины.» Эта точка была вычислена Леверье и независимо от него Адамсом (Англия) на основе закона всемирного тяготения при анализе наблюдаемых «неправильностей» в движении Урана и предположения, что вызываются они влиянием неизвестной планеты. И действительно, 23 сентября 1846 г. Галле в указанной точке неба обнаружил новую планету. Так родились слова «Планета Нептун открыта на кончике пера».)
В общем случае, который включает сильные поля тяготения и высокие скорости движения, сравнимые со скоростью света, тяготение описывается общей теорией относительности (ОТО). ОТО является обобщением ньютоновской теории тяготения на основе специальной теория относительности (СТО).
Теория Эйнштейна описывает тяготение как воздействие физической материи на свойства четырехмерного пространства-времени. Оно, в свою очередь, влияет на движение материи и другие физические процессы. Так, ОТО установлено, что материя искривляет пространство-время. И это искривление, проявляемое как тяготение, влияет на движение материи. В таком пространстве-времени движение тел по инерции, т.е. при отсутствии внешних сил, происходит уже не по прямым, а по искривленным линиям (геодезическим линиям) и с переменной скоростью. Геометрия обычного трехмерного пространства оказывается неэвклидовой (она описывается геометрией Римана).
Эйнштейновская теория тяготения приводит, по сравнению с ньютоновской, к качественно новым эффектам:
а) к существованию гравитационных волн, испускаемых неравномерно движущимися телами;
б) к гравитационному изменению длины волны света в сильном поле тяготения;
Он определяется массой М и равен
где g = 6,7·10-8см3г-1сек-2-гравитационная постоянная;
По современным представлениям, “черная дыра” может образоваться в конце эволюция массивной сверхновой звезды.
Необходимо отметить, что многие представления ОТО с хорошей точностью подтверждаются экспериментально.
Гравитационное поле должно подчиняться квантовым законам, как и все остальные физические поля. Квантовая теория гравитации не завершена. Но в ней гравитационные волны рассматриваются как поток квантов – гравитонов. Гравитоны представляют собой электрически нейтральные частицы с нулевой массой покоя. В подавляющем большинстве мыслимых процессов во Веленной квантовые эффекты гравитация чрезвычайно слабы. Но вблизи особых точек, где искривление пространства-времени очень велико, квантовые эффекты должны быть существенными. ОТО предсказывает, что квантовые эффекты гравитации должны быть определяющими, когда радиус кривизны пространства-времени становится равным величине
Расстояниеrпл- называют планковской длиной. В таких условиях ОТО неприменима.
Считается, что трудности в построении теории элементарных частиц могут быть устранены с учетом гравитационного взаимодействия на очень малых расстояниях – порядка 10-33 см. На таких расстояниях будет сказываться изменение геометрии пространства-времени за счет гравитации. Есть предположение, что планковская длина – это гипотетическая универсальная постоянная размерности длины, определяющая пределы применимости фундаментальных физических представлений теории относительности, квантовой теории, принципа причинности.
Закон всемирного тяготения
Гравитационное взаимодействие
Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.
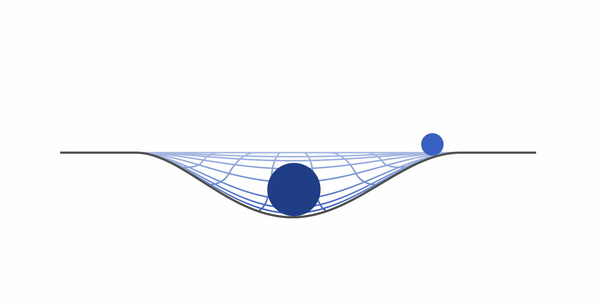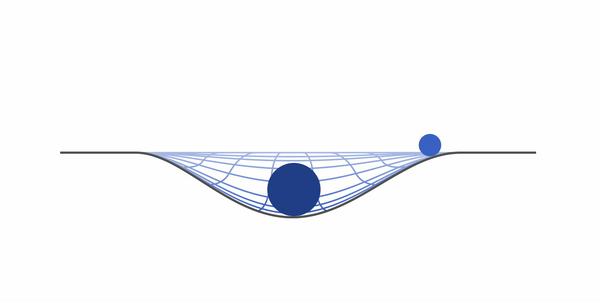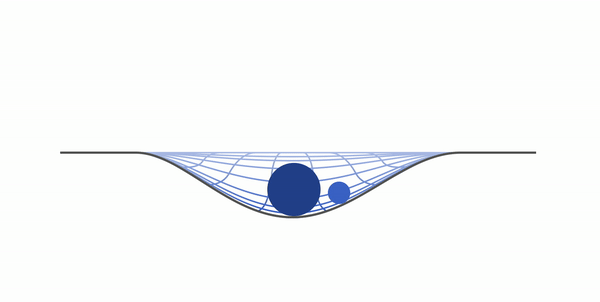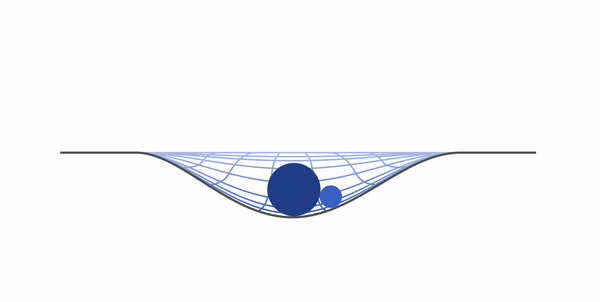
Возьмем два тела — одно с большой массой, другое с маленькой. Натянем гигантское полотно ткани и положим на него тело с большей массой. После чего положим туда тело с массой поменьше. Мы будем наблюдать примерно такую картину:
Маленькое тело начнет притягиваться к тому, что больше, — это и есть гравитация. По сути, Земля — это большой шарик, а все остальные предметы — маленький (даже если это вовсе не шарики).
Гравитационное взаимодействие универсально. Оно справедливо для всех видов материи. Гравитация проявляется только в притяжении — отталкивание тел гравитация не предусматривает.
Из всех фундаментальных взаимодействий гравитационное — самое слабое. Хотя гравитация действует между всеми элементарными частицами, она настолько слаба, что ее принято не учитывать. Все дело в том, что гравитационное взаимодействие зависит от массы объекта, а у частиц она крайне мала. Эту зависимость впервые сформулировал Исаак Ньютон.
Закон всемирного тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения
F — сила тяготения [Н]
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей.
Задачка раз
Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планеты к звезде?
Решение
По закону всемирного тяготения сила притяжения планеты к звезде обратно пропорциональна квадрату радиуса орбиты. Таким образом, в силу равенства масс отношение сил притяжения к звезде первой и второй планет обратно пропорционально отношению квадратов радиусов орбит:
По условию, у первой планеты радиус орбиты вдвое больше, чем у второй, то есть R1=2R2.
Ответ: отношение сил притяжения первой и второй планет к звезде равно 0,25.
Задачка два
У поверхности Луны на космонавта действует сила тяготения 144 Н. Какая сила тяготения действует со стороны Луны на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Луны на расстоянии трех лунных радиусов от ее центра?
Решение
По закону всемирного тяготения сила притяжения космонавта со стороны Луны обратно пропорциональна квадрату расстояния между ним и центром Луны. У поверхности Луны это расстояние совпадает с радиусом спутника. На космическом корабле, по условию, оно в три раза больше. Таким образом, сила тяготения со стороны Луны, действующая на космонавта на космическом корабле, в 9 раз меньше, чем у поверхности Луны, то есть:
Ответ: на расстоянии трех лунных радиусов от центра сила притяжения космонавта будет равна 16 Н.
Правильно говорить не «на тело действует сила тяготения», а «Земля притягивает тело с силой тяготения».
Ускорение свободного падения
Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.
Сила тяжести — сила, с которой Земля притягивает все тела.
Сила тяжести
F — сила тяжести [Н]
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
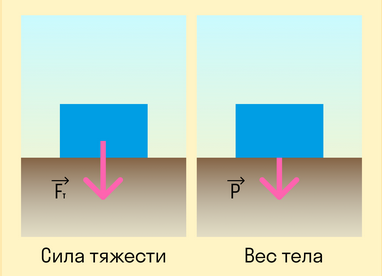
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.
Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
Приравниваем правые части:
Делим на массу левую и правую части:
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.
Закон всемирного тяготения
g — ускорение свободного падения [м/с 2 ]
M — масса планеты [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.
Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.
Но разве это не зависит еще и от массы предмета?
Нет, не зависит. На самом деле все тела падают одинаково вне зависимости от массы. Если мы возьмем перо и мяч, то перо, конечно, будет падать медленнее, но не из-за ускорения свободного падения. Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.
Третий закон Ньютона
Третий закон Ньютона обобщает огромное количество опытов, которые показывают, что силы — результат взаимодействия тел.
Он звучит так: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.
Если попроще — сила действия равна силе противодействия.
Если вам вдруг придется объяснять физику во дворе, то можно сказать и так: на каждую силу найдется другая сила. 🙈
Третий закон Ньютона
F1 — сила, с которой первое тело действует на второе [Н]
F2 — сила, с которой второе тело действует на первое [Н]
Так вот, для силы тяготения третий закон Ньютона тоже справедлив. С какой силой Земля притягивает тело, с той же силой тело притягивает Землю.
Задачка для практики
Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю?
Решение
Согласно третьему закону Ньютона, сила, с которой Земля притягивает мяч, равна силе, с которой мяч притягивает Землю.
Ответ: мяч притягивает Землю с силой 5 Н.
Поначалу это кажется странным, потому что мы ассоциируем силу с перемещением: мол, если сила такая же, то на то же расстояние подвинется Земля. Формально это так, но у мяча масса намного меньше, чем у Земли. И Земля смещается на такое крошечное расстояние, притягиваясь к мячу, что мы его не видим, в отличие от падения мяча.
Если каждый брошенный мяч смещает Землю на какое-то расстояние, пусть даже крошечное, возникает вопрос — как она еще не слетела с орбиты из-за всех этих смещений. Но тут как в перетягивании каната: если его будут тянуть две равные по силе команды, канат никуда не сдвинется. Так же и с нашей планетой.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)