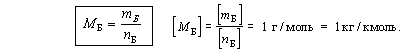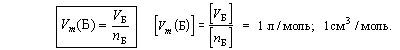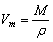какая величина характеризует род материала
Исходные понятия



Свойство – сторона предмета, обуславливающая его различие или сходство с другими предметами и проявляющаяся во взаимодействии с ними[5].
Например, о красном предмете говорится, что он обладает свойством «красноты».
В ГОСТ 15467-79 свойство трактуется как объективная особенность продукции, которая может проявляться при ее создании, эксплуатации или потреблении[6].
Свойства, для которых невозможно определить величину, обычно называют качественными свойствами (нет количества).
Например, величины: диаметр, длина окружности и длина волны — как правило, рассматриваются как однородные величины, а именно как относящиеся к роду величин, называемых длиной.
Как мы увидим далее, для величин одного рода определена, как правило, одна единица измерения. В данном примере это метр.
В последнее время все большее распространение получает подразделение величин на физические и нефизические, хотя следует отметить, что пока нет строгого критерия для такого деления величин [7].
При этом [7] под физическимипонимают величины, которые характеризуют свойства физического мира и применяются в физических науках и технике. Для них существуют единицы измерения. Физические величины в зависимости от правил их измерения подразделяются на три группы:
— величины, характеризующие свойства объектов (длина, масса);
— величины, характеризующие состояние системы (давление, температура);
— величины, характеризующие процессы (скорость, мощность).
«К нефизическимотносят величины, для которых нет единиц измерения. Они могут характеризовать как свойства материального мира, так и понятия, используемые в общественных науках, экономике, медицине. В соответствии с таким разделением величин принято выделять измерения физических величин и нефизические измерения.
Другим выражением такого подхода являются два разных понимания понятия измерения:
— измерение в узком смысле как экспериментальное сравнение одной измеряемой величины с другой известной величиной того же качества, принятой в качестве единицы;
— измерение в широком смысле как нахождение соответствий между числами и объектами, их состояниями или процессами по известным правилам.
Второе определение появилось в связи с широким распространением в последнее время измерений нефизических величин, которые фигурируют в медико-биологических исследованиях, в частности, в психологии, в экономике, в социологии и других общественных науках. В этом случае правильнее было бы говорить не об измерении, а об оценивании величин, понимая оценивание как установление качества, степени, уровня чего-либо в соответствии с установленными правилами. Другими словами, это операция по приписыванию путем вычисления, нахождения или определения числа величине, характеризующей качество какого-либо объекта, по установленным правилам. Например, определение силы ветра или землетрясения, выставление оценки фигуристам или оценок знаний учащихся по пятибалльной шкале»[7].
Другими словами единица измерения это величина данного рода, численное значение которой равно 1.
Далее мы будем рассматривать, так называемое, основное уравнение метрологии:
Предположим, в частности, что Х это, например, длина 50 метрового коридора. Тогда [Х] это единица измерения длины – метр, а q в данном случае равно 50.
Таким образом величины рода длина могут быть самыми разными, а единица измерения длины в принятой системе единиц одна – метр.
Мокров Ю. Метрология, стандартизация, сертификация
ОГЛАВЛЕНИЕ
Часть 1. МЕТРОЛОГИЯ
Глава 1. Метрология как наука об измерениях
1.1. Понятие и основные проблемы метрологии
Метрология состоит из следующих основных разделов:
Выделение законодательной метрологии с самостоятельный раздел обусловлено необходимостью законодательного регулиро-вания и контроля со стороны государства за деятельностью по обеспечению единства измерений.
Деятельность по обеспечению единства измерений (ОЕИ) регулируется Законом РФ «Об обеспечении единства измерений», принятом в 1993 г. Это закон устанавливает правовые основы обеспечения единства измерений в РФ. Он регулирует отношения государственных органов управления РФ с физическими и юридическими лицами по вопросам изготовления, выпуска, эксплуатации, ремонта, продажи, поверки и импорта средств измерений и направлен на защиту интересов граждан и экономики страны от отрицательных последствий недостоверных результатов измерений. Подробнее правовые вопросы обеспечения единства измерений рассматриваются ниже в соответствующем разделе.
В России сформирована Государственная система обеспе-чения единства измерений (ГСИ) как система управления деятельностью по обеспечению единства измерений, возглавляемая, реализуемая и контролируемая Федеральным агентством по техническому регулированию и метрологии (Ростехрегулиро-ванием). Целью ГСИ является создание общегосударственных правовых, нормативных, организационных, технических условия для решения задач по ОЕИ Нормативная база ГСИ насчитывает более 2500 обязательных и рекомендательных документов, регламентирующих практически все аспекты в области метрологии. Подробнее о задачах и составе ГСИ будет сказано в разделе о правовых основах ОЕИ.
В настоящей главе рассматриваются основные понятия, входящие в определение метрологии.
Измерение является одной из самых древнейших операций в процессе познания человеком окружающего материального мира. Вся история цивилизации представляет собой непрерывный процесс становления и развития измерений, совершенствования средств методов и измерений, повышения их точности и единообразия мер.
В процессе своего развития человечество прошло путь от измерений на основе органов чувств и частей человеческого тела до научных основ измерений и использования для этих целей сложнейших физических процессов и технических устройств. В настоящее время измерениями охватываются все физические свойства материи практически независимо от диапазона изменения этих свойств.
С развитием человечества измерения приобретали все большее значение в экономике, науке, технике, в производственной деятельности. Многие науки стали называться точными благодаря тому, что они могут устанавливать с помощью измерений количественные соотношения между явлениями природы. По существу, весь прогресс науки и техники неразрывно связан с возрастанием роли и совершенствованием искусства измерений. Д.И. Менделеев говорил, что «наука начинается с тех пор, как начинают измерять. Точная наука немыслима без меры».
Не меньшее значение имеют измерения в технике, производственной деятельности, при учете материальных ценностей, при обеспечении безопасных условий труда и здоровья человека, в сохранении окружающей среды. Современный научно-технический прогресс невозможен без широкого использования средств измерений и проведения многочисленных измерений.
В нашей стране проводится более десятки миллиардов измерений в день, свыше 4 млн. человек считают измерение своей профессией. Доля затрат на измерения составляет (10-15) % всех затрат общественного труда, достигая в электронике и точном машиностроении (50-70) %. В стране используется около миллиарда средств измерений. При создании современных электронных систем (ЭВМ, интегральных схем и т. п.) до (60-80) % затрат приходится на измерения параметров материалов, компонентов и готовых изделий.
Все это говорит о том, что невозможно переоценить роль измерений в жизни современного общества.
Хотя человек проводит измерения с незапамятных времен и интуитивно этот термин представляется понятным, точно и правильно определить его не просто. Об этом говорит, например, дискуссия по вопросам понятия и определения измерения, прошедшая не так давно на страницах журнала «Измерительная техника». В качестве примера ниже приводятся различные определения понятия «измерение», взятые из литературы и нормативных документов разных лет.
Из рассмотрения приведенных определений понятия «измерение» наиболее предпочтительным, включающим в себя в той или иной мере все другие приведенные определения, следует считать определение, приведенное в РМГ 29-99. В нем учтена техническая сторона измерения как совокупность операций по применению технического средства, показана метрологическая суть измерения как процесса сравнения с размером единицы (мерой) и представлена познавательная сторона измерения как процесса получения значения величины.
Приведенные выше определения измерения могут быть выражены уравнением, которое в метрологии называется основным уравнением измерений:

где 


Во всех определениях измерения присутствует понятие величины, или более строго, физической величины.
1.3 Физические величины и их измерения
— величины, характеризующие процессы (скорость, мощность).
К нефизическим относят величины, для которых нет единиц измерения. Они могут характеризовать как свойства материального мира, так и понятия, используемые в общественных науках, экономике, медицине. В соответствии с таким разделением величин принято выделять измерения физических величин и нефизические измерения. Другим выражением такого подхода являются два разных понимания понятия измерения:
одной измеряемой величины с другой известной величиной того
же качества, принятой в качестве единицы;
между числами и объектами, их состояниями или процессами по
известным правилам.
Второе определение появилось в связи с широким распространением в последнее время измерений нефизических величин, которые фигурируют в медико-биологических исследованиях, в частности, в психологии, в экономике, в социологии и других общественных науках. В этом случае правильнее было бы говорить не об измерении, а об оценивании величин, понимая оценивание как установление качества, степени, уровня чего-либо в соответствии с установленными правилами. Другими словами, это операция по приписыванию путем вычисления, нахождения или определения числа величине, характеризующей качество какого-либо объекта, по установленным правилам. Например, определение силы ветра или землетрясения, выставление оценки фигуристам или оценок знаний учащихся по пятибалльной шкале.
Понятие оценивание величин не следует путать с понятием оценки величин, связанным с тем, что в результате измерений мы фактически получаем не истинное значение измеряемой величины, а лишь его оценку, в той или иной степени близкую к этому значению.
Рассмотренное выше понятие «измерение», предполагающее наличие единицы измерения (меры), соответствует понятию измерения в узком смысле и является более традиционным и классическим. В этом смысле оно и будет пониматься ниже — как измерение физических величин.
Ниже приведены основные понятия, относящиеся к физической величине (здесь и далее все основные понятия по метрологии и их определения приводятся по упомянутой выше рекомендации по межгосударственной стандартизации РМГ 29-99):
— размер физической величины — количественная определенность физической величины, присущая конкретному материальному объекту, системе, явлению или процессу;
— значение физической величины — выражение размера физической величины в виде некоторого числа принятых для нее единиц;
— истинное значение физической величины — значение физической величины, которое идеальным образом характеризует в качественном и количественном отношении соответствующую физическую величину (может быть соотнесено с понятием абсолютной истины и получено только в результате бесконечного процесса измерений с бесконечным совершенствованием методов и средств измерений);
1.4 Шкалы измерений
1.5 Системы физических величин
Для того чтобы можно было провести измерение и достичь поставленную перед ним цель, необходимо сформулировать измерительную задачу, в которую должны войти следующие составляющие элементы измерений:
1.7 Классификация измерений
В зависимости от рода измеряемой величины, условий проведения измерений и приемов обработки экспериментальных данных измерения могут классифицироваться с различных точек зрения.
С точки зрения общих приемов получения результатов они разделены на четыре класса:
1.8 Принципы, методы и методики измерений
Наряду с рассмотренными выше основными характеристиками измерений, в теории измерений рассматриваются такие их характеристики, как принцип и метод измерений.
Принцип измерений – физическое явление или эффект, положенное в основу измерения. Например, использование силы тяжести при измерении массы взвешиванием.
Метод измерений – прием или совокупность приемов сравнения измеряемой величины с ее единицей в соответствии с реализованным принципом измерений. Как правило, метод измерений обусловлен устройством средств измерений. Некоторыми примерами распространенных методов измерений являются следующие методы.
Метод непосредственной оценки – метод, при котором значение величины определяют непосредственно по показывающему средству измерений. Например, взвешивание на циферблатных весах или измерение давления пружинным манометром.
Дифференциальный метод – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами. Этот метод может дать очень точные результаты. Так, если разность составляет 0,1 % измеряемой величины и оценивается прибором с точностью до 1 %, то точность измерения искомой величины составит уже 0,001 %. Например, при сравнении одинаковых линейных мер, где разность между ними определяется окулярным микрометром, позволяющим ее оценить до десятых долей микрона.
Нулевой метод измерений – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля. Мера – средство измерений, предназначенное для воспроизведения и хранения физической величины. Например, измерение массы на равноплечных весах при помощи гирь. Принадлежит к числу очень точных методов.
Метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают величиной, воспроизводимой мерой. Например, измерение напряжения постоянного тока на компенсаторе сравнением с известной ЭДС нормального элемента. Результат измерения при этом методе либо вычисляют как сумму значения используемой для сравнения меры и показания измерительного прибора, либо принимают равным значению меры. Существуют различные модификации этого метода:
Понятие величины и ее измерения. Свойства скалярных величин. Действия над величинами. Натуральное число как результат измерения величины.
Ищем педагогов в команду «Инфоурок»
Понятие величины и ее измерения. Свойства скалярных величин. Действия над величинами. Натуральное число как результат измерения величины.
Длина отрезка как геометрическая величина, её измерение. Методика изучения длины и формирование навыков её измерения. Ознакомление с единицами длины и их соотношением.
При изучении раздела «Величины и их измерение» углубляются, систематизируются и обобщаются знания о величинах и их измерениях, известные из курса математики.
В теме «Понятие величины и её измерения» рассматривается несколько подходов к раскрытию содержания понятия скалярной величины. Из свойств скалярной величины обращаем внимание на те, которые явно или косвенно используются в курсе математики начальной школы. Дается понятие об измерении положительных скалярных величин как отображения некоторых объектов во множество положительных действительных чисел. Решая упражнения по теме, необходимо рассмотреть решение текстовых задач, сопровождая его анализом тех действий, которые выполнялись над величинами.
1. Понятие величины и ее измерения.
Величина – это размер. Существуют звёзды – карлики и гигантские водоросли, огромные белковые молекулы и ничтожные пылинки. Как всё это сопоставить друг с другом, что больше чего и во сколько раз?
Величина – одно из основных математических понятий, смысл которого с развитием математики подвергался ряду обобщений.
Начиная с дошкольного возраста, у детей формируются интуитивные представления о некоторых величинах и их измерении.
Учитель начальных классов должен не только продолжать эту работу на более высоком уровне, но и знакомить учащихся со свойствами, общими для всех величин.
Термин « величина» впервые появился в философской литературе и был связан с действительными числами.
Исторически числа возникли в процессе счёта предметов и измерения величин. Именно на это обстоятельство указывал Аристотель, когда писал: «То или иное количество есть множество, если его можно счесть; есть величина, если его можно измерить».
Мы знаем величины: дл, масса, емкость…
Тройки взаимосвязанных величин? (ск, вр, рас; цена, количество, стоимость)
Величина – неопределяемое понятие.
Под величиной понимают особые свойства реальных объектов или явлений.
«Величина» и «число» являются ведущими понятиями математики, физики, химии… поэтому формируются с 1 кл на примере длины.
Длина – это свойство предметов иметь протяжённость.
Масса – с математической точки зрения это такая положительная величина, которая обладает свойствами:
масса одинакова у тел, уравновешивающих друг друга на весах;
масса складывается, если тела соединяются вместе.
Длина и масса – разнородные величины, так как выражают разные свойства объектов.
Ещё различают величины (в геометрии векторная, скалярная; положительная, отрицательная; переменная, постоянная).
Например, при нагревании длина металлического стержня меняется (увеличивается).
Скалярные величины – величины, не имеющие направления или которые определяются одним численным значением.
В старших классах знания о величинах расширяются: изучают новые единицы ранее изученных величин, а также новые величины: сила, работа, мощность, сопротивление, ускорение, напряжённость…
Рассмотрим свойства однородных скалярных величин.
2. Свойства скалярных величин.
Любые две однородные величины сравнимы: они либо равны, либо одна меньше другой.
Т.е. для любых величин a и b справедливо одно и только одно из отношений:
Например, длина гипотенузы больше длины катета; масса яблока меньше массы арбуза, длины противоположных сторон прямоугольника равны.
2. Величины одного рода можно складывать, в результате сложения получается величина того же рода,
Т.е. для любых величин a и b однозначно определяется величина
Например: пусть а- длина отрезка АВ, в – длина отр. ВС. Тогда длина отрезка АС равна сумме длин отрезков АВ и ВС.
3. Действия над величинами.
В процессе решения практических задач у учащихся должно сложиться представление о величине как о свойстве предметов, которое позволяет их сравнивать, выполнять действия над ними.
Изучение величин связано с такими разделами курса, как «Нумерация» и «Арифметические действия». Методика изучения каждой величины имеет свои особенности, связанные со спецификой данной величины, но общий подход к величине как к свойству предметов и явлений позволяет говорить об общей методике изучения величин, которая включает следующие этапы:
I этап. Выявление представлений ребенка о данной величине. Введение понятия и соответствующего термина.
II этап. Сравнение однородных величин разными способами (визуально, ощущением, наложением, приложением, с помощью различных мерок).
III этап. Знакомство с единицей измерения величины и с измерительным прибором.
IV этап. Знакомство с новыми единицами измерения величин, с соотношениями между ними. Перевод мелких единиц измерения в более крупные и наоборот.
V этап. Сложение и вычитание однородных величин, выраженных в единицах различных наименований.
VI этап. Умножение и деление величины на число. Деление именованного числа на именованное.
Длина отрезка как геометрическая величина, её измерение.
Действия над отрезками, их свойства.
Понятие длины отрезка и ее измерения. Свойства числовых значений длины. Стандартные единицы длины, сведения об их происхождении.
Изучение темы «Длина отрезка и её измерение» дает теоретическое обоснование вопросов, связанных с изучением длины отрезка и ее измерения в начальной курсе математики. Здесь сравнивается процесс измерения длины отрезка на практике и в математике, рассматриваются основные свойства длин отрезков и история происхождения стандартных единиц длины.
Методика изучения длины и формирование навыков её измерения.
-Какую же мерку надо выбрать для измерения длин? Об этом надо договориться.
-Кто знает, как договорились люди? (Учащиеся могут назвать м, дм, см).
1) Величина – это то, что может быть измерено и результат измерения выражен числом. Длина является величиной.
2) Чтобы измерить величину, надо выбрать мерку и узнать, сколько раз она содержится в измеряемой величине.
3) Если изменяется мерка, то изменяется и значение величины. Поэтому сравнивать величины можно только тогда, когда они измерены одной и той же меркой.
4) Сейчас используются единые для всех стран единицы измерения длины. Одной из них является сантиметр.
Ознакомление с единицами длины и их соотношением.
В 
Какая величина характеризует род материала
5.1. Характеристики, свойства и физические величины
В предыдущих главах вы неоднократно сталкивались с характеристиками. Мы говорили о характеристиках химических веществ и реакций, о характеристиках атомов и атомных ядер, о характеристиках элементов и изотопов, а также других объектов или явлений.
Среди множества характеристик мы выделили характеристики, называемые свойствами объектов, выяснили, что свойства могут быть физическими и химическими, и познакомились с некоторыми из них.
Из курса физики вам известна еще одна группа характеристик. Это – физические величины. С ними мы сталкиваемся, как только хотим количественно описать какой-нибудь объект (или явление). Например, сравнивая атомы, мы говорим об их массе и о числе частиц, их составляющих. Сравнивая частицы, мы приводим их массу и электрический заряд. Описывая химическую реакцию, мы говорим о ее скорости, а характеризуя условия протекания реакции, используем физическую величину, называемую температурой. И так далее.
Таким образом, среди великого множества самых разнообразных характеристик объектов или явлений мы выделяем две большие группы: а) свойства – часть чисто качественных характеристик и б) физические величины – качественные и одновременно количественные характеристики этих объектов или явлений.
Следует четко различать сами объекты и явления (реально существуют или происходят в Природе), их характеристики и, в частности, свойства (проявляются объектами и явлениями) и физические величины (качественно и количественно характеризуют объекты или явления). Например: вещество свинец – объект, способность свинца плавиться – его свойство, а температура плавления свинца – физическая величина (в том числе говорящая нам, что свинец способен плавиться). Физические величины не являются свойствами, а свойства, в свою очередь, не могут быть физическими величинами. Перечисляя свойства и характеристики объекта, можно описать его только качественно, а, используя физические величины, можно охарактеризовать объект и качественно, и количественно.
Каждый объект (тело, вещество или частица), как правило, обладает несколькими свойствами и характеристиками и может характеризоваться несколькими разными физическими величинами.

а) ядро атома гелия-4,
б) атом углерода-12,
в) лёд.
Используйте известные вам физические величины для характеристики этих объектов.
2)Проиллюстрируйте ряд объект — свойство — физическая величина тремя примерами.
| Физическая величина (величина) – характеристика материального объекта (или явления), одинаковая в качественном отношении для многих объектов, но в количественном отношении индивидуальная для каждого объекта. |
В качественном отношении физическая величина показывает, что все объекты какой-либо группы обладают определенным свойством. В количественном отношении она показывает, насколько интенсивно конкретный объект проявляет это свойство.
| Род величины – качественная сторона этой величины, показывающая, какую особенность объекта данная величина характеризует. |
| Размер величины – количественная сторона этой величины, показывающая, насколько интенсивно данная особенность проявляется объектом. |
| Однородные величины – величины, одинаковые в качественном отношении (характеризующие одну и ту же особенность объектов). |
Следовательно, длина, ширина, высота, расстояние – однородные величины. Однородные величины можно сравнивать между собой по размеру. Так, мы можем сравнивать радиус атома с расстоянием между молекулами, массу атома с массой слитка металла, длительность урока с периодом обращения Земли вокруг Солнца. Но мы не можем сравнивать температуру воздуха в комнате с теплотой плавления льда или удельную теплоемкость меди с массой слитка этого металла – это пары величин разного рода (характеризуют разные свойства).
Размер величины для каждого объекта существует независимо от того, определяем мы его или нет. Очевидно, что и указка, и Останкинская башня имеют каждая вполне определенную длину, причем разную. Как же определить размер величины? Величину необходимо измерить, то есть сравнить с другой однородной величиной, служащей неким эталоном данной физической величины. В результате измерения мы получаем значение величины. Таким образом, значение физической величины возникает только в результате ее измерения.
Значение величины включает в себя числовое значение величины и единицу измерений.
| Числовое значение величины – отвлеченное число, входящее в значение величины. |
Числовое значение величины показывает, во сколько раз размер измеряемой величины больше размера единицы измерений. Следовательно, числовое значение величины зависит от размера выбранной единицы измерений.
| Единица измерений физической величины – физическая величина фиксированного размера, однородная измеряемой, которой условно присвоено числовое значение, равное единице. |
| Уравнения связи между величинами – уравнения, отражающие законы Природы, в которых под буквенными обозначениями понимаются величины. |
Изучение связей между величинами показало, что, если произвольно выбрать определенное число физических величин в качестве основных, то остальные величины (производные) могут быть выражены через основные величины с помощью уравнений связи. Все величины, вместе взятые, образуют систему физических величин.
| Основные физические величины – величины, входящие в систему величин и условно принятые независимыми от других величин системы. |
| Производные физические величины – величины, входящие в систему величин и определяемые через основные величины этой системы. |
| ИЮПАК – Международный союз теоретической и прикладной химии (IUPAC – International Union of Pure and Applied Chemistry) – неправительственная научная организация, входящая в Международный совет научных союзов. Создана в 1919 году для координации исследований в области химии и химической промышленности, требующих международного согласования, контроля и стандартизации. Членами ИЮПАК являются научные учреждения и промышленные фирмы более чем из 50 стран мира, и, кроме того, международные объединения по отдельным областям химии. В ведении ИЮПАК находится разработка общих принципов и правил химической номенклатуры, терминологии, символики; стандартизация методов измерений в области химии; создание баз данных по различным химическим направлениям, а также другие вопросы, требующие международных договоренностей. |

2.Как значения величины, выраженные в одних единицах измерений, выразить в других единицах? Приведите любые известные вам примеры.
С основными количественными характеристиками атомов вы познакомились в главе 4. Кроме числа протонов в ядре (Z), числа нейтронов в ядре (N) и массового числа (A) это
а) масса атома (нуклида), mо( A Э), [mо( A Э)] = 1 г или 1 кг;
б) атомная масса нуклида, Аr( A Э), [Аr( A Э)] =1 Дн;
в) средняя масса атомов элемента, 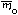
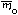
г) атомная масса элемента, Аr(Э), [Аr(Э)] = 1 Дн.
Проанализируем эти величины.
Так как масса атома и атомная масса нуклида – одна и та же величина, но измеренная разными единицами измерений, то
Совершенно аналогично, средняя масса атомов элемента и атомная масса элемента – также одна и та же величина, и в этом случае мы можем записать:
Химические вещества могут состоять из молекул (молекулярные вещества), а могут и не содержать таких обособленных незаряженных частиц (немолекулярные вещества).
Молекулы, как и атомы, естественно, обладают массой. Масса молекулы равна сумме масс составляющих ее атомов. Молекулы разных веществ имеют, как правило, разную массу. Молекулы одного вещества могут несколько отличаться друг от друга по массе, ведь в их состав могут входить атомы разных изотопов. Обычная вода, например, содержит молекулы 1 H2 16 O, 1 H 2 H 16 O, 2 H2 16 O, 1 H2 17 O, 1 H 2 H 17 O, 2 H2 17 O, 1 H2 18 O, 1 H 2 H 18 O и 2 H2 18 O.
В ядерной технике получают и используют вещества, состоящие из совершенно одинаковых молекул, например 2 H2 16 O или 1 H2 18 O, но с такими веществами, а их называют изотопно-чистыми, химики имеют дело крайне редко. Обычно чистое молекулярное вещество содержит молекулы, разные по изотопному составу и, соответственно, по массе.
Как посчитать среднюю массу молекулы такого обычного вещества, например H2O? Можно, конечно, посчитать массу молекулы каждого из изотопно-чистых веществ, экспериментально определить доли этих молекул в обычном веществе и, так же, как мы рассчитывали среднюю массу атома элемента в природной смеси изотопов, рассчитать среднюю массу молекулы. Но можно воспользоваться атомными массами элементов, ведь это уже средние массы, и в них учтены доли изотопов в природной смеси:
| Молекулярная масса вещества – средняя масса молекулы этого вещества, выраженная в дальтонах. |
Молекулярная масса вещества рассчитывается по молекулярной формуле.
Как и для атомов, для молекул (например, молекул воды) справедливы соотношения
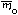
Для характеристики немолекулярных веществ (а иногда и молекулярных) используется формульная масса.
| Формульная масса вещества – средняя масса формульной единицы этого вещества, выраженная в дальтонах. |
Формульная масса рассчитывается по простейшей формуле, но обозначается так же, как и молекулярная масса – Mr, а масса формульной единицы – так же, как и масса молекулы – 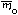
Для простого немолекулярного вещества формульная масса равна атомной массе элемента, например: Mr(К) = Аr(К), Мr(Fe) = Аr(Fe).
Для международной системы единиц (СИ) дальтон – внесистемная единица (то есть его в системе нет), поэтому, измеряя атомную, формульную или молекулярную массу, приходится массу соответствующей структурной единицы (то есть атома, молекулы или формульной единицы) сравнивать не с дальтоном (как единицей измерений), а с 1 /12 частью массы нуклида 12 С. Получающаяся величина (отношение) – величина безразмерная, она называется » относительная атомная (молекулярная, формульная) масса» и численно равна атомной (молекулярной, формульной) массе, выраженной в дальтонах. В химии использовать относительные массы очень неудобно!
Как отмерять взятые для реакции вещества, чтобы они прореагировали без остатка?
Очевидно, что отмерять вещества следует по числу атомов, молекул (для молекулярных веществ) или формульных единиц (для немолекулярных веществ). Обобщенно атомы, молекулы (реальные частицы), формульные единицы (выделенные нами » частицы» ) и другие составные части вещества называют структурными элементами. Число таких структурных элементов в порции вещества является физической величиной, называемой количество вещества. В нашем случае роль структурных элементов выполняют частицы – атомы алюминия и молекулы йода.
Количество вещества – физическая величина, равная числу структурных элементов, составляющих систему.
Значение постоянной Авогадро выбрано таким образом, чтобы числовое значение молярной массы любого вещества было равно числовому значению молекулярной массы, то есть
Числовое значение постоянной Авогадро <NA> называется числом Авогадро.
В Международной системе единиц определение моля формулируется несколько иначе.
| Моль – единица измерений количества вещества, равная количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в 12 граммах углерода-12. |
Но так как в 12 г углерода-12 содержится <NA> штук атомов углерода, оба эти определения не противоречат друг другу.
Применяются кратные и дольные единицы, производные от моля: 1 кмоль = 1000 моль, 1 ммоль = 0,001 моль и так далее.
Слово » моль» как обозначение единицы измерений не склоняется (5 моль; 0,25 моль), а в качестве названия единицы измерений (в тексте и устной речи) склоняется как существительное мужского рода (четверть моля, пятью молями, двух молей и тому подобное).
Число частиц в моле вещества (число Авогадро) очень велико, поэтому количество макрообъектов в молях обычно не измеряют, ведь даже звезд в Метагалактике всего лишь порядка одного моля.
Теперь запишем формально не строгое, но понятное определение количества вещества:
| Алюминий – Al – легкий пластичный металл. Как и все металлы – немолекулярное вещество. Алюминий сравнительно дешев и широко используется. Самая близкая любому человеку область его применения – многочисленные бытовые предметы: от кастрюль до фольги. Из измельченного до состояния пудры алюминия изготавливают » серебряную» краску. В некоторых странах, например в Венгрии, из алюминиевых сплавов делают монеты. Крупнейшими потребителями алюминия являются авиационная промышленность, машиностроение и строительство, не говоря уже о том, что большая часть электрических проводов (от линий электропередач до проводов в вашей квартире) делается из алюминия. Но так было не всегда. В течение некоторого времени после открытия (середина XIX века), алюминий был очень дорогим металлом, т. к. способы получения чистого алюминия были в то время слишком сложны. В те годы алюминиевые столовые приборы считались предметом роскоши. |
Из физики вам уже знакомы удельная теплоемкость, удельная теплота плавления, удельная теплота парообразования. Все это – удельные величины.
Удельная величина – отношение величины, характеризующей порцию вещества, к массе этой порции.
Удельная величина показывает значение соответствующей ей обычной величины для порции вещества массой 1 килограмм.
Но 1 кг меди содержит одно число атомов меди, а 1 кг свинца – совсем другое (где больше?). Очень часто, особенно при химических расчетах, использовать удельные величины бывает неудобно (почему?). В этом случае значение величины относят к стандартному числу частиц – к одному молю, то есть используют не удельные, а молярные величины.
Молярная величина – отношение величины, характеризующей порцию вещества, к количеству вещества этой порции.
Молярная величина показывает значение соответствующей обычной величины для 1 моля вещества.
С одной из молярных величин вы уже знакомы – это молярная масса.
Молярная масса вещества Б – отношение массы порции вещества Б к количеству вещества этой порции.
Молярная масса вещества соответствует массе 1 моля этого вещества.
Молярная масса вещества не зависит от внешних условий и агрегатного состояния вещества.
Молярная масса характеризует не только химические вещества, но и элементы, изотопы и любые другие совокупности более или менее одинаковых частиц (ионов, электронов и т. п.).
Другая часто используемая молярная величина – молярный объем.
| Молярный объем вещества Б – отношение объема порции вещества Б к количеству вещества этой порции. |
Молярный объем вещества соответствует объему 1 моля этого вещества.
Молярный объем зависит от температуры и давления и может быть определен для любого агрегатного состояния вещества.
К молярным величинам относится и постоянная Авогадро.
| Постоянная Авогадро (» молярное число частиц» ) – отношение числа частиц в порции вещества к количеству вещества этой порции. |
Три приведенные выше уравнения связи дают нам формулы для вычисления количества вещества, исходя из других данных:
В дальнейшем мы познакомимся и с другими молярными величинами.
В каких из этих веществ при кипении рвутся химические связи, а в каких межмолекулярные? Определите тип строения этих веществ.
7)Расположите молекулярные вещества, найденные вами в таблице (задача 6), в порядке возрастания прочности межмолекулярных связей.
8)Пользуясь данными той же таблицы, определите удельные теплоты кипения водорода, кислорода, воды, оксида бария и железа. Можно ли по полученным значениям сказать что-либо о типе структуры этих веществ?
9)Определите количество вещества хлорида натрия в образце этой соли массой 5,85 г.
10)Определите количества вещества в продажных (килограммовых) пачках поваренной соли и сахара (С12Н22О11). Почему эти количества вещества так сильно отличаются друг от друга?
11)Для проведения реакции необходимо взять 2,5 моля оксида кальция СаО. Сколько нужно отвесить этого вещества на весах?
12)Известно, что в результате реакции термического разложения гидроксида железа Fe(OH)2 образовалось 0,125 моль оксида железа FеО. Определите массу образовавшегося оксида железа.
13)В результате реакции было получено 6,4 г диоксида серы. Какова масса серы, содержащейся в этом диоксиде? Что в данном случае означает слово » сера» в вопросе задачи?
14)Оксид алюминия Al2O3 массой 306 г получили из алюминия массой 162 г. Докажите, что алюминий прореагировал полностью.
15)Из 268,8 г железа было получено 650 г трихлорида железа. Полностью ли прореагировало железо? Если нет, то какова масса непрореагировавшего железа?
16)В образце немолекулярного вещества массой 320 г содержится 4 моль этого вещества. Определите формульную массу вещества.
17)Установлено, что в образце желтого металла массой 1,97 г количество вещества составляет 0,01 моль. Какой это металл?
18)3,5 моля вещества с простейшей формулой СН2 имеют массу 196 г. Определите молекулярную формулу этого вещества.
19)Определите молекулярную формулу одной из аллотропных модификаций серы, если 0,02 моль этого вещества имеет массу 5,12 г.
20)При исследовании 6 г вещества с простейшей формулой HPO3 было установлено, что количество вещества в этой порции составляет 0,025 моль. Определите молекулярную формулу исследуемого вещества.
Уравнение связи Vm = V/n не дает нам возможности вычислить молярный объем конкретного вещества, так как непосредственное измерение количества вещества практически невозможно, а измерение объема особенно для твердых веществ часто бывает довольно сложным и трудоемким.
Преобразуем это уравнение. Вспомним, что
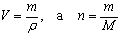
тогда 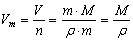
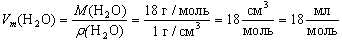
Аналогично определим молярные объемы некоторых других веществ и внесем их в таблицу:
Агрегатное состояние
Молярный объем,см 3 /моль
Примечание
твердое
твердая
твердый
жидкость
Мы с вами убедились, что для твердых и жидких веществ молярные объемы имеют разные значения, а для газов при одинаковых условиях эти значения очень близки. Совершенно одинаковы молярные объемы идеальных газов, то есть газов, в которых кроме упругих соударений между молекулами нет других видов взаимодействия. Подробнее идеальные газы вы будете изучать в курсе физики.
Под одинаковыми условиями понимается одинаковая температура и одинаковое давление. Мы с вами рассчитывали молярные объемы различных газов в условиях, обозначенных в примечании. Именно это сочетание давления и температуры получило название » нормальные условия» (сокращенное обозначение – н. у.).
При нормальных условиях
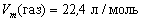 |
Для двух различных газов (1 и 2) количества вещества
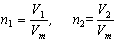
В равных объемах различных газов при одинаковых условиях содержится одинаковое число молекул.


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору