какая бывает симметрия в геометрии

Какая бывает симметрия в геометрии

Итак, что касается геометрии: выделяют три основных вида симметрии.

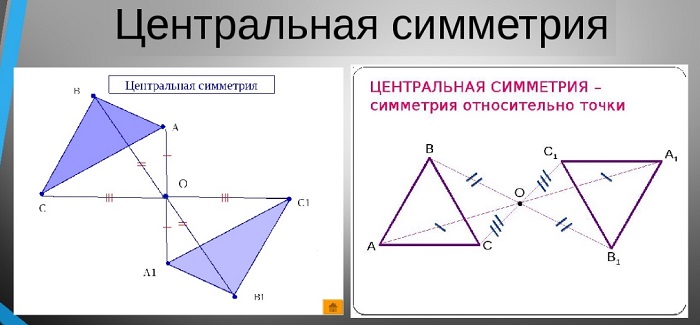
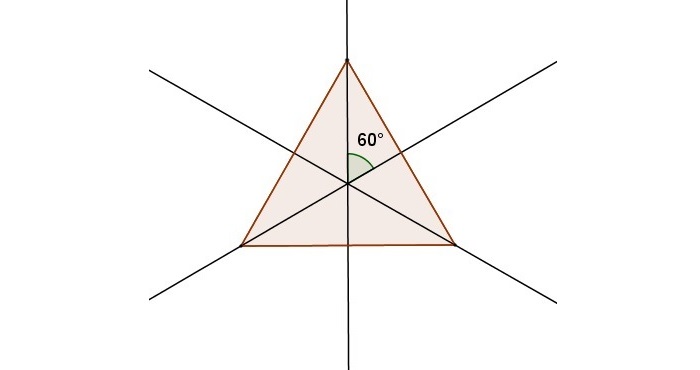
Во-первых, центральная симметрия (или симметрия относительно точки) – это преобразование плоскости (или пространства), при котором единственная точка (точка О – центр симметрии) остаётся на месте, остальные же точки меняют своё положение: вместо точки А получаем точку А1 такую, что точка О середина отрезка АА1. Чтобы построить фигуру Ф1, симметричную фигуре Ф относительно точки О, нужно через каждую точку фигуры Ф провести луч, проходящий через точку О (центр симметрии), и на этом луче отложить точку, симметричную выбранной относительно точки О. Множество построенных таким образом точек даст фигуру Ф1.

Большой интерес вызывают фигуры, имеющие центр симметрии: при симметрии относительно точки О любая точка фигурф Ф преобразуется опять же в некоторую точку фигуры Ф. Таких фигур в геометрии встречается много. Например: отрезок (середина отрезка – центр симметрии), прямая (любая её точка – центр её симметрии), окружность (центр окружности – центр симметрии), прямоугольник (точка пересечения его диагоналей – центр симметрии). Много центральносимметричных объектов в живой и неживой природе (сообщение учащихся). Часто люди сами создают объекты, имеющие центр симмет рии (примеры из рукоделия, примеры из машиностроения, примеры из архитектуры и много других примеров).

У прямоугольника их две, у квадрата – четыре, у круга – любая прямая, проходящая через его центр. Если присмотреться к буквам алфавита, то и среди них можно найти, имеющие горизонтальную или вертикальную, а иногда и обе оси симметрии. Объекты, имеющие оси симметрии достаточно часто встречаются в живой и неживой природе (доклады учащихся). В своей деятельности человек создаёт много объектов (например, орнаменты), имеющих несколько осей симметрии.

В-третьих, плоскостная (зеркальная) симметрия (или симметрия относительно плоскости) – это преобразование пространства, при котором только точки одной плоскости сохраняют своё местоположение (α-плоскость симметрии), остальные точки пространства меняют своё положение: вместо точки С получается такая точка С1, что плоскость α проходит через середину отрезка СС1, перпендикулярно к нему.

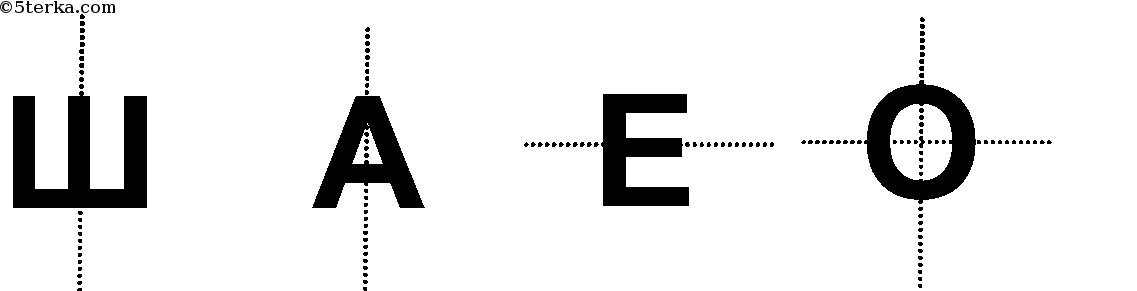
Чтобы построить фигуру Ф1,симметричную фигуре Ф относительно плоскости α, нужно для каждой точки фигуры Ф выстроить симметричные относительно α точки, они в своём множестве и образуют фигуру Ф1.

Источник

Осевая и центральная симметрия

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

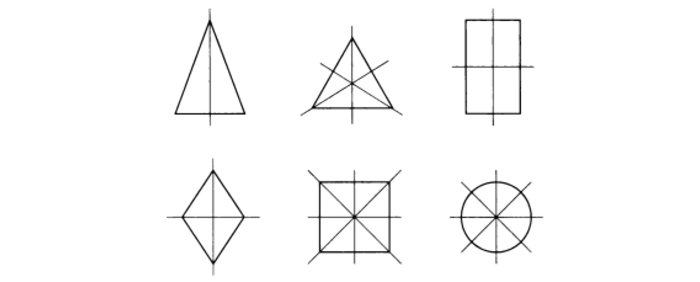
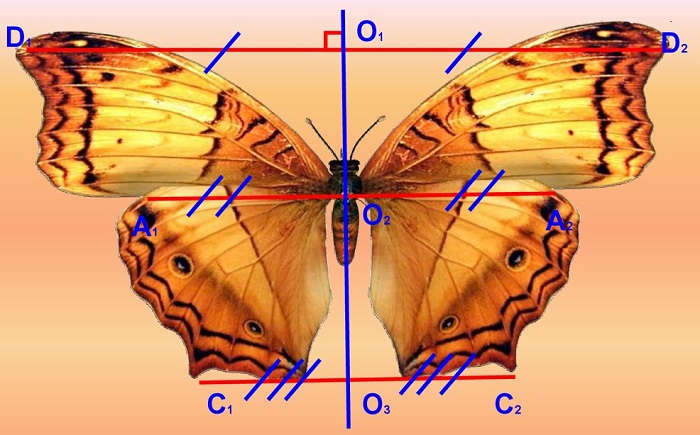
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

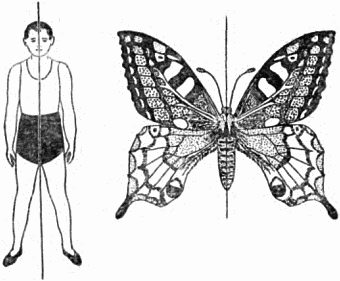
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

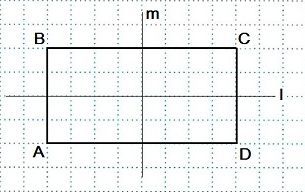
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

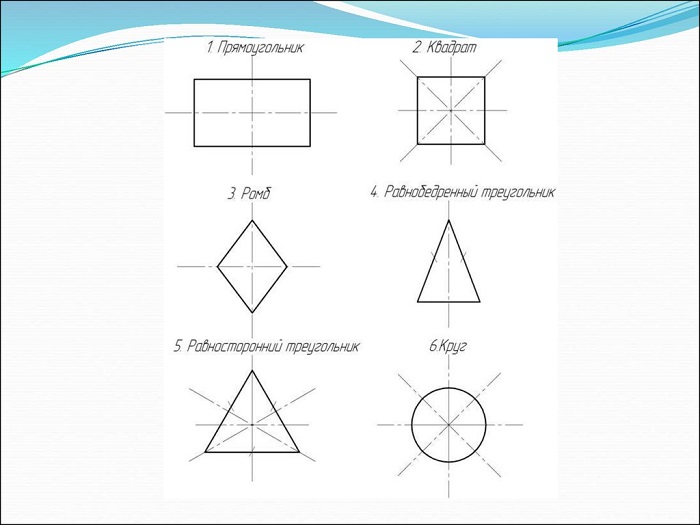
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

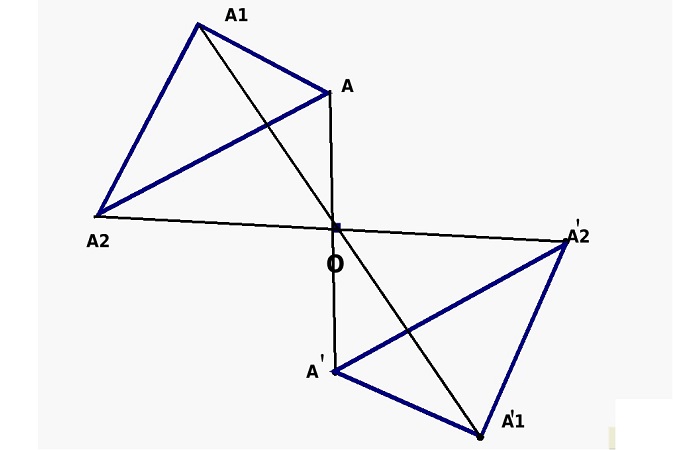
Пример 2. Постройте треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра (точки О).

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

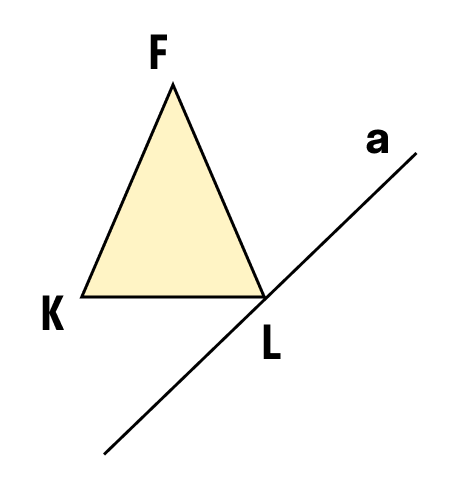
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Какая бывает симметрия в геометрии

Темы исследований

Оформление работы

Наш баннер

Исследовательские работы и проекты

Симметрия и виды симметрии

Симметрия и ее виды

Термин «симметрия» по-гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей». Математически строгое представление о симметрии сформировалось сравнительно недавно – в XIX веке. Современное определение симметрии выглядит примерно так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали.

1. Осевая симметрия.

Преобразование, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси l точку А, при этом отрезок АА l, называется осевой симметрией.

В частности, если при преобразовании симметрии относительно оси l фигура F переходит сама в себе, то она называется симметричной относительно оси l, а ось l называется ее осью симметрии.

2. Центральная симметрия

Преобразование, переводящее каждую точку А фигуры в точку А, симметричную ей относительно центра О, называется центральной симметрией

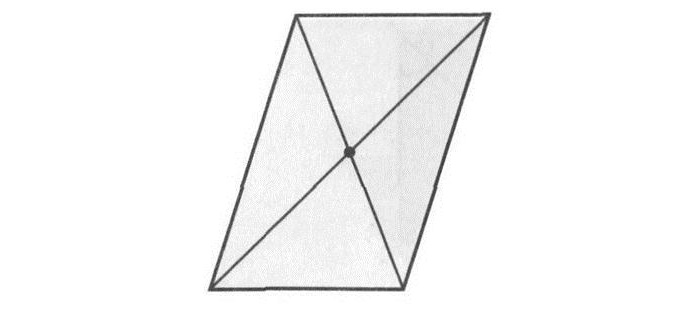
Точка О называется центром симметрии и является неподвижной. Если при преобразовании центральной симметрии относительно центра О фигура F преобразуется в себя, то она называется симметричной относительно центра О. Примерами таких фигур могут быть параллелограмм и окружность.

3. Поворот.

4. Параллельный перенос.

Преобразование при котором каждая точка фигуры (тела) перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.

5. Скользящая симметрия.

6. Зеркальная симметрия

Зеркальная симметрия является симметрией относительно отражения.

Зеркальную симметрию можно наблюдать на гербах городов.

Источник

Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.

Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.

Что такое симметрия

Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.

В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.

Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.

Рис. 1 Фигуры, обладающие симметричностью

Центральная симметрия

Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.

Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.

Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

Рис. 2 Графическое представление центральной симметрии

Осевая симметрия

Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.

Рис. 3 Наглядное представление осевой симметрии

В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.

Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.

Рис. 4 Примеры осевой симметрии

Фигуры, имеющие несколько осей симметрии

Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.

Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.

То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.

Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.

Рис. 5 Оси симметрии ромба

Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.

Рис. 6 Оси симметрии равностороннего треугольника

В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.

Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.

Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.

Источник

Методическая разработка «Урок геометрии в 8 классе «Виды симметрии»

Ищем педагогов в команду «Инфоурок»

2. Понятие симметрии и ее виды

3. Осевая симметрия

3.2. План построения

4. Центральная симметрия

4.2. План построения

5.1. Обобщающая таблица

5.2. Применение симметрии в различных областях

6. Домашнее задание

· Дать определение симметрии, познакомить с основными ее видами, научить строить симметричные фигуры относительно центра и оси.

· Дать представление о симметрии в русском языке, литературе, химии, физике, биологии.

· Показать возможности использования понятия «симметрия» при решении задач.

· Активизировать самостоятельную деятельность

· Развивать познавательную активность

· Учить обобщать и систематизировать полученную информацию

· Прививать культуру общения.

компьютер
мультимедийная приставка
видеоприставка
экран

2. Основные понятия симметрии и ее виды

Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека. И употреблялось скульпторами ещё в 5 веке до н. э. Слово “симметрия” греческое, оно означает “соразмерность, пропорциональность, одинаковость в расположении частей”. Его широко используют все без исключения направления современной науки. Об этой закономерности задумывались многие великие люди. Например, Л. Н. Толстой говорил: “Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано?”. Действительно симметричность приятна глазу. Кто не любовался симметричностью творений природы: листьями, цветами, птицами, животными; или творениями человека: зданиями, техникой, – всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии. Герман Вейль сказал: “Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”. Герман Вейль – это немецкий математик. Его деятельность приходится на первую половину ХХ века. Именно он сформулировал определение симметрии, установил по каким признакам усмотреть наличие или, наоборот, отсутствие симметрии в том или ином случае. Таким образом, математически строгое представление сформировалось сравнительно недавно – в начале ХХ века. Оно достаточно сложное. Мы же обратимся и еще раз вспомним те определения, которые даны нам в учебнике.

3. Осевая симметрия.

3.1 Основные определения

Определение. Две точки А и А₁ называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА₁ и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.

Определение. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.

3.2 План построения

И так, для построения симметричной фигуры относительно прямой от каждой точки проводим перпендикуляр к данной прямой и продлеваем его на такое же расстояние, отмечаем полученную точку. Так поступаем с каждой точкой, получаем симметричные вершины новой фигуры. Затем последовательно их соединяем и получаем симметричную фигуру данной относительной оси.

3.3 Примеры фигур, обладающих осевой симметрией.

Примем без доказательства, что при симметрии прямые переходят в прямые, причем сохраняются расстояния и углы.

4. Центральная симметрия

4.1 Основные определения

Определение. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

4.2 План построения

Построение треугольника симметричного данному относительно центра О.

Построение симметричных точек относительно центра.

На рисунке точки М и М₁, N и N₁ симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.

Вообще фигуры, симметричные относительно некоторой точ ки, равны.

Приведём примеры фигур, обладающие центральной симметрией. Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм.

Точка О называется центром симметрии фигуры. В подобных случаях фигура обладает центральной симметрией. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма- точка пересечения его диагоналей.

На рисунках показан угол симметричный относительно вершины, отрезок симметричный другому отрезку относительно центра А и четырехугольник симметричный относительно своей вершины М.

Примером фигуры, не имеющей центра симметрии, является треугольник.

Обобщим полученные знания. Сегодня на уроке мы познакомились с двумя основными видами симметрии: центральная и осевая. Посмотрим на экран и систематизируем полученные знания.

5.1 Обобщающая таблица

Все точки фигуры должны быть симметричны относительно какой-нибудь прямой.

Все точки фигуры должны симметричны относительно точки, выбранной в качестве центра симметрии.

1. 1. Симметричные точки лежат на перпендикулярах к прямой.

2. 2. Расстояние от точки до прямой равно расстоянию от прямой до симметричной точки.

3. 3. Прямые переходят в прямые, углы в равные углы.

4. 4. Сохраняются размеры и формы фигур.

5. 1. Симметричные точки лежат на прямой, проходящей через центр и данную точку фигуры.

6. 2. Расстояние от точки до прямой равно расстоянию от прямой до симметричной точки.

3. Сохраняются размеры и формы фигур.

5.2 Применение симметрии

С симметрией мы часто встречаемся на всех уроках и в окружающей жизни. Рассмотрим некоторые примеры.

На уроках алгебры мы изучили графики функций y = x и y = x

На рисунках представлены различные картинки, изображенные с помощью ветвей парабол.

(б) ромбический додекаэдр, (в) гексагональной октаэдр.

Печатные буквы русского алфавита тоже обладают различными видами симметрий.

А Д Л М П Т Ф Ш – вертикальная ось

Б Г И Й Р У Ц Ч Щ Я – ни какой оси

Радар шалаш Алла Анна

Могут быть палиндромическими и предложения.

Посмотрите на четверостишие А.С.Пушкина «Медный всадник». Если провести линию после второй строчки мы можем заметить элементы осевой симметрии

А роза упала на лапу Азора.

Я иду с мечем судия. ( Державин)

«Аргентина манит негра»,

«Ценит негра аргентинец»,

«Леша на полке клопа нашел».

В гранит оделася Не ва ;

Мосты повисли над вод ами;

Темно-зелеными сад ами

Ее покрылись остро ва …

рис1.

Обратите внимание на побеги листорасположения – это тоже своеобразный вид спирали – винтовая. Еще Гёте, который был не только великим поэтом, но и естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявлением самой сокровенной сущности жизни. Спирально закручиваются усики растений, по спирали происходит рост тканей в стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения (нутации) наблюдаются при росте корней и побегов. Очевидно, что в этом проявляется наследственность организации растений, а ее корни следует искать на клеточном и молекулярном уровнях.

Характерной чертой строения растений и их развития является спиральность.

Посмотрите на сосновую шишку. Чешуйки на ее поверхности расположены строго закономерно — по двум спиралям, которые пересекаются приблизительно под прямым углом. Число таких спиралей у сосновых шишек равно 8 и 13 или 13 и 21.

Различные виды симметрии физических явлений: симметрия электрического и магнитного полей (рис. 1)

Во взаимно перпендикулярных плоскостях симметрично распространение электромагнитных волн (рис. 2)

В произведениях искусства часто можно наблюдать зеркальную симметрию. Зеркальная» симметрия широко встречается в произведениях искусства примитивных цивилизаций и в древней живописи. Средневековые религиозные картины также характеризуются этим видом симметрии.

На современный вкус композиция такой картины скучна, поскольку симметрия слишком очевидна.

Молекула воды имеет плоскость симметрии (прямая вертикальная линия). : Исключительно важную роль в мире живой природы играют молекулы ДНК (дезоксирибонуклеиновая кислота) (рисунок 8). Это двуцепочечный высокомолекулярный полимер, мономером которого являются нуклеотиды. Молекулы ДНК имеют структуру двойной спирали, построенной по принципу комплементарности (рис. 9).

Издавна человек использовал симметрию в архитектуре. Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Причем древнегреческие архитекторы были убеждены, что в своих произведениях они руководствуются законами, которые управляют природой. Выбирая симметричные формы, художник тем самым выражал свое понимание природной гармонии как устойчивости и равновесия.

В городе Осло, столице Норвегии, есть выразительный ансамбль природы и художественных произведений. Это Фрогнер – парк – комплекс садово-парковой скульптуры, который создавался в течение 40 лет.

Дом Пашкова Лувр ( Париж)

Сегодня на уроках мы познакомились с понятием «симметрия», ее основными видами, научились строить симметричные фигуры, убедились, что симметрию можно обнаружить почти везде, если знать, как ее искать.

Многие народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».

6. Домашнее задание

Дается по вариантам задание домой на листочках, а также задание : провести свою исследовательскую работу по симметрии в области одного предмета.

3. Какие прямые при центральной симметрии переходят сами в себя?

4. Какая фигура симметрична окружности? Почему?

5. Нарисуйте фигуры симметричные фигурам, изображенным на рисунке 1.

7. Какие буквы русского алфавита имеют центр симметрии?

А, Б, В, Г, Д, Е, Ж, З, И, Й, К, Л, М, Н, О, П, Р, С, Т, У, Ф, Х, Ц, Ч, Ш, Щ, Ъ, Ы, Ь, Э, Ю, Я.

8. Какие буквы латинского алфавита имеют центр симметрии?

A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z.

3. Какие прямые при осевой симметрии переходят сами в себя?

4. Какая фигура симметрична окружности? Почему?

5. Нарисуйте фигуры симметричные фигурам, изображенным на рис. 1.

6. Восстановите фигуру, зная ее оси симметрии (рис. 2).

7. Какие буквы русского алфавита имеют оси симметрии?

А, Б, В, Г, Д, Е, Ж, З, И, Й, К, Л, М, Н, О, П, Р, С, Т, У, Ф, Х, Ц, Ч, Ш, Щ, Ъ, Ы, Ь, Э, Ю, Я.

8. Какие буквы латинского алфавита имеют оси симметрии?

A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z.

Защита исследовательских работ учащихся проведена на очередном уроке.

Источник