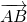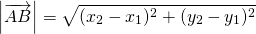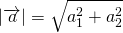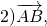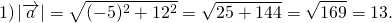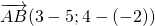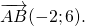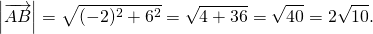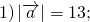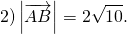кака найти длину вектора

Длина вектора

Длина вектора (или модуль вектора или абсолютная величина вектора) — это длина отрезка, изображающего вектор.

с началом в точке A(x₁; y₁) и концом в точке B(x₂; y₂) длину находим по формуле расстояния между точками:

Соответственно, для вектора

(то есть длина вектора равна квадратному корню из суммы квадратов его координат).

Найти длину вектора:

2) Если нужно найти длину вектора, зная координаты его начала и конца, удобнее сначала найти координаты вектора:

Теперь найдём его длину:

Длина (модуль) нулевого вектора равна нулю.

Источник

Урок о том, как найти длину вектора

Длина вектора

Формула длины вектора на плоскости: |overline| = sqrt

Формула длины вектора в пространстве: |overline| = sqrt

Если даны координаты точек начала и конца вектора A(a_x; a_y) и B(b_x; b_y), то найти длину можно по формулам:

Нахождение длины вектора: примеры и решения, формулы и теоремы

Длину вектора a→ будем обозначать a→. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора. Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат Oxy. Пусть в ней задан некоторый вектор a→ с координатами ax;ay. Введем формулу для нахождения длины (модуля) вектора a→ через координаты ax и ay.

Из теоремы Пифагора следует равенство OA2=OAx2+OAy2, откуда OA=OAx2+OAy2. Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что OAx2=ax2 и OAy2=ay2, а по построению длина OA равна длине вектора OA→, значит, OA→=OAx2+OAy2.

Отсюда получается, что формула для нахождения длины вектора a→=ax;ay имеет соответствующий вид: a→=ax2+ay2.

Если вектор a→ дан в виде разложения по координатным векторам a→=ax·i→+ay·j→, то вычислить его длину можно по той же формуле a→=ax2+ay2, в данном случае коэффициенты ax и ay выступают в роли координат вектора a→ в заданной системе координат.

Пример 1

Вычислить длину вектора a→=7;e, заданного в прямоугольной системе координат.

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатамa→=ax2+ay2: a→=72+e2=49+e

Формула для нахождения длины вектора a→=ax;ay;az по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

Отсюда следует, что длина вектора a→=ax;ay;az равна a→=ax2+ay2+az2.

Пример 2

Вычислить длину вектора a→=4·i→-3·j→+5·k→, где i→,j→,k→ — орты прямоугольной системы координат.

Дано разложение вектора a→=4·i→-3·j→+5·k→, его координаты равны a→=4,-3,5. Используя выше выведенную формулу получим a→=ax2+ay2+az2=42+(-3)2+52=52.

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A(ax;ay) и B(bx;by), отсюда вектор AB→ имеет координаты (bx-ax; by-ay)значит, его длина может быть определена по формуле: AB→=(bx-ax)2+(by-ay)2

А если даны точки с заданными координатами A(ax;ay;az) и B(bx;by;bz) в трехмерном пространстве, то длину вектора AB→ можно вычислить по формуле: AB→=(bx-ax)2+(by-ay)2+(bz-az)2

Пример 3

Найти длину вектора AB→, если в прямоугольной системе координат A1, 3, B-3, 1.

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим AB→=(bx-ax)2+(by-ay)2: AB→=(-3-1)2+(1-3)2=20-23. Второй вариант решения подразумевает под собой применение данных формул по очереди: AB→=(-3-1; 1-3)=(-4; 1-3); AB→=(-4)2+(1-3)2=20-23.-

Пример 4

Для начала распишем длину вектора AB→ по формуле: AB→=(bx-ax)2+(by-ay)2+(bz-az)2=(5-0)2+(2-1)2+(λ2-2)2=26+(λ2-2)2. Затем полученное выражение приравняем к 30, отсюда найдем искомые λ: 26+(λ2-2)2=3026+(λ2-2)2=30(λ2-2)2=4λ2-2=2 или λ2-2=-2 λ1=-2, λ2=2, λ3=0.

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов AB→, AC→ и угол между ними (или косинус угла), а требуется найти длину вектора BC→ или CB→. В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ABC, вычислить длину стороны BC, которая и равна искомой длине вектора. Рассмотрим такой случай на следующем примере.

Пример 5

Длины векторов AB→ и AC→ равны 3 и 7 соответственно, а угол между ними равен π3. Вычислить длину вектора BC→.

Длина вектора BC→ в данном случае равна длине стороны BC треугольника △ABC. Длины сторон AB и AC треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов:BC2=AB2+AC2-2·AB·AC·cos∠(AB,→AC→)=32+72-2·3·7·cosπ3=37 ⇒BC=37 Таким образом, BC→=37.

Итак, для нахождения длины вектора по координатам существуют следующие формулы a→=ax2+ay2 или a→=ax2+ay2+az2, по координатам точек начала и конца вектора AB→=(bx-ax)2+(by-ay)2 или AB→=(bx-ax)2+(by-ay)2+(bz-az)2, в некоторых случаях следует использовать теорему косинусов.

Источник

Характеристики вектора: длина, направление, координаты

У любого вектора есть 2 главные характеристики:

Третья характеристика вектора – это его координаты.

Примечание:

Зная координаты вектора, можно найти его длину и направление. Поэтому, задавать информацию о векторе можно двояко: либо указав его длину и направление, либо его координаты.

Что такое координаты вектора

Координаты вектора – это длины его теней на осях координат (его проекции на оси).

Координаты вектора указывают так:

\( a_ \) – это «x» координата вектора, проекция вектора \( \vec \) на ось Ox;

\( a_ \) — это «y» координата вектора, проекция вектора \( \vec \) на ось Oy;

Координаты вектора можно получить из координат его начальной и конечной точек:

«координата вектора» = «конец» — «начало»

Пример:

\( A \left( 1;1 \right) \) — начальная точка,

\( B \left( 4;3 \right) \) — конечная точка,

\[ \overrightarrow = \left\< AB_; AB_ \right\> \]

\[ \begin AB_ = 4 – 1; AB_ = 3 \\ AB_ = 3 – 1; AB_ = 2 \end \]

Длина вектора (в чем измеряется, как посчитать)

Длину вектора (его модуль) обозначают так:

Как вычислить длину вектора по его координатам

Когда известны координаты вектора, его длину считают так:

\( a_ \) и \( a_ \) — это числа, координаты вектора \( \vec \)

Для двухмерного вектора:

Для трехмерного вектора:

Как вычислить длину вектора с помощью рисунка

Если вектор нарисован на клетчатой бумаге, длину считаем так:

1). Если вектор лежит на линиях клеточек тетради:

— считаем количество клеточек.

Зная масштаб клеток, легко получить длину вектора – умножаем масштаб на количество клеток.

2). Если вектор не лежит вдоль линий:

— проводим вертикаль и горизонталь пунктиром.

\( \Delta x \) — горизонталь; \( \Delta y \) — вертикаль;

— затем применяем формулу:

Как указать направление вектора

Указать направление вектора можно с помощью его координат. Так как в его координатах уже содержится информация о длине и направлении вектора.

Бывает так, что координаты вектора неизвестны, а известна только лишь его длина. Тогда направление можно указать с помощью угла между вектором и какой-либо осью.

Для двумерного вектора

Если вектор двумерный, то для указания направления (см. рис. 10) можно использовать один из двух углов:

Словами указать направление вектора можно так:

Такой способ указания координат используют в полярной системе координат.

Для трехмерного вектора

Когда вектор располагается в трехмерном пространстве, чтобы указать, куда вектор направлен, используют два угла.

Такой способ указания координат используют в сферической системе координат.

Считаем Землю шаром. Расположим ее центр в начале трехмерной системы координат – точке (0 ; 0 ; 0).

Тогда координаты любой точки на поверхности планеты можно указать с помощью радиус-вектора этой точки.

Для указания сферических координат принято использовать:

Источник

Как найти длину вектора

Вы будете перенаправлены на Автор24

Понятие длины вектора

Для того, чтобы разобраться с понятием длины вектора, прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Введем теперь, непосредственно, понятие длин вектора.

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Готовые работы на аналогичную тему

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Теперь, найдя длину этого вектора по формуле, выведенной выше, мы и получим искомую длину. Получим:

Найдем для начала длины всех его сторон по формуле из замечания к задаче 2.

Источник

Модуль вектора. Длина вектора.

Определение длины вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Формулы длины вектора

Формула длины вектора для плоских задач

В случае плоской задачи модуль вектора a = < a_x ; a_y > можно найти воспользовавшись следующей формулой:

Формула длины вектора для пространственных задач

В случае пространственной задачи модуль вектора a = < a_x ; a_y ; a_z > можно найти воспользовавшись следующей формулой:

Примеры задач на вычисление длины вектора

Примеры вычисления длины вектора для плоских задачи

Решение: | a | = √ 3 2 + (-4) 2 = √ 9 + 16 = √ 25 = 5.

Примеры вычисления длины вектора для пространственных задачи

Решение: | a | = √ 2 2 + 4 2 + 4 2 = √ 4 + 16 + 16 = √ 36 = 6.

Примеры вычисления длины вектора для пространств с размерностью большей 3

Решение: | a | = √ 1 2 + (-3) 2 + 3 2 + (-1) 2 = √ 1 + 9 + 9 + 1 = √ 20 = 2√ 5

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник