как обозначается площадь в математике какой буквой
Площадь
Рассмотрим фигуру ниже:
Вся фигура состоит из 8 квадратов со стороной 1 см каждый.
Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.
В математике для нахождения площади геометрических фигур используют специальные формулы, в которых площадь обозначается заглавной латинской буквой « S ».
Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.
Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата, равна 1 м, то его площадь равна 1 квадратному метру ( 1 м 2 ); если длина его стороны равна 1 см, то его площадь равна 1 квадратному сантиметру ( 1 см 2 ).
Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.
Как перевести квадратные единицы
Рассмотрим квадрат со стороной 1 см.
S = 1 см · 1 см = 1см 2
Рассмотрим квадрат со стороной 1 м.
S = 1 м · 1 м = 1 м 2
Известно, что: 1 м = 100 см
1 м 2 = 1 м · 1 м = 100 см · 100 см = 10 000 см 2
Увеличим сторону квадрата равную 1 м в 10 раз. Получим квадрат со
стороной 10 м.
Площадь такого квадрата называют ар или сотка.
S = 10 м · 10 м = 100 м 2
В одном аре — сто квадратных метров.
Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».
1 ар (сотка) = 100 м 2
Значит: 1 ар (сотка) = 100 м 2 = 100 · 10 000 см 2 = 1 000 000 см 2
Увеличим сторону квадрата равную 10 м в 10 раз. Получим квадрат со
стороной 100 м.
Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование проговаривается полностью.
Выразим гектар в квадратных метрах.
1 га = 100 м · 100 м = 10 000 м 2
Теперь определим, сколько в одном гектаре аров.
Значит: 10 000 м 2 : 100 м 2 = 100 (ар)
1 км 2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м 2
Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.
Таблица переводов квадратных единиц
Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.
Как вычислить и обозначить площадь

Мерой протяжённости плоского участка Земли по длине и ширине является площадь. В математике она обычно обозначается латинской буквой S (от англ. «square» — «площадь», «квадрат») или греческой буквой σ (сигма). S обозначает площадь фигуры на плоскости или площадь поверхности тела, а σ — площадь поперечного сечения провода в физике. Это основные символы, хотя могут быть и другие, например, в сфере сопротивления материалов, А — площадь сечения профиля.
Формулы расчета
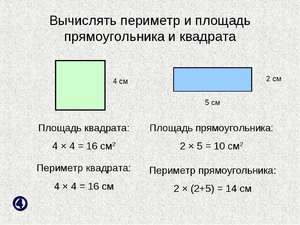
Чтобы найти площадь сложной плоской фигуры, её разбивают на множество простых фигур, таких как треугольники, трапеции или прямоугольники. Затем математическими методами выводят формулу для площади этой фигуры. Подобный метод используют не только в геометрии, но и в математическом анализе для вычисления площадей фигур, ограниченных кривыми.
Треугольник
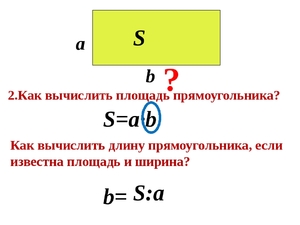
Четырёхугольник
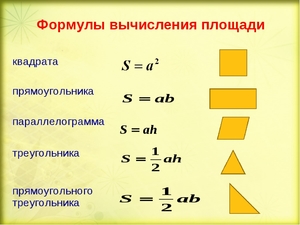
Затем по формулам вычислить их и сложить, т. е. S=S1+S2. Однако, если 4-угольник принадлежит к определённому классу, то его площадь можно найти по заранее известным формулам:
Многоугольник
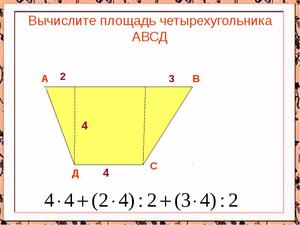
S=a•n•h/2=a²•n/[4•tg (180°/n)]=P²/[4•n•tg (180°/n)], где n — количество вершин (или сторон) многоугольника, a — сторона n-угольника, P — его периметр, h — апофема, т. е. отрезок, проведённый из центра многоугольника к одной из его сторон под углом 90°.
Найдём предел этого выражения при n→∞. Чтобы это сделать, учтём, что lim (cos (180°/n)) при n→∞ равен cos 0°=1 (lim — знак предела), а lim [1/(n•sin (180°/n))]= lim [1/(n•sin (π/n))] при n→∞ равен 1/π (мы перевели градусную меру в радианную, используя соотношение π рад=180°, и применили первый замечательный предел lim (sin x)/x=1 при x→∞). Подставив в последнее выражение для S полученные значения, придём к известной формуле:
Единицы измерения

В квадратных миллиметрах (мм²), например, измеряют площадь сечения проводов в электротехнике, в квадратных сантиметрах (см²) — сечения балки в строительной механике, в квадратных метрах (м²) — квартиры или дома, в квадратных километрах (км²) — территории в географии.
Однако иногда используются и внесистемные единицы измерения, такие, как: сотка, ар (а), гектар (га) и акр (ас). Приведём следующие соотношения:
Изучаем символы: как обозначается в математике площадь
В жизни каждого человека по достижении 7-летнего возраста появляется необходимость обучаться в средней общеобразовательной школе. В этом заведении ученик получает базовые знания и навыки. В рамках учебной программы по математике школьники узнают, как обозначается площадь. Необходимо рассмотреть, какой буквой и единицей измерения необходимо это делать.
Общие сведения

Под площадью понимается характеристика, имеющая числовое выражение. Ею описывается геометрическая фигура в двухмерном пространстве.
Объект, по отношению к которому возникает вопрос, как обозначить в письменном выражении площадь, может быть плоским или искривленным.Обозначение площади дает представление о размере и параметрах изучаемой площади.
В отдельных литературных источниках общая площадь встречается под названием квадратуры. Фигура, для которой возможно обозначить площадь, имеет наименование квадрируемой. Геометрические объекты, для которых значение площади в полученном решении оказалось одинаковым, встречаются под названием равновеликих.

Возможность практического измерения данной величины отмечается в результате использования планиметра и специальной палетки.
Важно! Основы геометрии: что это такое биссектриса треугольника
Площадь, обозначение которой становится доступным в результате ее числового выражения, характеризуется следующими параметрами:

Обратите внимание, к категории квадрируемой относится объект, поддающийся вписыванию в пределы многоугольника. Также достоверной является способность заключить многоугольник в данный квадрируемый объект.
Познавательно! Как найти и чему будет равна длина окружности
Общее понимание категории позволяет ее трактовать в качестве числовой характеристики. При этом этот признак используется по отношению только к поверхности двухмерной, находящейся в пространстве трехмерном.
Для данного показателя присуща система измерения. Основными единицами, дающими представление о величине геометрического объекта, являются сантиметры, миллиметры, дециметры, метры, километры. В ряде источников встречается упоминание проведенных измерений в арах, гектарах. Отличительная особенность, свойственная для рассматриваемого показателя, возведение единиц измерения в квадрат.
Важно! Урок геометрии: как найти по формуле периметр треугольника
Варианты обозначения

В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.
В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину.
В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение <эс>.
Обратите внимание! Знаком S обозначают площадь таких фигур, как квадрат, треугольник, ромб, прямоугольник, круг.

Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение. Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами. В качестве примера могут быть SAOB, SCLE, SOME.
Интересно! Что значит вертикально и как выглядит вертикальная линия
Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.
Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов. В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.
Полезное видео
Подведем итоги
Пространственное представление об изучаемом геометрическом объекте становится возможным благодаря площади. Обозначение данного показателя разнится в зависимости от выбранной дисциплины.
Геометрия
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Понятие площади многоугольника
Понятие площади уже знакомо нам из младших классов и повседневной жизни. Эта величина, которая, грубо говоря, характеризует размер плоских фигур. Она показывает, какую часть плоскости занимает та или иная фигура. Исторически понятие площади многоугольника считалось неопределяемым, так же как понятия точка, прямая, плоскость и т. д. Основная же задача геометров (а именно так называют математиков, специализирующихся на геометрии) сводилась к измерению площади.
Как известно, для проведения любых измерений должна существовать некоторая единица измерения. Так, массу измеряют в килограммах, длину – в метрах и т. д. При этом единицы измерения разных величин могут быть связаны друг с другом. С практической точки зрения удобно принять в качестве единицы измерения площади квадрат, сторона которого равна 1 метру. Принимается, что площадь такого квадрата равна 1 квадратному метру (обозначается символом м 2 ):
Аналогично можно определить такие величины, как квадратный сантиметр (см 2 ), квадратный километр (км 2 ), квадратный миллиметр (мм 2 ) и т.д.:
Как мы знаем, иногда в задачах единицу измерения длины не указывают вовсе. Например, говорят, что сторона квадрата равна единице. В таких случаях и площадь является безразмерной величиной. Принимается, что площадь квадрата со стороной, равной единице, также равна единице. Такой квадрат называется единичным.
Общепринято, что площадь фигуры обозначается буквой S.
Свойство аддитивности площади
Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:
Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.
В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:
Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.
Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.
Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.
Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:
В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:
Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:
Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.
Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут. Равносоставленные же фигуры могут и не накладываться друг на друга.
Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны. Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:
С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.
Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.
Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:
Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство
Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:
Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.
Площадь квадрата
Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.
Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:
Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:
В общем случае единичный квадрат можно разбить на m 2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:
Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.
Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:
Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:
В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине
Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».
Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:
Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R 2 ):
Задание. Найдите площадь квадрата, если его сторона равна
Задание. Площадь квадрата равна 25. Найдите длину его стороны.
Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:
Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:
Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.
Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:
По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:
Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.
Соотношение между единицами измерения площадей
Существуют специальные единицы измерения площади, известные как ар (обозначается сокращением а) и гектар (сокращение га). Первый представляет собой квадрат со стороной 10 м, а второй – со стороной 100 м. Верны следующие соотношения:
В частности, если стороны квадратов отличаются в 10 раз, то их площади отличаются уже в 100 раз. Отсюда вытекает быстрый метод перевода единиц площади. Пусть надо перевести 1 квадратный километр в квадратные дециметры. Сначала мы считаем, во сколько раз километр длиннее дециметра:
Решение. Миллиметр в 10 раз меньше сантиметра, а потому 1 см 2 равен 100 мм 2 :
Площадь прямоугольника
Ещё из младшей школы известно, что площадь прямоугольника равна произведению его сторон. Докажем этот факт, используя только свойства площади и выведенную нами ранее формулу площади квадрата.
Возьмем произвольный прямоугольник со сторонами a и b. Далее достроим его до квадрата со стороной (а + b):
Итак, мы доказали следующее утверждение:
Задание. Найдите площадь прямоугольника со сторонами 5 и 8 см?
Решение. Просто перемножаем эти числа:
Задание. Найдите площадь фигуры, изображенной на рисунке:
Решение. Необходимо разбить фигуры на несколько прямоугольников:
Далее считаем площадь каждого отдельного прямоугольника:
Задание. Полкомнаты необходимо покрыть паркетом. Длина и ширина комнаты равны 6 и 5,5 метрам, а каждая дощечка паркета имеет габариты 30х5 см. Сколько дощечек паркета необходимо купить для ремонта?
Решение. В таких задачах прежде всего следует все длины выразить в одних единицах измерения. Перепишем габариты комнаты:
Важно убедиться, что пол можно полностью покрыть целым числом дощечек, не используя какие-либо дощечки наполовину. Для этого габариты дощечки должны быть кратны габаритам комнаты. Это условие соблюдается:
Получается, что для покрытия пола дощечки необходимо разместить их в 20 рядов, в каждом из которых будет 110 досок. Тогда общее количество досок будет равно
Задание. Площадь прямоугольника равна 64, а одна из его сторон имеет длину 16. Найдите вторую сторону прямоугольника.
Решение. Запишем формулу площади прямоугольника:
Задание. Найдите стороны прямоугольника, если площадь равна 500, а одна из сторон в 5 раз больше другой стороны.
Решение. Обозначим меньшую сторону переменной х. Тогда большая сторона будет в 5 раз больше, то есть она равна 5х. Площадь прямоугольника будет вычисляться как произведение этих чисел
Мы получили два значения х, 10 и (– 10). Естественно, длина отрезка не может выражаться отрицательным числом, поэтому нам подходит только значение 10. Это длина меньшей стороны. Большая же сторона в 5 раз длиннее, то есть ее длина равна
Решение. Снова обозначим длину меньшей стороны буквой х, тогда большая сторона будет иметь длину х + 5 см. По условию произведение этих сторон равно 150:
Это обычное квадратное уравнение, решаемое с помощью:
Снова получили два корня, из которых только один является положительным. Итак, меньшая сторона равна 10 см. Тогда большая сторона буде равна
Решение. Обозначим смежные стороны буквами a и b. Тогда и две другие стороны также будут равны а и b. Так как периметр (его обозначают буквой Р) по определению является суммой длин всех сторон, то для прямоугольника он будет равен:
Если сюда вместо S подставить 15, а вместо а выражение 8 – b, то получим такое уравнение:
Оба полученных корня являются положительными числами, то есть устраивают нас. Зная b, легко найдем и a:
В первом случае получается, что стороны равны 3 и 5 см. Во втором случае получились те же числа, только в другом порядке: 5 и 3 см. То есть эти два ответа, по сути, идентичны друг другу.




