Что теряется при дискретизации почему
Содержание урока
§7. Дискретность
Дискретизация
§8. Алфавитный подход к оценке количества информации
§7. Дискретность
Дискретизация
Поскольку данные в компьютерах передаются с помощью дискретных сигналов, компьютеры могут хранить и обрабатывать только дискретную информацию, т. е. такую, которая может быть записана с помощью конечного количества знаков некоторого алфавита. Поэтому для ввода любых данных в компьютер их нужно перевести в дискретный код.
Дискретность означает, что мы представляем нечто целое (непрерывное) в виде набора отдельных элементов. Например, картина художника — это аналоговая (непрерывная) информация, а мозаика, сделанная на её основе (рисунок из кусочков разноцветного стекла), — дискретная. Множество вещественных чисел непрерывно (между любыми двумя различными числами есть ещё бесконечно много других), а множество целых чисел дискретно.

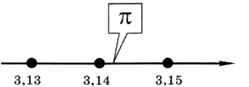
Всем известное иррациональное число л содержит бесконечное количество знаков в дробной части. Если мы хотим записать, чему равно π, необходимо остановиться на каком-то знаке, отбросив остальные, например: π ≈ 3,14. Таким образом, мы перешли к дискретной информации, потому что рассматриваем только числа с шагом 0,01 — точки на числовой оси (рис. 2.10).
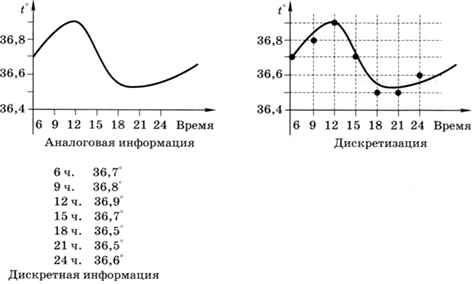
Изменение высоты столбика термометра — это аналоговая информация, а записанная температура, округлённая до десятых долей градуса (например, 36,6°), — дискретная (рис. 2.11).
Дискретность состоит в том, что записанные значения температуры изменяются скачкообразно (через 0,1°), — это дискретизация по уровню, или квантование. Кроме того, обычно температуру больного измеряют не непрерывно, а несколько раз в день — появляется дискретизация по времени.
Заметим, что при дискретизации, как правило, происходит потеря информации. В данном случае мы, во-первых, потеряли информацию об изменении температуры между моментами измерений и, во-вторых, исказили измеренные значения, округлив их до десятых (каждая дискретизация, и по времени, и по уровню, вносит свою ошибку). Чтобы уменьшить ошибки, нужно уменьшить шаг дискретизации — измерять температуру чаще, записывать показания термометра до тысячных долей градуса. Однако в любой практической задаче есть некоторый предел, после которого увеличение точности уже никак не влияет на конечный результат.
Из приведённого примера понятно, что непрерывность или дискретность — это не свойство самой информации, а свойство её представления. В данном случае информация — это сведения об изменении температуры человека в течение дня. Если бы температура измерялась постоянно и записывалась самописцем (в виде графика), можно было бы говорить о том, что информация представлена в аналоговой (непрерывной) форме.
Ещё один пример — аналоговые («стрелочные») и цифровые вольтметры, которые измеряют одну и ту же величину, но выводят результат измерения в разном виде (рис. 2.12).
Теперь подумаем, как записать аналоговую величину, которая может принимать бесконечное множество значений. Вы уже знаете, что с помощью алфавита, состоящего из N символов, можно закодировать Q = разных сообщений длины L. Поэтому теоретически для записи аналоговой величины придется использовать бесконечное число знаков.
Итак, когда мы хотим записать (зафиксировать) информацию с помощью какого-то алфавита, нужно переходить к дискретному представлению. С одной стороны, это делает более надёжной передачу данных (если обе стороны одинаково понимают используемые знаки). С другой стороны, при дискретизации часть информации теряется.
Хотя аналоговую информацию невозможно точно представить в дискретном виде, при увеличении точности дискретизации свойства непрерывной и дискретной информации практически совпадают. Например, для точной записи числа тг требуется бесконечное количество цифр, но в расчётах чаще всего достаточно знать это значение с точностью не более 10 знаков.
Идеальная непрерывность существует только в теории. Мы считаем дерево, пластмассу, металл непрерывными, но на самом деле они состоят из отдельных молекул, расположенных на некотором расстоянии друг от друга, — это значит, что вещество дискретно. Иллюстрация в книге кажется нам сплошной, но при сильном увеличении видно, что она строится из отдельных точек (имеет «растр») (рис. 2.13).
«Плёночная» фотография считается аналоговой, но при увеличении снимка с фотоплёнки нельзя бесконечно получать все новые и новые детали — предел «уточнения» определяется величиной зерна светочувствительного материала.
Мы часто воспринимаем дискретные объекты как непрерывные, потому что наши органы чувств не позволяют различить отдельные элементы. Например, разрешающая способность глаза составляет около одной угловой минуты (1′ = 1/60 часть градуса), это значение определяется размером элементов сетчатки глаза. Поэтому человек не может различить два объекта, если направления на них различаются меньше, чем на 1′. Для того чтобы повысить разрешающую способность при наблюдении, применяют специальные приборы (например, бинокли и микроскопы).
Следующая страница 
Cкачать материалы урока
Что теряется при дискретизации почему
2.2. Оцифровка звука
Оцифровка − процесс преобразования аналогового сигнала в цифровой.
Дискретизация и квантование могут выполняться в произвольном порядке. Эти процессы выполняются специальными устройствами, которые обобщенно называются аналого-цифровыми преобразователями (АЦП).
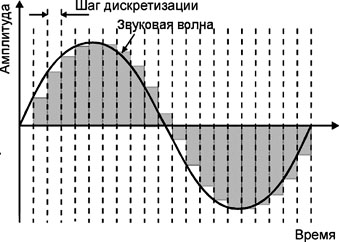
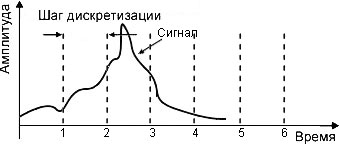
Процесс дискретизации − это процесс получения значений величин преобразуемого сигнала в определённые промежутки времени (рис. 2.5). Как видно из рис. 2.5-2.6, в процессе оцифровки часть информации теряется. Если частота дискретизации слишком мала, тогда в процессе оцифровки некоторые детали будут утрачены. Например, при дискретизации сигнала (рис. 2.6) с недостаточной частотой мы попросту пропустим пик между точками 2 и 3, а при восстановлении аналогового сигнала по полученным дискретным значениям сигнал будет сильно отличаться от оригинала. Так как же выбрать правильную частоту дискретизации в процессе оцифровки?
Рис. 2.6. Дискретизация с недостаточной частотой
Согласно теореме о дискретном представлении [10], если самая высокая частота из частот компонентов сигнала равна fh, то сигнал можно будет точно восстановить в том случае, если его дискретизация была выполнена с частотой, превышающей 2fh. Это граничное значение известно под названием частота Найквиста.
Доказательство теоремы можно очень просто проиллюстрировать. Предположим, имеется круглый диск со стрелкой, которая вращается по часовой стрелке со скоростью n оборотов в секунду. Предположим также, что это вращение оцифровывается с разной частотой дискретизации 4n, n, 4/3n, 2n раз в секунду.
Посмотрев ролики (рис. 2.7), можно увидеть, что при частоте дискретизации 4n, которая больше частоты Найквиста, диск вращается по часовой стрелке, как нам и надо. При дискретизации с частотой 4n/3 кажется, что стрелка вращается против часовой стрелки со скоростью n/3. А если выполнять дискретизацию движения нашего диска с частотой, равной 2n, то можно не определить, в какую сторону вращается стрелка, так как она будет находиться либо вверху, либо внизу.
Вывод: частота дискретизации должна превышать частоту Найквиста.
Рис. 2.7. Flash-ролик вращающейся стрелки, дискретизированной с разной частотой n (для просмотра и остановки щелкните на кнопку «пуск»)
Что теряется при дискретизации почему
Вопрос: Расскажите подробнее о дискретизации и квантовании цифрового сигнала.
Ответ: 4 В последнее время в технике идет переход на цифровые методы обработки информации. Это связано с тем, что цифровую информацию легче хранить (появились дешевые и удобные устройства для хранения информации, такие как жесткие диски компьютеров или лазерные диски), а также с тем, что цифровую информацию легко передавать по современным линиям связи практически без потерь.
Приведем конкретный пример дискретизации и квантования:
| = | 0. | 0.3162. | 0.4472. | 0.5477. | 0.6324. | . |
| = | 0 | 0.1 | 0.2 | 0.3 | 0.4 | . |
Учитывая точность хранения значений x, после квантования получаем
| = | 0. | 0.32. | 0.45. | 0.55. | 0.63. | . |
| = | 0 | 0.1 | 0.2 | 0.3 | 0.4 | . |
Для примера, описанного выше, имеем
| = | 0. | 0.3162. | 0.4472. | 0.5477. | 0.6324. | . |
| = | 0. | 0.32. | 0.45. | 0.55. | 0.63. | . |
| = | 0 | 0.1 | 0.2 | 0.3 | 0.4 | . |
| шум квантования | 0. | 0.00377 | 0.00279 | 0.00228 | 0.00246 | . |
Устройство, производящее обратную операцию (чтобы передать оцифрованный сигнал на какое-нибудь воспроизводящее устройство (динамик, телевизор, приводной мотор и т.д.)) называется цифро-аналоговым преобразователем (ЦАП). Принципиальные схемы АЦП и ЦАП следует искать в книжках по радиоэлектронике (о принципах работы некоторых схем смотри в [1]).
Цифровую информацию можно передать по линии связи практически без потерь. При передаче сигнал сначала превращается в аналоговый, пересылается, после чего опять оцифровывается. Если линия связи вносит искажения в сигнал меньше чем шаг квантования, то после передачи и оцифровки полученный оцифрованный сигнал не будет отличаться от начального. Обычно же информация передается с помощью двоичных импульсов, т.е. для восстановления сигнала необходимо лишь решать, передали 1 или 0. При передаче двоичной информации по линии связи естественно слегка смещается время прибытия импульса, но если смещение меньше расстояния между импульсами, то место импульса в общей последовательности легко восстанавливается. Дополнительную защиту дает применение кодов с устранением ошибок (коды Хэмминга, Рида-Соломона и др.).
MT1402: Теоретические основы информатики. Имитационное моделирование
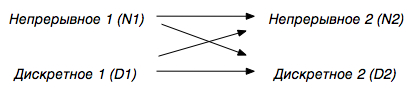
Поскольку имеются два типа сообщений, между ними, очевидно, возможны четыре варианта преобразований:
Осуществимы и применяются на практике все четыре вида преобразований. Рассмотрим примеры устройств и ситуаций, связанных с такими преобразованиями, и одновременно попробуем отследить, что при этом происходит с информацией.
Примерами устройств, в которых осуществляется преобразование типа %%N_1 → N_2%%, являются микрофон (звук преобразуется в электрические сигналы); магнитофон и видеомагнитофон (чередование областей намагничения ленты превращается в электрические сигналы, которые затем преобразуются в звук и изображение); телекамера (изображение и звук превращаются в электрические сигналы); радио-и телевизионный приемник (радиоволны преобразуются в электрические сигналы, а затем в звук и изображение); аналоговая вычислительная машина (одни электрические сигналы преобразуются в другие).
Особенностью данного варианта преобразования является то, что оно всегда сопровождается частичной потерей информации.
Потери связаны с помехами (шумами), которые порождает само информационное техническое устройство и которые воздействуют извне. Эти помехи примешиваются к основному сигналу и искажают его. Поскольку параметр сигнала может иметь любые значения (из некоторого интервала), то невозможно отделить ситуации: был ли сигнал искажен или он изначально имел такую величину. В ряде устройств искажение происходит в силу особенностей преобразования в них сообщения, например в черно-белом телевидении теряется цвет изображения; телефон пропускает звук в более узком частотном интервале, чем интервал человеческого голоса; кино- и видеоизображение оказываются плоскими, они утратили объемность.
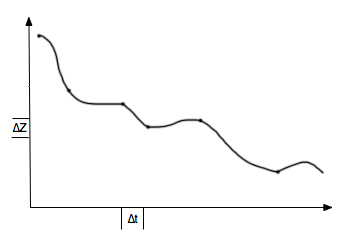
Подобное преобразование называется дискретизацией непрерывного сигнала и осуществляется посредством двух операций: развертки по времени и квантования по величине сигнала.
Совместное выполнение обеих операций эквивалентно нанесению масштабной сетки на график %%Z(t)%%, как показано на рис.1.2. Далее, в качестве пар значений %%
Рис.1-2. Дискретизация аналогового сигнала за счет операций развертки по времени и квантования по величине
Ответом на эти сомнения служит так называемая теорема отсчетов, доказанная в 1933 г. В. А. Котельниковым (по этой причине ее иногда называют его именем), значение которой для решения проблем передачи информации было осознано лишь в 1948 г. после работ К. Шеннона. Теорема, которую примем без доказательства, но результаты будем в дальнейшем использовать, гласит:
Непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений или отсчетов величины этого сигнала через одинаковые интервалы времени, меньшие или равные половине периода максимальной частоты, имеющейся в сигнале.
Комментарии к теореме:
Теорема касается только тех линий связи, в которых для передачи используются колебательные или волновые процессы. Это не должно восприниматься как заметное ограничение, поскольку действие большинства практических устройств связи основано именно на этих процессах.
Можно перефразировать теорему отсчетов:
Развертка по времени может быть осуществлена без потери информации, связанной с особенностями непрерывного (аналогового) сигнала, если шаг развертки не будет превышать %%∆t%%, определяемый в соответствии с (1.1).
Например, для точной передачи речевого сигнала с частотой до %%v_m = 4000%% Гц при дискретной записи должно производиться не менее 8000 отсчетов в секунду; в телевизионном сигнале %%v_m = 4%% МГц, следовательно, для его точной передачи потребуется около 8000000 отсчетов в секунду.
Приходим к заключению, что шаг квантования определяется чувствительностью приемного устройства.
Указанные соображения по выбору шага развертки по времени и квантования по величине сигнала лежат в основе оцифровки звука и изображения. Примерами устройств, в которых происходят такие преобразования, являются сканер, модем, устройства для цифровой записи звука и изображения, лазерный проигрыватель, графопостроитель.
Термины «цифровая запись», «цифровой сигнал» следует понимать как дискретное представление с применением двоичного цифрового алфавита.
Таким образом, преобразование сигналов типа %%N → D%%, как и обратное %%D → N%%, может осуществляться без потери содержащейся в них информации.
Примерами ситуаций, в которых осуществляются подобные преобразования, могут быть: запись-считывание с компьютерных носителей информации; шифровка и дешифровка текста; вычисления на калькуляторе.
Таким образом, за исключением %%N_1 → N_2%% в остальных случаях оказывается возможным преобразование сообщений без потерь содержащейся в них информации. При этом на первый взгляд непрерывные и дискретные сообщения оказываются равноправными. Однако на самом деле это не так. Сохранение информации в преобразованиях %%N → D%% и %%D → N%% обеспечивается именно благодаря участию в них дискретного представления. Другими словами, преобразование сообщений без потерь информации возможно только в том случае, если хотя бы одно из них является дискретным. В этом проявляется несимметричность видов сообщений и преимущество дискретной формы. К другими ее достоинствам следует отнести:
Отсюда становится понятной приоритетность дискретной формы представления информации по отношению к непрерывной в решении глобальной задачи автоматизации обработки информации. Приведенные в данном параграфе соображения позволяют нам в дальнейшем исследовать только дискретную информацию, а для ее представления (фиксации) использовать некоторый алфавит. При этом нет необходимости рассматривать физические особенности передачи и представления, т.е. характер процессов и виды сигналов. Полученные результаты будут справедливы для любой дискретной информации независимо от реализации сообщения, с которым она связана. С этого момента и начинается наука информатика.
Дискретизация
Что такое дискретизация в информатике
Для того чтобы решить определенные задачи, человек вынужден преобразовывать имеющуюся информацию из одной формы, в которой она представлена, в другую. Например, при чтении книги вслух мы преобразовываем информацию из текстовой (дискретной) формы в звуковую (непрерывную). Тот, кто занимается транскрибацией, преобразовывает звуковую форму в текстовую — совершает обратный процесс.
Для того чтобы передавать, хранить, автоматически обрабатывать данные, гораздо удобнее использовать дискретную форму представления информации. В этом и состоит ее основное преимущество. Именно поэтому информатика — наука, на которой основана работа всей компьютерной техники, — много внимания уделяет дискретизации.
Дискретизация — процесс, с помощью которого непрерывная форма представления информации преобразуется в дискретную.иеие
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В информатике под понятием дискретности подразумевают алгоритм решения задачи, разбивающий весь процесс на определенное количество простых шагов (этапов), выполняемых поочередно.
Другими словами, дискретность — это набор действий, имеющих строго определенную, предписанную им алгоритмом последовательность. Каждое следующее действие может быть исполнено только при полном завершении предыдущего этапа.
Формы представления дискретной информации
Итак, существуют две формы представления информации:
Они принципиально отличаются в зависимости от своей природы.
Любой объект или явление, существующие в нашем мире, можно представить с помощью определенных физических величин и характеристик. Такое природное явление, как циклон, можно описать с помощью скорости ветра, температуры воздуха, количества выпавших осадков и другими характерными для циклона величинами.
Характерные физические величины для описания человека:
Все вышеуказанные физические величины имеют собственные определенные диапазоны. Количество значений, которые способна принимать та или иная величина, может быть бесконечным.
Подобные величины и ту информацию, которую они передают, принято называть непрерывными. Между значениями таких величин не бывает скачкообразных разрывов. Такая непрерывная величина, как масса тела, например, может принимать любые значения от нуля до бесконечности, включая дробные.
Кроме непрерывных величин, существуют и такие, которые обозначают целое, а не дробное количество: например, число музыкантов в оркестре или число атомов в молекуле вещества.
Если объект изучения обладает характерным свойством в какие-то моменты принимать строго конкретные значения (знаковые или числовые), то это свойство называют дискретной информацией об объекте.
Особенность дискретной информации — ее прерывистость, возможность пронумеровать и представить в цифровом виде с использованием логических нуля и единицы.
Дискретными значениями являются:
Для того чтобы обладать наиболее полными сведениями об объекте или явлении, чаще всего их описывают с помощью двух форм представления информации одновременно.
Геометрическую фигуру можно описать с помощью ее дискретного значения (квадрат) и непрерывного значения длины его стороны (15,25 см).
При использовании пружинных весов или весов со стрелкой измеряемая величина (масса) является сама по себе непрерывной. Но весы переводят этот показатель в дискретную форму в зависимости от того, к какому делению шкалы ближе окажется бегунок пружинных весов или стрелка.
В этом случае, чем более мелкие деления на шкале, тем более точной будет дискретное представление информации о массе взвешиваемого предмета.
Дискретную информацию принято представлять в символьном виде, с использованием знаков — натуральных чисел или букв. С помощью натуральных чисел можно представить деления на шкале измерительного прибора, нумерацию страниц книги или домов на улице города.
Цифровой вариант представления информации очень удобен для использования в ЭВМ.
В повседневной жизни для представления информации помимо цифр используют слова, составленные из букв какого-либо алфавита (русского, латинского, китайского и пр.). С помощью слов обозначают имена и свойства объектов, перечисляют действия.
Также широкое применение получили различные математические символы, знаки препинания.
Использование совокупности всех имеющихся символов, условно именуемой «алфавитом», дает возможность создания различных информационных объектов.
Такой вид представления информации называется символьным, так как она имеет дискретную природу, заключенную в использовании последовательности различных символов.
Существует большое количество «алфавитов» или систем письменности, с помощью которых можно передать (записать, сохранить) одну и ту же информацию различными символическими наборами.
В качестве примера поставим в соответствие каждой букве алфавита ее порядковый номер. В этом случае с помощью цифр от 0 до 9 можно записать текст целой книги.
Более того, ту же самую информацию можно закодировать с помощью двоичного кода, используя всего 2 символа — 0 и 1.
К дискретным формам представления информации относят также ее графическое изображение в виде различных чертежей, графиков, схем.
Информационные параметры сигнала
Дискретизация в системах обработки информации выглядит как обмен информацией, который происходит с помощью сигналов. Носителями таких сигналов выступают физические величины, которые могут быть представлены распределением сигналов в пространстве и времени.
Показатели соответствующих временных функций являются информационными параметрами сигнала. Среди таких показателей могут быть:
Как происходит дискретизация, основные этапы
По аналогии с видом представления информации сигналы классифицируют также на 2 типа:
В случае аналогового сигнала параметры внутри отдельных диапазонов могут принимать любые значения в любой момент времени.
В случае дискретного сигнала каждому установленному моменту времени соответствует определенное значение параметра. Дискретный сигнал описывает непрерывную информацию в виде точек графика, построенного в системе координат. В ней ось абсцисс представляет собой время сигнала в дискретном изображении, а ось ординат отражает дискретное представление уровня сигнала.
Преобразование аналогового сигнала в дискретный называется дискретизацией, которая происходит как по времени, так и по уровню сигнала.
Рассмотрим, как происходит дискретизация на примере самописцев атмосферного давления. Эти приборы работают на метеорологических станциях. Они в непрерывном режиме записывают изменение атмосферного давления на протяжении длительного времени в виде барограмм — кривых, вычерченных прибором в течение нескольких часов.
Одна из таких барограмм представлена ниже:
Взяв график за основу, можно снять с него необходимую нам информацию. Например, показания самописца в начале измерения атмосферного давления и каждый последующий час. Полученные данные заносятся в таблицу:
Таким образом, мы смогли преобразовать полученную в аналоговой (непрерывной) форме информацию в дискретный вид.
Если внимательно сравнить данные таблицы с данными графика, то можно заметить некоторую потерю точности. Так, самого большого значения давление достигло во время четвертого часа работы самописца, но в таблицу эта информация не попала.
Чтобы увеличить точность процесса дискретизации, следует брать меньшие временные интервалы. Например, снимать данные с барограммы не раз в час, а каждые полчаса или пятнадцать минут. В этом случае мы получим более точную картину изменения давления, представленную в дискретной форме.
Дискретные сигналы легче обрабатывать и хранить, чем аналоговые. Кроме того, на них практически не влияют помехи во время передачи на большие расстояния, что является их явным преимуществом. Поэтому использование дискретных сигналов получило более широкое распространение по сравнению с непрерывными.
Побочные эффекты дискретизации и квантования
Как мы уже выяснили, дискретизация происходит как по уровню (амплитуде) сигнала, так и по времени. При этом дискретизацию по уровню часто называют квантованием. В научной литературе могут встречаться оба термина, которые обозначают процесс оцифровки сигнала.
Поскольку все сигналы в природе имеют аналоговое происхождение, то для их хранения, обработки и передачи необходимо сначала оцифровывать сигналы — произвести с помощью аналого-цифровых приборов их дискретизацию и квантование по уровню.
После этого любой сигнал можно закодировать, провести его цифровую обработку, передать на расстоянии и хранить. При этом часто возникает необходимость преобразовать полученный цифровой сигнал обратно в аналоговый.
Подобным образом, например, происходит звуковое воспроизведение аудиозаписей с компакт-дисков. Цифровые сигналы, записанные в области высоких частот, преобразуются в низкочастотные звуковые.
Обратное преобразование сигнала происходит с определенной степенью точности, которая зависит от:
Следует учесть, что чем больше будет частота и число уровней, тем больше будет и цифровой информации, а значит, потребуется соответствующее количество ресурсов для ее передачи, хранения, обработки. Поэтому приходится соблюдать разумный компромисс между желаемой точностью воспроизведения сигнала и размерами обеспечивающих ее ресурсов.