что такое условный экстремум

Метод множителей Лагранжа.

Рассмотрим функцию \(n+m\) переменных
$$
L(x, \lambda) = f_<0>(x)+\lambda_<1>f_<1>(x)+\ldots+\lambda_f_(x),\nonumber
$$
где \(x \in G\), а \(\lambda = (\lambda_<1>, \ldots, \lambda_) \in \boldsymbol^\). Числа \(\lambda_<1>, \ldots, \lambda_\) называются множителями Лагранжа, а функция \(L(x, \lambda)\) называется функцией Лагранжа.

Пусть \(x^<0>\) — точка условного экстремума функции \(f_<0>(x)\) при наличии связей \eqref, и пусть функции \(f_(x)\), \(i = \overline<0, m>\), непрерывно дифференцируемы в окрестности точки \(x^<0>\), причем в точке \(x^<0>\) ранг матрицы Якоби
$$
A = \begin\displaystyle\frac<\partial f_<1>><\partial x_<1>>(x)&\ldots&\displaystyle\frac<\partial f_<1>><\partial x_>(x)\\………&…..&…….\\\displaystyle\frac<\partial f_><\partial x_<1>>(x)&\ldots&\displaystyle\frac<\partial f_><\partial x_>(x)\end\label
$$
равен \(m\).

Тогда найдутся такие множители Лагранжа \(\lambda_<1>^<0>, \ldots, \lambda_^<0>\), что \((x^0,\ \lambda^0)\) будет стационарной точкой функции Лагранжа.

\(\circ\) Так как \(m Теорема 2.

Пусть \(x^<0>\) есть точка условного минимума функции \(f_<0>(x)\) при наличии связей \eqref, и пусть функции \(f_(x)\), \(i = \overline<1, m>\), имеют непрерывные частные производные второго порядка в окрестности точки \(x^<0>\), причем в точке \(x^<0>\) ранг функциональной матрицы \eqref равен \(m\).

Тогда найдутся множители Лагранжа \(\lambda_<1>^<0>, \ldots, \lambda_^<0>\) такие, что \((x^<0>, \lambda^<0>)\) есть стационарная точка функции Лагранжа, a \(d^<2>L(x^<0>, \lambda^<0>) \geq 0\) при \((dx_<1>, \ldots, dx_) \in E_\).

\(\circ\) Так как выполнены все условия теоремы 1, то найдутся множители Лагранжа \(\lambda_<1>^<0>, \ldots, \lambda_^<0>\) такие, что \((x^<0>, \lambda^<0>)\) будет стационарной точкой функции Лагранжа, то есть выполняются условия \eqref. Повторяя рассуждения теоремы 1, рассмотрим сложную функцию \eqref, имеющую безусловный экстремум в точке \((x_^<0>, \ldots, x_^<0>)\). Так как эта функция имеет непрерывные частные производные второго порядка, то, в силу теоремы о необходимом условии минимума должно быть выполнено условие \(d^<2>F(x_^<0>, \ldots, x_^<0>) \geq 0\).

Воспользовавшись правилом нахождения второго дифференциала сложной функции и формулой \eqref, находим, что
$$
\sum_^ \sum_^ \frac <\partial^<2>f_<0>(x^<0>)> <\partial x_\partial x_> dx_ dx_+\sum_^ \frac <\partial^<2>f_<0>><\partial x_>(x^<0>) d^<2>x_ \geq 0.\label
$$

Если умножить каждое из равенств \eqref на соответствующий множитель Лагранжа \(\lambda_^<0>\) и сложить с неравенством \eqref, то получаем неравенство
$$
d_^<2>L(x^<0>, \lambda^<0>)+\sum_^ \frac<\partial L(x^<0>, \lambda^<0>)><\partial x_> d^<2>x_ \geq 0.\label
$$
Последняя сумма в неравенстве \eqref равна нулю, так как \((x^<0>, \lambda^<0>)\) есть стационарная точка функции Лагранжа и в ней выполняются условия \eqref. Таким образом, \(d_^<2>L(x^<0>, \lambda^<0>) \geq 0\) при \((dx_<1>, \ldots, dx_) \in E_\). \(\bullet\)

(Достаточные условия условного экстремума).

Пусть функции \(f_(x)\), \(i = \overline<0, m>\), имеют непрерывные частные производные второго порядка в окрестности точки \(x^ <0>\in \boldsymbol^\), причем в точке \(x^<0>\) ранг функциональной матрицы (3) равен \(m\), и пусть \((x^<0>, \lambda^<0>)\) есть стационарная точка функции Лагранжа \(L(x, \lambda)\).

Тогда если \(d_L(x^<0>, \lambda^<0>)\) есть положительно определенная квадратичная форма при \(dx \in E_\), то \(x^<0>\) является точкой условного строгого минимума функции \(f_<0>(x)\) при наличии связей \eqref. Если \(d_L(x^<0>, \lambda^<0>)\) есть отрицательно определенная квадратичная форма при \(dx \in E_\), то \(x^<0>\) — точка условного строгого максимума. Если \(d_L(x^<0>, \lambda^<0>)\) есть неопределенная квадратичная форма при \(dx \in E_\), то \(x^<0>\) не есть точна условного экстремума функции \(f_<0>(x)\) при наличии связей \eqref.

\(\circ\) Пусть
$$
E = \(x) = 0, i = \overline<1, m>\>.\label
$$
По условию теоремы функции \(f_(x)\), \(i = \overline<0, m>\), имеют непрерывные частные производные второго порядка, а ранг функциональной матрицы \eqref равен \(m\). Повторяя рассуждения теоремы 1, можем без ограничения общности считать, что выполнено условие \eqref и что найдется такая окрестность \(K(x^<0>) = K_<1>(x_<1>^<0>, \ldots, x_^<0>) \times K_<2>(x_^<0>, \ldots, x_^<0>)\), что множество \(E \cap K(x^<0>)\) можно задать формулой \eqref. На \(E \cap K(x^<0>)\) функция \(f_<0>(x)\) становится функцией \(n-m\) переменных \(F(x_^<0>, \ldots, x_^<0>)\), определенной формулой \eqref и имеющей непрерывные частные производные второго порядка.

Рассмотрим функцию \(L(x, \lambda^<0>)\) на множестве \(E \cap K(x^<0>)\). Очевидно, что
$$
L(x, \lambda^<0>) = f_<0>(x) = F(x_, \ldots, x_)\ \mbox<при>\ x \in E \cap K(x^<0>).\label
$$
В силу инвариантности формы первого дифференциала из формулы \eqref следует, что
$$
dF(x_^<0>, \ldots, x_^<0>) = d_L(x^<0>, \lambda^<0>) = 0.\label
$$

Пусть \(d_^<2>L(x^<0>, \lambda^<0>) > 0\) при \(dx \in E_\), \(dx \neq 0\). Так как множество \(E \cap K(x^<0>)\) можно задать в форме \eqref, то, выбирая \(dx_, \ldots, dx_\) произвольным образом, получим, что дифференциалы \(dx_<1>,…, dx_\) зависят от \((dx_, \ldots, dx_)\). Дифференцируя тождества \eqref в точке \(x^<0>\), получаем соотношения \eqref, которые означают, что \(dx \in E_\).

Из \eqref и \eqref получаем, что \((x_^<0>, \ldots, x_^<0>)\) есть точка строгого минимума функции \(F(x_, \ldots, x_)\), то есть \(x^<0>\) есть точка строгого минимума функции \(f_<0>(x)\) на множестве \(E \cap K(x^<0>)\). Таким образом, \(x^<0>\) есть точка строгого условного минимума функции \(f_<0>(x)\) при наличии связей \eqref.

Аналогично рассматривается случай, когда \(d_^<2>L(x^<0>, \lambda^<0>) Замечание.

Если окажется, что \(d_^<2>L(x^<0>, \lambda^<0>)\) есть положительно определенная квадратичная форма на всем пространстве \(\boldsymbol^\), то \(d_^<2>L(x^<0>, \lambda^<0>) > 0\) при \(dx \in E_\), \(dx \neq 0\). Поэтому в этом случае в квадратичной форме \(d_^<2>L(x^<0>, \lambda^<0>)\) не нужно исключать зависимые дифференциалы.

Найти экстремумы функции \(x-2y+2z = u\) и на сфере \(x^<2>+y^<2>+z^ <2>= 1\).

Найти условные экстремумы функции \(f_<0>(x, y) = e^\), \(a \neq 0\), при наличии ограничения \(f_(x, y) = x^<3>+y^<3>+x+y-4 = 0\).

\(\vartriangle\) Построим функцию Лагранжа:
$$
L(x, y) = e^+\lambda(x^<3>+y^<3>+x+y-4).\nonumber
$$
Стационарные точки функции Лагранжа определяются из системы уравнений
$$
\begin
& \displaystyle\frac<\partial L> <\partial x>= aye^+\lambda(3x^<2>+1) = 0,\\
&\\
& \displaystyle\frac<\partial L> <\partial y>= axe^+\lambda(3y^<2>+1) = 0,\\
&\\
& \displaystyle\frac<\partial L> <\partial \lambda>= x^<3>+y^<3>+x+y-4 = 0.
\end\label
$$

Умножая первое уравнение на \(x\), а второе на \(y\) и вычитая, получаем
$$
\lambda(3x^<3>-3y^<3>+x-y) = \lambda(x-y)(3x^<2>+3xy+3y^<2>+1) = 0.\label
$$

Поэтому при \(a 0\) — условный максимум функции \(f_<0>(x, y)\) при наличии связи \(x^<3>+y^<3>+x+y = 4\), причем экстремальное значение функции равно \(e^\). \(\blacktriangle\)

Уравнение связи \(x^<3>+y^<3>+x+y = 4\) было бы затруднительно разрешить относительно одной из переменных. Метод Лагранжа для примера 2 более эффективен, чем прямой метод исключения зависимых переменных.

Несколько замечаний о методе множителей Лагранжа.

Задачи об отыскании экстремумов функций (как числовых, так и функций более общей природы) при наличии ограничений являются весьма распространенными. Теория экстремальных задач интенсивно развивается и находит широкий круг приложений. Здесь были рассмотрены ограничения типа равенств, задаваемые достаточно гладкими функциями (гладкие связи). Метод множителей Лагранжа имеет глубокие обобщения и на более общий случай, когда ограничения задаются системой равенств и неравенств при помощи недифференцируемых в обычном смысле функций.

В конкретных прикладных вопросах множители Лагранжа имеют содержательную интерпретацию. Так, в механике множители Лагранжа задают реакции связей, а в математической экономике — цены на продукты производства. Широко развиты приближенные методы решения экстремальных задач, использующие современную вычислительную технику.

Источник

Условный экстремум

где λ_i – некоторые постоянные, называется функцией Лагранжа, а числа λ_i – неопределенными множителями Лагранжа.

Теорема 5.3 (необходимые условия условного экстремума). Условный экстремум функции z = f (x, y) при наличии уравнения связи φ (х, у) = 0 может достигаться только в стационарных точках функции Лагранжа L (x, y) = f (x, y) + λφ (x, y).

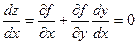
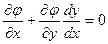
Доказательство. Уравнение связи задает неявную зависимость у от х, поэтому будем считать, что у есть функция от х: у = у(х). Тогда z есть сложная функция от х, и ее критические точки определяются условием: . (5.4) Из уравнения связи следует, что . (5.5)

Умножим равенство (5.5) на некоторое число λ и сложим с (5.4). Получим:

, или .

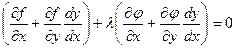
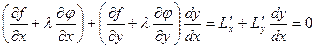
Последнее равенство должно выполняться в стационарных точках, откуда следует:

(5.6)

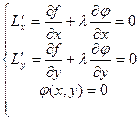
Получена система трех уравнений относительно трех неизвестных: х, у и λ, причем первые два уравнения являются условиями стационарной точки функции Лагранжа. Исключая из системы (5.6) вспомогательное неизвестное λ, находим координаты точек, в которых исходная функция может иметь условный экстремум.

Замечание 1. Проверку наличия условного экстремума в найденной точке можно провести с помощью исследования частных производных второго порядка функции Лагранжа по аналогии с теоремой 5.2.

Пример. Найдем условный экстремум функции z = xy при условии х + у = 1. Составим функцию Лагранжа L(x, y) = xy + λ (x + y – 1). Система (5.6) при этом выглядит так:

Источник

Условный экстремум

Пусть — открытое множество и на заданы функции . Пусть .

Эти уравнения называют уравнениями связей (терминология заимствованна из механики).

Пусть на G определена функция . Точка называется точкой условного экстремума функции относительно уравнений связи, если она является точкой обычного экстремума на множестве E (рассматриваются окрестности ).

Содержание

Метод множителей Лагранжа для решения задачи условного экстремума

Теорема

Пусть — точка условного экстремума функции при выполнении уравнений связи. Тогда в этой точке градиенты являются линейно зависимыми, то есть но .

Следствие

Если — точка условного экстремума функции относительно уравнений связи, то такие, что в точке или в координатном виде .

Достаточное условие условного экстремума

Пусть является стационарной точкой функции Лагранжа при . Если — отрицательно (положительно) определена квадратическая форма переменных при условии , то является точкой max (min для положительно определенной) условного экстремума. Если она при этих условиях не является знакоопределенной, тогда экстремума нет.

См. также

Полезное

Смотреть что такое «Условный экстремум» в других словарях:

Условный экстремум — относительный экстремум, экстремум функции f (x1. xn + m) от п + т переменных в предположении, что эти переменные подчинены ещё т уравнениям связи (условиям): φk (x1. xn + m) = 0, 1≤ k ≤ m (*) (см. Экстремум).… … Большая советская энциклопедия

УСЛОВНЫЙ ЭКСТРЕМУМ — минимальное или максимальное значение, достигаемое данной функцией (или функционалом) при условии, что нек рые другие функции (функционалы) принимают значения из заданного допустимого множества. Если условия, ограничивающие в указанном смысле… … Математическая энциклопедия

Экстремум — (от лат. extremum крайнее) значение непрерывной функции f (x), являющееся или максимумом, или минимумом. Точнее: непрерывная в точке х0 функция f (x) имеет в x0 максимум (минимум), если существует окрестность (x0 + δ, x0 δ) этой точки,… … Большая советская энциклопедия

Экстремум — У этого термина существуют и другие значения, см. Экстремум (значения). Экстремум (лат. extremum крайний) в математике максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум,… … Википедия

ЛАГРАНЖА ФУНКЦИЯ — функция, используемая при решении задач на условный экстремум функций многих переменных и функционалов. С помощью Л. ф. записываются необходимые условия оптимальности в задачах на условный экстремум. При этом не требуется выражать одни переменные … Математическая энциклопедия

Вариационное исчисление — математическая дисциплина, посвященная отысканию экстремальных (наибольших и наименьших) значений функционалов переменных величин, зависящих от выбора одной или нескольких функций. В. и. является естественным развитием той главы… … Большая советская энциклопедия

ЛАГРАНЖА МНОЖИТЕЛИ — переменные, с помощью к рых строится Лагранжа функция при исследовании задач на условный экстремум. Использование Л. м. и функции Лагранжа позволяет единообразным способом получать необходимые условия оптимальности в задачах на условный экстремум … Математическая энциклопедия

Вариационное исчисление — Вариационное исчисление это раздел функционального анализа, в котором изучаются вариации функционалов. Самая типичная задача вариационного исчисления состоит в том, чтобы найти функцию, на которой заданный функционал достигает… … Википедия

Вариационное исчесление — Вариационное исчисление это раздел математики, в котором изучаются вариации функционалов. Самая типичная задача вариационного исчисления состоит в том, чтобы найти функцию, на которой функционал достигает экстремального значения. Методы… … Википедия

Источник

Условные экстремумы и функция Лагранжа

В задачах оптимизации возникает необходимость найти экстремумы функции двух и более переменных при условии, что существует связь между переменными этой связи, заданная уравнением . В этом случае говорят, что требуется найти условный экстремум.

Для того чтобы найти условный экстремум требуется находить частные производные и решать системы уравнений Существует алгоритм нахождения условного экстремума из трёх шагов, который сейчас и разберём на примере, и геометрический смысл условного экстремума, который должен дойти до каждого при разборе этого самого примера.

Шаг 1. Вводится функция Лагранжа

,

Пример 1. Найти условные экстремумы функции двух переменных , выражающей площадь прямоугольника через его стороны x и y при условии , означающем, что существует верёвка, которой можно ограничить этот прямоугольник, и длина этой верёвки равна 100.

Шаг 1. Решение. Приведём уравнение условия связи к требуемому виду с нулём в правой части:

.

Составим функцию Лагранжа:

.

Шаг 2. Составляем систему уравнений из равенств частных производных нулю и уравения условия связи (необходимый признак существования условного экстремума):

Решение. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y :

Подставим эти выражения в третье уравнение и найдём значение множителя Лагранжа:

Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции:

Получили и . Эти значения являются также координатами стационарной точки. Таким образом, получили стационарную точку .

Шаг 3. Пусть является стационарной точкой, найденной на шаге 2. Чтобы определить, является ли условный экстремум минимумом или максимумом, нужно найти второй дифференциал функции Лагранжа

и в полученном выражении подставить вместо «лямбды» её значения (значения множителя Лагранжа), найденные на шаге 2.

Если значение второго дифференциала функции Лагранжа меньше нуля (), то стационарная точка является точкой максимума, если больше нуля (), то стационарная точка является точкой минимума. Если значение второго дифференциала функции Лагранжа равно нулю, то требуются дополнительные исследования, но такие случаи практически не попадаются в задачах, задаваемых студентам.

Координаты стационарных точек подставляются в исходную точку и, таким образом, мы окончательно находим условные экстремумы (или минимум и максимум или что-то одно из этих экстремумом).

Решение. Найдём второй дифференциал функции Лагранжа:

В нашем случае, так как первое и третье составляющие равны нулю, нам не придётся подставлять в них значения множителя Лагранжа. Зато нужно найти отношения между дифференциалами dx и dy :

Теперь можем найти значение условного экстремума исходной функции, являющееся максимумом:

.

Это заданная исходной функцией максимальная площадь прямоугольника, который можно ограничить верёвкой, длина которой равна 100.

Пример 2. Найти условные экстремумы функции двух переменных при условии .

Шаг 1. Составим функцию Лагранжа:

.

Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y :

Подставим эти выражения в третье уравнение и найдём значения множителя Лагранжа:

Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции при двух значениях множителя Лагранжа:

Эти значения икса и игрека являются координатами двух стационарных точек. Таким образом, получили стационарные точки .

Шаг 3. Найдём частные производные второго порядка функции Лагранжа:

:

Найдём второй дифференциал функции Лагранжа по формуле

:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, меньшее нуля, следовательно, точка — точка условного максимума:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, большее нуля, следовательно, точка — точка условного минимума:

.

Таким образом, условные экстремумы заданной функции найдены.

Пример 3. Найти условные экстремумы функции двух переменных при условии .

Шаг 1. Составим функцию Лагранжа:

.

Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y :

Получаем, что , однако подстановка этих значений переменных в третье уравнение системы не даёт верного равенства. Поэтому считаем, что на самом деле второй сомножитель равенства равен нулю: . Отсюда получаем

Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что . Из третьего уравнения системы получаем:

Получили две стационарные точки:

Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что .

На основании вычислений двух первых стационарных точек получилаем ещё две стационарные точки:

Шаг 3. Найдём частные производные второго порядка функции Лагранжа:

:

Найдём второй дифференциал функции Лагранжа по формуле

:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, меньшее нуля, следовательно, точки — точки условного максимума:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, большее нуля, следовательно, точки — точки условного минимума:

.

Таким образом, условные экстремумы заданной функции найдены.

Аналогичным образом можно находить условные экстремумы функций трёх и более переменных.

Источник