что такое ускоренное движение

Ускорение. Равноускоренное движение

Что такое ускоренное движение

Ускоренное движение — что это такое? Хороший вопрос. Давайте разберем это понятие по словам.

«Движение» — значит, что-то двигается. Ага, значит тело перемещается, значит у него есть какая-то скорость.

«Ускоренное» — значит «убыстренное», с возрастающей скоростью, когда тело двигается все быстрее и быстрее. Ага, значит скорость не постоянная. Она меняется. Тело двигается все быстрее, быстрее и быстрее. То есть скорость все время увеличивается.

Чтобы быть конкретнее, посмотрим на пример: мальчик на велосипеде разгоняется из состояния покоя. Сначала у него скорость 5 5 5 км/ч, потом 1 0 10 1 0 км/ч, потом 1 5 15 1 5 км/ч, 2 0 20 2 0 км/ч, 2 5 25 2 5 км/ч, 3 0 30 3 0 км/ч и т.д. — насколько у него хватит сил.

Точно так же, как мальчик разгоняется на велосипеде, кто-то, например девочка на самокате, может тормозить, останавливаться, двигаться все медленнее, медленнее и медленнее. В конце — остановиться. Сначала у нее может быть скорость 1 0 10 1 0 км/ч, потом 5 5 5 км/ч, а потом 0 0 0 км/ч. То есть скорость все время уменьшается на 5 5 5 км/ч.

Вернемся к примеру с девочкой. Мы видим, что ее скорость начинает возрастать в отрицательном направлении. То есть наше замедленное движение девочки на самокате переходит в ускоренное движение (когда скорость набирается), но уже в противоположную сторону. Именно поэтому замедленное движение — это вариант ускоренного движения. Поэтому между ускоренным и замедленным движениями (как правило) не делают различий и называют их просто ускоренным движением.

В итоге мы пришли к тому, что ускоренное движение — это движение, при котором меняется скорость. Но мы помним, что скорость — это векторная величина. А любой вектор характеризуется двумя величинами: длиной и направлением. Так вот, оказывается, что тело движется с ускорением в случае, если меняется скорость по величине (тело убыстряет свое движение) или же тело меняет направление скорости (тело поворачивает). Первый случай (с изменением величины — или, как говорят, модуля) мы рассмотрим сейчас в теме «Равноускоренное движение», а второй случай — с поворотом — в теме «Движение по окружности», когда тело поворачивает, а значит — изменяет направление скорости.

Ускорение

— это очень полезная для нас формула. Ее нужно запомнить.

Источник

Ускорение при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v ₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Основы механики для чайников. Часть 1: Кинематика

В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Источник

Скорость. Ускорение. Равноускоренное прямолинейное движение

1. Реальное механическое движение — это движение с изменяющейся скоростью. Движение, скорость которого стечением времени изменяется, называют неравномерным движением.

При неравномерном движении координату тола уже нельзя определить но формуле ​ \( x=x_0+v_xt \) ​, так как значение скорости движения не является постоянным. Поэтому для характеристики быстроты изменения положения тела с течением времени при неравномерном движении вводят величину, называемую средней скоростью.

Средней скоростью ​ \( \vec_ <ср>\) ​ неравномерного движения называют физическую величину, равную отношению перемещении \( \vec \) тела ко времени ​ \( t \) ​, за которое оно произошло: ​ \( \vec_<ср>=\frac\) ​.

2. Важно, что, зная среднюю скорость неравномерного движения на каком-либо участке траектории, нельзя определить положение тела на этой траектории в любой момент времени. Например, если средняя скорость движения автомобиля за 2 часа 50 км/ч, то мы не можем сказать, где он находился через 0,5 часа от начала движения, через 1 час, 1,5 часа и т.п., поскольку он мог первые полчаса двигаться со скоростью 80 км/ч, затем какое-то время стоять, а какое-то время ехать в пробке со скоростью 20 км/ч.

3. Двигаясь по траектории, тело проходит последовательно все её точки. В каждой точке траектории оно находится в определённые моменты времени и имеет какую-то скорость.

Мгновенной скоростью называют скорость тела в данный момент времени в данной точке траектории.

При дальнейшем уменьшении перемещения и соответственно времени движения тела они станут такими маленькими, что прибор, например спидометр, перестанет фиксировать изменение скорости, и движение за этот малый промежуток времени можно считать равномерным. Средняя скорость на этом участке и есть мгновенная скорость тела в т.О.

4. Одним из видов неравномерного движения является равноускоренное движение. Равноускоренным движением называют движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение.

Слова «любые равные промежутки времени» означают, что какие бы равные промежутки времени (2 с, 1 с, доли секунды и т.п.) мы ни взяли, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.

5. Характеристикой равноускоренного движения, помимо скорости и перемещения, является ускорение.

Ускорение тела при равноускоренном движении — векторная физическая величина, равная отношению изменения скорости тела к промежутку времени, за который это изменение произошло.

Направление ускорения совпадает с направлением скорости движения, если модуль скорости увеличивается, ускорение направлено противоположно скорости движения, если модуль скорости уменьшается.

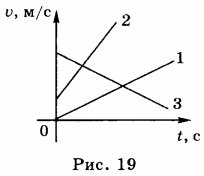
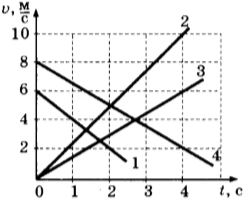
7. Как видно из формулы скорости равноускоренного движения, она линейно зависит от времени. Графиком зависимости модуля скорости от времени является прямая, составляющая некоторый угол с осью абсцисс (осью времени). На рисунке 19 приведены графики зависимости модуля скорости от времени.

График 1 соответствует движению без начальной скорости с ускорением, направленным так же, как и скорость; график 2 — движению с начальной скоростью \( v_ <02>\) и с ускорением, направленным так же, как и скорость; график 3 — движению с начальной скоростью \( v_ <03>\) и с ускорением, направленным в сторону, противоположную направлению скорости.

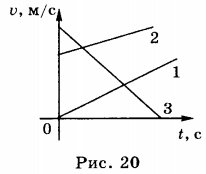
8. На рисунке приведены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).

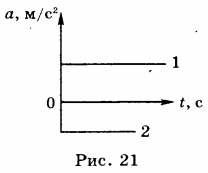
9. На рисунке 21 приведены графики зависимости проекции ускорения равноускоренного движения от времени.

График 1 соответствует движению, проекция ускорения которого положительна, график 2 — движению, проекция ускорения которого отрицательна.

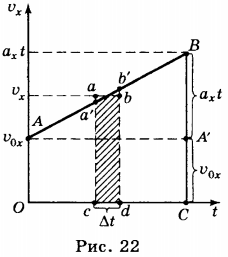
10. Формулу перемещения тела при равноускоренном движении можно получить, используя график зависимости проекции скорости этого движения от времени (рис. 22).

Выделим на графике малый участок ​ \( ab \) ​ и опустим перпендикуляры из точек​ \( a \) ​ и ​ \( b \) ​ на ось абсцисс. Если промежуток времени ​ \( \Delta\) ​, соответствующий участку ​ \( cd \) ​ на оси абсцисс мал, то можно считать, что скорость в течение этого промежутка времени не изменяется и тело движется равномерно. В этом случае фигура ​ \( cabd \) ​ мало отличается от прямоугольника и её площадь численно равна проекции перемещения тела за время, соответствующее отрезку ​ \( cd \) ​.

На такие полоски можно разбить всю фигуру ОАВС, и её площадь равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время ​ \( t \) ​ численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: ​ \( S_x= \frac<1><2>(OA+BC)OC \) ​.

Полученная формула позволяет определить положение (координату) тела в любой момент времени, если известны начальная скорость, начальная координата и ускорение.

Если начальная скорость тела равна нулю, то: ​ \( v^2_x=2a_xs_x \) ​.

Полученная формула позволяет рассчитать тормозной путь транспортных средств, т.е. путь, который проезжает, например, автомобиль до полной остановки. При некотором ускорении движения, которое зависит от массы автомобиля и силы тяги двигателя, тормозной путь тем больше, чем больше начальная скорость автомобиля.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

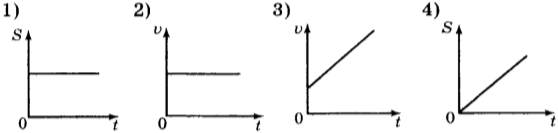
1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?

2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?

1) 200 м/с 2
2) 20 м/с 2
3) 2 м/с 2
4) 0,5 м/с 2

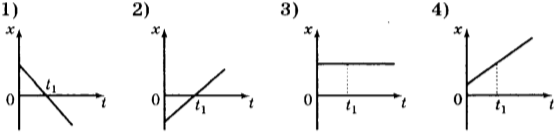
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси ​ \( Оx \) ​. У какого из тел в момент времени ​ \( t_1 \) ​ скорость движения равна нулю?

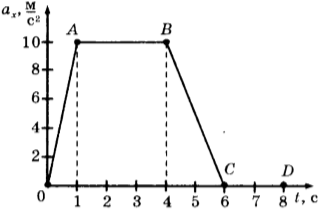
4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси ​ \( Оx \) ​.

Равноускоренному движению соответствует участок

1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD

5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.

Чему равен путь, пройденный телом за третью секунду?

1) 4 м
2) 4,5 м
3) 5 м
4) 9 м

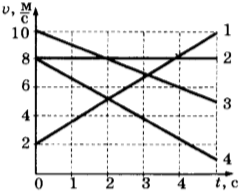
6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.

Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?

1) только 1
2) только 2
3) только 4
4) 3 и 4

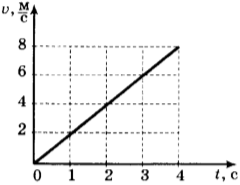
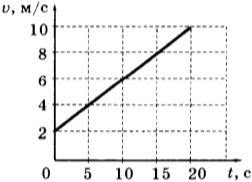
7. Используя график зависимости скорости движения тела от времени, определите его ускорение.

8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?

1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с

10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.

1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с

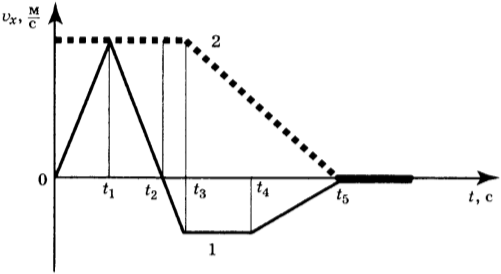
11. Два тела движутся по оси ​ \( Оx \) ​. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени ​ \( t_3-t_5 \) ​ тело 2 движется равноускоренно.
2) К моменту времени ​ \( t_2 \) ​ от начала движения тела прошли одинаковые пути.
3) В промежутке времени ​ \( 0-t_3 \) ​ тело 2 находится в покое.
4) В момент времени ​ \( t_5 \) ​ тело 1 останавливается.
5) В промежутке времени ​ \( t_3-t_4 \) ​ ускорение ​ \( a_x \) ​ тела 1 отрицательно.

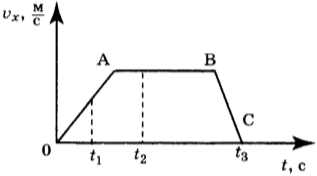
12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени ​ \( t_1 \) ​ тело имело максимальное по модулю ускорение.
4) Момент времени ​ \( t_3 \) ​ соответствует остановке тела.
5) В момент времени ​ \( t_2 \) ​ тело имело максимальное по модулю ускорение.

Часть 2

13. Зависимость координаты от времени для некоторого тела описывается уравнением ​ \( x=12t-t^2 \) ​. В какой момент времени скорость движения равна нулю?

Источник