что такое упорядоченные пары
Упорядоченные пары. Декартово (прямое) произведение множеств. Отношения
В предыдущем разделе операции над множествами давали множества той же природы. Например, если исходные множества были множествами чисел, то и полученные в результате операций множества были множествами чисел. В этом разделе мы определим операцию, с помощью которой меняется природа элементов получающихся множеств.
Определение 2.1. Упорядоченной парой (набор из 2 объектов) из элементов a и b (a,b), взятых именно в этом порядке, называется множество, состоящее из двух множеств, включающих элемент a: <a>,<a,b>.
Таким образом, понятие упорядоченной пары не выводит рассмотрение за пределы теории множеств. Но тем не менее независимое определение упорядоченной пары технически удобнее. Исходя из приведенного определения, доказывается справедливость следующей леммы:
Лемма: упорядоченные пары (a,b) и (c,d) равны тогда и только тогда, когда выполняется условие: (a,b) = (c,d) | a = с & b = d
Обобщением понятия упорядоченной пары является упорядоченный n-набор или картеж. В отличии от конечного множества
Определение 2.2. Множество всех картежей длины n на множествах А1, … Аn называется декартовым.
Пусть А и В – два множества.
Определение 2.3. Прямым (декартовым) произведением двух множеств А и В называется множество упорядоченных пар, в котором первый элемент каждой пары принадлежит множеству А, а второй множеству В.
Степенью множества А называется его прямое произведение самого на себя.
Теорема:|А´В| = |А| ´ |В|
Таким образом, всего имеется |А|·|В| упорядоченных пар.
Пусть А и В – два множества.
Определение 2.4. Бинарным отношением R из множества А в множество В называется подмножество прямого произведения: R Ì A ´ B.
Для бинарных отношений обычно используется инфиксная форма записи:
Упорядоченная пара
Пара в математике может быть определена с различных точек зрения.
Содержание
Определение пары в формальной математике
Пусть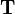 
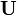
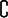
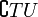
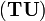
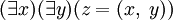
и 
— термы и 
— субстантивный знак веса 2, тогда знакосочетание 
также является термом и обозначается 
. Подробнее: соотношение 
обозначают словами « z есть пара».
Имеет место так называемая аксиома пары.
Аксиома пары
Определение пары в теории множеств
Непустое множество A называется множеством из двух элементов или парой: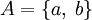 
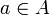
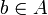
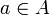
, если после вычитания из него множества, состоящего только из одного элемента 
, останется множество, которое состоит также из одного элемента 
(при этом определение не зависит от выбора и порядка следования указанного элемента ).
Упорядоченная пара
Наибольшее приложение имеют упорядоченные пары.
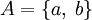
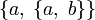
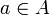
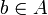
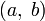
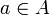
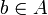
Если задана пара , то пара 
называется упорядоченной парой элементов и и обозначается 
. При этом элемент называется первым элементом пары, а элемент — вторым элементом пары.
Литература
Полезное
Смотреть что такое «Упорядоченная пара» в других словарях:
упорядоченная пара — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN ordered pair … Справочник технического переводчика
Пара (математика) — У этого термина существуют и другие значения, см. Пара. Пара в математике может быть определена с различных точек зрения. Содержание 1 Определение пары в формальной математике 1.1 Акс … Википедия
Пара — В Викисловаре есть статья «Пара» Омонимы, не связанные с числом 2, см. в Пара (значения). Пара имя существительное, обознач … Википедия
БИВЕКТОР — упорядоченная пара векторов аффинного пространства отложенных от общего начала. Б. полагается равным нулю, если составляющие его векторы коллинеарны. Ненулевой Б. определяет в Анесущую его двумерную плоскость. Два Б. наз. параллельными, если… … Математическая энциклопедия
ДУБЛЕТ — упорядоченная пара гиперплоскостей n мерного аффинного пространства. Задание Д. равносильно заданию ковариантного вектора. В центроаффинной геометрии Д. определяется единственной гиперплоскостью краем Д. М. И. Войцехоеский … Математическая энциклопедия
Граф (математика) — У этого термина существуют и другие значения, см. Граф (значения). Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность непустого множества вершин и множества пар… … Википедия
Граф (теория графов) — Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи как дуги, или рёбра. Для… … Википедия
Двудольный ориентированный граф — Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи как дуги, или рёбра. Для… … Википедия
Неориентированный граф — с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи как дуги, или рёбра. Для разных областей… … Википедия
Орграф — Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи как дуги, или рёбра. Для… … Википедия
Заказанные пары также называются 2-кортежи, или же последовательности (иногда списки в контексте информатики) длины 2. Упорядоченные пары скаляры иногда называют двумерными векторов. (Технически это злоупотребление обозначениями, поскольку упорядоченная пара не обязательно должна быть элементом векторное пространство.) Записи упорядоченной пары могут быть другими упорядоченными парами, что позволяет рекурсивное определение упорядоченного п— пары (упорядоченные списки п объекты). Например, упорядоченная тройка (а,б,c) можно определить как (а, (б,c)), т.е.как одна пара вложена в другую.
В заказанной паре (а, б), предмет а называется первая запись, а объект б то вторая запись пары. Как вариант, объекты называют первым и вторым. составные части, первый и второй координаты, или влево и вправо прогнозы заказанной пары.
Декартовы произведения и бинарные отношения (и поэтому функции) определены в терминах упорядоченных пар.
Содержание
Общие
В набор всех упорядоченных пар, первая запись которых находится в некотором наборе А и чья вторая запись находится в некотором наборе B называется Декартово произведение из А и B, и написано А × B. А бинарное отношение между сетами А и B это подмножество из А × B.
Неформальные и формальные определения
В некоторых вводных учебниках математики дается неформальное (или интуитивно понятное) определение упорядоченной пары, например
Обычно за этим следует сравнение с набором из двух элементов; указывая, что в наборе а и б должны быть разными, но в упорядоченной паре они могут быть равны, и хотя порядок перечисления элементов набора не имеет значения, в упорядоченной паре изменение порядка отдельных записей изменяет упорядоченную пару.
Это «определение» неудовлетворительно, потому что оно носит только описательный характер и основано на интуитивном понимании порядок. Однако, как иногда отмечают, использование этого описания не причинит вреда, и почти каждый думает об упорядоченных парах таким образом. [4]
Определение упорядоченной пары с помощью теории множеств
Если согласиться, что теория множеств привлекательный основа математики, то все математические объекты должны быть определены как наборы какой-то. Следовательно, если упорядоченная пара не считается примитивной, она должна быть определена как набор. [5] Ниже приводится несколько теоретико-множественных определений упорядоченной пары.
Определение Винера
Норберт Винер предложил первое теоретическое определение упорядоченной пары в 1914 году: [6]
Он заметил, что это определение позволило определить типы из Principia Mathematica ресурсы. Principia Mathematica взял типы, и, следовательно, связи всех арностей, как примитивный.
Винер использовал <<б>> вместо <б>, чтобы сделать определение совместимым с теория типов где все элементы в классе должны быть одного «типа». С б вложенный в дополнительный набор, его тип равен < < а >, ∅ > 
с.
Определение Хаусдорфа
Примерно в то же время, что и Винер (1914), Феликс Хаусдорф предложил свое определение:
Определение Куратовского
В 1921 г. Казимеж Куратовски предложил ныне принятое определение [8] [9] заказанной пары (а, б):
Обратите внимание, что это определение используется, даже если первая и вторая координаты идентичны:
Учитывая некоторую упорядоченную пару п, недвижимость «Икс первая координата п«можно сформулировать как:
Недвижимость «Икс вторая координата п«можно сформулировать как:
Вот как мы можем извлечь первую координату пары (используя обозначение для произвольное пересечение и произвольный союз):
Вот как можно извлечь вторую координату:
Варианты
Доказательство того, что определения удовлетворяют характеристическому свойству
Предполагать <CD> = <а>. потом с = d = а, и так <<c>, <CD>> = <<а>, <а, а>> = <<а>, <а>> = <<а>>. Но потом <<а>, <а, б>> также будет равно <<а>>, так что б = а что противоречит а ≠ б. Предполагать <c> = <а, б>. потом а = б = с, что также противоречит а ≠ б. Следовательно <c> = <а>, так что с = а и <CD> = <а, б>. Если d = а были правдой, то <CD> = <а, а> = <а> ≠ <а, б>; противоречие. Таким образом d = b это так, так что а = с и б = г.
Если. Если (а, б)обеспечить регресс = (CD)обеспечить регресс,(б, а)K = (Округ Колумбия)K. Следовательно, б = г и а = с.
Только если. Если а = с и б = г, тогда <<б>, <а, б>> = <<d>, <CD>>.Таким образом (а, б)обеспечить регресс = (CD)обеспечить регресс.
Только если: Предполагать <а, <а, б>> = <c, <CD>>.Потом а находится в левой части и, следовательно, в правой части. Поскольку равные множества имеют равные элементы, один из а = с или же а = <CD> должно быть так.
Если а = <CD>, то по аналогичным рассуждениям, указанным выше, <а, б> находится в правой части, поэтому <а, б> = c или же <а, б> = <CD>. Если <а, б> = c тогда c в <CD> = а и а в c, и эта комбинация противоречит аксиоме регулярности, так как <а, в> не имеет минимального элемента в отношении «element of.» Если <а, б> = <CD>, тогда а является элементом а, из а = <CD> = <а, б>, что снова противоречит закономерности. Следовательно а = с должен держать.
Снова мы видим, что <а, б> = c или же <а, б> = <CD>.
Опция <а, б> = c и а = с подразумевает, что c является элементом c, что противоречит закономерности. Итак, у нас есть а = с и <а, б> = <CD>, и так: <б> = <а, б> <а> = <CD> <c> = <d>, так б = d.
Определение Куайна – Россера
Россер (1953) [13] использовал определение упорядоченной пары из-за Куайн что требует предварительного определения натуральные числа. Позволять N быть набором натуральных чисел и определить сначала
Наконец, определите упорядоченную пару (А, B) как несвязное объединение
В теория типов и в ее продуктах, таких как аксиоматическая теория множеств NFпара Куайна – Россера имеет тот же тип, что и ее проекции, и поэтому называется упорядоченной парой «уровня типа». Следовательно, это определение имеет то преимущество, что позволяет функция, определенный как набор упорядоченных пар, чтобы иметь тип только на 1 выше, чем тип его аргументов. Это определение работает, только если набор натуральных чисел бесконечен. Так обстоит дело в NF, но не в теория типов или в НФУ. Дж. Баркли Россер показали, что существование такой упорядоченной пары на уровне типов (или даже упорядоченной пары «повышение типов на 1») влечет аксиома бесконечности. Подробное обсуждение упорядоченной пары в контексте теории множеств Квиниана см. В Holmes (1998). [15]
Определение Кантора – Фреге
В начале развития теории множеств, до того, как были обнаружены парадоксы, Кантор вслед за Фреге определил упорядоченную пару из двух множеств как класс всех отношений, которые выполняются между этими множествами, предполагая, что понятие отношения является примитивным: [16]
Это определение недопустимо в большинстве современных формализованных теорий множеств и методологически аналогично определению кардинал множества как класс всех множеств, равнодействующих данному множеству. [17]
Определение Морзе
Теория множеств Морса – Келли бесплатно использует правильные классы. [18] Морс определила упорядоченную пару так, чтобы ее проекции могли быть как собственными классами, так и наборами. (Определение Куратовского не допускает этого.) Сначала он определил упорядоченные пары, проекции которых являются множествами в манере Куратовского. Затем он переопределенный пара
Это отображает возможные пары, проекции которых являются собственными классами. Приведенное выше определение Куайна – Россера также допускает правильные классы как прогнозы. Точно так же тройка определяется как тройка следующим образом:
Теория категорий
Теоретико-категориальный товар А × B в категория наборов представляет собой набор упорядоченных пар, причем первый элемент происходит из А и второй исходящий от B. В этом контексте указанное выше характерное свойство является следствием универсальная собственность продукта и того факта, что элементы набора Икс можно отождествить с морфизмами от 1 (одноэлементное множество) до Икс. Хотя разные объекты могут обладать универсальным свойством, все они естественно изоморфный.
Упорядоченная пара
Декартовы произведения и бинарные отношения (и, следовательно, функции ) определяются в терминах упорядоченных пар.
Содержание
Общие [ править ]
Неформальные и формальные определения [ править ]
В некоторых вводных учебниках математики дается неформальное (или интуитивно понятное) определение упорядоченной пары, например
Обычно за этим следует сравнение с набором из двух элементов; указывая на то, что в наборе a и b должны быть разными, но в упорядоченной паре они могут быть равными и что, хотя порядок перечисления элементов набора не имеет значения, в упорядоченной паре изменяется порядок отдельных записей. заказанная пара.
Определение упорядоченной пары с использованием теории множеств [ править ]
Определение Винера [ править ]
Норберт Винер предложил первое теоретико-множественное определение упорядоченной пары в 1914 году: [6]
Винер использовал << b >> вместо < b >, чтобы сделать определение совместимым с теорией типов, где все элементы в классе должны быть одного «типа». Если b вложен в дополнительный набор, его тип равен ‘s. < < a >, ∅ > <\displaystyle \<\
Определение Хаусдорфа [ править ]
Примерно в то же время, что и Винер (1914), Феликс Хаусдорф предложил свое определение:
Определение Куратовского [ править ]
Обратите внимание, что это определение используется, даже если первая и вторая координаты идентичны:
Для некоторой упорядоченной пары p свойство « x является первой координатой p » можно сформулировать как:
Вот как мы можем извлечь первую координату пары (используя обозначение для произвольного пересечения и произвольного объединения ):
Вот как можно извлечь вторую координату:
Варианты [ править ]
Доказательство того, что определения удовлетворяют характеристическому свойству [ править ]
Снова мы видим, что < a, b > = c или < a, b > = < c, d >.
Определение Куайна – Россера [ править ]
φ ( x ) := σ [ x ] = < σ ( α ) ∣ α ∈ x >= ( x ∖ N ) ∪ < n + 1 : n ∈ ( x ∩ N ) >. <\displaystyle \varphi (x):=\sigma [x]=\<\sigma (\alpha )\mid \alpha \in x\>=(x\smallsetminus \mathbb
ψ ( x ) := σ [ x ] ∪ < 0 >= φ ( x ) ∪ < 0 >. <\displaystyle \psi (x):=\sigma [x]\cup \<0\>=\varphi (x)\cup \<0\>.>
Определение Кантора – Фреге [ править ]
В начале развития теории множеств, до того, как были обнаружены парадоксы, Кантор вслед за Фреге определил упорядоченную пару из двух множеств как класс всех отношений, которые выполняются между этими множествами, предполагая, что понятие отношения примитивно: [16]
Это определение недопустимо в большинстве современных формализованных теорий множеств и методологически аналогично определению кардинала множества как класса всех множеств, равноправных с данным множеством. [17]
Определение Морзе [ править ]
Это отображает возможные пары, проекции которых являются собственными классами. Приведенное выше определение Куайна – Россера также допускает собственные классы в качестве проекций. Точно так же тройка определяется как тройка следующим образом:
Теория категорий [ править ]
Декартовы произведения и бинарные отношения (и, следовательно, функции ) определяются в терминах упорядоченных пар.
СОДЕРЖАНИЕ
Общие
Неформальные и формальные определения
В некоторых вводных учебниках математики дается неформальное (или интуитивно понятное) определение упорядоченной пары, например
Обычно за этим следует сравнение с набором из двух элементов; указывая, что в наборе a и b должны быть разными, но в упорядоченной паре они могут быть равными и что хотя порядок перечисления элементов набора не имеет значения, в упорядоченной паре изменяется порядок отдельных записей. заказанная пара.
Определение упорядоченной пары с помощью теории множеств
Определение Винера
Норберт Винер предложил первое теоретико-множественное определение упорядоченной пары в 1914 году:
Винер использовал << b >> вместо < b >, чтобы сделать определение совместимым с теорией типов, где все элементы в классе должны быть одного «типа». Если b вложен в дополнительный набор, его тип равен ‘s. < < а >, ∅ > <\ Displaystyle \ <\ <а \>, \ emptyset \>>
Определение Хаусдорфа
Примерно в то же время, что и Винер (1914), Феликс Хаусдорф предложил свое определение:
Определение Куратовского
Обратите внимание, что это определение используется, даже если первая и вторая координаты идентичны:
Для некоторой упорядоченной пары p свойство « x является первой координатой p » можно сформулировать как:
Вот как мы можем извлечь первую координату пары (используя обозначение для произвольного пересечения и произвольного объединения ):
Вот как можно извлечь вторую координату:
Варианты
Доказательство того, что определения удовлетворяют характеристическому свойству
Снова мы видим, что < a, b > = c или < a, b > = < c, d >.
Определение Куайна – Россера
Определение Кантора – Фреге
В начале развития теории множеств, до того, как были обнаружены парадоксы, Кантор вслед за Фреге определил упорядоченную пару из двух множеств как класс всех отношений, которые выполняются между этими множествами, предполагая, что понятие отношения примитивно:
Это определение недопустимо в большинстве современных формализованных теорий множеств и методологически аналогично определению кардинала множества как класса всех множеств, равнодоступных данному множеству.
Определение Морзе
Это отображает возможные пары, проекции которых являются собственными классами. Приведенное выше определение Куайна – Россера также допускает собственные классы в качестве проекций. Точно так же тройка определяется как тройка следующим образом:
Аксиоматическое определение
Определение помогает избежать так называемых случайных теорем типа (a, a) = <>, ∈ (a, b), если определение Куратовского (a, b) = <,
Теория категорий