что такое уникальные цифры в математике 5 класс
Что такое удивительные числа?
Числа пронизывают все сферы жизни человека. Еще великий Пифагор утверждал, что все вещи в мире можно представить в виде чисел. Посредством производящих счет величин человечеству удалось определить целый ряд вселенских законов и разгадать тайны в истории. Но даже среди них встречаются самые необычные. Что же такое удивительные числа и чем они отличаются от обычных величин?
Удивительные свойства простых чисел
Многие наверняка замечали, что порой приходится удивляться не сложному, а простому. Это же правило распространяется и на мир чисел.
Простыми числами принято считать натуральные величины, которые способны делиться только на самих себя и на единицу. Среди них встречаются удивительные числа-близнецы – пары, которые различаются на 2. К примеру: 5 и 7; 11 и 13; 17 и 19. На рубеже первой сотни насчитывается всего 8 таких пар. По мере дистанцирования от нулевой отметки количество пар сокращается. Примечательно, что близнецы могут образовывать сосредоточения, формируя «четверки», например: 11, 13, 17, 19. Сколько же таких скоплений можно сформировать пока неизвестно.
В математике существует такой термин как «проблема Гольдбаха». Суть ее в том, что еще в 1742 г. Гольдбах, бывший на тот момент членом Петербургской Академии наук, заметил, что любая целая величина натурального ряда, вышеследующая за пятеркой, являет собой сумму, включающую максимум три слагаемых из простых чисел. К примеру: 34=31+3, 52=48+4…
Ученый испытал множество величин. И каждая из них представляла собой сумму, включающую 2 или 3 слагаемых.
Российский математик Л.Эйлер пошел еще дальше, предположив, что любое четное число натурального ряда, вышеследующее за двойкой, являет собой сумму из слагаемых, представленных двумя простыми числами. Это: 28=11+17=23+5; или 12=5+7; 64=59+5=41+23=47+17.
Открытия о составных числах
Не меньше вопросов и споров возникает при изучении составных чисел – величин, имеющих более двух делителей.
Замечательные «смиты»
Так именуют подкатегорию составных чисел, сумма цифр которых в десятичной системе исчисления соответствует сумме цифр его простых сомножителей при условии учета кратности. Их существует бесконечно много, но все они компактно упакованы посредством степеней. Чаще всего их можно наблюдать среди фигурных: 22 – пятиугольное, 378 – треугольное, 121 – квадратное.
Наглядным примером может служить равенство 2х101=202, поскольку каждая из его сторон по обе стороны «=» соответствуют «4». Так 2+0+2=4, и 2+1+0+1= 4.
В семействе «смитов» встречается немало диковинок:
Настоящими «изюминками» этого семейства выступают десятизначные величины, при написании которых каждая цифра используется лишь единожды. К примеру: 9 876 542 103 и 1 023 465 798.
Цикличность величины 142857
Одним из самых удивительных чисел по праву можно считать 142857. Оно необычно тем, что при умножении каждой из первых шести величин натурального ряда на него в результате будет получаться цилиндрический сдвиг этого шестизначного числа. В ответе каждый раз будут присутствовать одни и те же цифры, только они будут смещаться, двигаясь по типу ленты.
Секрет такой удивительной периодичности кроется в том, что 142857 выступает периодом преобразования простой дроби 1/7 в десятичную. Поэтому значения, расположенные после знака «=» являются периодами дробей: 1/7, 2/7, 3/7…
Число Шахерезады
Не менее интересно и «число Шехеризады». Именно оно проходит лейтмотивом через сборник арабских сказок «Тысяча и одна ночь». Но удивительно оно по той причине, что наделено целым рядом уникальнейших свойств. Перечислим лишь основные среди них:
1001 – палиндром или перевертыш. Оно отличается симметрией записи и потому читается одинаково в обоих направлениях. К примеру:
Еще одно удивительное свойство 1001 – при умножении на него любой трехзначной величины в результате получается та же самая величина, только прописанная дважды. К примеру: 756х1001=756756. Зная эту закономерность, у любого желающего не составит труда умножать на 1001 любые трехзначные величины.
Золотое сечение
Что объединяет пальцы человеческой ладони и спирали улитки, древнеегипетские пирамиды и произведение «Мона Лиза»? Ответ кроется в удивительных числах, а точнее их последовательности, которые являются божественной мерой красоты.
Последовательность, именуемая как ряд Фибоначчи, уникальна тем, что каждое «звено цепи» образуется из суммы двух предыдущих. Вот как выглядит эта цепочка: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …
Составляющие ее величины имеют еще одну интересную особенность. Если разделить любую величину из «цепи» на предшествующую ей, в ответе всегда будет значение, максимально приближенное к иррациональному числу, десятичное представление которого всегда не периодично и бесконечно. Это 1.61803398875…
Это соответствие частей называется Золотое сечение. 1,6180339887 – величина, которая очерчивает совершенные универсальные пропорции в изобразительном искусстве и науке. Считается, что две величины находятся в Золотой пропорции, если их коэффициент к большей является точно таким же, как и соразмерность между большей и меньшей. Варианты таких соразмерностей:
Формообразующий закон симметрии с удивительной настойчивостью проявляется в объектах, несущую эстетическую ценность у разных народов и эпох. Исходя из общепринятой пропорции, свои расчеты сегодня производят ученые.
Дизайнеры и модельеры берут за основу мерки с фигуры человека, которая построена по закону Золотой пропорции. Вот лишь некоторые соотношения 1:1.618, которые неизменно прослеживаются в теле любого человека. На голове это расстояние:
Ведь многочисленные исследования подтверждают: если пропорции любых частей тела приближены к пропорции золотого сечения – получается идеальное телосложение, что выступает ключевым критерием красоты.
Математическая константа Пи
Самая популярная математическая константа выражает соотношение окружности к диаметру круга. Буквенное обозначение константы и образовано от первых букв греческих слов, обозначающих «периметр» и «окружность».
Главное свойство этого удивительного числа в том, что оно никогда не кончается и не повторяется. Первые 50 символов после знака препинания имеют такой вид:
Максимальное количество цифр Пи после запятой рассчитал посредством сверхмощного компьютера японский ученый в 2011 г. Их количество составляет 10 трлн. цифр. В процессе работы он вывел интересное статистическое наблюдение. В первом млн. знаков после запятой присутствует:
Пи применяют в областях, требующих максимальной вычислительной мощности: при составлении прогноза погода, в мировой социально-экономической статистике. Наглядным воплощением величины Пи является и пирамида Хеопса в Каире. Соотношение высоты постройки с периметром основания создает это Пи.
Распространенные числовые суеверия
Предубеждения, связанные с удивительными свойствами чисел – одни из самых распространенных и долгоживущих. У многих из нас есть свое любимое число, которое непременно приносит удачу. Все это отголоски представлений наших предков о мистической силе производящих счет величин.
Священное число 7
7 выступает основным положением любой религии в мире. 7 добродетелей у христиан, 7 райских врат в исламе, 7 сокровищ чакравартина в буддизме…
Божественное число символизирует гармонию и совершенство:
Но главная причина особого значения этой величины в жизни людей в том, что все живые существа живут по лунному циклу. Он состоит из 4 фаз, каждая из которых включает 7 дней.
Исследования демонстрируют, что 7 – эквивалент максимальной вместительности оперативной памяти мозга. Из 10 представленных предметов или произнесенных слов человек может восстановить в памяти толь ко 7. Для реализации творческого труда оптимальное количество участников дискуссионной группы также составляет 7. Если в переговорах участвует более чем 4 человек, то коллектив автоматически распадется на группы по интересам.
Число Зверя
666 – составное число Смита удивительно тем, что его можно записать в двух вариантах при возрастающем порядке, используя для этого 9 неповторяющихся цифр, и одним вариантом в убывающем:
К тому же эта величина выступает:
Но для большинства людей эта величина известна под названием как «число Зверя». В Библии «7» упоминается как чистота и полноценность. Это 7 дней сотворения, 7 смертных грехов, 7 таинств. Шестерка – наоборот, нечто неполное и несовершенное, подобно Божему врагу.
Троекратность в 666 оказывает усиливающий негативный эффект, делая его символом крайней степени несовершенства. Обладает ли разрушительной силой эта величина доподлинно неизвестно. Но с десятки сотен фактов связанные с его негативным воздействием в истории человечества все же наберется.
Чертова дюжина
С точки зрения математики 13 это:
Людей, испытывающих ужас перед чертовой дюжиной, называют трискаидекафобами. Чтобы их не нервировать, многие европейские дома пронумерованы, минуя эту цифру, а во многих зданиях после 12-го этажа сразу следует 14-й. Отсутствует эта цифра и в нумерации кают на морских суднах, 13-й ряд зачастую отсутствует в самолетах.
При кажущейся простоте мир полон загадок и тайн. Но разгадать их под силу только самым пытливым умам.
Цифры (математика, 5 класс) – виды и классы
Под цифрами в математике понимают упорядоченную систему символов для записи чисел. Это своего рода шифр, который объединяет математику всего мира. Именно поэтому необходимо так важно разбираться в этой теме.
Характеристики понятия
Раньше люди обозначали числа различными значками: одна вертикальная короткая линия изображала единицу, а две – двойку и так далее. Этот метод записи до сих пор можно увидеть в записи «римских цифр».
Однако для громоздких вычислений в математике римский метод записи неудобен. Поэтому в обиход вошли арабские цифры. Ими было удобно пользоваться для различных видов вычислений. При этом арабские цифры удобно использовать не только в математике, но и в программировании, что стало еще одной причиной повсеместного распространения именно этого вида записи.
На самом деле арабские цифры являются индийскими. Но арабские страны переняли множество культурных особенностей у Индии. К тому же, многие математические трактаты древности составлены именно арабами с применением индийской системы исчисления. Позже, во время перевода трудов по математике, переводчики не стали искать корни происхождения цифр и назвали их арабскими.
Рис. 1. Таблица соответствия римских и арабских цифр.
Значение
Существуют разные варианты записи чисел. В зависимости от количества первоначальных цифр. В привычной нам десятичной системе их 10: от 0 до 9. Существует двоичная система, которая используется всего две цифры: 0 и 1. Эта система распространена в программировании. Существует множество других систем, каждая из которых когда-то использовалась человечеством. Но наиболее удобной была признана десятеричная с использованием арабских цифр.
В 5 классе изучают однозначные и многозначные натуральные числа. Получается, что в первом случае берется только одна цифра, а во втором – несколько. Наименьшим однозначным простейшим числом является «1», а наибольшим – «9».
Цифры, входящие в состав многозначного числа занимают определенные позиции, которые относят к разрядам.
Рис. 2. Состав числа.
Если в числе отсутствует разряд, то вместо него будет записана цифра «0». К примеру, запись «90» означает, что здесь содержится 9 десятков и 0 единиц. При этом разряды перед значащей цифрой тоже есть, но их не пишут. То есть, можно было бы записать «090», просто это загромождает запись.
Формирование больших чисел
Легко запоминать и читать длинные числа поможет знание классов. К первому классу относят первые три разряда: единицы, десятки и сотни. Все вместе они называются единицами. Следующий класс это три разряда тысяч, затем три разряда сотен тысяч, потом миллионы и так далее.
Для удобства классификации используют небольшие пробелы. К примеру, число 23465787 записывают так: 23 465 787. Тут совокупность цифр 787 относят к первому классу, 465 – второму, 23 – третьему. Обычно название класса единиц не проговаривают, так же как не проговаривают и название нулевых разрядов.
Рис. 3. Разряды чисел.
Что мы узнали?
Из определения понятия «цифра», нам стало известно, что это специальный знак, который используется для обозначения чисел. В современной математике используются «арабские цифры». Этот способ записи оказался более удобным для счислений. Полученное многозначное число читают слева на право, называя число единиц каждого класса с последующим добавлением названия класса.
Числа, имеющие уникальные (или отличные) цифры
Учитывая диапазон, напечатайте все числа, имеющие уникальные цифры.
Примеры :
// реализация C ++ для поиска уникальной цифры
// числа в диапазоне
#include
using namespace std;
// Функция для печати уникальных цифр
// в диапазоне от l до r.
void printUnique( int l, int r)
// Начало обхода чисел
// Находим цифры и поддерживаем их хэш
// если цифра встречается более 1 раза
// num будет 0 только когда цикл выше
// не получает перерыв, что означает
// номер уникален, поэтому напечатайте его.
// Реализация Java для поиска уникальной цифры
// числа в диапазоне
// Метод для печати уникальных цифр
// в диапазоне от l до r.
static void printUnique( int l, int r)
// Начало обхода чисел
boolean visited[] = new boolean [ 10 ];
// Находим цифры и поддерживаем их хэш
// если цифра встречается более 1 раза
visited[num% 10 ] = true ;
// num будет 0 только когда цикл выше
// не получает перерыв, что означает
// номер уникален, поэтому напечатайте его.
public static void main(String args[])
# Реализация Python3
# найти уникальную цифру
# числа в диапазоне
# Функция для печати
# уникальные цифры
# в диапазоне от l до r.
for i in range (l, r + 1 ):
# поддерживать свой хэш
# если встречается цифра
if visited[num % 10 ] = = 1 :
visited[num % 10 ] = 1 ;
# num будет 0 только тогда, когда
# выше цикла не получается
# перерыв это означает
# номер уникален так
# Этот код
# предоставлено mits
// реализация C # для поиска уникальной цифры
// числа в диапазоне
// Метод для печати уникальных цифр
// в диапазоне от l до r.
static void printUnique( int l, int r)
// Начало обхода чисел
bool []visited = new bool [10];
// Находим цифры и ведем
// если цифра встречается больше
// чем 1 раз, то перерыв
visited[num % 10] = true ;
// num будет 0 только когда
// вышеприведенный цикл не получается
// перерыв, означающий число
// уникален, поэтому напечатайте его.
public static void Main()
// Этот код предоставлен Sam007.
// Реализация PHP для поиска уникальных
// цифры в диапазоне
// Функция для печати уникальной цифры
// числа в диапазоне от l до r.
// Начало обхода чисел
// поддерживать свой хеш
// если цифра встречается больше
// чем 1 раз, то перерыв
// num будет 0 только когда выше
// цикл не прерывается
// означает, что номер уникален
// так что распечатай.
// Этот код предоставлен aj_36
?>
Выход :
Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.
Цифры

Всего получено оценок: 449.
Всего получено оценок: 449.
Под цифрами в математике понимают упорядоченную систему символов для записи чисел. Это своего рода шифр, который объединяет математику всего мира. Именно поэтому необходимо так важно разбираться в этой теме.
Характеристики понятия
Раньше люди обозначали числа различными значками: одна вертикальная короткая линия изображала единицу, а две – двойку и так далее. Этот метод записи до сих пор можно увидеть в записи «римских цифр».
Однако для громоздких вычислений в математике римский метод записи неудобен. Поэтому в обиход вошли арабские цифры. Ими было удобно пользоваться для различных видов вычислений. При этом арабские цифры удобно использовать не только в математике, но и в программировании, что стало еще одной причиной повсеместного распространения именно этого вида записи.
Значение
Существуют разные варианты записи чисел. В зависимости от количества первоначальных цифр. В привычной нам десятичной системе их 10: от 0 до 9. Существует двоичная система, которая используется всего две цифры: 0 и 1. Эта система распространена в программировании. Существует множество других систем, каждая из которых когда-то использовалась человечеством. Но наиболее удобной была признана десятеричная с использованием арабских цифр.
В 5 классе изучают однозначные и многозначные натуральные числа. Получается, что в первом случае берется только одна цифра, а во втором – несколько. Наименьшим однозначным простейшим числом является «1», а наибольшим – «9».
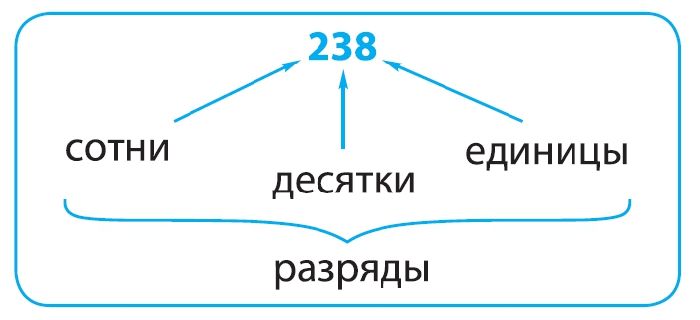
Если в числе отсутствует разряд, то вместо него будет записана цифра «0». К примеру, запись «90» означает, что здесь содержится 9 десятков и 0 единиц. При этом разряды перед значащей цифрой тоже есть, но их не пишут. То есть, можно было бы записать «090», просто это загромождает запись.
Формирование больших чисел
Легко запоминать и читать длинные числа поможет знание классов. К первому классу относят первые три разряда: единицы, десятки и сотни. Все вместе они называются единицами. Следующий класс это три разряда тысяч, затем три разряда сотен тысяч, потом миллионы и так далее.
Для удобства классификации используют небольшие пробелы. К примеру, число 23465787 записывают так: 23 465 787. Тут совокупность цифр 787 относят к первому классу, 465 – второму, 23 – третьему. Обычно название класса единиц не проговаривают, так же как не проговаривают и название нулевых разрядов.
Что мы узнали?
Из определения понятия «цифра», нам стало известно, что это специальный знак, который используется для обозначения чисел. В современной математике используются «арабские цифры». Этот способ записи оказался более удобным для счислений. Полученное многозначное число читают слева на право, называя число единиц каждого класса с последующим добавлением названия класса.
Классы и разряды
Видеоурок по этой теме можно посмотреть по ссылке: Разряды и классы. Десятичная система счисления.
Пройти тест по теме «Натуральные числа и действия над ними» можно по ссылке. Проверьте свои знания!
Мы выяснили, что в записи натурального числа значение, роль любой цифры зависит от места ее расположения в числе.
Разряд – это позиция, место расположения цифры в записи числа, начиная справа.
То есть, таблицу 2. в разделе чтение и запись натуральных чисел можно переписать следующим образом:
Таблица 1. Значение разрядов натуральных чисел.
Например, единицы 6-го разряда – это высший разряд по отношению к единицам 3-го разряда, и низшим разрядом по сравнению с единицами 9-го разряда.
Например, в числе 7777 четыре цифры 7, стоящих в разных разрядах, первом, втором, третьем и четвертом.
Если в натуральном числе нет ни одной единицы какого-либо разряда, тогда в этом разряде пишется цифра 0 (нуль).
В начале числа (слева) нули не ставятся.
Число 503 содержит 5 сотен, 0 десятков, 3 единицы.
Любые 10 единиц какого-нибудь разряда создают 1 единицу следующего за ним большего разряда. К примеру, 10 простых единиц создают 1 десяток, 10 сотен создают 1 тысячу.
И наоборот, любая единица высшего разряда включает в себя 10 единиц следующего за ней низшего разряда.
Из таблицы 1 можно заметить, что определенные части в наименовании значений, а именно: единицы, десятки, сотни, повторяются с различными дополнениями, такими как тысячи, миллионы, миллиарды. Например, единицы сотен и единицы миллиардов, сотни миллионов и сотни тысяч и пр.
Класс – это группа разрядов, содержащая в себе три разряда: единицы, десятки и сотни.
Классы, как и разряды, считают справа налево.
При записи многозначного числа можно оставлять небольшой пробел между разными классами, либо разделять их точками. Делается это для удобства чтения натуральных чисел.
Сколько содержится в числе единиц какого-нибудь разряда
Рассмотрим на примере. Допустим, необходимо определить, сколько всего десятков содержит в себе число 28924, то есть, сколько их содержится в десятках тысяч, в тысячах, в сотнях и в десятках данного числа вместе.
Итак, всего число в нашем примере содержит 2000 десятков, да еще 800 десятков, да еще 90 десятков, и еще 2 десятка, то есть, 2892 десятка.
Аналогичным образом можно узнать, что в числе из нашего примера содержится 289 сотен.
Для того, чтобы узнать, сколько всего единиц какого-нибудь разряда содержится в любом числе, необходимо мысленно убрать из него все единицы более низких разрядов, после чего прочитать то число, которое получилось.
Еще один пример: число 54.128.312 содержит: 5.412.831 десятков, 541.283 сотен, 54.128 тысяч, 5.412 десятков тысяч, 541 сотен тысяч, 54 миллиона, 5 десятков миллионов.



















