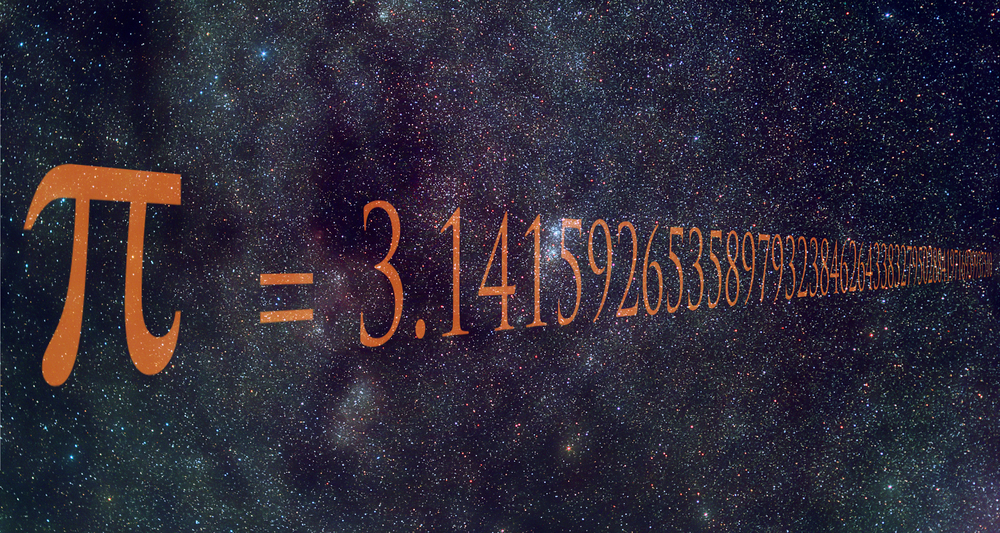что такое уникальное число
Что такое удивительные числа?
Числа пронизывают все сферы жизни человека. Еще великий Пифагор утверждал, что все вещи в мире можно представить в виде чисел. Посредством производящих счет величин человечеству удалось определить целый ряд вселенских законов и разгадать тайны в истории. Но даже среди них встречаются самые необычные. Что же такое удивительные числа и чем они отличаются от обычных величин?
Удивительные свойства простых чисел
Многие наверняка замечали, что порой приходится удивляться не сложному, а простому. Это же правило распространяется и на мир чисел.
Простыми числами принято считать натуральные величины, которые способны делиться только на самих себя и на единицу. Среди них встречаются удивительные числа-близнецы – пары, которые различаются на 2. К примеру: 5 и 7; 11 и 13; 17 и 19. На рубеже первой сотни насчитывается всего 8 таких пар. По мере дистанцирования от нулевой отметки количество пар сокращается. Примечательно, что близнецы могут образовывать сосредоточения, формируя «четверки», например: 11, 13, 17, 19. Сколько же таких скоплений можно сформировать пока неизвестно.
В математике существует такой термин как «проблема Гольдбаха». Суть ее в том, что еще в 1742 г. Гольдбах, бывший на тот момент членом Петербургской Академии наук, заметил, что любая целая величина натурального ряда, вышеследующая за пятеркой, являет собой сумму, включающую максимум три слагаемых из простых чисел. К примеру: 34=31+3, 52=48+4…
Ученый испытал множество величин. И каждая из них представляла собой сумму, включающую 2 или 3 слагаемых.
Российский математик Л.Эйлер пошел еще дальше, предположив, что любое четное число натурального ряда, вышеследующее за двойкой, являет собой сумму из слагаемых, представленных двумя простыми числами. Это: 28=11+17=23+5; или 12=5+7; 64=59+5=41+23=47+17.
Открытия о составных числах
Не меньше вопросов и споров возникает при изучении составных чисел – величин, имеющих более двух делителей.
Замечательные «смиты»
Так именуют подкатегорию составных чисел, сумма цифр которых в десятичной системе исчисления соответствует сумме цифр его простых сомножителей при условии учета кратности. Их существует бесконечно много, но все они компактно упакованы посредством степеней. Чаще всего их можно наблюдать среди фигурных: 22 – пятиугольное, 378 – треугольное, 121 – квадратное.
Наглядным примером может служить равенство 2х101=202, поскольку каждая из его сторон по обе стороны «=» соответствуют «4». Так 2+0+2=4, и 2+1+0+1= 4.
В семействе «смитов» встречается немало диковинок:
Настоящими «изюминками» этого семейства выступают десятизначные величины, при написании которых каждая цифра используется лишь единожды. К примеру: 9 876 542 103 и 1 023 465 798.
Цикличность величины 142857
Одним из самых удивительных чисел по праву можно считать 142857. Оно необычно тем, что при умножении каждой из первых шести величин натурального ряда на него в результате будет получаться цилиндрический сдвиг этого шестизначного числа. В ответе каждый раз будут присутствовать одни и те же цифры, только они будут смещаться, двигаясь по типу ленты.
Секрет такой удивительной периодичности кроется в том, что 142857 выступает периодом преобразования простой дроби 1/7 в десятичную. Поэтому значения, расположенные после знака «=» являются периодами дробей: 1/7, 2/7, 3/7…
Число Шахерезады
Не менее интересно и «число Шехеризады». Именно оно проходит лейтмотивом через сборник арабских сказок «Тысяча и одна ночь». Но удивительно оно по той причине, что наделено целым рядом уникальнейших свойств. Перечислим лишь основные среди них:
1001 – палиндром или перевертыш. Оно отличается симметрией записи и потому читается одинаково в обоих направлениях. К примеру:
Еще одно удивительное свойство 1001 – при умножении на него любой трехзначной величины в результате получается та же самая величина, только прописанная дважды. К примеру: 756х1001=756756. Зная эту закономерность, у любого желающего не составит труда умножать на 1001 любые трехзначные величины.
Золотое сечение
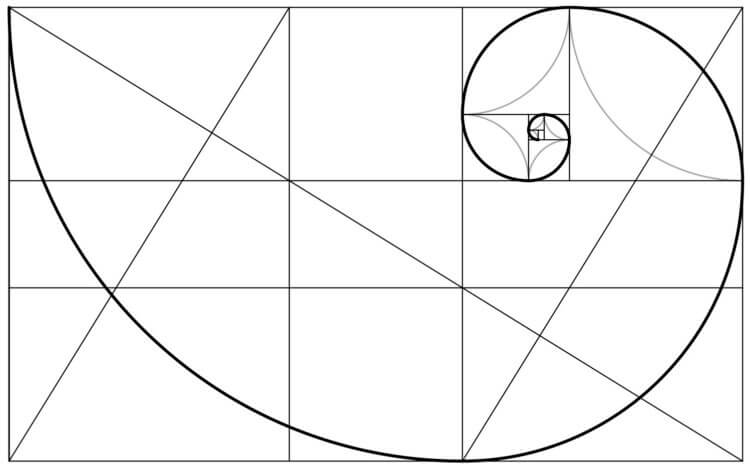
Что объединяет пальцы человеческой ладони и спирали улитки, древнеегипетские пирамиды и произведение «Мона Лиза»? Ответ кроется в удивительных числах, а точнее их последовательности, которые являются божественной мерой красоты.
Последовательность, именуемая как ряд Фибоначчи, уникальна тем, что каждое «звено цепи» образуется из суммы двух предыдущих. Вот как выглядит эта цепочка: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …
Составляющие ее величины имеют еще одну интересную особенность. Если разделить любую величину из «цепи» на предшествующую ей, в ответе всегда будет значение, максимально приближенное к иррациональному числу, десятичное представление которого всегда не периодично и бесконечно. Это 1.61803398875…
Это соответствие частей называется Золотое сечение. 1,6180339887 – величина, которая очерчивает совершенные универсальные пропорции в изобразительном искусстве и науке. Считается, что две величины находятся в Золотой пропорции, если их коэффициент к большей является точно таким же, как и соразмерность между большей и меньшей. Варианты таких соразмерностей:
Формообразующий закон симметрии с удивительной настойчивостью проявляется в объектах, несущую эстетическую ценность у разных народов и эпох. Исходя из общепринятой пропорции, свои расчеты сегодня производят ученые.
Дизайнеры и модельеры берут за основу мерки с фигуры человека, которая построена по закону Золотой пропорции. Вот лишь некоторые соотношения 1:1.618, которые неизменно прослеживаются в теле любого человека. На голове это расстояние:
Ведь многочисленные исследования подтверждают: если пропорции любых частей тела приближены к пропорции золотого сечения – получается идеальное телосложение, что выступает ключевым критерием красоты.
Математическая константа Пи
Самая популярная математическая константа выражает соотношение окружности к диаметру круга. Буквенное обозначение константы и образовано от первых букв греческих слов, обозначающих «периметр» и «окружность».
Главное свойство этого удивительного числа в том, что оно никогда не кончается и не повторяется. Первые 50 символов после знака препинания имеют такой вид:
Максимальное количество цифр Пи после запятой рассчитал посредством сверхмощного компьютера японский ученый в 2011 г. Их количество составляет 10 трлн. цифр. В процессе работы он вывел интересное статистическое наблюдение. В первом млн. знаков после запятой присутствует:
Пи применяют в областях, требующих максимальной вычислительной мощности: при составлении прогноза погода, в мировой социально-экономической статистике. Наглядным воплощением величины Пи является и пирамида Хеопса в Каире. Соотношение высоты постройки с периметром основания создает это Пи.
Распространенные числовые суеверия
Предубеждения, связанные с удивительными свойствами чисел – одни из самых распространенных и долгоживущих. У многих из нас есть свое любимое число, которое непременно приносит удачу. Все это отголоски представлений наших предков о мистической силе производящих счет величин.
Священное число 7
7 выступает основным положением любой религии в мире. 7 добродетелей у христиан, 7 райских врат в исламе, 7 сокровищ чакравартина в буддизме…
Божественное число символизирует гармонию и совершенство:
Но главная причина особого значения этой величины в жизни людей в том, что все живые существа живут по лунному циклу. Он состоит из 4 фаз, каждая из которых включает 7 дней.
Исследования демонстрируют, что 7 – эквивалент максимальной вместительности оперативной памяти мозга. Из 10 представленных предметов или произнесенных слов человек может восстановить в памяти толь ко 7. Для реализации творческого труда оптимальное количество участников дискуссионной группы также составляет 7. Если в переговорах участвует более чем 4 человек, то коллектив автоматически распадется на группы по интересам.
Число Зверя
666 – составное число Смита удивительно тем, что его можно записать в двух вариантах при возрастающем порядке, используя для этого 9 неповторяющихся цифр, и одним вариантом в убывающем:
К тому же эта величина выступает:
Но для большинства людей эта величина известна под названием как «число Зверя». В Библии «7» упоминается как чистота и полноценность. Это 7 дней сотворения, 7 смертных грехов, 7 таинств. Шестерка – наоборот, нечто неполное и несовершенное, подобно Божему врагу.
Троекратность в 666 оказывает усиливающий негативный эффект, делая его символом крайней степени несовершенства. Обладает ли разрушительной силой эта величина доподлинно неизвестно. Но с десятки сотен фактов связанные с его негативным воздействием в истории человечества все же наберется.
Чертова дюжина
С точки зрения математики 13 это:
Людей, испытывающих ужас перед чертовой дюжиной, называют трискаидекафобами. Чтобы их не нервировать, многие европейские дома пронумерованы, минуя эту цифру, а во многих зданиях после 12-го этажа сразу следует 14-й. Отсутствует эта цифра и в нумерации кают на морских суднах, 13-й ряд зачастую отсутствует в самолетах.
При кажущейся простоте мир полон загадок и тайн. Но разгадать их под силу только самым пытливым умам.
★ Уникальное простое
В теории чисел, уникальное простое число-это определенный вид простых чисел. чисел p ≠ 2, 5 называется уникальным, если нет других простых q, таких, что длина периода разложения в десятичную дробь, обратную, 1 / p (1) срок 1 / q (1). уникальный простой был впервые описан Сэмюэл Йетс в 1980.
Можно показать, что простой p является уникальным для периода n, если и только если там существует положительное целое число c, такие, что
где Φ n x это n первый круговой многочлен. В настоящее время насчитывается более пятидесяти уникальных простых или, может, простой. но ты знаешь только двадцать три уникальных простых, меньших 10 100. в таблице ниже показано 23 уникальный простой, меньше 10 100 последовательность A040017 для OEIS (ОЭИС) и их последовательность периодов A051627 для OEIS: (ОЭИС)
Простое число с периодом 294 звучит как число, обратное 7 0.142857142857142857.
Не показано в таблице, двадцать четвертый уникальное простое число содержит 128 признаки и продолжительность периода 320. он может быть записан как 9 32 0 32 2 1, где индекс n означает n последовательных копий цифру или группу цифр, которые представлены в индексе.
Хотя уникальные простые числа редких, он основывается на изучении простых, однозначных, и, возможно, простой гипотезы бесконечное количество уникальных простых любой простой repunit уникальная.
В 1996 году крупнейшими доказанными уникальный простой было 10 1132 1 / 10001, или используя выше запись, 99990000 141 1. Его период равен 2264 запись. с тех пор был несколько раз улучшен. К 2010 году крупнейшими доказанными уникальное простое число было 10.081 символов.
Три самые известные математические константы: как они появились и зачем нужны
В основе нашей Вселенной стоят числа, также известные как фундаментальные константы. Они показывают, как движутся галактики, как расширяется Вселенная, как вообще работает пространство и время. Рассказываем, кто их открыл и за что отвечает каждое число.
Читайте «Хайтек» в
Что такое математическая константа?
В противоположность переменным величинам существуют математические постоянные. Математическая постоянная, или константа — это величина, значение которой неизменно. Главной отличительной чертой математических констант является их независимость от физических измерений. Все математические константы имеют буквенный символ.
Число Пи
Число Пи (π) — это математическая константа, равная отношению длины окружности к ее диаметру. Десятичное представление числа никогда не заканчивается и является эталоном для высокопроизводительных вычислений.
Чему равно: 3,1415926535…
На сегодняшний день число Пи рассчитали с точностью до 62,8 трлн знаков после запятой — с помощью 32-ядерных процессоров AMD.
Если измерить веревкой длину окружности, получится, что она равна приблизительно трем ее диаметрам. Человечество выяснило это еще в древности. Кстати, это соотношение подходит для любой окружности — неважно, речь о часах или колесе обозрения. Иными словами, все окружности в мире связаны этой математической константой. Еще до нашей эры люди знали, что это число чуть больше трех. Вопрос в том, насколько. Столетия эта загадка не давала покоя мыслителям, поскольку имела большое значение и была почти высчитана. Но это «почти» растянулось на несколько тысяч лет.
Точное авторство числа Пи неизвестно. Вообще, открытие приписывается древним индийцам, грекам, китайцам и прочим хорошим людям. Впервые обозначил его греческой буквой π в начале XVIII века английский математик Уильям Джонс.
Числу π столько же лет, сколько всей математике: около 4 тыс. Старейшие шумерские таблички приводят для него цифру 25/8, или 3,125. Ошибка — меньше процента. Вавилоняне абстрактной математикой особо не увлекались, так что π вывели опытным путем, просто измеряя длину окружностей. Кстати, это первый эксперимент по численному моделированию мира.
Число Бога
Число Фи (φ) — число Бога, Золотое Сечение, Золотая Пропорция — у него много названий. Сам по себе это отношение одной части чего-либо к другой с коэффициентом 1,618 (это 61,8%), или 62% на 38%.
Чему равно: 1,6180339887…
Классическое определение Золотой Пропорции: меньшее относится к большему так, как большее относится к целому, с коэффициентом 1,618.
Принято считать, что впервые закономерности соотношения размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 году немецкий исследователь Цейзинг в своем научном труде «Эстетические исследования». За основу своей теории он взял учение о Золотом Сечении.
Еще в VI веке до н. э. древнегреческий философ и математик Пифагор ввел в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.
История Золотого Сечения связана еще с одним известным итальянским математиком Фибоначчи. До наших времен дошел ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д., известный как ряд Фибоначчи.
Особенность последовательности данных чисел заключается в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению Золотого Сечения (21:34=0,617, а 34:55=0,618). Впоследствии все исследователи Золотого Сечения в растительном и животном мире, искусстве и анатомии приходили к этому ряду как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибоначчи вывел, подсчитывая количество рожденных кроликов от пары кроликов за год.
Число Непера
Число е — своего рода двойник π. Если π отвечает за пространство, то е — за время, и тоже проявляет себя почти всюду. Скажем, радиоактивность полония-210 уменьшается в е раз за средний срок жизни одного атома, а раковина моллюска Nautilus — это график степеней е, обернутый вокруг оси.
Чему равно: 2,718281828…
е — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Приблизительно равно 2,71828. Иногда его называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».
Иными словами, число е является базовым соотношением роста для всех непрерывно растущих процессов. Оно участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов и других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е — это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Число открыл Джон Непер, шотландский математик, в 1618 году. Самого числа он не упоминал, зато выстроил на его основе свои таблицы логарифмов. Одновременно кандидатами в авторы константы считаются Якоб Бернулли, Лейбниц, Гюйгенс и Эйлер. Достоверно известно только то, что символ е взялся из фамилии последнего.
Как и π, е — трансцендентное число. Говоря проще, его нельзя выразить через дроби и корни. Есть гипотеза, что у таких чисел в бесконечном «хвосте» после запятой встречаются все комбинации цифр, какие только возможны.
Алгоритм генерации уникальных чисел
Есть число N, необходимо найти все уникальные числа до 0 до N. Например из чисел 123,132,213,231,312,321 уникальным будет только любое одно, но если N = 321, то скорее всего уникальным будет 123 т.к. в переборе встретиться первым. Простой перебор не подходит, т.к. для long значений он становится очень долгим.
2 ответа 2
Частичное решение вашей задачи.
Определение уникального числа:
Уникальным считается то число, которое имеет комбинацию цифр отличную от всех чисел проверенных ранее.
Пример 2. Уникальные трёхзначные числа от 100 до 199:
Решение:
Предлагаю не проверять все числа на уникальность перебором, а изначально конструировать только уникальные комбинации цифр. Для простоты возьмём числа без нулей (нули требуют дополнительной обработки):
Итак, возьмём девять начал состоящих из 1 цифры:
Обратите внимание, что первая цифра у нас зафиксирована, а вторую мы будем менять, создавая таким образом все возможны двухзначные комбинации.
4) Если нужно собрать трёхзначные комбинации, то берём всё возможные двухзначные комбинации полученные на предыдущем этапе, фиксируем их в виде строки и повторяем все шаги, начиная с пункт 1. Делать это удобно с помощью рекурсии.
Реализация на Python:
Output (сокращённый):
Другой вариант решения:
Число Фибоначчи. Почему оно так популярно в природе?
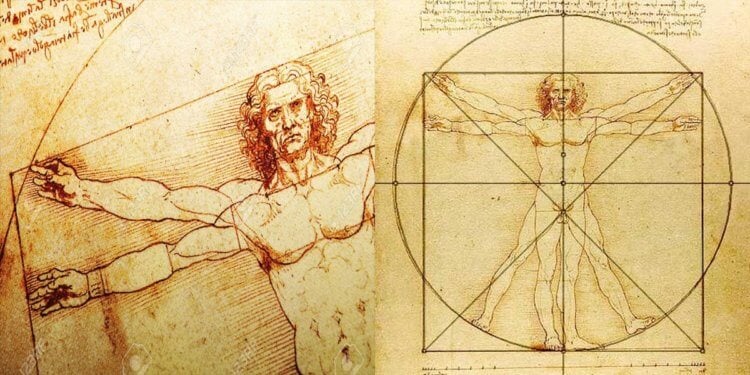
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.
«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи
Кто такой Фибоначчи?
Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.
В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.
Последовательность Фибоначчи
Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.
Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.
Леонардо Пизанский — тот самый создатель числа Фибоначчи
Где используется число Фибоначчи
Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.
Проявление золотого сечения в природе
Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!
Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.
Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.
Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением
Что такое золотое сечение
С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.
Так выглядит «золотое сечение»
Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.
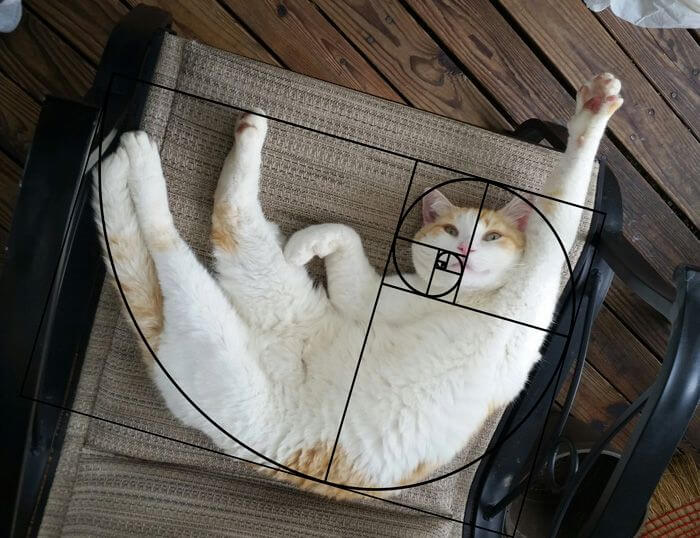
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты
Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.
Новости, статьи и анонсы публикаций
Свободное общение и обсуждение материалов
В 2016 году американские ученые выяснили, что на нашей планете обитает триллион видов живых существ, которые населяют сушу, воду и воздух. Все они выглядят п…
Пока вы читаете эти строки, вероятнее всего, вы сидите и считаете себя неподвижным. Но мы-то знаем, что на космическом уровне мы постоянно движемся. Земля вр…
В статье 2003 года философ из Оксфордского университета Ник Бостром изложил вероятность того, что наша реальность – это компьютерная симуляция, придуманная в…