что такое угол поворота
Угол поворота, угол произвольной величины.
В тригонометрии важным понятием является угол поворота. Ниже мы последовательно будем давать представление о повороте, и вводить все сопутствующие понятия. Начнем с общего представления о повороте, скажем о полном обороте. Далее перейдем к понятию угла поворота и рассмотрим его основные характеристики, такие как направление и величина поворота. Наконец, дадим определение поворота фигуры вокруг точки. Всю теорию по тексту будем снабжать поясняющими примерами и графическими иллюстрациями.
Навигация по странице.
Что называют поворотом точки вокруг точки?
Сразу отметим, что наряду с фразой «поворот вокруг точки» будем также использовать словосочетания «поворот около точки» и «поворот относительно точки», что обозначает одно и то же.
Введем понятие поворота точки вокруг точки.
Сначала дадим определение центра поворота.
Точку, относительно которой осуществляется поворот, называют центром поворота.
Теперь скажем, что получается в результате поворота точки.
Считают, что точка O при повороте вокруг самой себя переходит в саму себя. То есть, в результате поворота вокруг центра поворота O точка O переходит в саму себя.
Полный оборот
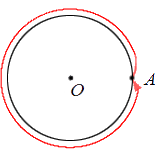
Дадим графическую иллюстрацию полного оборота.
Можно также говорить о частях полного оборота, например, о половине оборота, трети, четверти и т.д. оборота (при надобности смотрите статью доли и обыкновенные дроби).
Понятие угла поворота
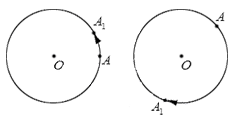
Одной из характеристик угла поворота является направление поворота. По направлению поворота судят о том, как осуществляется поворот точки – по часовой стрелке или против часовой стрелки.
Для обозначения углов поворота обычно используются строчные буквы греческого алфавита: 

Теперь поговорим о характеристиках угла поворота подробнее и по порядку.
Направление поворота
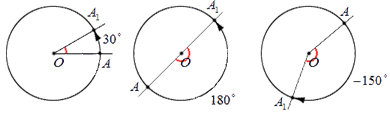
Условились считать поворотом в положительном направлении такой поворот, который осуществляется против хода часовой стрелки. Поворот по часовой стрелке называют поворотом в отрицательном направлении.
Проиллюстрируем повороты в положительном и отрицательном направлении. На чертеже ниже слева показан поворот в положительном направлении, а справа – в отрицательном.
Величина угла поворота, угол произвольной величины
Угол поворота точки, отличной от центра поворота, полностью определяется указанием его величины, с другой стороны, по величине угла поворота можно судить о том, как этот поворот был осуществлен.
Теперь осталось установить соответствие между величиной угла поворота и тем, какому повороту она соответствует.
Начнем с угла поворота, равного нулю градусам. Этому углу поворота отвечает перемещение точки А в себя. Другими словами, при повороте на 0 градусов вокруг точки O точка А остается на месте.
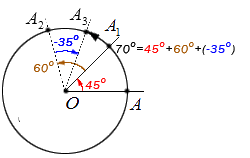
Углы поворота большие 180 градусов и меньшие −180 градусов определяются на основе следующего достаточно очевидного свойства последовательных поворотов: несколько последовательных поворотов точки A вокруг центра O равносильны одному повороту, величина которого равна сумме величин этих поворотов.
Поворот фигуры вокруг точки на угол
Понятие поворота точки легко расширяется на поворот любой фигуры вокруг точки на угол (речь идет о таком повороте, что и точка, относительно которой осуществляется поворот, и фигура, которую поворачивают, лежат в одной плоскости).
Под поворотом фигуры будем понимать поворот всех точек фигуры вокруг заданной точки на данный угол.
Угол поворота, угол произвольной величины
Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.
Поворот точки вокруг точки
Центр поворота – точка, относительно которой осуществлен поворот.
Полный оборот
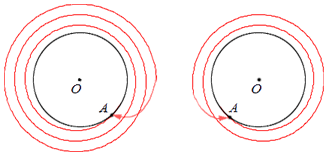
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:
В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.
Угол поворота
Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.
Разберем характеристики угла поворота подробнее.
Направление поворота
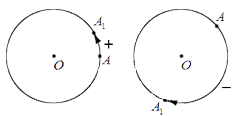
Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.
Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.
Величина угла поворота, угол произвольной величины
Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.
Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.
Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.
Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:
Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.
Поворот фигуры вокруг точки на угол
Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).
Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.
угол поворота
3.5 угол поворота (steering angle): Общий угол полного отклонения, измеряемый между передними и задними колесами при их перемещении относительно одной или более вертикальной оси из положения обычного прямолинейного движения в положение поворота.
1 Угол поворота для многоосных машин определяют между колесами первого переднего и последнего заднего мостов
2 Для рулевого управления с поворотными кулаками и трапецией характерно, что угол поворота колес, расположенных с внутренней стороны поворота, превышает угол поворота колес, расположенных с внешней стороны поворота, следовательно, при использовании такого рулевого управления должно быть также указано место измерения угла поворота.
Для определения угла поворота, полученного в случае комбинированного применения кинематических схем, включая систему управления с поворотными кулаками и трапецией, также необходимо указать место измерения угла поворота.
3.5 угол поворота (steering angle): Общий угол полного отклонения, измеряемый между передними и задними колесами при их перемещении относительно одной или более вертикальных осей из положения обычного прямолинейного движения в положение поворота.
1. Угол поворота для многоосных машин определяют между колесами первого переднего и последнего заднего мостов.
2. Для системы рулевого управления Аккерманн (с поворотными кулаками, рычагами и трапецией) характерно, что угол поворота колес, расположенных с внутренней стороны поворота, превышает угол поворота колес, расположенных с внешней стороны поворота. Следовательно, при использовании такого рулевого управления должно быть также указано место измерения угла поворота.
Для определения угла поворота, полученного в случае комбинированного применения кинематических схем, включая систему Аккерманн, также необходимо указать место измерения угла поворота.
4.14.1. Угол поворота для многоосных машин определяют между колесами первого переднего и последнего заднего мостов.
4.14.2. Для ручного управления с поворотными кулаками и трапецией характерно, что угол поворота колес, расположенных с внутренней стороны поворота, превышает угол поворота колес, расположенных с внешней стороны поворота. Следовательно, для этой системы должно быть также указано место измерения угла поворота.
4.14.3. Угол поворота, полученный в случае комбинированного применения кинематических схем, включая систему управления с поворотными кулаками и трапецией, определяют по п. 4.14, при этом должно быть указано место измерения в соответствии с требованиями п. 4.14.2.
2.4.3 угол поворота: Угол между проекцией продольной оси транспортного средства и линией пересечения плоскости колеса, которая представляет собой центральную плоскость шины, перпендикулярную к оси вращения колеса, и поверхности дороги.
6.19 угол поворота: Угловое перемещение запирающего или регулирующего элемента, исчисленное от закрытого положения затвора.
Величина углового перемещения запирающего или регулирующего элемента, исчисленная от закрытого положения затвора.
Смотри также родственные термины:
2.3.8 угол поворота ( e): Угол, указывающий расположение светоотражающего материала при помощи соответствующего обозначения с учетом поворота вокруг исходной оси.
6.20 угол поворота номинальный
Величина полного угла поворота без учета допусков.
6.22 угол поворота относительный
Отношение значения текущего угла поворота к номинальному углу поворота.
192 угол поворота рабочего оборудования a
Максимальный угол поворота рабочего оборудования от одного крайнего положения до другого
Угол поворота сварного шва b
Угол, который образует поперечная ось шва со своим нулевым положением (см. черт. 3).
6.21 угол поворота текущий
Угол поворота в промежутке от закрытого до полностью открытого положения затвора.
Полезное
Смотреть что такое «угол поворота» в других словарях:
угол поворота — твёрдого тела; угол поворота Угол между двумя последовательными положениями полуплоскости, неизменно связанной с телом и проходящей через его ось вращения … Политехнический терминологический толковый словарь
УГОЛ ПОВОРОТА — внешний угол между направлениями прямых участков жел. дор. пути при поворотах трассы. У. п. равен центральному углу, вершина к рого находится в центре круговой кривой, а стороны проходят через тангенсы. Технический железнодорожный словарь. М.:… … Технический железнодорожный словарь
угол поворота — Угловое перемещение запирающего или регулирующего элемента, исчисленное от закрытого положения затвора. [ГОСТ Р 52720 2007] Тематики арматура трубопроводная … Справочник технического переводчика
угол поворота ( e) — 2.3.8 угол поворота ( e): Угол, указывающий расположение светоотражающего материала при помощи соответствующего обозначения с учетом поворота вокруг исходной оси. Источник … Словарь-справочник терминов нормативно-технической документации
угол поворота — posūkio kampas statusas T sritis automatika atitikmenys: angl. angle of rotation; turning angle vok. Drehwinkel, m rus. угол поворота, m pranc. angle de rotation, m … Automatikos terminų žodynas
угол поворота — posūkio kampas statusas T sritis fizika atitikmenys: angl. turn angle; turning angle vok. Drehwinkel, m rus. угол поворота, m pranc. angle de rotation, m … Fizikos terminų žodynas
угол поворота — angle of rotation Угол, на который поворачивается любая линия, жестко связанная со звеном и перпендикулярная оси вращения. Шифр IFToMM: 2.2.28 Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
угол поворота растра — Угол, на который необходимо поворачивать проекционный или контактный растры, а также в издательских системах при растрировании изображений для разных красок (как цветных, так и черно белых оригиналов), чтобы при синтезе изображения на оттиске, с… … Справочник технического переводчика
угол поворота твердого тела — угол поворота Угол между двум и последовательными положениями полуплоскости, неизменно связанной с телом и проходящей через его ось вращения. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно… … Справочник технического переводчика
угол поворота растра — Угол, на который необходимо поворачивать проекционный или контактный растр, а также в издательских системах – при растрировании изображений для разных красок (как цветных, так и черно белых оригиналов), чтобы при синтезе изображения на оттиске с… … Краткий толковый словарь по полиграфии
Вращательное движение
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) ?,
скорость u — угловая скорость ?,
ускорение a — угловое ускорение ?
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
? — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
Соотношение между единицами угла
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ? от t). 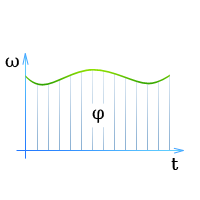
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость ? от t) и график углового ускорения (зависимость ? от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
? — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
? — угловая частота,
то
Период
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2?:
Угловая скорость
Из формулы для одного оборота следует:
Обратите внимание:
• формулы справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Равномерное движение тела по окружности
Говорят, что тело движется по окружности равномерно, если его угловая скорость постоянна, т.е. тело за равные промежутки времени поворачивается на один и тот же угол.
? — угловая скорость (постоянная в течение времени t)
? — угловое перемещение
t — время поворота на угол ?
Поскольку на графике угловой скорости площадь прямоугольника соответствует угловому перемещению, имеем:
Постоянная угловая скорость — есть отношение углового перемещения (угла поворота) ко времени, затраченному на это перемещение.
Единица СИ угловой скорости:
Равномерно ускоренное движение по окружности без начальной угловой скорости
Тело начинает двигаться из состояния покоя, и его угловая скорость равномерно возрастает.
? — мгновенная угловая скорость тела в момент времени t
? — угловое ускорение, постоянное в течение времени t
? — угловое перемещение тела за время t, (? в радианах)
t — время
Поскольку на графике скорости угловое перемещение равно площади треугольника, имеем:
Равномерно ускоренное движение по окружности с начальной угловой скоростью
Начальная скорость тела, равная ?0 в момент t = 0, изменяется равномерно на величину ??. (Угловое ускорение при этом постоянно.)
?0 — начальная угловая скорость
? — конечная угловая скорость
? — угловое перемещение тела за время t в радианах
t — время
? — угловое ускорение постоянное в течение времени t
Поскольку на графике скорости угловое перемещение соответствует площади трапеции под кривой скорости, имеем:
Так как площадь трапеции равна сумме площадей образующих ее треугольника и прямоугольника, получаем:
Далее из графика скорости следует
Совместив формулы мы получим
После преобразования получаем выражение, не содержащее времени:
Неравномерно ускоренное движение тела по окружности
Движение тела по окружности будет неравномерно ускоренным, если изменение угловой скорости происходит не пропорционально времени, т. е. если угловое ускорение не остается постоянным. В этом случае и угловая скорость и угловое ускорение являются функциями времени.
Связь величин ?, ? и ? представлена на соответствующих графиках.
Мгновенная угловая скорость
Полный угол поворота тела в любой момент времени можно определить по графику углового перемещения. Чем круче график, тем больше в данный момент времени мгновенная угловая скорость.
? — угол между касательной и осью времени t
? — мгновенная угловая скорость
? — угловое перемещение к моменту времени t

Мгновенной угловой скоростью называется первая производная функции ? = ?(t) по времени.
Обратите внимание:
1) чтобы вычислить мгновенную угловую скорость ?, необходимо знать зависимость углового перемещения от времени.
2) формула углового перемещения при равномерном движении тела по окружности и формула углового перемещения при равномерно ускоренном движении по окружности без начальной угловой скорости являются частными случаями формулы (2) соответственно для ? = 0 и ? = const.
Проинтегрировав обе части выражения, получим
Угловое перемещение есть интеграл по времени от угловой скорости.
Средняя угловая скорость
Средняя угловая скорость для некоторого интервала времени
Среднее число оборотов определяется аналогично формуле:
Вращательное движение тела, формулы
При вращательном движении твердого тела все элементы его массы, не лежащие на оси вращения, совершают движение по окружности. Аналогично и материальная точка, находящаяся на расстоянии r > 0 от оси вращения, также совершает движение по окружности, как и любое тело, достаточно удаленное от оси вращения.
Линейное перемещение Sл, линейная скорость uл и линейное ускорение aл при таком движении связаны между собой обычными для поступательного движения соотношениями.

Кроме того, эти величины связаны определенным образом с угловым перемещением ?, угловой скоростью ? и угловым ускорением ?.
| Sл | перемещение тела по траектории, | метр |
|---|---|---|
| Uл | скорость тела при движении по траектории, | метр / секунда |
| aл | ускорение данного тела при движении по траектории, | метр / секунда2 |
| r | радиус траектории, | метр |
| d | диаметр траектории, | метр |
| ? | угловое перемещение тела, | радиан |
| ? | угловая скорость тела, | радиан / секунда |
| ? | угловое ускорение тела, | радиан / секунда2 |
| f | частота, | Герц |
Примечание:Формулы справедливы для постоянных, мгновенных и средних величин, во всех случаях движения тела по окружности.
Векторные величины, характеризующие вращательное движение тела
| Угловая скорость и угловое ускорение тела являются векторными величинами. Эти векторы направлены вдоль оси вращения (аксиальные векторы), а их длина определяет величину соответствующих характеристик вращательного движения. Направление векторов определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения буравчика, рукоятка которого движется в том же направлении, что и тело. |  |
Определение:Если тело участвует одновременно в нескольких вращательных движениях, то результирующая угловая скорость определяется по правилу векторного (геометрического) сложения:
Величина результирующей угловой скорости определяется по аналогии с формулой (Сложение движений):
или, если оси вращения перпендикулярны друг другу
Примечание: Результирующее угловое ускорение определяется аналогичным образом. Графически результирующую можно найти как диагональ параллелограмма скоростей или ускорений.