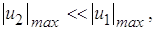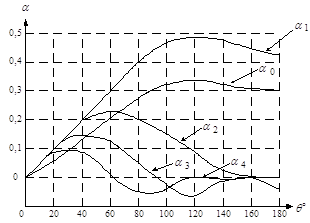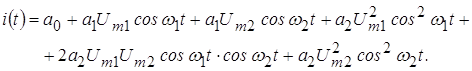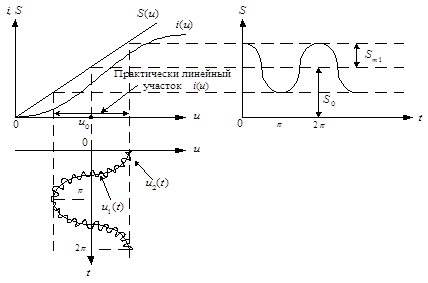что такое угол отсечки

Понятие угла отсечки. Коэффициенты Берга

В усилителях мощности одним из основных параметров является коэффициент полезного действия — к.п.д. В рассмотренном в предыдущей статье усилителе класса A через усилительный каскад постоянно протекает ток. В мощных усилителях он достигает значительной величины. Первоначально для увеличения экономичности усилителей вводили автоматическую регулировку положения рабочей точки в зависимости от уровня сигнала. Затем заметили, что в ряде случаев усиление возможно при ограничении сигнала снизу (отсечке).

После этого была выполнена исследовательская работа зависимости параметров синусоидального сигнала от угла отсечки. Понятие угла отсечки сигнала проще всего пояснить по рисунку 1.

Рисунок 1. Определение угла отсечки по выходному току

На данном рисунке часть синусоиды, показанная серым цветом, на выходе транзистора отсутствует (отсекается). Угол отсечки определяется как половина фазового угла прохождения тока через транзистор или электронную лампу за период синусоидального колебания. Так как ток на выходе усилительного прибора уже не соответствует входному сигналу, то при поступлении на вход синусоидального сигнала, на его выходе образуется ряд гармонических составляющих. Их можно определить при помощи преобразования Фурье:

(1),
(2),
(3),
(4),

Функции зависимости амплитуды гармоники от угла отсечки получили название функций Берга. По этим графикам можно определить уровень гармоники в выходном сигнале и коэффициент полезного действия. Функции Берга для первых пяти гармоник приведены на рисунке 2.

Рисунок 2. Графики коэффициентов Берга

На данных графиках угол отсечки, равный 180°, соответствует усилителю класса A. Для этого усилителя гармоники входного сигнала отсутствуют, а уровень тока потребления α0 и полезного сигнала α1 совпадают. Это соответствует коэффициенту полезного действия 50%. Угол отсечки, равный 120°, соответствует усилителю класса AB. В данном случае максимальный к.п.д можно ожидать в районе 65%, уровень второй гармоники — 18%, уровень третьей гармоники — 6%. Причем третья гармоника находится в противофазе с полезным сигналом.

Следует отметить, что коэффициент усиления тоже зависит от угла отсечки выходного тока. При уменьшении Θ он уменьшается. Это следует учитывать при проектировании усилителя мощности. График зависимости коэффициента усиления от угла отсечки приведен на рисунке 3

Рисунок 3. График зависимости коэффициента усиления по мощности от угла отсечки

Максимальная достижимая выходная мощность на выходе транзистора или электронной лампы тоже зависит от угла отсечки. График этой зависимости приведен на рисунке 4.

Рисунок 4. График зависимости выходной мощности от угла отсечки

Дата последнего обновления файла 5.04.2018

Понравился материал? Поделись с друзьями!

Вместе со статьей «Понятие угла отсечки. Коэффициенты Берга» читают:

Источник

Угол отсечки

Общее определение: Угол отсечки (Θ, рад) — угол, соответствующий изменению тока от максимального значения до нуля.

Частное определение: Угол отсечки (Θ, рад) — половина фазового угла, в течение которого диод в диодном выпрямителе открыт, то есть через него протекает ненулевой ток.

Экспериментально угол отсечки можно получить, измеряя ток, протекающий через диод.

(<<<2>>>)

где ω — круговая частота входного напряжения,
Δt — время, в течение которого диод открыт.

См. также

Полезное

Смотреть что такое «Угол отсечки» в других словарях:

угол отсечки — Часть периода гармонического сигнала, подводимого к активному элементу, уменьшенная в два раза и выраженная в угловых единицах, в течение которой через этот элемент протекает электрический ток. Примечание Рассматриваемый угол отсечки относится к… … Справочник технического переводчика

Угол отсечки — 16. Угол отсечки Часть периода гармонического сигнала, подводимого к активному элементу, уменьшенная в два раза и выраженная в угловых единицах, в течение которой через этот элемент протекает электрический ток. Примечание. Рассматриваемый угол… … Словарь-справочник терминов нормативно-технической документации

угол отсечки — atkirtos kampas statusas T sritis fizika atitikmenys: angl. angle of current flow; cutoff angle vok. Stromflußwinkel, m rus. угол отсечки, m pranc. angle de coupure, m … Fizikos terminų žodynas

Угол отсечки — 1. Часть периода гармонического сигнала, подводимого к активному элементу, уменьшенная в два раза и выраженная в угловых единицах, в течение которой через этот элемент протекает электрический ток Употребляется в документе: Приложение № 1 к ГОСТ… … Телекоммуникационный словарь

угол выключения [восстановления] запирающих свойств — угол отсечки — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы угол отсечки EN turnoff angle … Справочник технического переводчика

ОТСЕЧКИ УГОЛ — количеств. хар ка отсечки тока. О. у. равен т/2Т*360, где Т период синусоидального колебания, т время (в пределах одного периода) протекания тока. Выражается в градусах. Напр., если режим работы прибора (электронной лампы или транзистора) выбран… … Большой энциклопедический политехнический словарь

маска (угла отсечки спутника) — Один из параметров условий наблюдений спутника, входящий в миссию, характеризующий минимальный угол места спутников, входящих в данную программу измерений, ниже которого спутники не наблюдаются. [РТМ 68 14 01] Тематики спутниковая технология… … Справочник технического переводчика

ГОСТ 24375-80: Радиосвязь. Термины и определения — Терминология ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа: 304. Абсолютная нестабильность частоты радиопередатчика Нестабильность частоты передатчика Определения термина из разных документов: Абсолютная нестабильность… … Словарь-справочник терминов нормативно-технической документации

Парораспределительный механизм — Вальсхарта (паровоз П36) … Википедия

Паровозы — Паровоз Привод паровая машина Период 1804 60 е годы XX века Скорость до 202 км/ч Область применения … Википедия

Источник

Спектральный анализ колебаний в нелинейных преобразователях: метод кратных дуг, метод трех и пяти ординат, Метод функций Бесселя

Общие сведения

При изучении процессов нелинейных преобразований в первую очередь приходится решать задачу нахождения спектра колебаний на выходе преобразователей. Данная задача формулируется следующим образом.

Имеется безынерционный нелинейный преобразователь, характеристика которого аппроксимируется зависимостью i = f(u). На вход этого преобразователя поступает так называемое полигармоническое колебание вида

В частном случае это может быть моногармоническое колебание вида
u(t) = Ucos(ωt + φ).

Необходимо определить спектр тока i на выходе преобразователя. Такая задача получила название «спектральный анализ». Для решения этой задачи можно использовать аппарат рассмотренных ранее рядов Фурье. Однако такой метод определения спектра отклика оказывается весьма трудоемким, поэтому на практике применяются специальные методы спектрального анализа, связанные с рассмотренными ранее методами аппроксимации характеристик нелинейных преобразователей. При этом наибольшее распространение получили:

Метод кратных дуг

Данный метод является основным при использовании полиномиальной аппроксимации. Его удобно применять при анализе нелинейных преобразований в процессе модуляции, демодуляции, преобразования и деления частоты.

Пусть вольт-амперная характеристика нелинейного резистивного элемента аппроксимирована многочленом n-й степени:

На вход преобразователя подается гармоническое колебание вида
u(t) = Ucos(ωt + φ).

Выполнив соответствующие подстановки, получим

Воспользуемся следующими известными формулами:

позволяющими степени косинусов (синусов) заменить тригонометрическими формулами кратных аргументов, отсюда и происходит название данного метода.

Предположим x = ωt + φ, тогда, выполнив очевидные подстановки, получим:

Здесь

При произвольном номере гармоники общее выражение для тока имеет вид

Спектр амплитуд тока на выходе нелинейного преобразователя при воздействии одного гармонического колебания показан на рис. 3.5, а.

Из сказанного можно сделать следующие выводы.

Ранее отмечалось, что нелинейные преобразования вызывают появление новых спектральных составляющих, которых не было на входе. Данный эффект проявляется наиболее ярко, если на вход преобразователя подается колебание, являющееся суммой нескольких гармоник с различными частотами.

Пусть на нелинейный резистивный элемент поступает так называемое бигармоническое колебание вида

Рис. 3.5. Амплитудные спектры тока на выходе нелинейною преобразователя при воздействии одного (а) и двух (б) гармонических колебаний

Для упрощения анализа рассмотрим случай, когда вольт-амперная характеристика описывается многочленом 2-й степени (т.е. слабо нелинейный режим):

Выполним соответствующие подстановки:

Из этого выражения видно, что в выходном колебании содержатся составляющие, которые имелись в спектре входного колебания, а также появились и новые гармоники. Иными словами, на выходе имеются постоянная составляющая и первые, вторые гармоники входных сигналов. Принципиально новым является появление двух комбинационных колебаний с частотами (Формула) и (Формула). Амплитуды этих колебаний, равные (Формула), в одинаковой степени зависят от амплитуд каждого из входных сигналов. Комбинационные колебания обращаются в нуль, если на входе устройства отсутствует любой из двух входных сигналов.

Спектр амплитуд тока для рассмотренного случая показан на рис. 3.5, б.

Метод трех и пяти ординат

Данный метод применяют, как правило, при графических расчетах для оценки нелинейных искажений, возникающих в модуляторах, усилителях и других устройствах. Его отличительной особенностью является то, что в нем не требуется осуществлять аппроксимацию вольт-амперной характеристики нелинейного элемента.

Метод формул трех ординат позволяет определить значения постоянной составляющей и амплитуды первых двух гармоник тока в следующем виде:

Пусть характеристика нелинейного преобразователя задана графически (рис. 3.6).

Выберем на графике три ординаты и потребуем, чтобы значения тока в этих точках совпадали с его действительными значениями. Иными словами, возьмем следующие точки:

Рис. 3.6. Определение значений гармоник тока посредством выбора ординат характеристики нелинейного преобразователя

Подставив выбранные значения в формулу для тока, получим систему из трех уравнений:

Решив эту систему уравнений относительно (Формула), получим:

Аналогично используют формулу пяти ординат для определения значений тока первых четырех гармоник. В этом случае точность расчетов будет выше. Однако в целом точность нахождения амплитуд гармоник с использованием данного метода невысока: ошибка растет с увеличением амплитуды подводимого напряжения.

Метод функций Бесселя

Данный метод применяется при анализе работы демодуляторов и преобразователей частоты в случае, когда вольт-амперная характеристика аппроксимируется экспоненциальной функцией.

Пусть имеется нелинейный преобразователь в виде полупроводникового диода, характеристика которого аппроксимирована выражением

На его вход подается напряжение
u(t) = E + Ucosωt.

Подставив это напряжение в аппроксимирующее выражение, получим

Это выражение можно представить в виде ряда Фурье, для чего необходимо найти коэффициенты разложения, использовав выражения из теории функций Бесселя:

— модифицированная функция Бесселя n-го порядка от аргумента х.

При этом x = αU, φ = ωt.

Тогда разложение в ряд Фурье будет иметь следующий вид:

Из этого разложения видно, что постоянная составляющая тока

амплитуда первой гармоники

амплитуда n-й гармоники

Расчеты по данным выражениям показывают, что с увеличением номера гармоники ее амплитуда уменьшается. При выполнении расчетов можно использовать подробные таблицы функций Бесселя, приведенные в специальных справочниках.

Метод угла отсечки

Метод угла отсечки применяют при кусочно-линейной аппроксимации вольт-амперных характеристик. Он весьма эффективен для расчетов умножителей частоты, усилителей и генераторов, собранных на полупроводниковых приборах и лампах.

Пусть имеется нелинейный преобразователь, вольт-амперная характеристика которого аппроксимирована соотношением

где S — крутизна характеристики; U0 — напряжение отсечки.

На рис. 3.7 эта характеристика представляет собой две прямые линии.

Рассмотрим воздействие напряжения
u = E + Ucosωt,
где Ε — напряжение смещения, которое определяет рабочую точку.

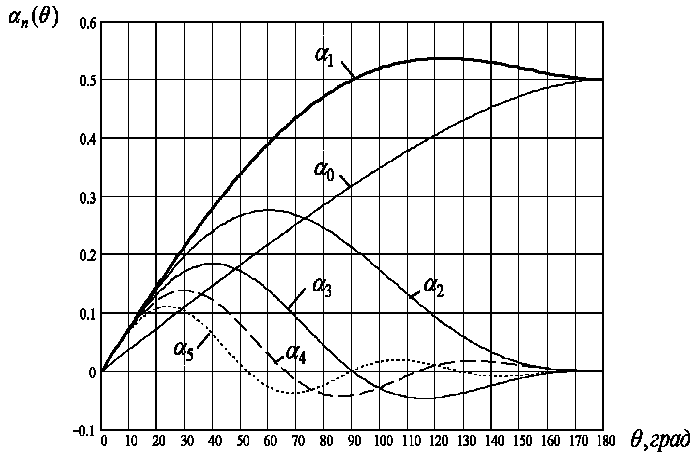
Из рис. 3.7 видно, что нелинейный элемент работает с отсечкой, т.е. часть входного напряжения, которая не заштрихована, не участвует в создании тока. Получаемые при этом импульсы тока характеризуются двумя величинами: высотой (Формула) и шириной, т. е. углом отсечки, который обозначен θ.

«Углом отсечки» называется часть периода колебания с частотой ω, в течение которого или ток изменяется от максимального значения до нуля, или входное напряжение изменяется от максимального U до U0. Угол отсечки θ = ωt и измеряется в градусах или в радианах. Следовательно, можно записать

откуда

Рис. 3.7. Пояснение процессов в нелинейном преобразователе при использовании для расчета метода угла отсечки

Определим значение выходного тока. Для чего подставим выражение входного напряжения u в соотношение, которым аппроксимирована вольт-амперная характеристика:

Поскольку при ωt = θ ток равен нулю (i = 0), можно записать

Вычитанием второго выражения из первого получим
i = SU(cosωt − cosθ).

При ωt = 0 выходной ток имеет максимальное значение

, т.е.

Полученная графическим построением периодическая последовательность импульсов тока является четной функцией, поэтому ее можно представить в виде ряда Фурье, в котором содержатся постоянная составляющая и косинусоидальные гармоники:

Постоянную составляющую найдем из соотношения

— коэффициент постоянной составляющей.

Соответственно амплитуда первой гармоники

Аналогично определяется амплитуда n-й гармоники:

n = 2, 3, 4, …

Иногда при расчете удобнее использовать нормированные коэффициенты гармоник (нормированные относительно значения максимального тока (Формула)):

Эти коэффициенты являются функциями только угла отсечки θ, поэтому для них имеются справочные графики и специальные таблицы, которые удобно применять в расчетах нелинейных преобразователей. Заметим, что для наиболее часто применяемого режима при θ = π/2

Анализ зависимостей позволяет сделать следующие выводы.

Источник

Анализ цепей методом угла отсечки

3. Анализ цепей методом угла отсечки

При работе нелинейной цепи с большими амплитудами входного сигнала, когда степенная аппроксимация не дает хороших результатов применяется кусочно-линейная аппроксимация. Работа НЭ происходит при этом с отсечкой выходного тока, и большое применение находит аналитический метод анализа, получивший название метода угла отсечки.

Форма тока в цепи, содержащей НЭ с характеристикой

(18)

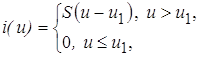
видна из графика, представленного на рисунке 7 (при условии, что на вход подано напряжение ).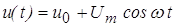

Рис. 7. График тока через НЭ при работе с отсечкой тока

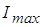
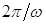
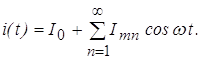
График тока имеет характерный вид периодической последовательности косинусоидальных импульсов, которые характеризуются амплитудой и длительностью 2, где – угол отсечки, числено равный половине той части периода, в течение которого через НЭ протекает ток. Период повторения импульсов равен . Спектральный состав такого периодического колебания легко определить, разложив функцию тока в ряд Фурье:

(19)

Угол отсечки легко найти из равенства :

(20)

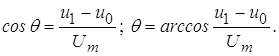
Функция тока определяется следующим выражением:

. (21)

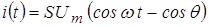
При :

. (22)

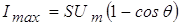
Амплитуды спектральных составляющих тока через НЭ определяются через коэффициенты Берга:

(23)

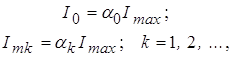
где коэффициенты являются функциями одного аргумента – угла отсечки , получили название коэффициентов (функций) Берга.

Рис. 8. Графики функций Берга

Таким образом, алгоритм вычисления амплитуд гармоник тока через НЭ может быть следующим:

1. По известным значениям , , определяется угол отсечки с помощью формулы (18).

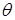
2. По формуле (20) или графически определяется величина .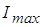

3. С помощью таблицы или по графикам (рис. 8) находят .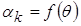

4. Вычисляются амплитуды гармоник: 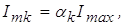k = 1, 2, ….

4. Воздействие двух гармонических сигналов на безынерционный НЭ

Для выявления основных закономерностей рассмотрим реакцию НЭ на воздействие двух гармонических сигналов. Такое воздействие принято называть бигармоническим:

(24)

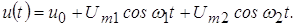
Для упрощения анализа на первом этапе воспользуемся аппроксимацией ВАХ нелинейного элемента полиномом второй степени:

(25)

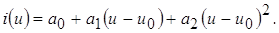
После подстановки (22) в (23) получим

Выполнив тригонометрические преобразования по формулам

и сгруппировав члены, получим следующее спектральное представление тока

(26)

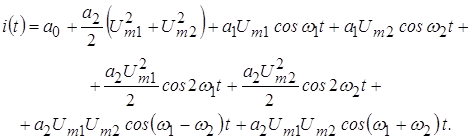
Анализ выражения (24) позволяет сделать вывод о значительном обогащении спектра тока по сравнению со спектром входного сигнала. В спектре выходного колебания, кроме слагаемых, имевшихся во входном сигнале – постоянной составляющей и гармоник на частотах ω₁ и ω₂, возникли гармонические составляющие суммарной и разностной частоты (ω₁ + ω₂) и (ω₁ – ω₂), а также компоненты с удвоенными частотами 2ω₁, 2ω₂.

При увеличении порядка аппроксимирующего полинома проблема вычисления амплитуд спектральных составляющих сводится к громоздким выкладкам, приводить которые в данной лекции нецелесообразно. В самом общем случае, когда ВАХ представлена полиномом n-й степени, спектр тока через НЭ (в случае бигармонического воздействия) будет включать составляющие с частотами

(27)

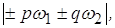
где p и q – целые числа, причем (p + q) ≤ n.

Сумма (p + q) называется порядком комбинационного колебания. Комбинационное колебание в общем случае можно записать

(28)

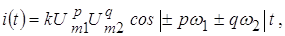
где k – коэффициент пропорциональности.

При построении различных радиотехнических устройств, являющихся элементами приемных и передающих трактов (модуляторы, детекторы, преобразователи частоты, дифференциальные усилители), приходится использовать нелинейные цепи с бигармоническим воздействием. При этом с помощью фильтрации выделяются нужные комбинационные составляющие (т. е. создающие полезный эффект в нагрузке в зависимости от реализуемой операции) и соответственно подавляются побочные продукты взаимодействия двух сигналов и . Теперь рассмотрим, как влияют амплитуды воздействующих сигналов и на соотношение амплитуд гармоник в спектре выходного тока.

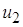
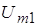
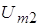
Параметрический режим работы нелинейного элемента

При реализации некоторых устройств аппаратуры связи, работа которых основана на использовании нелинейных электрических цепей (элементов) и бигармоническом воздействии, часто возникает практическая ситуация, когда амплитуда одного из напряжений значительно больше другого. Например, в преобразователе частоты супергетеродинного радиоприемного устройства амплитуда преобразуемого сигнала значительно меньше амплитуды напряжения местного источника гармонического напряжения (гетеродином). В этих условиях НЭ для сигнала с малой амплитудой выступает в качестве параметрического элемента. Графическая иллюстрация такого режима представлена на рисунке 9.

Рис. 9. Графическая иллюстрация параметрического режима работы

К нелинейному элементу с вольт-амперной характеристикой приложены два напряжения: гармонический сигнал с большой амплитудой и малое напряжение , в общем случае не обязательно гармоническое.

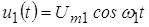
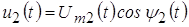
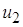
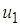
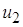
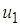
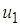
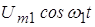
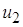
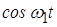
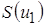
Учитывая малую величину напряжения по сравнению c , можно считать участок характеристики, на которой в данный момент времени действует напряжение , практически линейным (фрагмент ВАХ на рисунке 9). При этом напряжение действует как изменяющееся во времени напряжение смещения, т. е. источник перемещает рабочую точку на характеристике по закону . Таким образом, можно считать, что для малого колебания нелинейный элемент является линейным, но с изменяющейся по закону крутизной . Такой элемент и называется параметрическим, причем в роли переменного параметра выступает крутизна вольт-амперной характеристики.

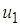
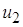
Выше уже говорилось о том, что очень важно обеспечить минимизацию побочных продуктов взаимодействия напряжений и , а также подчеркнуть, по возможности, полезную комбинационную составляющую. Рассмотрим условия, при которых может быть решена эта задача, для чего получим аналитическое выражение для тока через НЭ в общем виде.

Если на вход НЭ с характеристикой воздействуют два колебания: , причем выполняется неравенство

(29)

Источник