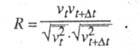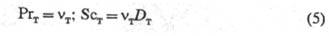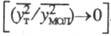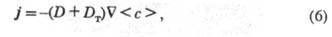что такое турбулентная диффузия
ТУРБУЛЕНТНАЯ ДИФФУЗИЯ
перенос в-ва в пространстве, обусловленный турбулентным движением среды. Под турбулентным понимают вихревое движение жидкости или газа, при к-ром элементы (частицы) среды совершают неупорядоченные, хаотич. движения по сложным траекториям, а скорость, т-ра, давление и плотность среды испытывают хаотич. флуктуации.
Если в турбулентном потоке в определенный момент времени множество элементов (частиц) расположено рядом один с другим, то в послед, моменты времени они рассеиваются по пространству так, что статистич. расстояние между любыми двумя произвольными частицами с течением времени возрастает. Проявления этого процесса во многом напоминают мол. диффузию.
В основе описания T. д. как процесса случайного блуждания частиц среды лежат выражения для среднеквадратичного смешения частиц 
где 

Поскольку T. д. и мол. диффузия независимы, общее смещение частицы будет определяться суммой:
Т. д. протекает по-разному в зависимости от масштаба турбулентности. Перенос в-ва при маломасштабной турбулентности описывают по аналогии с мол. диффузией. При крупномасштабной турбулентности среднее квадратичное смещение частиц с течением времени быстро увеличивается, причем этот рост обусловлен преим. крупными вихрями.
Предполагают, что турбулентный перенос в-ва в рассматриваемый момент времени в произвольной точке пространства определяется градиентом осредненной концентрации, взятым в той же точке пространства и в тот же момент времени (гипотеза Буссинеска). Так, плотность турбулентного потока массы в направлении к.-л. из осей координат, напр. *, выражают в виде:
Используя соотношения, аналогичные законам вязкости Ньютона и теплопроводности Фурье (см. Переноса процессы), вводят коэф. турбулентной кинематич. вязкости v т и турбулентной температуропроводности а т (м 2 /с). Последние в отличие от выраженных в тех же единицах измерения коэф. мол. диффузии D, температуропроводности аи кинематич. вязкости v не являются физ.-хим. характеристиками и зависят от параметров осредненного движения среды, а также от положения рассматриваемого элемента ее объема в потоке.
В общем случае выражение для плотности диффузионного потока в бинарной жидкой или газовой смеси с учетом мол. и турбулентного механизмов переноса записывают в виде:
Знание закономерностей Т. д. необходимо при описании хим.-технол. процессов, протекающих в потоках жидкости или газа, в т. ч. в дисперсных средах. T. д. оказывает влияние на структуру потоков в аппаратах и вносит свой вклад в продольное и поперечное перемешивание в-ва. Чаще всего продольное перемешивание снижает движущую силу массо-обменных процессов и ухудшает их показатели.
Лит.:Mонин А. С., Яглом А. Я., Статистическая гидромеханика, ч. 1-2, M., 1967; Берд Р., Стыоарт В., Л айтфут E., Явления переноса, пер. с англ., M., 1974; Рейнольде А. Дж., Турбулентные течения в инженерных приложениях, M., 1979. В. В. Дильман.
Однако было чрезвычайно сложно разработать конкретную и полностью функциональную модель, которую можно было бы применить к диффузии частиц во всех турбулентных системах из-за невозможности одновременно охарактеризовать как мгновенную, так и прогнозируемую скорость жидкости. В турбулентном потоке это является результатом нескольких характеристик, таких как непредсказуемость, быстрая диффузия, высокие уровни флуктуирующей завихренности и диссипация кинетической энергии.
СОДЕРЖАНИЕ
Приложения
Атмосферная диффузия и загрязнители
Атмосферная дисперсия, или диффузия, изучает, как загрязняющие вещества смешиваются в окружающей среде. В этот процесс моделирования включается множество факторов, таких как какой уровень атмосферы (-ов) происходит смешивание, стабильность окружающей среды и какой тип загрязнителя и источник смешиваются. Модели Эйлера и Лагранжа (обсуждаемые ниже) использовались для моделирования атмосферной диффузии и важны для правильного понимания того, как загрязнители реагируют и смешиваются в различных средах. Обе эти модели учитывают как вертикальный, так и горизонтальный ветер, но дополнительно интегрируют теорию диффузии Фика для учета турбулентности. Хотя эти методы должны использовать идеальные условия и делать многочисленные предположения, на данный момент трудно лучше рассчитать влияние турбулентной диффузии на загрязняющие вещества. Теория диффузии Фика и дальнейшие достижения в исследованиях атмосферной диффузии могут быть применены для моделирования эффектов, которые текущие уровни выбросов загрязняющих веществ из различных источников оказывают на атмосферу.
Турбулентное диффузионное пламя
Используя процессы плоской лазерно-индуцированной флуоресценции (PLIF) и измерения скорости изображения частиц (PIV), продолжаются исследования эффектов турбулентной диффузии в пламени. Основные области исследований включают системы сжигания в газовых горелках, используемых для выработки электроэнергии, и химические реакции в струйно-диффузионном пламени с участием метана (CH 4 ), водорода (H 2 ) и азота (N 2 ). Кроме того, двухимпульсная визуализация температуры Рэлея использовалась для корреляции мест угасания и возгорания с изменениями температуры и смешиванием химических веществ в пламени.
Моделирование
Эйлеров подход
Эйлеров подход к турбулентной диффузии фокусируется на бесконечно малом объеме в определенном пространстве и времени в фиксированной системе отсчета, в которой измеряются такие физические свойства, как масса, импульс и температура. Модель полезна, потому что статистику Эйлера можно последовательно измерить и она отлично подходит для химических реакций. Подобно молекулярным моделям, он должен удовлетворять тем же принципам, что и приведенное ниже уравнение неразрывности (где адвекция элемента или разновидностей уравновешивается его диффузией, генерацией в результате реакции и добавлением из других источников или точек) и уравнениям Навье-Стокса :
Если мы рассматриваем инертные частицы (без реакции) без источников и предполагаем, что молекулярная диффузия незначительна, выживают только члены адвекции в левой части уравнения. Решение этой модели сначала кажется тривиальным, однако мы проигнорировали случайную составляющую скорости плюс среднюю скорость в u j = ū + u j ‘, которая обычно связана с турбулентным поведением. В свою очередь, концентрационное решение для модели Эйлера также должно иметь случайную составляющую c j = c + c j ‘. Это приводит к проблеме замыкания бесконечных переменных и уравнений и делает невозможным решение для определенного c i при указанных предположениях.
К счастью, существует закрывающее приближение при введении концепции вихревой диффузии и ее статистических приближений для случайной концентрации и составляющих скорости от турбулентного перемешивания:
Подстановка в первое уравнение неразрывности и игнорирование реакций, источников и молекулярной диффузии приводит к следующему дифференциальному уравнению, учитывающему только приближение турбулентной диффузии в вихревой диффузии:
Лагранжев подход
Затем можно рассчитать концентрацию частиц в точке x и времени t, суммируя вероятности количества наблюдаемых частиц следующим образом:
Что затем оценивается путем возврата к интегралу pdf
Таким образом, этот подход используется для оценки положения и скорости частиц относительно их соседей и окружающей среды и аппроксимирует случайные концентрации и скорости, связанные с турбулентной диффузией, в статистике их движения.
Решения
Полученное решение для решения окончательных уравнений, перечисленных выше, для моделей Эйлера и Лагранжа для анализа статистики видов в турбулентном потоке, обе приводят к очень похожим выражениям для расчета средней концентрации в месте от непрерывного источника. Оба решения образуют гауссовский плюм и практически идентичны при предположении, что отклонения в направлениях x, y, z связаны с коэффициентом диффузии вихрей:
q = интенсивность выбросов видов, u = скорость ветра, σ i 2 = отклонение в i-м направлении.
При различных внешних условиях, таких как скорость направленного потока (ветер) и условия окружающей среды, измеряются отклонения и коэффициенты диффузии турбулентной диффузии, которые используются для расчета точной оценки концентраций в определенной точке от источника. Эта модель очень полезна в атмосферных науках, особенно при работе с концентрациями загрязняющих веществ в загрязнении воздуха, которые исходят из таких источников, как дымовые трубы, реки или автомобильные гусеницы на дороге.
Будущие исследования
Помимо этих усилий, до появления компьютеров были достигнуты успехи в полевых исследованиях. Теперь возможен мониторинг турбулентности, скорости и течений при перемешивании жидкостей в реальном времени. Это исследование оказалось важным для изучения циклов смешивания загрязняющих веществ в турбулентных потоках, особенно в системах питьевого водоснабжения.
Турбулентная диффузия
Однако было чрезвычайно сложно разработать конкретную и полностью функциональную модель, которую можно было бы применить к диффузии частиц во всех турбулентных системах из-за невозможности одновременно охарактеризовать как мгновенную, так и прогнозируемую скорость жидкости. В турбулентном потоке это является результатом нескольких характеристик, таких как непредсказуемость, быстрая диффузия, высокие уровни флуктуирующей завихренности и диссипация кинетической энергии. [2]
Содержание
Приложения [ править ]
Атмосферная диффузия и загрязнители [ править ]
Атмосферная дисперсия [3] или диффузия изучает, как загрязнители смешиваются в окружающей среде. В этот процесс моделирования включается множество факторов, таких как уровень атмосферы (-ов), в которой происходит перемешивание, стабильность окружающей среды и тип загрязняющего вещества и источника смешивания. Обе модели Эйлера и Лагранжа (обсуждаемые ниже) использовались для моделирования атмосферной диффузии и важны для правильного понимания того, как загрязнители реагируют и смешиваются в различных средах. Обе эти модели учитывают как вертикальный, так и горизонтальный ветер, но дополнительно интегрируют теорию диффузии Фика.для учета турбулентности. Хотя эти методы должны использовать идеальные условия и делать многочисленные допущения, на данный момент трудно лучше рассчитать влияние турбулентной диффузии на загрязнители. Теория диффузии Фика и дальнейшие достижения в исследованиях атмосферной диффузии могут быть применены для моделирования эффектов, которые текущие уровни выбросов загрязняющих веществ из различных источников оказывают на атмосферу. [4]
Турбулентное диффузионное пламя [ править ]
С использованием процессов плоской лазерно-индуцированной флуоресценции (PLIF) и измерения скорости изображения частиц (PIV) продолжаются исследования эффектов турбулентной диффузии в пламени. Основные области исследований включают системы сжигания в газовых горелках, используемых для выработки электроэнергии, и химические реакции в струйно-диффузионном пламени с участием метана (CH 4 ), водорода (H 2 ) и азота (N 2 ). [5] Кроме того, двухимпульсная визуализация температуры Рэлея использовалась для корреляции мест исчезновения и возгорания с изменениями температуры и смешиванием химических веществ в пламени. [6]
Моделирование [ править ]
Эйлеров подход [ править ]
Эйлеров подход к турбулентной диффузии фокусируется на бесконечно малом объеме в определенном пространстве и времени в фиксированной системе отсчета, в которой измеряются такие физические свойства, как масса, импульс и температура. [7] Модель полезна, потому что статистику Эйлера можно последовательно измерить и она отлично подходит для химических реакций. Подобно молекулярным моделям, он должен удовлетворять тем же принципам, что и приведенное ниже уравнение неразрывности, где адвекция элемента или разновидностей уравновешивается его диффузией, генерацией путем реакции и добавлением из других источников или точек, а также уравнениями Навье-Стокса :
Если мы рассматриваем инертные частицы (без реакции) без источников и предполагаем, что молекулярная диффузия незначительна, выживают только члены адвекции в левой части уравнения. Решение этой модели сначала кажется тривиальным, однако мы проигнорировали случайную составляющую скорости плюс среднюю скорость в u j = ū + u j ‘, которая обычно связана с турбулентным поведением. В свою очередь, концентрационное решение для модели Эйлера также должно иметь случайную составляющую c j = c + c j ‘. Это приводит к проблеме замыкания бесконечных переменных и уравнений и делает невозможным решение для определенного c i при указанных предположениях. [9]
К счастью, существует замыкающее приближение при введении концепции вихревой диффузии и ее статистических приближений для случайной концентрации и составляющих скорости от турбулентного перемешивания:
Подстановка в первое уравнение неразрывности и игнорирование реакций, источников и молекулярной диффузии приводит к следующему дифференциальному уравнению, учитывающему только приближение турбулентной диффузии в вихревой диффузии:
Лагранжев подход [ править ]
Затем можно рассчитать концентрацию частиц в точке x и времени t путем суммирования вероятностей количества наблюдаемых частиц следующим образом:
Что затем оценивается путем возврата к интегралу pdf
Таким образом, этот подход используется для оценки положения и скорости частиц относительно их соседей и окружающей среды и аппроксимирует случайные концентрации и скорости, связанные с турбулентной диффузией, в статистике их движения.
Решения [ править ]
Полученное решение для решения окончательных уравнений, перечисленных выше, для моделей Эйлера и Лагранжа для анализа статистики частиц в турбулентном потоке, обе приводят к очень похожим выражениям для расчета средней концентрации в месте от непрерывного источника. Оба решения образуют гауссовский плюм и практически идентичны при предположении, что отклонения в направлениях x, y, z связаны с коэффициентом диффузии вихрей:
куда σ y 2 = 2 K y y x u ¯ σ z 2 = 2 K z z x u ¯ <\displaystyle \sigma _
q = интенсивность выбросов видов, u = скорость ветра, σ i 2 = отклонение в i-м направлении. [8]
При различных внешних условиях, таких как скорость направленного потока (ветер) и условия окружающей среды, измеряются отклонения и коэффициенты диффузии турбулентной диффузии, которые используются для расчета точной оценки концентраций в определенной точке от источника. Эта модель очень полезна в науках об атмосфере, особенно при работе с концентрациями загрязняющих веществ в загрязнении воздуха, которые исходят из таких источников, как дымовые трубы, реки или автомобильные гусеницы на дороге. [2]
Будущие исследования [ править ]
Помимо этих усилий, до появления компьютеров были достигнуты успехи в полевых исследованиях. Теперь возможен мониторинг турбулентности, скорости и течений при перемешивании жидкостей в реальном времени. Это исследование оказалось важным для изучения циклов смешивания загрязняющих веществ в турбулентных потоках, особенно в системах питьевого водоснабжения.
ТУРБУЛЕНТНАЯ ДИФФУЗИЯ
ТУРБУЛЕНТНАЯ ДИФФУЗИЯ, перенос в-ва в пространстве, обусловленный турбулентным движением среды. Под турбулентным понимают вихревое движение жидкости или газа, при к-ром элементы (частицы) среды совершают неупорядоченные, хаотич. движения по сложным траекториям, а скорость, т-ра, давление и плотность среды испытывают хаотич. флуктуации.
Если в турбулентном потоке в определенный момент времени множество элементов (частиц) расположено рядом один с другим, то в послед, моменты времени они рассеиваются по пространству так, что статистич. расстояние между любыми двумя произвольными частицами с течением времени возрастает. Проявления этого процесса во многом напоминают мол. диффузию.
В основе описания турбулентной диффузии как процесса случайного блуждания частиц среды лежат выражения для среднеквадратичного смешения частиц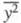
где 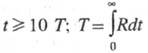
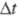
Поскольку турбулентная диффузия и мол. диффузия независимы, общее смещение частицы будет определяться суммой:
Т урбулентная диффузия протекает по-разному в зависимости от масштаба турбулентности. Перенос в-ва при маломасштабной турбулентности описывают по аналогии с мол. диффузией. При крупномасштабной турбулентности среднее квадратичное смещение частиц с течением времени быстро увеличивается, причем этот рост обусловлен преим. крупными вихрями.
Предполагают, что турбулентный перенос в-ва в рассматриваемый момент времени в произвольной точке пространства определяется градиентом осредненной концентрации, взятым в той же точке пространства и в тот же момент времени (гипотеза Буссинеска). Так, плотность турбулентного потока массы в направлении к.-л. из осей координат, напр. *, выражают в виде:
Используя соотношения, аналогичные законам вязкости Ньютона и теплопроводности Фурье (см. Переноса процессы), вводят коэф. турбулентной кинематич. вязкости v т и турбулентной температуропроводности а т (м 2 /с). Последние в отличие от выраженных в тех же единицах измерения коэф. мол. диффузии D, температуропроводности а и кинематич. вязкости v не являются физ.-хим. характеристиками и зависят от параметров осредненного движения среды, а также от положения рассматриваемого элемента ее объема в потоке.
В общем случае выражение для плотности диффузионного потока в бинарной жидкой или газовой смеси с учетом мол. и турбулентного механизмов переноса записывают в виде:
Знание закономерностей турбулентной диффузии необходимо при описании хим.-технол. процессов, протекающих в потоках жидкости или газа, в т. ч. в дисперсных средах. Турбулентная диффузия оказывает влияние на структуру потоков в аппаратах и вносит свой вклад в продольное и поперечное перемешивание в-ва. Чаще всего продольное перемешивание снижает движущую силу массо-обменных процессов и ухудшает их показатели.
Лит.: Mонин А. С., Яглом А. Я., Статистическая гидромеханика, ч. 1-2, M., 1967; Берд Р., Стыоарт В., Л айтфут E., Явления переноса, пер. с англ., M., 1974; Рейнольде А.Дж., Турбулентные течения в инженерных приложениях, M., 1979. В. В. Дильман.
Турбулентная диффузия
Однако было чрезвычайно сложно разработать конкретную и полностью функциональную модель, которую можно было бы применить к диффузии частиц во всех турбулентных системах из-за невозможности одновременно охарактеризовать как мгновенную, так и прогнозируемую скорость жидкости. В турбулентном потоке это является результатом нескольких характеристик, таких как непредсказуемость, быстрая диффузия, высокие уровни флуктуирующей завихренности и диссипация кинетической энергии. [2]
Содержание
Приложения [ править ]
Атмосферная диффузия и загрязнители [ править ]
Атмосферная дисперсия [3] или диффузия изучает, как загрязнители смешиваются в окружающей среде. В этот процесс моделирования включается множество факторов, таких как уровень атмосферы (-ов), в которой происходит перемешивание, стабильность окружающей среды и тип загрязняющего вещества и источника смешивания. Обе модели Эйлера и Лагранжа (обсуждаемые ниже) использовались для моделирования атмосферной диффузии и важны для правильного понимания того, как загрязнители реагируют и смешиваются в различных средах. Обе эти модели учитывают как вертикальный, так и горизонтальный ветер, но дополнительно интегрируют теорию диффузии Фика. для учета турбулентности. Хотя эти методы должны использовать идеальные условия и делать многочисленные допущения, на данный момент трудно лучше рассчитать влияние турбулентной диффузии на загрязнители. Теория диффузии Фика и дальнейшие достижения в исследованиях атмосферной диффузии могут быть применены для моделирования эффектов, которые текущие уровни выбросов загрязняющих веществ из различных источников оказывают на атмосферу. [4]
Турбулентное диффузионное пламя [ править ]
С использованием процессов плоской лазерно-индуцированной флуоресценции (PLIF) и измерения скорости изображения частиц (PIV) продолжаются исследования эффектов турбулентной диффузии в пламени. Основные области исследований включают системы сжигания в газовых горелках, используемых для выработки электроэнергии, и химические реакции в струйно-диффузионном пламени с участием метана (CH 4 ), водорода (H 2 ) и азота (N 2 ). [5] Кроме того, двухимпульсная визуализация температуры Рэлея использовалась для корреляции мест исчезновения и возгорания с изменениями температуры и смешиванием химических веществ в пламени. [6]
Моделирование [ править ]
Эйлеров подход [ править ]
Эйлеров подход к турбулентной диффузии фокусируется на бесконечно малом объеме в определенном пространстве и времени в фиксированной системе отсчета, в которой измеряются такие физические свойства, как масса, импульс и температура. [7] Модель полезна, потому что статистику Эйлера можно последовательно измерить и она отлично подходит для химических реакций. Подобно молекулярным моделям, он должен удовлетворять тем же принципам, что и приведенное ниже уравнение неразрывности, где адвекция элемента или разновидностей уравновешивается его диффузией, генерацией путем реакции и добавлением из других источников или точек, а также уравнениями Навье-Стокса :
Если мы рассматриваем инертные частицы (без реакции) без источников и предполагаем, что молекулярная диффузия незначительна, выживают только члены адвекции в левой части уравнения. Решение этой модели сначала кажется тривиальным, однако мы проигнорировали случайную составляющую скорости плюс среднюю скорость в u j = ū + u j ‘, которая обычно связана с турбулентным поведением. В свою очередь, концентрационное решение для модели Эйлера также должно иметь случайную составляющую c j = c + c j ‘. Это приводит к проблеме замыкания бесконечных переменных и уравнений и делает невозможным решение для определенного c i при указанных предположениях. [9]
К счастью, существует замыкающее приближение при введении концепции вихревой диффузии и ее статистических приближений для случайной концентрации и составляющих скорости от турбулентного перемешивания:
Подстановка в первое уравнение неразрывности и игнорирование реакций, источников и молекулярной диффузии приводит к следующему дифференциальному уравнению, учитывающему только приближение турбулентной диффузии в вихревой диффузии:
Лагранжев подход [ править ]
Затем можно рассчитать концентрацию частиц в точке x и времени t путем суммирования вероятностей количества наблюдаемых частиц следующим образом:
Что затем оценивается путем возврата к интегралу pdf
Таким образом, этот подход используется для оценки положения и скорости частиц относительно их соседей и окружающей среды и аппроксимирует случайные концентрации и скорости, связанные с турбулентной диффузией, в статистике их движения.
Решения [ править ]
Полученное решение для решения окончательных уравнений, перечисленных выше, для моделей Эйлера и Лагранжа для анализа статистики частиц в турбулентном потоке, обе приводят к очень похожим выражениям для расчета средней концентрации в месте от непрерывного источника. Оба решения образуют гауссовский плюм и практически идентичны при предположении, что отклонения в направлениях x, y, z связаны с коэффициентом диффузии вихрей:
куда σ y 2 = 2 K y y x u ¯ σ z 2 = 2 K z z x u ¯ <\displaystyle \sigma _
q = интенсивность выбросов видов, u = скорость ветра, σ i 2 = отклонение в i-м направлении. [8]
При различных внешних условиях, таких как скорость направленного потока (ветер) и условия окружающей среды, измеряются отклонения и коэффициенты диффузии турбулентной диффузии, которые используются для расчета точной оценки концентраций в определенной точке от источника. Эта модель очень полезна в науках об атмосфере, особенно при работе с концентрациями загрязняющих веществ в загрязнении воздуха, которые исходят из таких источников, как дымовые трубы, реки или автомобильные гусеницы на дороге. [2]
Будущие исследования [ править ]
Помимо этих усилий, до появления компьютеров были достигнуты успехи в полевых исследованиях. Теперь возможен мониторинг турбулентности, скорости и течений при перемешивании жидкостей в реальном времени. Это исследование оказалось важным для изучения циклов смешивания загрязняющих веществ в турбулентных потоках, особенно в системах питьевого водоснабжения.