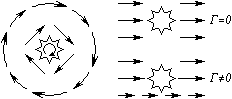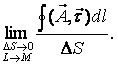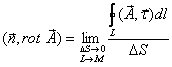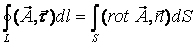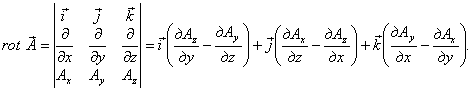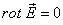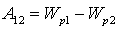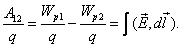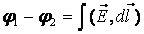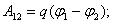Что такое циркуляция векторного поля
Скалярное и векторное поле. Циркуляция векторного поля вдоль кривой
Лекция 11.Скалярное и векторное поле. Циркуляция векторного поля вдоль кривой. Формула Грина.
Если в каждой точке М определенной пространственной области задано значение некоторой скалярной или векторной величины, то говорят, что задано поле этой величины (соответственно скалярное или векторное).
Примерами скалярных полей являются поле температур или поле электрического потенциала, примерами векторных полей – поле сил или поле скоростей.
Рассмотрим некоторые характеристики скалярных и векторных полей.
Определение 11.1. Если в некоторой области задано скалярное поле U(x,y,z), то поверхность, определяемая уравнением
называется поверхностью уровня. В двумерном случае линия уровня задается уравнением U(x, y) = C. (11.1`)
Определение 11.2. Если в некоторой области задано векторное поле 


Поверхность, составленная из векторных линий, называется векторной поверхно-стью. Если векторная поверхность образована векторными линиями, проходящими через каждую точку некоторой замкнутой кривой, то она называется векторной трубкой.
Определение 11.3. Пусть задано скалярное поле U(x, y, z). Вектор

называется градиентом величины U в соответствующей точке (см. лекцию 4 за 2-й семестр).
Замечание. Таким образом, скалярное поле U(x, y, z) порождает векторное поле градиента gradU.
Определение 11.4. Пусть дано векторное поле 

называется линейным интегралом от вектора 

Здесь 

Замечание. Иногда криволинейный интеграл 2-го рода по замкнутому контуру обозначают 
Пример. Вычислить циркуляцию векторного поля 
x² + y² = 9, z = 2 (направление обхода контура – от точки (3,0,2) к точке (0,3,2)).
Зададим контур L параметрически: x = 3cos t, y = 3sin t, z = 2 (0 ≤ t ≤ 2π). Тогда
Установим связь между двойным интегралом по некоторой плоской области D и криволинейным интегралом по границе L этой области.
Пусть в плоскости Оху дана ограниченная замкнутым контуром L правильная область D. Кривые, ограничивающие эту область снизу и сверху, заданы уравнениями
y = y1(x) и y = y2(x), y1(x) ≤ y2(x), a ≤ x ≤ b (рис.1).
Зададим в области D непрерывные функции P(x, y) и Q(x, y), имеющие непрерывные частные производные, и рассмотрим интеграл

Переходя к двукратному интегралу, получим:

Так как у = у2(х) – параметрическое выражение кривой МPN, то
где справа стоит криволинейный интеграл по кривой MPN. Аналогично получаем, что

Подставим полученные результаты в формулу (11.5):

так как контур L представляет собой объединение кривых MPN и NQM.
Так же можно получить, что 
Вычтем из равенства (11.6) равенство (11.7):
При этом обход контура L происходит по часовой стрелке. Изменим направление обхода. Тогда предыдущее равенство примет вид:

Эта формула, задающая связь между двойным интегралом и криволинейным интегралом 2-го рода, называется формулой Грина.
Замечание 1. Если в криволинейном интеграле по замкнутому контуру не указано направление обхода, то предполагается, что он производится против часовой стрелки.
Замечание 2. Если рассматривать в плоскости Оху векторное поле
Пример. Вычислим циркуляцию векторного поля
Применим формулу Грина, учитывая, что 

Лекция 5
1.Работа электрического поля
Из механики известно определение элементарной работы силы
Пусть в электрическом поле существует точечный заряд, который под действием поля перемещается из точки 1 в точку 2.
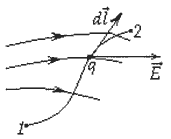
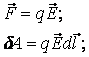
Считается, что заряд постоянный. Таким образом, работа равна криволинейному интегралу от напряженности, вычисленному вдоль траектории.
2.Работа в поле точечного заряда
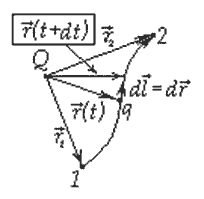
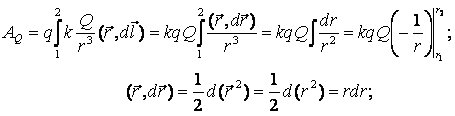
Очевидно, что данная работа не зависит от формы траектории, а зависит только от начального и конечного положения заряда. Можно сделать вывод о том, что если заряд перемещается по замкнутой траектории, то работа поля равна нулю. Таким образом, можно записать
3.Теорема о циркуляции
Пусть поле создано системой точечных зарядов. Вычислим интеграл от напряженности по замкнутой траектории.

Данное утверждение и составляет суть теоремы о циркуляции. В математике подобный интеграл называют циркуляцией.
 |
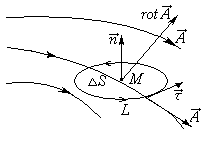
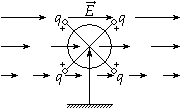
 | Циркуляцией вектора 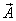 по произвольному замкнутому контуру L называется следующий криволинейный интеграл: по произвольному замкнутому контуру L называется следующий криволинейный интеграл:Здесь Существует соглашение, что положительное направление обхода контура (направление Так же, как и поток, циркуляция является ещё одной характеристикой свойств векторного поля. А именно, циркуляция характеризует степень завихренности векторного поля. Пример: если в качестве «измерителя» циркуляции поля скоростей жидкости можно взять турбинку, то если она вращается, циркуляция не равна нулю. Циркуляция – это интегральная характеристика поля. 5.Понятие ротораПоле по своей структуре может быть достаточно неоднородным. Циркуляция же не дает детальной характеристики поля. Следовательно, начнем стягивать контур интегрирования к какой-либо точке М (уменьшать турбину). Циркуляция при этом будет стремиться к нулю, но и площадь, охваченная контуром, также будет стремиться к нулю. А их отношение дает конечное число. Турбину можно ориентировать в пространстве тремя независимыми способами. Следовательно, таким способом можно получить 3 независимых числа, а три числа – это вектор, следовательно, образуется векторная характеристика поля, которая и называется ротором.
Ротор – это локальная или дифференциальная характеристика. 6.Формула СтоксаВ математике доказывается теорема Стокса, связывающая циркуляцию вектора с интегралом по поверхности, охваченной контуром интегрирования. 7.Выражение для ротора в декартовой системе координат8.Циркуляция и ротор в электростатикеИспользуя формулу Стокса можно показать, что ротор напряженности электрического равен нулю. — это теорема о циркуляции в дифференциальной форме. Заметим, что данная теорема справедлива только для электростатического поля. Если поле не статическое, то теорема не справедлива. В принципе измерить циркуляцию или ротор можно с помощью «электророторметра». 9.Потенциальная энергияИз механики известно, что если работа силы не зависит от формы траектории, то сила называется консервативной, а если работа поля по замкнутой траектории равна нулю, то поле называется потенциальным. Следовательно, кулоновская сила – это сила консервативная, а электростатическое поле – поле потенциальное. В связи с этим можно ввести понятие потенциальной энергии. 10.Разность потенциаловПоделим работу на заряд. Правая часть зависит только от самого поля. Следовательно, и левая часть также является характеристикой поля. Её называют разностью потенциалов.
|





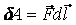
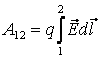
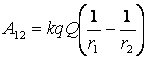
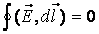
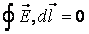
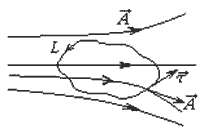
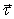 — единичный вектор, касательный к контуру в данной точке, направленный в сторону положительного обхода контура.
— единичный вектор, касательный к контуру в данной точке, направленный в сторону положительного обхода контура.