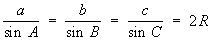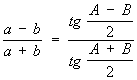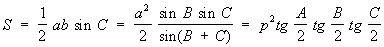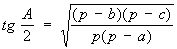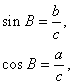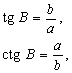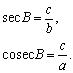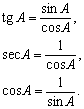что такое тригонометрия в математике

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

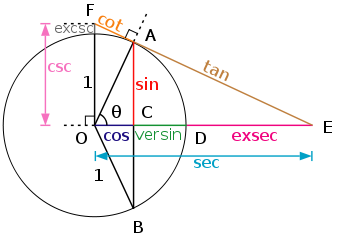
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

Принцип повтора знаков тригонометрических функций

Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.

В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.

Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.

Тригонометрический круг

Углы в радианах

Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.

Источник

Тригонометрия

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.

В Школе СССР имела статус учебного предмета.

Содержание

Определение тригонометрических функций

Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).

Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:

Для острых углов новые определения совпадают с прежними.

Возможно также чисто аналитическое определение этих функций, которое не связано с геометрией и представляет каждую функцию её разложением в бесконечный ряд.

История

Древняя Греция

Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.

Хотя в работах Евклида и Архимеда нет тригонометрии в строгом смысле этого слова, их теоремы представлены в геометрическом виде, эквивалентном специфическим тригонометрическим формулам. Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов. Для компенсации отсутствия таблицы хорд математики времен Аристарха иногда использовали хорошо известную теорему, в современной записи — sin α/ sin β Средневековая Индия

Другие источники сообщают, что именно замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.

Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как

Индийцы также знали формулы для кратных углов , , где .

Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.

Южноиндийские математики в 16 веке добивались больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа π. Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.

В 8 в. учёные стран Ближнего и Среднего Востока познакомились с трудами индийских математиков и астрономов и перевели их на арабский язык. В середине 9 века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того как арабские трактаты были переведены на латынь, многие идеи индийских математиков стали достоянием европейской, а затем и мировой науки.

Источник

Что такое тригонометрия в математике

При выполнении тригонометрических преобразований следуйте следующим советам:

Основные тригонометрические формулы

Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла. Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Дополнительные тригонометрические формулы

Тригонометрические формулы сложения. Синус суммы:

Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:

Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:

Произведение синуса и косинуса:

Формулы понижения степени. Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла. Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Тригонометрические формулы приведения

Функцию косинус называют кофункцией функции синус и наоборот. Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:

Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:

Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Решение тригонометрических уравнений в некоторых частных случаях:

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.

Источник

Тригонометрия

(от греч. trígōnon — треугольники …метрия (См. …метрия))

раздел математики, в котором изучаются Тригонометрические функции и их приложения к геометрии. Т. делится на плоскую, или прямолинейную, и сферическую тригонометрию (См. Сферическая тригонометрия). Теория тригонометрических функций (гониометрия) и её приложения к решению плоских прямоугольных и косоугольных треугольников изучаются в средней школе.

Основные формулы плоской Т. Пусть а, b, с — стороны треугольника, А, В, С — противолежащие им углы (А+В+С = π), h_a, h_b, h_c — высоты, 2p — периметр, S — площадь, 2R — диаметр окружности, описанной около треугольника. Теорема синусов:

Углы треугольника, если известны стороны, могут быть найдены по теореме косинусов или по формулам вида:

Плоская Т. начала развиваться позже сферической, хотя отдельные теоремы её встречались и раньше. Например, 12-я и 13-я теоремы второй книги «Начал» Евклида (3 в. дон. э.) выражают по существу теорему косинусов. Плоская Т. получила развитие у аль-Баттани (2-я половина 9 — начало 10 вв.), Абу-ль-Вефа (10 в.), Бхаскара (12 в.) и Насирэддина Туси (См. Насирэддин Туси) (13 в.), которым была уже известна теорема синусов. Теорема тангенсов была получена Региомонтаном (15 в.). Дальнейшие работы в области Т. принадлежат Н. Копернику (1-я половина 16 в.), Т. Браге (2—я половина 16 в.), Ф. Виету (16 в.), И. Кеплеру (конец 16 — 1-я половина 17 вв.). Современный вид Т. получила в работах Л. Эйлера (18 в.).

Лит.: Кочетков Е. С., Кочеткова Е. С., Алгебра и элементарные функции, ч. 1—2, М., 1966.

Источник

ТРИГОНОМЕТРИЯ

ТРИГОНОМЕТРИЯ – (от греч. trigwnon – треугольник и metrew – измеряю) – математическая дисциплина, изучающая зависимости между углами и сторонами треугольников и тригонометрические функции.

Термин «тригонометрия» ввел в употребление в 1595 немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. К концу 16 в. большинство тригонометрических функций было уже известно, хотя само это понятия еще не существовало.

В тригонометрии выделяют три вида соотношений: 1) между самими тригонометрическими функциями; 2) между элементами плоского треугольника (тригонометрия на плоскости); 3) между элементами сферического треугольника, т.е. фигуры, высекаемой на сфере тремя плоскостями, проходящими через ее центр. Тригонометрия началась именно с наиболее сложной, сферической части. Она возникла прежде всего из практических нужд. Древние наблюдали за движением небесных светил. Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников. По звездам вычисляли местонахождение корабля в море или направление движения каравана в пустыне. Наблюдения за звездным небом с незапамятных времен вели и астрологи.

Естественно, все измерения, связанные с расположением светил на небосводе, – измерения косвенные. Прямые могли быть проведены только на поверхности Земли, но и здесь далеко не всегда удавалось непосредственно определить расстояние между какими-то пунктами и тогда вновь прибегали к косвенным измерениям. Например, вычисляли высоту дерева, сравнивая длину его тени с длиной тени от какого-нибудь шеста, высота которого была известна. Аналогичным образом вычисляли и размеры острова в море. Подобные задачи сводятся к анализу треугольника, в котором одни его элементы выражают через другие. Этим и занимается тригонометрия. А поскольку звезды и планеты представлялись древним точками на небесной сфере, то сначала стала развиваться именно сферическая тригонометрия. Ее считали разделом астрономии.

А начиналось все очень давно. Первые отрывочные сведения по тригонометрии сохранились на клинописных табличках Древнего Вавилона. Астрономы Междуречья научились предсказывать положение Земли и Солнца и именно от них к нам пришла система измерения углов в градусах, минутах и секундах, потому что у вавилонян была принята шестидесятеричная система счисления.

Однако первые по-настоящему важные достижения принадлежат древнегреческим ученым. Например, 12-я и 13-я теоремы второй книги Начал Евклида (конец 4–3 в. до н. э.) выражают по существу теорему косинусов. Во 2 в. до н.э. астроном Гиппарх из Никеи (180–125 до н.э.) составил таблицу для определения соотношений между элементами треугольников. Такие таблицы нужны потому, что значения тригонометрических функций нельзя вычислить по аргументам с помощью арифметических операций. Тригонометрические функции приходилось рассчитывать заранее и хранить в виде таблиц. Гиппарх подсчитал в круге заданного радиуса длины хорд, отвечающих всем углам от 0 до 180°, кратным 7,5°. По существу, это таблица синусов. Труды Гиппарха до нас не дошли, но многие сведения из них включены в Альмагест (II в.) – знаменитое сочинение в 13 книгах греческого астронома и математика Клавдия Птолемея (ум. ок.160 н. э.). Древние греки не знали синусов, косинусов и тангенсов, вместо таблиц этих величин они употребляли таблицы, позволявшие находить хорду окружности по стягиваемой дуге. В Альмагесте автор приводит таблицу длин хорд окружности радиуса в 60 единиц, вычисленных с шагом 0,5° с точностью до 1/3600 единицы, и объясняет, как эта таблица составлялась. Труд Птолемея несколько веков служил введением в тригонометрию для астрономов.

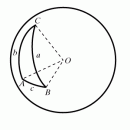
Чтобы понять, как ученые древности составляли тригонометрические таблицы, надо познакомиться с методом Птолемея. Метод основан на теореме – произведение диагоналей вписанного в окружность четырехугольника равно сумме произведений его противоположных сторон.

Пусть ABCD – вписанный четырехугольник, АD – диаметр окружности, а точка O – ее центр (рис. 1). Если известно, как вычислять хорды, стягивающие углы DOC = a и DОВ = b, т. е. сторону СD и диагональ B, то, по теореме Пифагора, из прямоугольных треугольников АDВ и АDС можно найти АВ и АС, а потом, по теореме Птолемея, – BC = (АС·ВD – АВ·СD) /АD, т.е. хорду, стягивающую угол ВОС = b – a. Некоторые хорды, например стороны квадрата, правильных шестиугольника и восьмиугольника, отвечающие углам 90, 60 и 45°, легко определить. Известна также сторона правильного пятиугольника, которая стягивает дугу в 72°. Приведенное выше правило позволяет вычислять хорды для разностей этих углов, например для 12° = 72° – 60°. Кроме того, можно находить хорды половинных углов, однако этого недостаточно, чтобы рассчитать, чему равна хорда дуги в 1°, – хотя бы потому, что все названные углы кратны 3°. Для хорды 1° Птолемей нашел оценку, показав, что она больше 2/3 хорды (3/2)° и меньше 4/3 хорды (3/4)° – двух чисел, совпадающих с достаточной для его таблиц точностью.

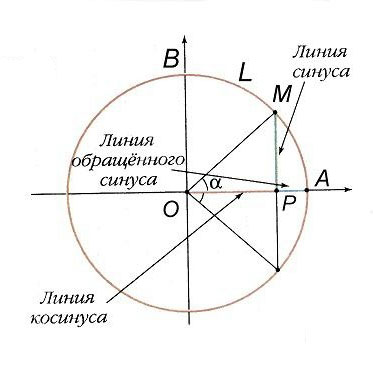
Если греки по углам вычисляли хорды, то индийские астрономы в сочинениях 4–5 вв. перешли к полухордам двойной дуги, т.е. в точности к линиям синуса (рис. 2). Они пользовались и линиями косинуса – вернее, не его самого, а «обращенного» синуса, получившего позднее в Европе название «синус-верзус», сейчас эта функция, равная 1 – cos a, уже не употребляется. Впоследствии тот же подход привел к определению тригонометрических функций через отношения сторон прямоугольного треугольника.

За единицу измерения отрезков MP, OP, PA принималась дуговая минута. Так, линия синуса дуги AB = 90° есть OB – радиус окружности; дуга AL, равная радиусу, содержит (округленно) 57°18′ = 3438′.

Дошедшие до нас индийские таблицы синусов (древнейшая составлена в 4–5 веке н.э.) не столь точны, как птолемеевы; они составлены через 3°45′ (т.е. через 1/24 часть дуги квадранта).

Термины «синус» и «косинус» пришли от индийцев, не обошлось и без любопытного недоразумения. Полухорду индийцы называли «ардхаджива» (в переводе с санскрита – «половина тетивы лука»), а потом сократили это слово до «джива». Мусульманские астрономы и математики, получившие знания по тригонометрии от индийцев, восприняли его как «джиба», а затем оно превратилось в «джайб», что на арабском языке означает «выпуклость», «пазуха». Наконец, в 7 в. «джайб» буквально перевели на латынь словом «sinus», которое не имело никакого отношения к обозначаемому им понятию. Санскритское «котиджива» – синус остатка (до 90°), а на латинском – sinus complementi, т.е. синус дополнения, в 17 в. сократилось до слова «косинус». Наименования «тангенс» и «секанс» (в переводе с латинского означающие «касательная» и «секущая») введены в 1583 немецким ученым Финком.

Большой вклад в развитие тригонометрии внесли арабские ученые, например, Аль-Баттани (ок. 900 н.э.). В 10 в. багдадский ученый Мухаммед из Буджана, известный под именем Абу-ль-Вефа (940–997), присоединил к линиям синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов. Он дает им те же определения, которые содержатся и в наших учебниках. Абу-ль-Вефа устанавливает и основные соотношения между этими линиями.

Итак, к концу 10 в. ученые исламского мира уже оперировали, наряду с синусом и косинусом, четырьмя другими функциями – тангенсом, котангенсом, секансом и косекансом; открыли и доказали несколько важных теорем плоской и сферической тригонометрии; использовали окружность единичного радиуса (что позволило толковать тригонометрические функции в современном смысле); придумали полярный треугольник сферического треугольника. Арабские математики составили точные таблицы, например таблицы синусов и тангенсов с шагом в 1′ и точностью до 1/700 000 000. Очень важной прикладной задачей была и такая: научиться определять направление на Мекку для пяти ежедневных молитв, где бы ни находился мусульманин.

Особенно большое влияние на развитие тригонометрии оказал Трактат о полном четырехстороннике астронома Насир-эд-Дин из Туса (1201–1274), известного так же под именем ат-Туси. Это было первое в мире сочинение, в котором тригонометрия трактовалась как самостоятельная область математики.

В 12 в. был переведен с арабского языка на латинский ряд астрономических работ, по ним впервые европейцы познакомились с тригонометрией.

Трактат Насир-эд-Дина произвел большое впечатление на немецкого астронома и математика Иоганна Мюллера (1436–1476). Современники больше знали его под именем Региомонтана (так переводится на латинский название его родного города Кенигсберга, ныне – Калининграда). Региомонтан составил обширные таблицы синусов (через 1 минуту с точностью до седьмой значащей цифры). Он впервые отступил от шестидесятиричного деления радиуса и за единицу измерения линии синуса принял одну десятимиллионную часть радиуса. Таким образом, синусы выражались целыми числами, а не шестидесятиричными дробями. До введения десятичных дробей оставался только один шаг, но он потребовал более 100 лет. Труд Региомонтана О треугольниках всех родов пять книг сыграл в европейской математике ту же роль, что и сочинение Насир-эд-Дина в науке мусульманских стран.

За таблицами Региомонтана последовал ряд других, еще более подробных. Друг Коперника Ретик (1514–1576) вместе с несколькими помощниками в течение 30 лет работал над таблицами, законченными и изданными в1596 его учеником Отто. Углы шли через 10», а радиус делился на 1 000 000 000 000 000 частей, так что синусы имели 15 верных цифр.

Дальнейшее развитие тригонометрии шло по пути накопления и систематизации формул, уточнения основных понятий, становления терминологии и обозначений. Многие европейские математики работали в области тригонометрии. Среди них такие великие ученые, как Николай Коперник (1473–1543), Тихо Браге (1546–1601) и Иоганн Кеплер (1571–1630). Франсуа Виет (1540–1603) дополнил и систематизировал различные случаи решения плоских и сферических треугольников, открыл «плоскую» теорему косинусов и формулы для тригонометрических функций от кратных углов. Исаак Ньютон (1643–1727) разложил эти функции в ряды и открыл путь для их использования в математическом анализе. Леонард Эйлер (1707–1783) ввел и само понятие функции, и принятую в наши дни символику. Величины sin x, cos x и т.д. он рассматривал как функции числа x – радианной меры соответствующего угла. Эйлер давал числу x всевозможные значения: положительные, отрицательные и даже комплексные. Он также обнаружил связь между тригонометрическими функциями и экспонентой комплексного аргумента, что позволило превратить многочисленные и зачастую весьма замысловатые тригонометрические формулы в простые следствия из правил сложения и умножения комплексных чисел. Он же ввел и обратные тригонометрические функции.

К концу 18 в. тригонометрия как наука уже сложилась. Тригонометрические функции нашли применение в математическом анализе, физике, химии, технике – везде, где приходится иметь дело с периодическими процессами и колебаниями – будь то акустика, оптика или качание маятника.

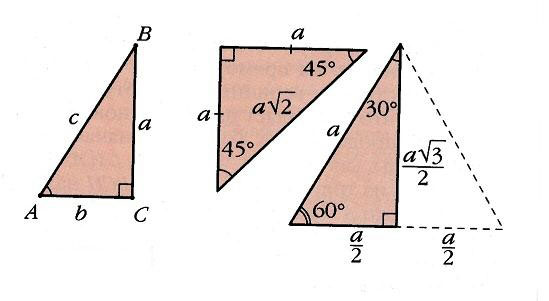
Решение любых треугольников, в конечном счете, сводится к решению прямоугольных треугольников (т.е. таких, у которых один из углов – прямой). Поскольку все прямоугольные треугольники с заданным острым углом подобны друг другу, отношения их соответственных сторон одинаковы. Например, в прямоугольном треугольнике ABC отношение двух его сторон, например, катета а к гипотенузе с, зависит от величины одного из острых углов, например А. Отношения различных пар сторон прямоугольного треугольника и называются тригонометрическими функциями его острого угла. Всего таких отношений в треугольнике шесть, и им отвечают шесть тригонометрических функций (обозначения сторон и углов треугольника на рис. 3).

Синус 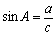(отношение противолежащего катета к гипотенузе),

косинус 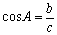(отношение прилежащего катета к гипотенузе),

тангенс 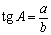(отношение противолежащего катета к прилежащему),

котангенс 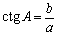(отношение прилежащего катета к противолежащему),

секанс sec A = 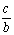(отношение гипотенузы к прилежащему катету),

косеканс cosec A = 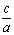(отношение гипотенузы к противолежащему катету).

По отношению к углу B («дополнительному» углу по отношению к А) формулы меняются соответственно:

Из определений вытекает несколько равенств, связывающих тригонометрические функции одного и того же угла между собой:

С учетом теоремы Пифагора a 2 + b 2 = c 2 можно выразить все шесть функций через какую-нибудь одну. Например, синус и косинус связаны основным тригонометрическим тождеством

Некоторые соотношения между функциями:

Эти формулы справедливы и для тригонометрических функций любого угла, но ими надо пользоваться осторожно, поскольку правые и левые части могут иметь разные области определения.

Есть только два прямоугольных треугольника, у которых и углы «хорошие» (выражаются целым или рациональным числом градусов), и хотя бы одно из отношений сторон рационально. Это равнобедренный треугольник (с углами 45, 45 и 90°) и половина равностороннего треугольника (с углами 30, 60, 90°) – как раз те два случая, когда значения тригонометрических функций удается вычислить прямо по определению. Эти значения приведены в таблице

Источник