что такое трехмерное измерение что это такое
Трёхмерное пространство
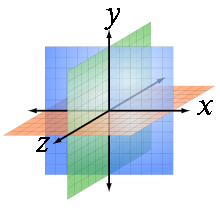
Трёхме́рное простра́нство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так как оно имеет три однородных измерения — высоту, ширину и длину, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.
Понимание трёхмерного пространства людьми, как считается, развивается ещё в младенчестве, и тесно связано с координацией движений человека. Визуальная способность воспринимать окружающий мир органами чувств в трёх измерениях называется глубиной восприятия.
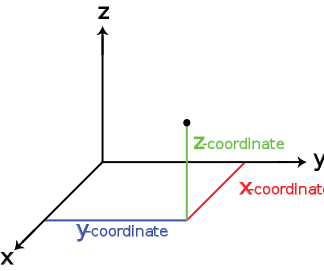
В аналитической геометрии каждая точка трёхмерного пространства описывается как набор из трёх величин — координат. Задаются три взаимно перпендикулярных координатных оси, пересекающихся в начале координат. Положение точки задаётся относительно этих трёх осей заданием упорядоченной тройки чисел. Каждое из этих чисел задаёт расстояние от начала отсчёта до точки, измеренное вдоль соответствующей оси, что равно расстоянию от точки до плоскости, образованной другими двумя осями.
Другой взгляд даёт линейная алгебра, где важную роль играет понятие линейной независимости. Пространство трёхмерно по той причине, что высота коробки не зависит от её длины и ширины. На языке линейной алгебры пространство трёхмерно, потому что каждая точка может быть задана комбинацией из трёх линейно независимых векторов. В этих терминах пространство-время четырёхмерно, потому что положение точки во времени не зависит от её положения в пространстве.
Нульмерное, одномерное и двухмерное пространства могут рассматриваться как располагающиеся в трёхмерном пространстве; само оно может считаться частью модели четырёхмерного пространства (четвёртым измерением континуума, как правило, называют время — неоднородное качество по отношению к пространственной мерности). [3]
Трёхмерное пространство
Понимание трёхмерного пространства людьми, как считается, развивается ещё в младенчестве, и тесно связано с координацией движений человека. Визуальная способность воспринимать окружающий мир органами чувств в трёх измерениях называется восприятием глубины.
В аналитической геометрии каждая точка трёхмерного пространства описывается как набор из трёх величин — координат. Задаются три взаимно перпендикулярных координатных оси, пересекающихся в начале координат. Положение точки задаётся относительно этих трёх осей заданием упорядоченной тройки чисел. Каждое из этих чисел задаёт расстояние от начала отсчёта до точки, измеренное вдоль соответствующей оси, что равно расстоянию от точки до плоскости, образованной другими двумя осями.
Также существуют другие системы координат, наиболее часто используются цилиндрическая и сферическая системы.
Другой взгляд даёт линейная алгебра, где важную роль играет понятие линейной независимости. Пространство трёхмерно по той причине, что высота коробки не зависит от её длины и ширины. На языке линейной алгебры пространство трёхмерно, потому что каждая точка может быть задана комбинацией из трёх линейно независимых векторов. В этих терминах пространство-время четырёхмерно, потому что положение точки во времени не зависит от её положения в пространстве.
Трёхмерное пространство имеет несколько свойств, которые отличают его от пространств другой размерности. Например, это пространство наименьшей размерности, в котором можно завязать узел на куске верёвки. Многие законы физики, например многие законы обратных квадратов связаны с тем что размерность нашего пространства три.
Нульмерное, одномерное и двухмерное пространства могут рассматриваться как располагающиеся в трёхмерном пространстве; само оно может считаться частью модели четырёхмерного пространства (четвёртым измерением иногда называют время).
Трехмерный мир, в котором мы не живем
Еще древние греки превратили математику из эмпирической науки в дедуктивную, потребовав вывода доказательств ее утверждений из основных понятий и исключив ссылку на опыт в качестве аргумента.
Чистая математика исследует формы и отношения в отвлечении от материального содержания. Ее непосредственным предметом оказываются, например, не те или иные тела шарообразной формы, а «идеальный шар», не те или иные совокупности предметов и даже не отдельные числа, а целые числа вообще и т. п.
Однако при всей абстрактности этой науки никто из математиков, по-видимому, не сомневался в том, что все их понятия, теоремы и формулы выражают реальные количественные и пространственные отношения. Математическая геометрия была теорией реального пространства, как позже механика явилась теорией движения
Математика — наука, изучающая
количественные и пространственные
формы и отношения действительности
Академик А. Д. Александров
Окружающий нас мир трехмерен. Мы привыкли к этой мысли с рождения — каждый человек знает, что такое высота, длина и ширина, три основных измерения окружающего нас пространства. В зависимости от традиций, принятых в разных странах, размеры предметов измеряют в метрах, футах, ли, лье и других эталонных единицах длины. Для наших дальнейших рассуждений выберем немного необычную единицу длины. Ею будет служить один световой год (1 св. г.), т. е. расстояние, проходимое лучом света за один календарный год. В традиционных мерах длины это составляет невообразимую величину — примерно 9,46•10 12 километров.
Если из окружающего нас пространства мысленно вырезать куб с ребром, равным 1 св. году, то внутри благополучно разместится дом, в котором мы живем, земной шар, Солнечная система… В общем, все, что необходимо для нормальной жизни человека. Для удобства назовем рассмотренный нами куб единичным кубом. А теперь отметим следующий очевидный факт. Несмотря на громадные размеры, наш единичный куб — лишь мельчайшая частица окружающего мира.
Кстати сказать, в этом определении размеры самого куба не задаются — вовсе не обязательно использовать кубы больших размеров. С таким же успехом можно утверждать, что каждая точка содержится в кубе, ребро которого не превосходит по длине, скажем, один микрон (10 —6 см).
Все сказанное выше кратко можно выразить следующими словами: окружающий нас мир является трехмерным евклидовым многообразием. А теперь попробуем ответить на следующий вопрос: как устроен мир за пределами единичного куба, в котором находится наш дом — наша Солнечная система?
Трехмерный тор и другие
Если на минуту вообразить, что окружающее нас пространство бесконечно по всем направлениям, то ответ на вопрос о строении окружающего нас мира даст следующая теорема Адамара:
«Бесконечно протяженное по всем направлениям трехмерное евклидово многообразие М 3 совпадает с евклидовым пространством E 3 ».
Евклидово пространство Е 3 с прямоугольной системой координат всем хорошо известно, поэтому не будем подробно останавливаться на изучении его свойств.
Для того же, чтобы сделать наши рассуждения более содержательными и интересными, предположим другой вариант: окружающий нас мир замкнут, т. е. имеет конечные размеры и не имеет края. Другими словами, зададимся вопросом, как устроены замкнутые трехмерные евклидовы многообразия, или, другими словами, евклидовы формы. Полный ответ на этот вопрос дает теорема, доказанная Дж. Вольфом (1982):
Существует ровно десять трехмерных евклидовых форм. Причем шесть из них представляют собой ориентируемые, а остальные четыре — неориентируемые многообразия.
Все евклидовые формы строятся схожим образом, единственное — для построения некоторых из них нужно использовать куб, а для других — правильную шестиугольную призму.
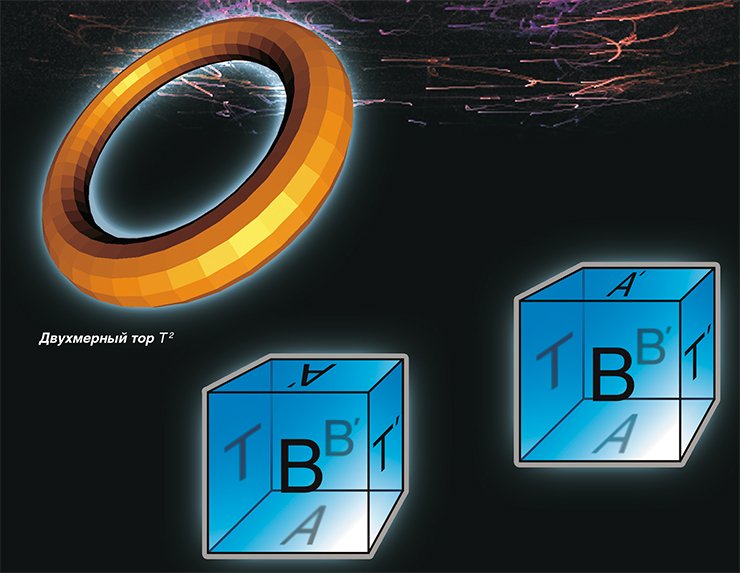
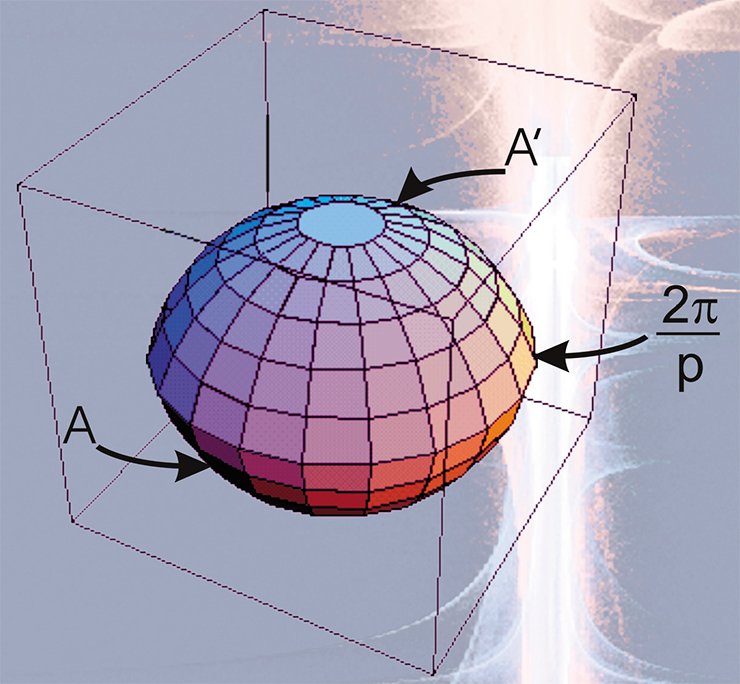
Для этого в центре грани А трехмерного тора поместим космический корабль, летящий со скоростью света, и заставим его стартовать в вертикальном направлении. Ровно через год космический корабль, продолжая двигаться по прямой, вернется в исходную точку. Теперь эта точка будет находиться в центре грани А’, которая, по условию, отождествлена с гранью А. В результате эксперимента обнаружим, что в трехмерном торе Т 3 существует замкнутая прямая линия l длиной в один световой год.
Поставим еще один аналогичный эксперимент. Заставим космический корабль стартовать из точки у, лежащей в грани А на расстоянии 1 км от ее центра. Через год корабль благополучно вернется в точку у. Вывод из второго эксперимента — через точку у проходит замкнутая прямая длиной 1 световой год, параллельная прямой l.
Многообразные многообразия
Как уже было замечено, все рассмотренные выше многообразия обладают евклидовой геометрией. Что это означает и какие еще геометрии существуют?
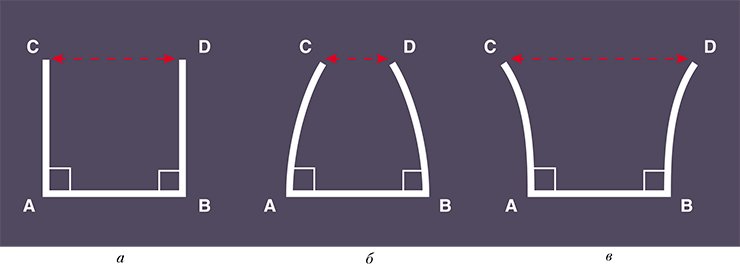
Наиболее известными и употребимыми в общечеловеческой практике являются евклидова, сферическая и гиперболическая геометрии. Напомним, что сферическую геометрию иногда называют геометрией Римана, а гиперболическую — геометрией Лобачевского. В трехмерном пространстве, кроме трех указанных, существует еще пять так называемых синтетических геометрий.
В соответствии с тем, какие геометрические законы действуют на трехмерном многообразии, будем называть его соответственно евклидовым, сферическим, гиперболическим или синтетическим.
Евклидовы многообразия мы уже рассмотрели выше. Что до остальных, то более двадцати лет назад У. Терстон (1978) доказал замечательную теорему: почти все трехмерные многообразия являются гиперболическими, то есть подчиняются законам геометрии Лобачевского. За этот результат в 1983 году он был удостоен Филдсовской премии — самой престижной награды для математиков.
Сферические многообразия бывают как трехмерные, так и многомерные (Вольф, 1982). В пространстве любой размерности существует конечное число типов таких многообразий. Синтетических многообразий очень мало (Thurston, 1978; Dunbar, 1981; Терстон, 2001) в отличие от оставшегося класса гиперболических многообразий. Последний неисчерпаемо широк и классификация его к настоящему времени не завершена.
Сферические многообразия
Все трехмерные сферические многообразия — ориентируемы. Это означает, что по какой бы замкнутой траектории не летал космический корабль с непрерывно вращающимся пропеллером, по возвращении в точку старта его пропеллер вращается в ту же сторону, что и в момент старта.
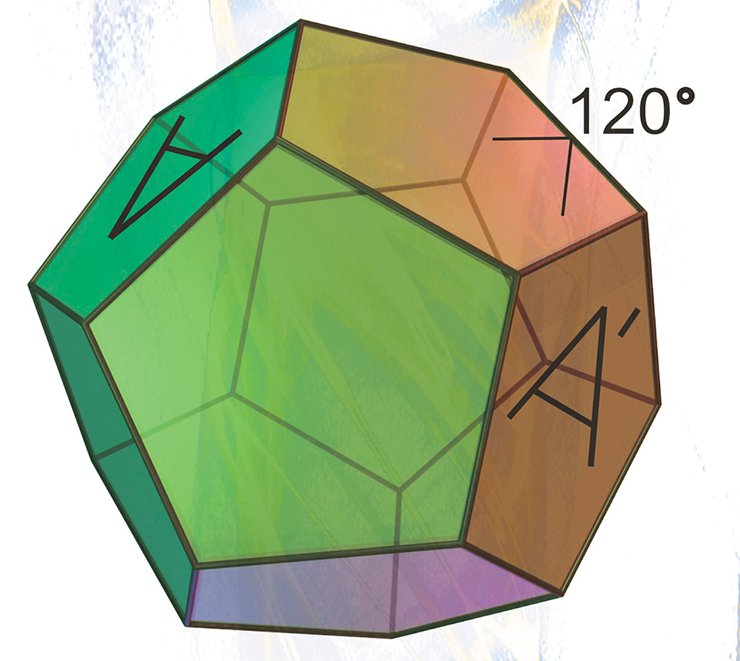
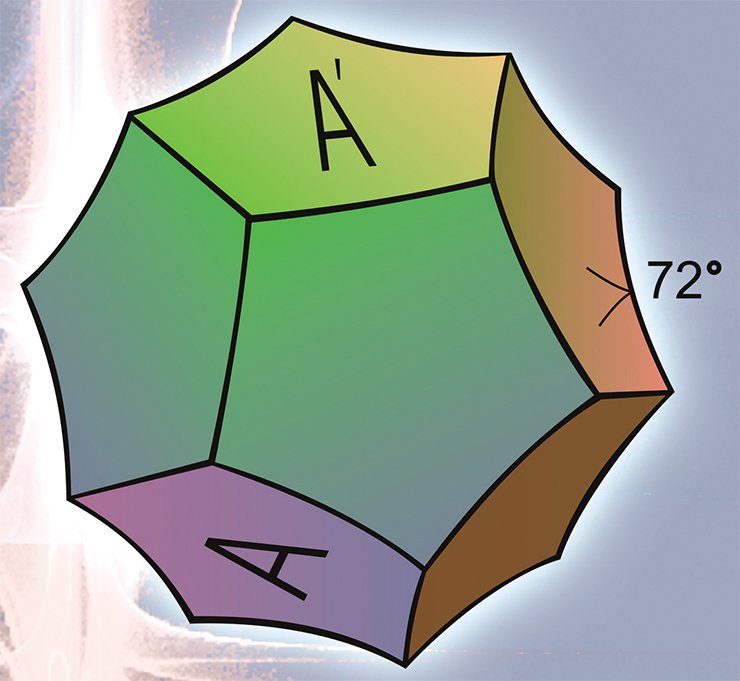
Третий, и пожалуй, самый нетривиальный пример сферического многообразия — сферическое пространство додекаэдра Пуанкаре или, для краткости, сфера Пуанкаре.
Сфера Пуанкаре удивительным образом связана с самыми различными разделами математики — геометрией, топологией, теорией групп, теорией катастроф, теорией узлов и другими (Кирби, Шарлеман, 1982).
Все остальные сферические многообразия, получаемые по единой схеме, представляют собой так называемые линзовые и призматические пространства.
Гиперболические многообразия
Первое трехмерное замкнутое гиперболическое многообразие было построено немецким математиком Ф. Лебеллем в 1931 г. Однако построение его было достаточно сложным, поэтому двумя годами позже Х. Зейферт и К. Вебер предложили элегантную конструкцию гиперболического пространства додекаэдра.
С точки зрения математики наиболее сложная часть проблемы построения состоит в доказательстве существования этого гиперболического додекаэдра в пространстве Лобачевского. Положительный ответ на этот вопрос дает фундаментальная теорема Е. М. Андреева (1970), в которой сформулированы необходимые и достаточные условия для существования выпуклых гиперболических многогранников. Эта теорема служит одним из краеугольных камней современной теории гиперболических многообразий, созданной У. Терстоном.
Конструируем многообразия из многогранников
Рассмотрим прямоугольный многогранник Р, все двугранные (и плоские) углы которого равны 90°. В евклидовом пространстве в качестве такого многогранника можно взять куб, в сферическом — тетраэдр, а в гиперболическом — шестиугольную призму Лебелля, боковая поверхность которой состоит из 12-ти пятиугольников.
Из теоремы Андреева следует, что любой многогранник, у которого нет треугольных и четырехугольных граней, а в каждой вершине сходится ровно по три ребра, может быть реализован как прямоугольный многогранник в пространстве Лобачевского. Шестиугольная призма Лебелля, очевидно, удовлетворяет этим условиям.
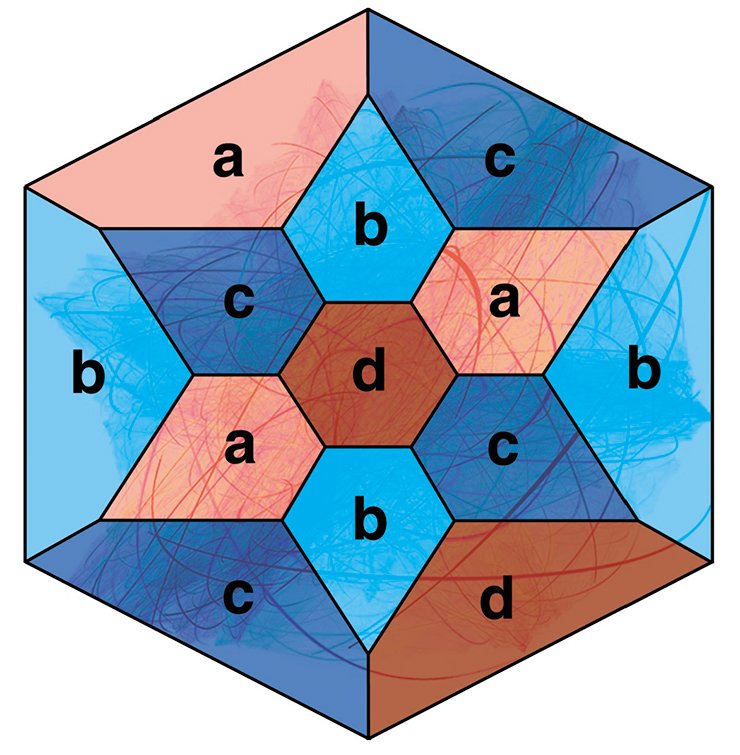
Для построения гиперболических многообразий используется способ, заключающийся в окраске смежных граней многогранника в разные цвета и последующего отождествления соответствующих граней, окрашенных в один цвет, у нескольких одинаковых экземпляров многогранников. Такой способ построения многообразий был впервые реализован Ф. Лебеллем (Loebell, 1931) для шестиугольной призмы, японским математиком М. Такахаши (Takahashi, 1985) — для правильного прямоугольного додекаэдра и А. Ю. Весниным (1987) — для произвольного прямоугольного многогранника Р.
При этом отметим, что все многообразия, построенные по окраске многогранника в четыре цвета, ориентируемы. Однако доказано, что окрашивая грани многогранника Р в пять, шесть или семь цветов, по аналогичной схеме можно построить и неориентируемые многообразия (Mednykh, 1992).
Остановимся еще на одном свойстве прямоугольных многогранников. Пусть D — правильный прямоугольный додекаэдр в пространстве Лобачевского. Испанский математик Х.-М. Монтезинос (Hilden et al., 1987) доказал следующую замечательную теорему:
«Любое замкнутое трехмерное многообразие может быть получено из конечного числа экземпляров многогранника D попарным отождествлением их граней».
Отметим, что в теореме Монтезиноса все грани склеенных многогранников — конгруэнтны, а все ребра имеют одинаковую длину. При этом каждое ребро окружено четырьмя, двумя или одним додекаэдром. Первую ситуацию легко представить: четыре прямоугольных додекаэдра склеены друг за другом вокруг общего ребра и образуют суммарный угол, равный 4•90° = 360°. Во втором случае пара смежных граней одного додекаэдра отождествляется с парой смежных граней другого додекаэдра. Суммарный двугранный угол вокруг ребра, принадлежащего двум додекаэдрам, в этом случае равен 2•90° = 180°. Третий вариант легко создать, отождествляя смежные грани одного додекаэдра поворотом на угол 90°.
Наличие ребер второго и третьего типа превращает многообразие в многообразие с особенностями, или орбифолд. В этом случае указанные ребра образуют сингулярное множество орбифолда. Заметим, что всюду, кроме сингулярных ребер, многообразие обладает геометрией Лобачевского.
Трехмерные орбифолды
Евклидовы орбифолды
Для всякого трехмерного евклидова орбифолда существует фундаментальное множество — криволинейный многогранник, из которого заданный орбифолд можно получить, попарно отождествляя (склеивая) определенные его грани.
Примерами евклидовых орбифолдов могут служить так называемые Борромеевы кольца или трехмерная сфера с сингулярным множеством узел «восьмерка».
Всего существует 230 замкнутых трехмерных евклидовых орбифолдов — по числу кристаллографических групп, открытых в конце прошлого века русским ученым Е. С. Федоровым. Строение евклидовых орбифолдов было полностью описано в докторской диссертации У. Данбара, защищенной в 1981 г. в Принстонском университете — крупнейшем математическом центре мира.
Сферические орбифолды
Сингулярным множеством сферических орбифолдов может служить так называемый рациональный узел или зацепление. Им может оказаться также заузленный граф, из каждой вершины которого выходит по три ребра. В частности, сингулярным множеством сферического орбифолда будет являться скелет тетраэдра (ребра + вершины), расположенный в трехмерной сфере.
q > l. В сферическом пространстве S ³ рассмотрим линзу с углом, равным π/р и поделим ее ребро точками 1,2. 2р на 2р равных частей. Соединим пары точек <р, 2р>и
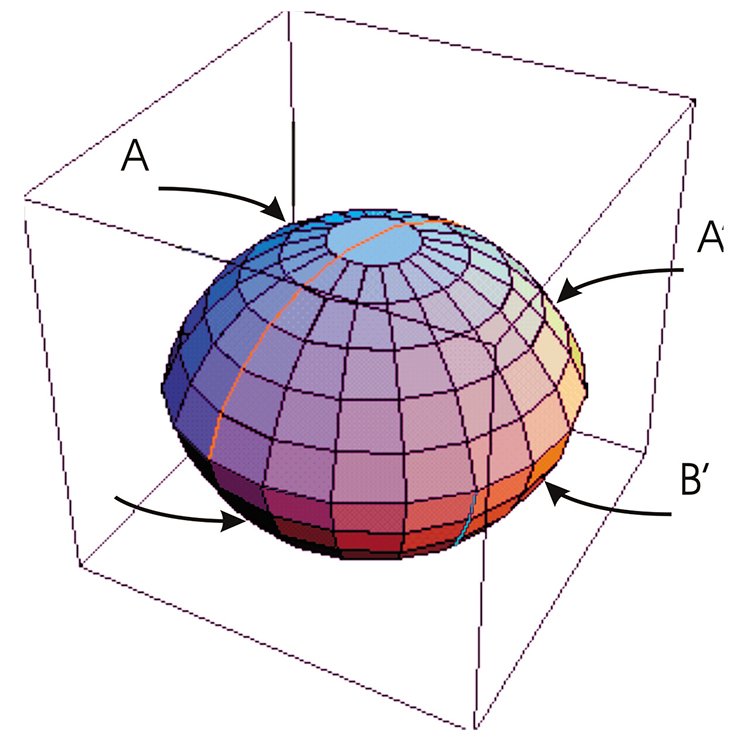
При этом следует иметь ввиду, что сильные заузливания тетраэдра могут испортить сферическую геометрию и заставить орбифолд обладать евклидовой, гиперболической или одной из синтетических геометрий.
Недавно австралийцами профессором К. Ходжсоном и его учеником Д. Хеардом создана компьютерная программа, позволяющая вычислять объемы заузленных графов, вложенных в трехмерную сферу (Hodgson and Heard, 2005). Полная классификация трехмерных орбифолдов во всех геометриях, кроме гиперболической, сделана в работах У. Данбара. Как и в случае многообразий, гиперболическая геометрия является наиболее богатой, и полное описание орбифолдов в ней до сих пор не получено.
Гиперболические орбифолды
Из теоремы Монтезиноса следует, что каждое трехмерное многообразие может быть превращено в гиперболический орбифолд, если внутрь его поместить подходящее сингулярное множество. Поскольку существует бесконечно много различных многообразий, отсюда следует, что существует также бесконечно много гиперболических орбифолдов.
Один из простейших гиперболических орбифолдов — трехмерная сфера с сингулярным множеством Борромеевы кольца с индексом сингулярности 4. Другой пример — сильно заузленный тетраэдр, все ребра которого имеют индекс сингулярности два. Доказательство таких фактов обычно достаточно сложно и может быть проведено с помощью теорем о геометризации, полученных У. Терстоном, его учениками и последователями. Общий принцип доказательства состоит в следующем: если орбифолд не является евклидовым, сферическим или синтетическим и удовлетворяет некоторым простым геометрическим условиям, то он — гиперболический.
Изменения, произошедшие в математике за последние более чем полтора века, не только необозримо расширили ее содержание, но и изменили его принципиально. В предмет математики сейчас входит любая структура, которую можно исследовать путем логического рассуждения с достаточной строгостью и богатством выводов. Найдет ли она применение и прообраз в действительности — это уже вопрос не к математике.
Понятно, что фактически наибольшее развитие получают те теории, которые находят существенные применения в самой математике и тем более за ее пределами. Хотя опыт развития науки уже достаточное число раз показал, как самые отвлеченные теории находили потом чрезвычайно существенные приложения. Но для самой чистой математики это в принципе безразлично. Лучше всего творческое кредо новой математики выразил создатель теории множеств Г. Кантор, гордо зявив: «Сущность математики. в ее свободе».
Винберг Э. Б. О неевлидовой геометрии, Соросовский образовательный журнал, № 3, 1996, С. 104—109.
Тёрстон У. Трехмерная геометрия и топология, М: МЦНМО, 2001 (Перевод с англ. под ред. О. В. Шварцмана).
Hodgson C., Heard D. Computer program “Orb”, August 2005, http://www.ms.unimelb.edu.au/
Работа поддержана грантом РФФИ (№ 06-01-00153) и INTAS (№ 03-01-3663)
Автор и редакция выражает искреннюю благодарность Н. В. Абросимову (вед. инженеру Института математики им. С. Л. Соболева СО РАН, студенту 6-го курса НГУ), оказавшему неоценимую помощь при подготовке публикации
Многомерные пространства — 3D, 4D и другие измерения
Илья Щуров, Jason Hise, ashgrowen, Анатолий Белов
Многомерные пространства
Что такое четырёхмерное пространство («4D»)?
Представление других измерений
Что такое гиперкуб? Построение тессеракта
Виды гиперкубов и их названия
Как насчет 10D?
Многомерные пространства — миф или реальность? Большинству из нас, или, возможно, всем нам невозможно представить мир, состоящий из более чем трех пространственных измерений. Правильно ли утверждение, что такой мир не может существовать? Или просто человеческий разум не способен вообразить дополнительные измерения — измерения, которые могут оказаться такими же реальными, как и другие вещи, которые мы не можем увидеть?
Мы достаточно часто слышим что-нибудь вроде «трехмерное пространство», или «многомерное пространство», или «четырехмерное пространство». Возможно, вы знаете, что мы живем в четырехмерном пространстве-времени. Что это означает и почему это интересно, почему математики и не только математики изучают такие пространства?
Об авторах
Илья Щуров — кандидат физико-математических наук, доцент кафедры высшей математики НИУ ВШЭ.
Jason Hise — Physics programmer at Ready at Dawn Studios, 4D geometry enthusiast. Автор анимированных моделей, представленных в данной статье.
ashgrowen — пикабушник, проиллюстрировавший в этой статье построение тессеракта и гиперкуба.
Давайте начнем с простого — начнем с одномерного пространства. Представим себе, что у нас есть город, который расположен вдоль дороги, и в этом городе есть только одна улица. Тогда мы можем каждый дом на этой улице закодировать одним числом — у дома есть номер, и этот номер однозначно определяет, какой дом имеется в виду. Люди, которые живут в таком городе, — можно считать, что они живут в таком одномерном пространстве. Жить в одномерном пространстве довольно скучно, и люди обычно живут не в одномерном пространстве.
Например, если мы говорим про города, то можно перейти от одномерного пространства к двумерному. Примером двумерного пространства является плоскость, а если мы продолжим нашу аналогию с городами, то это город, в котором можно расчертить улицы, допустим, перпендикулярно друг другу, как это сделано в Нью-Йорке, в центре Нью-Йорка. Там есть «стрит» и авеню, каждая из которых имеет свой номер, и вы можете задавать местоположение на плоскости, задавать два числа. Опять же, все мы знаем декартову систему координат, знакомую со школы, — каждая точка задается двумя числами. Это пример двумерного пространства.
Но если мы говорим про город типа центра Нью-Йорка, то на самом деле он является трехмерным пространством, потому что вам мало задать, например, конкретный дом, пусть даже вы зададите его пересечением какой-нибудь «стрит» и какой-нибудь авеню, — вам нужно будет задать еще и этаж, на котором находится нужная вам квартира. Это даст вам третье измерение — высоту. У вас получится трехмерное пространство, в котором каждая точка задается тремя числами.
Вопрос: что такое четырехмерное пространство? Представить его себе не так-то просто, но можно думать о том, что это пространство, в котором каждая точка задается четырьмя числами. На самом деле мы с вами действительно живем в четырехмерном пространстве-времени, потому что события нашей жизни кодируются как раз четырьмя числами — помимо положения в пространстве, есть еще и время. Например, если вы назначаете свидание, то вы можете сделать это так: вы можете указать три числа, которые будут соответствовать точке в пространстве, и обязательно указать время, которое обычно задается в часах, минутах, секундах, но можно было бы закодировать его одним числом. Например, количество секунд, прошедших с определенной даты, — это тоже одно число. Таким образом получается четырехмерное пространство-время.
Представить себе геометрию этого четырехмерного пространства-времени не очень просто. Например, мы с вами привыкли к тому, что в нашем обычном трехмерном пространстве две плоскости могут пересекаться по прямой либо быть параллельными. Но не бывает такого, чтобы две плоскости пересекались в одной точке. Две прямые могут пересечься в одной точке, а на плоскости не могут в трехмерном пространстве. А в четырехмерном пространстве две плоскости могут и чаще всего пересекаются в одной точке. Можно представлять себе, хотя это уже совсем сложно, пространство большей размерности. На самом деле математики, когда работают с пространствами высокой размерности, чаще всего говорят просто: допустим, пятимерное пространство — это пространство, в котором точка задается пятью числами, пятью координатами. Безусловно, математики разработали разные методы, которые позволяют понимать что-то о геометрии такого пространства.
Почему это важно? Зачем понадобились такие пространства? Во-первых, четырехмерное пространство нам важно, потому что оно применяется в физике, потому что мы в нем живем. А зачем нужны пространства более высоких измерений? Давайте представим себе, что мы изучаем какие-то объекты, которые обладают большим количеством параметров. Например, мы изучаем страны, и у каждой страны есть территория, количество населения, внутренний валовой продукт, количество городов, какие-нибудь коэффициенты, индексы, что-нибудь такое. Мы можем представлять себе каждую страну в виде одной точки в каком-то пространстве достаточно высокой размерности. И оказывается, что с математической точки зрения это правильный способ об этом думать.
В частности, переход к геометрии многомерного пространства позволяет анализировать разные сложные объекты, обладающие большим количеством параметров.
Для того чтобы изучать такие объекты, используются методы, разработанные в науке, которая называется линейная алгебра. Несмотря на то, что она алгебра, на самом деле это наука о геометрии многомерных пространств. Конечно, поскольку представить их себе довольно тяжело, математики используют формулы, для того чтобы как раз изучать такие пространства.
Представить себе четырех-, пяти- или шестимерное пространство довольно сложно, но математики не боятся трудностей, и им мало даже стомерных пространств. Математики придумали бесконечномерное пространство — пространство, содержащее бесконечное количество измерений. В качестве примера такого пространства можно привести пространство всех возможных функций, заданных на отрезке или прямой.
Оказывается, что методы, которые были разработаны для конечномерных пространств, во многом переносятся и на случаи чрезвычайно сложных с точки зрения просто попытки их все представить пространств.
У линейной алгебры есть многочисленные приложения не только в математике, но и в самых разных науках, начиная c физики и заканчивая, например, экономикой или политической наукой. В частности, линейная алгебра является основой для многомерной статистики, которая как раз используется для вычленения связей между различными параметрами в каких-то массивах данных. В частности, популярный ныне термин Big Data зачастую связывается с решением задач по обработке данных, которые представляются именно большим количеством точек в пространстве какой-то конечной размерности. Чаще всего такие задачи можно переформулировать и разумно воспринимать именно в геометрических терминах.
Со школьных лет математика разделяется на алгебру и геометрию. Но на самом деле, если мы задумаемся о том, как устроена современная математика, то мы поймем, что те задачи, которые сейчас решаются, в частности, с применением методов линейной алгебры, на самом деле являются очень отдаленным продолжением тех задач, над которыми задумывались многие тысячи лет назад, например Пифагор или Евклид, разрабатывая ту самую школьную геометрию, которая сейчас есть в любом школьном учебнике. Удивительно, что задача по анализу больших данных оказывается в некотором смысле потомком, казалось бы, совсем бессмысленных — по крайней мере с практической точки зрения — упражнений древних греков по рисованию прямых или окружностей на плоскости или мысленному проведению прямых или плоскостей в трехмерном пространстве.
Что такое четырёхмерное пространство («4D»)?
Тессерракт — четырехмерный куб
Всем знакомо сокращение 3D, означающее «трёхмерный» (буква D — от слова dimension — измерение). Например, выбирая в кинотеатре фильм с пометкой 3D, мы точно знаем: для просмотра придётся надеть специальные очки, но зато картинка будет не плоской, а объёмной. А что такое 4D? Существует ли «четырёхмерное пространство» в реальности? И можно ли выйти в «четвёртое измерение»?
Чтобы ответить на эти вопросы, начнём с самого простого геометрического объекта — точки. Точка нульмерна. У неё нет ни длины, ни ширины, ни высоты.
Сдвинем теперь точку по прямой на некоторое расстояние. Допустим, что наша точка — остриё карандаша; когда мы её сдвинули, она прочертила отрезок. У отрезка есть длина, и больше никаких измерений: он одномерен. Отрезок «живёт» на прямой; прямая является одномерным пространством.
Тессеракт — четырехмерный куб
Возьмём теперь отрезок и попробуем его сдвинуть так, как раньше точку. Можно представить себе, что наш отрезок — это основание широкой и очень тонкой кисти. Если мы выйдем за пределы прямой и будем двигаться в перпендикулярном направлении, получится прямоугольник. У прямоугольника есть два измерения — ширина и высота. Прямоугольник лежит в некоторой плоскости. Плоскость — это двумерное пространство (2D), на ней можно ввести двумерную систему координат — каждой точке будет соответствовать пара чисел. (Например, декартова система координат на школьной доске или широта и долгота на географической карте.).
Если сдвинуть прямоугольник в направлении, перпендикулярном плоскости, в которой он лежит, получится «кирпичик» (прямоугольный параллелепипед) — трёхмерный объект, у которого есть длина, ширина и высота; он расположен в трёхмерном пространстве, в таком, в каком живём мы с вами. Поэтому мы хорошо представляем себе, как выглядят трёхмерные объекты. Но если бы мы жили в двумерном пространстве — на плоскости, — нам пришлось бы изрядно напрячь воображение, чтобы представить себе, как можно сдвинуть прямоугольник, чтобы он вышел из той плоскости, в которой мы живём.
Тессеракт — четырехмерный куб
Представить себе четырёхмерное пространство для нас также довольно непросто, хотя очень легко описать математически. Трёхмерное пространство — это пространство, в котором положение точки задаётся тремя числами (например, положение самолёта задаётся долготой, широтой и высотой над уровнем моря). В четырёхмерном же пространстве точке соответствует четвёрка чисел-координат. «Четырёхмерный кирпич» получается сдвигом обычного кирпичика вдоль какого-то направления, не лежащего в нашем трёхмерном пространстве; он имеет четыре измерения.
На самом деле мы сталкиваемся с четырёхмерным пространством ежедневно: например, назначая свидание, мы указываем не только место встречи (его можно задать тройкой чисел), но и время (его можно задавать одним числом, например количеством секунд, прошедших с определенной даты). Если посмотреть на настоящий кирпич, у него есть не только длина, ширина и высота, но ещё и протяженность во времени — от момента создания до момента разрушения.
Физик скажет, что мы живём не просто в пространстве, а в пространстве-времени; математик добавит, что оно четырёхмерно. Так что четвёртое измерение ближе, чем кажется.
Представление других измерений
От 2D к 3D
Ранняя попытка объяснить концепцию дополнительных измерений появилась в 1884 году с публикацией романа о плоской земле Эдвина А. Эббота «Флатландия: романтика множества измерений«. Действие в романе разворачивается в плоском мире, называемом «Флатландия», а повествование ведется от лица жителя этого мира — квадрата. Однажды во сне квадрат оказывается в одномерном мире — Лайнландии, жители которой (треугольники и другие двумерные объекты представлены в виде линий) и пытается объяснить правителю этого мира существование 2-го измерения, однако, приходит к выводу о том, что его невозможно заставить выйти за рамки мышления и представления только прямых линий.
Квадрат описывает его мир как плоскость, населенную линиями, кругами, квадратами, треугольниками и пятиугольниками.
Сфера, с точки зрения Квадрата — Окружность. │ commons.wikimedia.org
Однажды перед квадратом появляется шар, но его суть он не может постичь, так как квадрат в своем мире может видеть только срез сферы, только форму двумерного круга.
Сфера пытается объяснить квадрату устройство трехмерного мира, но квадрат понимает только понятия «вверх/вниз» и «лево/право», он не способен постичь понятия «вперед/назад».
Непостижимая Квадратом тайна третьего измерения на примере прохождения сферы через плоскость. Герой наблюдает уменьшение Окружности до точки и её исчезновение. │ commons.wikimedia.org
Только после того, как сфера вытащит квадрат из его двумерного мира в свой трехмерный мир, он наконец поймет концепцию трех измерений. С этой новой точки зрения квадрат становится способен видеть формы своих соотечественников.
Квадрат, вооруженный своим новым знанием, начинает осознавать возможность существования четвертого измерения. Также он приходит к мысли, что число пространственных измерений не может быть ограничено. Стремясь убедить сферу в этой возможности, квадрат использует ту же логику, что и сфера, аргументирующая существование трех измерений. Но теперь из них двоих становится «близорукой» сфера, которая не может понять этого и не принимает аргументы и доводы квадрата — так же, как большинство из нас «сфер» сегодня не принимают идею дополнительных измерений.
От 3D к 4D
Нам сложно принять эту идею, потому что, когда мы пытаемся представить даже одно дополнительное пространственное измерение — мы упираемся в кирпичную стену понимания. Похоже, что наш разум не может выйти за эти границы.
Представьте себе, например, что вы находитесь в центре пустой сферы. Расстояние между вами и каждой точкой на поверхности сферы равно. Теперь попробуйте двигаться в направлении, которое позволяет вам отойти от всех точек на поверхности сферы, сохраняя при этом равноудаленность. Вы не сможете этого сделать..
Житель Флатландии столкнулся бы с такой же проблемой, если бы он находился в центре круга. В его двумерном мире он не может находиться в центре круга и двигаться в направлении, которое позволяет ему оставаться равноудаленными каждой точке окружности круга, если только он не перейдет в третье измерение. Увы, у нас нет проводника в четырехмерное пространство как в романе Эббота, чтобы показать нам путь к 4D.
Что такое гиперкуб? Построение тессеракта
Виды гиперкубов и их названия
1. Точка — нулевое измерение
2. Отрезок — одномерное пространство
3. Квадрат — двумерное пространство (2D)
4. Куб — трёхмерное пространство (3D)
5. Тессеракт — четырёхмерное пространство (4D)
6. Пентеракт — пятимерное пространство (5D)
7. Хексеракт — шестимерное пространство (6D)
8. Хептеракт — семимерное пространство (7D)
9. Октеракт — восьмимерное пространство (8D)
10. Энтенеракт — девятимерное пространство (9D)
11. Декеракт — десятимерное пространство (10D)
Гиперкуб — это обобщающее название куба в производном числе измерений. Всего измерений десять, плюс точка (нулевое измерение).
Соответственно, существует одиннадцать видов гиперкуба. Рассмотрим построение тессеракта — гиперкуба четвертого измерения:
Для начала построим точку А (рис. 1):
После, соединим ее с точкой В. Получим вектор АВ (рис. 2):
Построим вектор, параллельный вектору АВ, и назовем его CD. Соединив начала и концы векторов, получим квадрат ABDC (рис. 3):
Теперь построим еще один квадрат A1B1D1C1, который лежит в параллельной плоскости. Соединив точки подобным образом, получим куб (рис. 4):
У нас есть куб. Представьте, что положение куба в трехмерном пространстве с течением времени изменилось. Зафиксируем его новое местоположение (рис 5.):
Рис. 5 Измененное положение куба в пространстве
А теперь, мы проводим вектора, которые соединяют местоположение точек в прошлом и в настоящем. Получаем тессеракт (рис. 6):
Рис. 6 Тессеракт (построение)
Подобным образом строятся остальные гиперкубы, конечно же учитывается смысл пространства, в котором гиперкуб находится.
Как насчет 10D?
В 1919 году польский математик Теодор Калуца предположил, что существование четвертого пространственного измерения может увязать между собой общую теорию относительности и электромагнитную теорию. Идея, впоследствии усовершенствованная шведским математиком Оскаром Кляйном, заключалась в том, что пространство состояло как из «расширенных» измерений, так и из «свернутых» измерений. Расширенные измерения — это три пространственных измерения, с которыми мы знакомы, и свернутое измерение находится глубоко в расширенных размерах. Эксперименты позже показали, что свернутое измерение Калуцы и Кляйна не объединило общую теорию относительности и электромагнитную теорию, как это первоначально предполагалось, но спустя десятилетия теоретики теории струн нашли эту идею полезной, даже необходимой.
Математика, используемая в теории суперструн, требует не менее 10 измерений. То есть для уравнений, описывающих теорию суперструн и для того чтобы связать общую теорию относительности с квантовой механикой, для объяснения природы частиц, для объединения сил и т. д. — необходимо использовать дополнительные измерения. Эти измерения, по мнению теоретиков струн, завернуты в свернутое пространство, изначально описанное Калуцей и Кляйном.
Круги представляют собой дополнительный пространственный размер, свернутый в каждую точку нашего знакомого трехмерного пространства. │ WGBH / NOVA
Чтобы расширить скрученное пространство, чтобы включить эти добавленные размеры, представьте, что круги Калуцы-Клейна заменяются сферами. Вместо одного добавленного измерения мы имеем два, если рассматривать только поверхности сфер и три, если учесть пространство внутри сферы. Получилось всего шесть измерений. Так где же другие, которые требует теория суперструн?
Оказывается, что до того, как появилась теория суперструн, два математика Эудженио Калаби из Университета Пенсильвании и Шин-Тунг Яу из Гарвардского университета описали шестимерные геометрические формы. Если мы заменим сферы в скрученном пространстве этими формами Калаби-Яу, мы получим 10 измерений: три пространственных, а также шестимерные фигуры Калаби-Яу.
Шестимерные формы Калаби-Яу могут объяснять дополнительные размеры, требуемые теорией суперструн. │ WGBH / NOVА
Приверженцы теории струн делают ставку на то, что дополнительные измерения действительно существуют. На самом деле, уравнения, описывающие теорию суперструн, предполагают вселенную с не менее чем 10 измерениями. Но даже физикам, которые все время думают о дополнительных пространственных измерениях сложно описать как они могут выглядеть, или как люди могли бы приблизиться к их пониманию.
Если теория суперструн будет доказана и идея мира, состоящего из 10 или более измерений, подтвердится, то появится ли когда-нибудь объяснение или визуальное представление более высоких измерений, которые сможет постичь человеческий разум? Ответ на этот вопрос навсегда может стать отрицательным, если только какая-то четырехмерная жизненная форма не «вытащит» нас из нашего трехмерного мира и не даст нам увидеть мир с ее точки зрения.