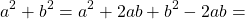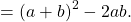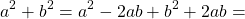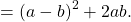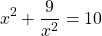что такое сумма квадратов чисел

Сумма квадратов всех целых чисел

Сумма квадратов чисел — математическое выражение, для которого не существует формулы сокращенного умножения. На практике иногда требуется быстро прикинуть сумму нескольких квадратов, однако без математических хитростей такое выражение подсчитать достаточно трудно.

Формулы сокращенного умножения

Для упрощения расчетов в математике используются специальные формулы сокращенного умножения, которые, по сути, представляют собой частные случаи бинома Ньютона. При помощи таких формул легко вручную подсчитать, например, квадрат суммы или разности вида:

(a ± b) 2 = a 2 ± 2ab + b 2

в учебниках по математике вы не найдете. Естественно, она есть для комплексных чисел, тех самых, с которыми мы знакомимся в университетском курсе математического анализа. Выглядит эта формула достаточно жутко:

где i – легендарная мнимая единица, которая рассчитывается как квадратный корень из минус единицы.

В школьных примерах продвинутые ребята негласно используют формулу, которая не входит в пантеон формул сокращенного умножения:

a 2 + b 2 = (a + b) 2 − 2ab.

Эта формула идеально подходит только для вычисления суммы квадратов двух целых чисел. Но что делать, если на практике требуется сложить сумму нескольких квадратов или рациональных чисел? Здесь на сцене появляется наша программа.

Наша программа позволяет сложить сколько угодно квадратов целых и рациональных чисел. Для вычислений вам потребуется ввести числа в ячейку, отделив их пробелом. Десятичные дроби записываются и с точкой, и с запятой. Рациональные числа записываются через / (слэш). Итак, вы можете подсчитать сумму нескольких квадратных чисел, но для чего это вообще нужно?

Рассмотрим примеры работы калькулятора

Разложение на квадраты

Зачем складывать квадраты целых чисел? Почему бы не складывать их кубы или 33-е степени? Эти вопросы встают перед каждым математиком, занимающимся теорией чисел. Разложение целых чисел на сумму двух квадратов — классическая задача теории чисел, за которой стоит исследование делимости. В целом задача эта обратна теме данной статьи: вопрос ставится таким образом, что математик должен вычислить, раскладывается ли данное число на сумму двух квадратов. Некоторые ученые идут дальше и пытаются раскладывать числа на суммы квадратов последовательных чисел. Мы же просто попробуем сложить некоторые квадраты и посмотрим, что получится в результате. Итак, введем в калькулятор следующие пары чисел:

Как видите, разные пары чисел дают один и тот же результат. Кроме того, сами числа 25 и 64 являются квадратами 5 и 8 соответственно. Магия теории чисел, которую трудно применить в каких-нибудь бытовых расчетах.

Гипотенуза 5-мерного тетраэдра

Представим еще менее реальную задачу. Пятимерный тетраэдр или 5-мерный симплекс — это обобщение треугольника для пятимерного пространства. Такие причудливые идеи используются в квантовой физике, теории относительности и барицентрическом исчислении, но для решения некоторых задач от вас не потребуется глубоких знаний высшей математики. К примеру, гипотенуза пятимерного тетраэдра рассчитывается по достаточно простой формуле:

где a, b, c, d – стороны симплекса.

Для решения такой задачки достаточно ввести четыре значения в форму онлайн калькулятора и вычислить квадратный корень из результата. Допустим, стороны симплекса в условных единицах имеют следующие значения: 1, 2.3, 3/5, 0,85. Введем этим данные в ячейку через пробел и получим 7,3725. Теперь вычислим квадратный корень и выясним, что гипотенуза пятимерного симплекса равна 2,715.

Заключение

Сумма квадратов нескольких чисел — нестандартная задача, которая вряд ли встретится в обычных бытовых расчетах, как-то вычисление диаметра дачного ограждения или площади пиццы. Для нетривиальных математических расчетов вам пригодится наша программа, которая быстро вычислит сумму квадратов сколько угодно большого количества целых и рациональных чисел.

Источник

Решение формулы суммы квадратов двух чисел

АННОТАЦИЯ

В настоящей статье нами впервые предложено решение формулы сокращенного произведения, которая может широко применена в решении различных математических задач, равенств и неравенств, а также для упрощения сложных алгебраических выражений, имеющих широкое практическое применение в науке и технике.

ABSTRACT

In this article, we first proposed a solution to the abbreviated product formula, which can be used in solving various mathematical problems, equalities and inequalities, as well as to simplify complex algebraic expressions that have wide practical applications in science and technology.

Ключевые слова: формулы сокращенного произведения, сумма квадратов двух чисел.

Keywords: formulas of short multiplication, sum of squares two numbers.

Известно, что при решении задач во всех разделах математики очень часто используют формулы сокращенного произведения (ФСУ) [1. 163-182, 2. 115, 3. 134]. Эти формулы удачно используются при упрощении сложных математических выражений, при решении алгебраических, тригонометрических уравнений, неравенств, геометрических задач, учебных и научных проблем различной сложности. Ниже приведены официально всем известные ФСУ в табличном виде, из учебников Алгебры для 7 класса:

Таблица 1.

Формулы сокращенного умножения

Формула

Название

(a+b) 2 =a 2 +2ab+b 2

Квадрат суммы двух чисел

Квадрат разности двух чисел

Square of difference

(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3

Куб суммы двух чисел

Куб разности двух чисел

Cube of difference

Сумма кубов двух чисел

Разность кубов двух чисел

Difference of cubes

Разность квадратов двух чисел

Difference of squares

Сумма квадратов двух чисел (Примечание: не разлагающаяся на члены) [8]

Sum of squares (Note: not expands) [8,10]

Наглядно видно из таблицы 1, что приведенные в ней формулы 1, 2; 3, 4; 5, 6; 7, 8 являются формулами-парами, которые отличаются нежели только со знаками у отдельных членов в левой части равенства. Однако, решение для урувнения формулой a 2 +b 2 (8) до настоящего времени ни в официальных источниках, также в учебной и научной литературе не была приведена 2. Тому можно убедиться после ознакомления в электронных интернет учебниках на английском, так и на других языках. В них формула (8) указана как “not expands” – «не разлагающаяся на члены» 10. Также, во всех учебниках для средних образовательных школ по математике, так и в пособиях для ВУЗов Узбекистана, России и Европейских стран, написанные на узбекском, английком, так и на русском языках, формула (8), до настоящего времени обозначается как, “не разлагающаяся на члены”.

В настоящей статье нами впервые предложена конкретное решение для формулы (8), для разложения суммы квадратов двух чисел на многочлены. Она имеет решение следующего вида:

(8)

Доказательство. Результат последовательного произведения многочленов в правой части формулы (8), должны равняться сумме квадратов двух чисел, в левой части равенства. Для этого применяем правила последовательного умножения для многочленов к выражениям в скобках, в правой части равенства:

Примечание. Члены с одинаковыми абсолютными значениями, но с различными знаками взаимно сокращаются, как показано ниже:

;

;

Конец доказательства.

Предложенная нами формула для суммы квадратов двух чисел (8) является инновационной, новой и имеет в дальнейшем практическое применение как в математике, информатике, ИТ, в точных науках в целом, так и в других отраслях науки и техники.

Список литературы

Источник

Сумма квадратов

Сумма квадратов встречается в ходе преобразования числовых и буквенных выражений. Как с ней работать?

Поскольку сумма квадратов является составной частью формул полного квадрата суммы и разности, можно попробовать применить одну из этих формул.

Формула полного квадрата суммы состоит из трёх слагаемых — сумма квадратов двух слагаемых плюс удвоенное произведение этих слагаемых. Следовательно, для получения полного квадрата к сумме квадратов двух выражений следует прибавить удвоенное произведение этих выражений, и, чтобы выражение не изменилось, вычесть это произведение:

Аналогично, для получения полного квадрата разности следует из суммы квадратов двух выражений вычесть удвоенное произведение этих выражений и тут же прибавить его:

Рассмотрим, как эти рассуждения могут быть применены на практике.

Теперь используем данные условия:

Эти рассуждения применяются, например, в приложении теоремы Виета, когда не решая квадратного уравнения, требуется найти сумму квадратов его корней и т.п.

Источник

Модель натурального ряда чисел. Столбцы с суммами квадратов

Модели натурального ряда чисел (НРЧ), рассматриваемые автором в ряде его публикаций, предназначаются для выполнения исследований и установления важных различных свойств НРЧ в целом и отдельного числа в частности. Установленные свойства далее используются при разработке алгоритмов решения конкретных задач, которые назывались здесь и здесь. Основная задача — факторизация большого числа (ЗФБЧ).

В работе сохраняется и используется базовая плоскостная модель НРЧ, обозначаемая символом Г 2± и называемая гиперболо-круговой моделью, что определяется основными соотношениями модели при вычислениях значений в клетках модели (x₁, x₀) выше диагонали Д₀ по формуле окружности N = x 2 ₁+x 2 ₀ и ниже диагонали Д₀ по формуле N = x 2 ₁-x 2 ₀ гиперболы.

Действия с квадратами чисел

В математике существуют упрощенные процедуры и формулы, базирующиеся на простых соотношениях, ускоряющие вычисления. К ним относятся, например, признаки делимости чисел, формулы разложения многочленов на множители, суммы различных рядов и др.

Исследователи в процессе работы часто стремятся свести свою исходную задачу или ее части – подзадачи к известным ускоряющим вычисления соотношениям. Прозорливость и компетентность, а иногда просто везение приводят исследователя к положительным результатам. Но бывают ситуации, когда к упрощающим формулам свести задачу не удается.

Так при суммировании числовых квадратов получаются результаты (числа), которые требуется преобразовать, например, в произведения, но для решения этой задачи таких преобразований отыскать не удается. Проблему несколько проясняют приводимые ниже примеры.

Суммы квадратов и факторизация чисел. В отличие от разности квадратов двух целых
чисел
(х1) 2 – (хо) 2 = (х1– хо) (х1+хо) их сумма (х1) 2 +(хо) 2 не раскладывается столь же простым способом в произведение сомножителей.

Но одно число, представимое суммами двух пар различных квадратов (суммы с одинаковым значением) обладает свойством разложимости числа в произведение. Приведем известный пример Леонарда Эйлера о двух парах квадратов.

Пример 1. (Представление числа суммами двух пар квадратов и его разложение в произведение) Эйлер вначале полагал, что N = 1000009 = 1000 2 + 3 2 – простое число, и ему был известен результат П. Ферма о единственности разложения простого числа N сравнимого с единицей по модулю 4 в сумму квадратов.

Но через несколько лет Эйлер нашел еще одно другое представление числа N суммой квадратов.
N = 1 000 009 = 1000 2 + 3 2 = 972 2 + 235 2 ;
После этого факторизовал его N = 3413∙293 = 1 000 009.

Эйлером предложена схема. Из N = (х1) 2 + d(у1) 2 = (х2) 2 + d(у2) 2 следует, что
(х1) 2 – (х2) 2 = d((у2) 2 – (у1) 2 ) или (х1 – х2) / (y2 – y1) = d (y2 + y1)/ (х1 + х2)

после сокращения дробей получаются целые отличные от нуля числа d, u, v, s, t, (u, v) = 1, такие, что
а) х1 – х2 = dut, б) y2 – y1 = vt,
в) y2 + y1 = us, д) х1 + х2 = vs.

Отсюда, суммируя а) и д), получаем х1 = ½(dut + vs), вычитая из в) равенство б), получим
y1 = ½(us – vt) и N = (х1) 2 + d(у1) 2 = (v 2 + du 2 )(s 2 + dt 2 )/4.

Если d четное, то из нечетности N числа х1 и х2 должны быть нечетными, так что по д) хотя бы одно из чисел v, s четное. Если s (соответственно v) нечетное, то по б, в) u (соответственно t) четное, так как
(y2 – y1), (y2 + y1) имеют одинаковую четность.

Анализ знаков переменных в других случаях оставляю читателям для упражнения. Из рассмотренного следует, что одна из скобок в последнем равенстве кратна четырем и во всех случаях N получает нетривиальное разложение.

Для примера 1 выше получаются значения переменных схемы Эйлера
d = 1, u = 7, v = 58, s = 34, t = 4; и соответственно разложение в произведение двух сумм квадратов. Оба сомножителя — простые числа, сравнимые с 1 по модулю 4.
N = (7 2 + 58 2 )∙(2 2 + 17 2 ) = 3413∙293 = 1 000 009.

Суммы квадратов в чистом виде получаются из схемы Л. Эйлера при d = 1 и такой случай приведен самим Эйлером.Такие ситуации сложно распознаются при произвольном задании числа и оцениваются как достаточно редкие.

Пример 2. Здесь численное значение d равно не единице, а семерке d = 7. Разложение в произведение получается, но в исходной ситуации имеем суммы не чистых квадратов, как это получилось в примере 1 у Эйлера.

N = 13717421 = 761 2 + 7∙1370 2 = 439 2 + 7∙1390 2 ; d = 7, u = 23, v = 10, s = 120, t = 2;
N = (10 2 +7∙23 2 )(60 2 + 7∙1 2 ) = 3803∙3607. Оба сомножителя — простые числа, но сравнимы по модулю 4 не с 1, а с 3, что не позволяет каждое из них представить суммой двух квадратов.

В рассмотренных примерах определенные трудности представляет поиск сумм квадратов для конкретного N. Далее в работе показывается, как в предложенной и рассматриваемой автором плоскостной модели НРЧ с суммами квадратов решается задача факторизации.

Использование свойств и привлечение закономерностей НРЧ в теоретико-числовых исследованиях, работа с моделями НРЧ показали, что на самом деле практически все составные нечетные числа, во-первых, представимы двумя или более парами квадратов, дающих совпадающие суммы значений и, во-вторых, всегда при этом коэффициент d =1, что делает процедуру факторизации более просто реализуемой.

Описание базовой плоскостной Г 2± – модели натурального ряда чисел (НРЧ)

Тем читателям, которые стремятся вникнуть в содержание работы, автор рекомендует с карандашом в руках проследить все рассматриваемые действия, что удобно делать с контролем элементов из рисунка 1, который желательно иметь перед собой (распечатать) для удобства чтения.

Модель в работе ограничена начальным фрагментом, она используется только для получения математических зависимостей, проверки и подтверждения их истинности.

Базовая Г 2± – модель представляет собой дискретную плоскость в форме бесконечного квадрата из клеток (x₁, x₀), где x₁ — номер строки, x₀ — номер столбца. Все клетки уникальны.

В плоскости введена прямоугольная система координат x₁0x₀, начало которой в левом верхнем углу экрана (листа), в точке (0,0). Ось х1 направлена вниз, ось х0 — вправо от начала координат.

Длинная диагональ Д1= образована клетками с координатами
(х1, хо) = (х1, х1–1), содержащими все нечетные числа d1 от 1 до бесконечности, включая и нечетные простые числа.

Значения в клетках длинной диагонали Д₁ + = <d₁ + > устроены иначе. В ее клетках с координатами (х1, хо) = (х1, х1+1), содержатся значения суммы квадратов координат.

Факторизация с использованием смежных столбцов Г 2 + – модели НРЧ

Свойства элементов диагонали Д1 весьма примечательны и полезны во многих отношениях.
Например, положение нечетного числа d1 в некоторой клетке при разложении его в сумму двух смежных чисел-слагаемых, обеспечивает распознавание простоты этого числа.

Слагаемые в такой сумме интерпретируются как номера столбцов Г 2± –модели. Если клетки смежных столбцов не содержат ни одной пары одинаковых значений чисел, то представляемое суммой число d1 простое. Высказанное утверждение иллюстрируется числовым примером 4.

Свойства Г 2 + – модели

Наблюдения и работа с базовой моделью позволили сформулировать и высказать ряд утверждений о свойствах Г 2 + – модели, связанных с суммами квадратов чисел, образующих столбцы Г 2 + – модели.

Утверждение 2. Для любого СННЧ N(x₁, x₀)є Д₁ столбцы Г 2 + – модели с номерами хо1 =х1 и хо2=хо1 +1 содержат одну или более пар клеток с совпадающими для каждой пары своими значениями.

Наличие таких пар клеток с совпадающими числами обеспечивает выполнение факторизации СННЧ N(x₁, x₀).

Важное свойство диагонали Д1 состоит в том, что наличии двух или более пар клеток с совпадающими значениями в разных смежных столбцах это указывает на то, что d1є Д₁ составное число и создают возможность факторизации составного числа d1 элементарными (быстро выполняемыми) действиями.

Это легко показывается с привлечением модели НРЧ. Обозначим смежные номера столбцов через хо2–1 и хо2, номера строк х12 и х11, содержащих клетки (х12, хо2), (х11, хо2-1) на пересечении со столбцами, а также совпадающие числа в этих клетках символами
N (х12, хо2) = N (х11, хо2-1).

Таким образом, наличие пары совпадающих чисел в смежных столбцах модели обеспечивает мультипликативное представление числа d1 = 2хо2-1, что является при простых сомножителях по существу его факторизацией.

Высказанные утверждения о свойствах иллюстрируются числовыми примерами.

Пример 3. (Факторизация составного числа)
Задано число СННЧ d1 = N(x₁, x₀) = 87. Оно лежит в клетке длинной диагонали Д₁ под главной диагональю модели.

Над этой клеткой в строке с номером х1=43 отметим два столбца с номерами хо1=43 и хо2=44. Представление числа N = 87 суммой двух смежных чисел 87 = 43 + 44 соответствует таким номерам столбцов.

Анализ содержимого клеток этих двух столбцов в областях над главной диагональю модели свидетельствует, что в столбцах имеются числа:
N (х11 = 16, хо1 = 43) = 2105 в клетке с координатами (х11 = 16, хо1 = 43) и
N (х12 = 13, хо2 = 44) = 2105 в клетке с координатами (х12= 13, хо2 = 44), которые совпадают своими значениями.

Обе эти клетки и их координаты можно пометить на рисунке Г 2 + – модели НРЧ. Далее действуем по алгоритму:
а) Запишем для пары клеток с равными значениями чисел базовые соотношения Г 2 + – модели
N (х11, хо1) = (х11) 2 + (хо1) 2 =16 2 + 43 2 = 2105 и
N (х12, хо2) = (х12) 2 + (хо2) 2 =13 2 + 44 2 = 2105;

б) приравняем их средние части (х11) 2 + (хо1) 2 = (х12) 2 + (хо2) 2 ;
в) преобразуем суммы в разности квадратов одноименных координат
(х11) 2 — (х12) 2 = (хо2) 2 — (хо1) 2 ;

г) подставим числовые значения координат 16 2 — 13 2 = 44 2 — 43 2 и преобразуем разности квадратов в произведения:
(16 — 13)(16 + 13) = (44 — 43 )(44 + 43) или 3·29 = 1·87. Из этого следует, что число
N =87=3·29 успешно факторизовано.

Обозначим смежные номера столбцов через хо2 — 1 и хо2, номера строк х11 и х12, содержащих клетки (х11, хо2 — 1) и (х12, хо2) на пересечении со столбцами, а также совпадающие числа в этих клетках символами N(х11, хо2 — 1) = N(х12, хо2).

По основному соотношению модели значения чисел в клетках представляются как функции координат клеток, в которых они помещаются
N(х11, хо2 — 1) =(х11) 2 +(хо2 — 1) 2 и N(х12, хо2) =(х12) 2 +(хо2) 2

Такое свойство указанных столбцов Г 2 + – модели следует рассматривать как новый признак простоты числа N. Следующий пример иллюстрирует справедливость утверждения 3.

Пример 4. (Установление простоты числа)
а) Задано число СННЧ d1 = N(x₁, x₀) = 83. Оно лежит в клетке длинной диагонали Д₁ под главной диагональю модели.

Над этой клеткой в строке с номером х1=42 отметим два столбца с номерами хо2=42 и хо1=41. Представление числа N = 83 суммой двух смежных чисел 83 = 41 + 42 соответствует таким номерам столбцов.

Анализ содержимого клеток этих двух столбцов над главной диагональю модели свидетельствует, что чисел N (х12, хо2 = 42) и N (х11, хо1 = 41) с совпадающими значениями в этих столбцах нет. Из чего следует, что число d1 = 83 не удается представит произведением нетривиальных сомножителей, и, возможно, оно простое, а d1 = 87 – составное, что выше и было показано.

Утверждение 4. Пары клеток двух смежных столбцов с одинаковым удалением верхней клетки от нижней с совпадающими значениями чисел в них принадлежат двум параллельным линиям (бесконечным лучам) Г 2 + – модели НРЧ.

Все верхние клетки образуют верхний луч, а нижние клетки – параллельный верхнему нижний луч и при этом пары смежных столбцов с клетками, формирующими лучи, следуют с шагом, равным удаленности клеток (нечетное число d1)

Пример 5. (Смежные столбцы содержат более одной пары клеток с совпадающими значениями чисел)
Задано число СННЧ d1 = N(x₁, x₀) = 63.

Анализ содержимого клеток этих двух столбцов в областях над главной диагональю модели свидетельствует, что в столбцах имеются числа:
N (х11 = 8, хо1 = 31) = 1025 в клетке с координатами (х11 = 8, хо1 = 31) и
N (х12 = 1, хо2 = 32) = 1025 в клетке с координатами (х12= 1, хо2 = 32), которые совпадают своими значениями.

Обе эти клетки и их координаты можно пометить на рисунке Г 2 + – модели НРЧ. Далее действуем по алгоритму:

а) Запишем для пары клеток с равными значениями чисел базовые соотношения Г 2 + – модели
(х12) 2 + (хо –1) 2 = (х11) 2 + (хо) 2 = 8 2 + 31 2 = 1025 и,
(х12) 2 – (х11) 2 = (хо) 2 – (хо – 1) 2 =1 2 +32 2 = 1025.

Это еще не все. Оказывается пара анализируемых столбцов содержит еще клетки с совпадающими значениями
N (х11 = 12, хо1 = 31) = 12 2 + 31 2 = 1105 в клетке с координатами
(х11 =12, хо1 = 31) и N (х12 = 1, хо2 = 32) = 9 2 +32 2 =1105 в клетке с координатами (х12=1, хо2=32). Устанавливаем номера х11 =12, х12 = 9 строк для клеток с совпадающими в них значениями 1105.

После этого вычисляем значение для левой части соотношения
(х11 — х12)(х11 + х12) =(12 — 9)(12 + 9) = 3·21 =63. Найдены другие факторы числа
3·21 =63. Обобщение приведенных фактов приводит к выявлению определенной структуры параллельных линий в НРЧ.

Структура пар параллельных линий в Г 2 + – модели. Примерами иллюстрируется возможность факторизации отдельного числа при использовании смежных столбцов Г 2 + – модели.

На самом деле модель предоставляет более широкие возможности, так как содержит систему нумерованных параллельных линий L, L = 1(1)∞, или факторизующую числа N структуру линий и клеток в них, обеспечивающую при определенных условиях быструю факторизацию всех составных нечетных чисел.

Утверждение 4. Пары клеток Г 2 ∓ – модели с одинаковым удалением верхней от нижней с совпадающими значениями чисел в них двух смежных столбцов принадлежат двум параллельным прямым линиям (бесконечным лучам) Г 2 ∓ – модели.

Все верхние клетки пар образуют верхний луч, а нижние – нижний луч параллельный верхнему. При этом пары смежных столбцов с клетками, формирующими лучи, следуют с шагом, равным удаленности клеток (нечетным числам d1).

При рассмотрении рисунка 1, его верхней половины, обратим внимание на несколько отклоняющиеся от горизонтального направления пары параллельных линий, начинающихся с различным отступом от левого края плоскости с сеткой.

Значение отступа определяется парами клеток с совпадающими числовыми значениями в смежных столбцах, причем, нижняя из двух параллельных линий начинается в клетке столбца с номером на единицу меньшим, чем номер столбца клетки начала верхней линии.

Эти клетки соединены отрезками прямых линий. Для каждой пары параллельных линий отрезки изображаются с регулярностью в виде «ступеней лестниц», боковинами которых как раз являются параллельные линии. Внимательное рассмотрение приводит к выводу о том, что все ступени соединяют пары клеток с равными числовыми значениями клеток верхней и нижней боковин лестниц.

Лестницы смещены вправо очередная относительно предшествующих и частично накрывает их. Лестницы нумеруются, введением обозначения номера лестницы L = 1(1)∞,. Аналогично нумеруются символом s = 0(1)∞ ступени каждой лестницы.

Желательно установить закон, определяющий эту не совсем понятно, как и почему возникающую «лестничную структуру», хотя детерминированность исходной плоскости с сеткой клеток с числами представляется достаточно простой и прозрачной для понимания.

Начнем анализ структуры с описания первых длинных диагоналей модели и с (s = 0) нулевых ступенек лестниц. Рассмотрим подробнее строение длинных диагоналей
Д₁ + = < d₁ + > и Д1 = , где d₁ + и d1 — обозначения чисел в клетках соответствующих диагоналей и самих клеток в них.

Это диагонали смежные с главной диагональю сверху нее и снизу. Координаты клеток этих диагоналей — смежные числа и различаются на 1. Они образованы клетками
(х1, хо) = (х1, х1 + 1), так как х1 + и (х1, хо) = (х1, х1 — 1), так как х1 > хо для Д1.

В клетках первых диагоналей размещаются соответственно числовые значения d₁ + и d1, зависящие от координат клеток.

Для диагонали Д₁ из основного соотношения следует d1(х1, хо) = 2х0–1. Множество чисел в клетках – это все непрерывно возрастающие от единицы нечетные числа. Начальный фрагмент чисел этой диагонали получает вид d1(х1, хо) = <1, 3, 5, 7, 9, 11, …>.

Разность координат клетки х1 – (х1 – 1) = 1 – это номер длинной, т. е. первой диагонали.
Сумма координат клеток равна х1 + хо = а – номеру короткой диагонали Кi, проходящей через клетки обеих длинных диагоналей.

Именно эта короткая диагональ объединяет клетки двух первых длинных диагоналей в пары значений, порождающих нулевые ступени и сами лестницы.

_{Кликабельно}
Рисунок 1 — Факторизация в Г 2 ∓ – модели. Пары параллельных линий, содержащие клетки с совпадающими значениями в смежных столбцах

Начальный фрагмент чисел диагонали Д₁ + принимает вид d₁ + (х1, хо) = <1, 5, 13, 25, 41, 61,…>. Аналогично начальный фрагмент чисел диагонали Д1(х1, хо) = <1, 3, 5, 7, 9, 11,…>. Из этих фрагментов формируются пары чисел (1,1),(3,5),(5, 13),(7,25),(9, 41), (11,61). которые используются при построении системы факторизации.

Пара клеток с (1, 1) не используется для формирования лестничной структуры, а все остальные пары из коротких диагоналей порождают начальные (s = 0) ступени своих лестниц и сами лестницы.

С другой стороны, значения N(х1, хо) = d1(х1, хо) используются и рассматриваются как сумма номеров соответствующих столбцов. Столбцы с этими номерами содержат пары клеток из параллельных линий в Г 2+ (рис.1).

Эти линии своим началом имеют как раз пары клеток смежных столбцов (нулевая ступенька) с совпадающими значениями равными квадратам значений
(d₁ + (х1, хо)) 2 из клеток коротких диагоналей.

Параллелограм. Две пары смежных столбцов с номерами х01 = 40, х02 = 41 и х03 = 49,
х04 = 50 имеют 4 клетки, например, N(0, 41) = N(9, 40) и N(10, 49) = N(1, 50) на пересечении с горизонталями х11 = 0, х12 = 9, х13 = 1, х14 = 10, разнесенными в лестнице на фиксированное число (d1 = 9) строк и столбцов.

Клетки для различных пар линий оказываются в вершинах увеличивающихся в размерах параллелограммов, которые последовательно смещаются вниз (на одну строку) и вправо для каждой пары линий (на соответствующее ей число: 3, 5, 7, 9, 11, 13, …) столбцов.

Квадраты этих чисел (d₁ + (х1, хо)) 2 помещаются в верхних клетках столбцов модели с большим номером. Номера смежных столбцов хо2 и (хо2 – 1), Г 2+ модели НРЧ в сумме равны нечетному составному числу d1 = хо2 + хо2 –1 = (2хо2 – 1)є Д1.

Локализация позиции N и поиска совпадений. Таким образом, задавая значение числа d1є Д1 и представляя его суммой смежных чисел, указываются номера смежных столбцов модели. Значения в клетках столбца уникальны.
Для таких столбцов выполняется анализ содержимого клеток на совпадение значений.

Пример 6. (начальные значения в верхних клетках нулевых ступеней лестниц
L = 1(1)5) Рассмотрим формирование значений в клетках диагонали Д₁ + :
d₁ + (х1, хо) = d₁ + (0,1)=0 2 +1 2 = 1;
d₁ + (х1, хо) = d₁ + (1,2)=1 2 +2 2 = 5;
d₁ + (х1, хо) = d₁ + (2,3)=2 2 +3 2 =13;
d₁ + (х1, хо) = d₁ + (3,4)=3 2 +4 2 = 25;
d₁ + (х1, хо) = d₁ + (4,5)=4 2 +5 2 = 41;
d₁ + (х1, хо) = d₁ + (5,6)=5 2 +6 2 = 61;…

Для клетки d₁ + (х1, хо) = х1 2 + хо 2 = 0 2 +1 2 =1; лестница вырождена и не формируется.

Координаты клетки Д₁ + со значениями х1 = 5, хо = 6, например, d₁ + (5, 6) = 61є Д₁ + всегда последовательные числа.Возникающая лестница получает номер L = х1 = 5.

Таблица 1–Характеристики начальных клеток 0-й ступени лестничной структуры

Факторизующая структура в координатной плоскости.
Эта структура представлена бесконечным множеством нумерованных пар параллельных (верхняя и нижняя) линий L, L = 1(1)∞, с постоянным расстоянием h(L) = 2L+1 (своим для каждой пары линий) между ними.

На каждой из параллельных линий пары регулярно размещаются образующие ступени (х1i, хоi) точки (клетки верхняя и нижняя)
N (х1в, хов) = (х1в) 2 + (хов) 2 = (х1н) 2 + (хон) 2 = N (х1н, хон)
с совпадающими значениями, которые для наглядности как ступеньку лестницы соединяем отрезками прямых линий.

Четыре точки, образованные последовательными парами равных значений (ступенями), можно рассматривать как вершины параллелограммов. Эти параллелограммы на каждой паре параллельных линий создают некую «лестницу» с бесконечным числом ступеней фиксированной высоты h(L), зависящей от номера лестницы.

Ступени s каждой «L-лестницы» имеют одинаковую нумерацию s = 0, 1, 2, 3, … ∞. Каждая пара линий L направлена под разными углами к горизонтальной координатной оси и проходит через точки с совпадающими значениями сумм квадратов координат (целых чисел).

Структура пар параллельных линий (лестниц) в Г 2 + – модели НРЧ подобна лестницам со ступенями, соединяющими пары клеток (боковин лестницы) с совпадающими значениями.

Примеры 3, 5 иллюстрируют возможность факторизации отдельного нечетного числа N = d1. Это число задается произвольно, но раз оно нечетное, то всегда содержится в клетке диагонали Д1.

Далее число d1 = хо2 + хо1 представляется суммой смежных чисел, в которых слагаемые задают номера столбцов для дальнейшего анализа наличия в них клеток с совпадающими значениями. Если такие клетки найдены, то для них определяются номера содержащих их строк.

Лестничная структура определяет положение клеток с равными значениями в крайних клетках-«ступеней».
Делителями заданного числа N будут сумма и разность номеров строк с найденными клетками
N = d1 = (х11 + хо1) (х11 – хо1).

Приведем описание такой структуры. Структура образована в верхней полуплоскости Г 2 + – модели НРЧ множеством пар параллельных линий (лучей) бесконечной длины.

Верхняя линия в каждой паре линий начинается в клетке нулевой строки
(х1 = 0), содержащей квадраты номеров столбцов, и в столбцах с номерами, равными каждому из чисел d_1j + с порядковым номером j = 1, 2.

Эти две клетки – вершины левой стороны параллелограмма и начальные точки пары параллельных линий. Две другие вершины параллелограмма смещены каждая на одну строку вниз (относительно первых вершин) и вправо на d1j (шаг) столбцов, где d1j = 3, 5, 7, 9, 11, …. Направление линий совпадает с верхней и нижней сторонами параллелограмма.

Пример 7. (Вычисления 8 ступенек через вершины с совпадающими значениями для конкретной «лестницы»). Пусть номер «лестницы» L= 3. Построим ее начальный фрагмент, содержащий ступени с номерами s = 0(1)7.

Координаты верхней клетки нулевой ступени х1 =0, х02 = d₁ + = 25. Высота ступеней и ширина «лестницы» h (L = 3) = 2L +1 = 7, начало нулевой ступени (верхняя линия пары) – вершина (клетка) лежит на координатной оси в точке (х1= 0, хо + s ∙h(3)) = (0, 25).

Значение в верхней (Bi) вершине-клетке (х1 = 0, хо = 25),
N (х1, хо) = N (0, 25 + s ∙h(3)) = 0 2 +25 2 = 625.
Нижняя клетка (Нi) ступени в точке (х1 = h(3), хо = хо –1+ s∙h(3)) = (7, 24+0∙7) = (7, 24).

Значение числа в этой клетке N (7, 24) = 7 2 + 24 2 = 625. Совпадающие значения в клетках очередных ступеней s = 2, 3, 4, …, 7 сведены в таблицу 2.

Таблица 2 – Клетки первых 8 ступеней и значений в клетках L=3-ей «лестницы», хо= 25

Разности между значениями N нарастают от 400 на 100 единиц с каждой новой ступенькой. Описание лестничной структуры и пример фрагмента «лестницы» обеспечивают представление каждого составного нечетного натурального числа N произведением двух сомножителей.

Образ «лестницы» используется для наглядности структуры и ясности в понимании логики решения задачи факторизации больших чисел (ЗФБЧ).

Пример 8. (Фрагменты числового представления трех «лестниц» структуры).
Рассмотрим начальные фрагменты трех (при j = 1, 2, 3) «лестничных конструкций» структуры. Выбираем значения d_1j + = 5, 13, 25, а d_1j = 3, 5, 7.

Нижние линии параллельных пар начинаются клетками в строках с номерами (х1 = 3, 5, 7 в столбцах с номерами меньшими на единицу, хо = 4, 12, 24) и значениями в них, совпадающими со значениями первых верхних клеток, т. е. N (3, 4) = 25, N(5, 12) =169, N(7, 24) = 625.
Очередные клетки нижних линий в строках с номерами на единицу большими (х1 = 4, 6, 8, а номера столбцов на единицу меньшими хо = 7, 17, 31) при совпадающих значениях
N(4, 7) = 65, N(6, 17) = 325, N(8, 31) = 1025.

Таблица 3 – Фрагменты 3-х лестниц структуры, содержащие по 8 ступеней

В колонках таблицы приведены значения в клетках Г 2 + – модели НРЧ, принадлежащих верхней и нижней линиям (боковинам лестниц с номерами L = 1, 2, 3). Левая колонка – номера ступеней s = 0(1)7. При факторизации чисел большую роль играют смежные числа, суммы и разности их квадратов.

Таблица 4– Характеристики факторизующей структуры «лестничного типа»

Логика алгоритма решения ЗФБЧ

В таблице 4 характеристик факторизующей структуры в строке разности (это разности квадратов смежных чисел) представлены все простые и СННЧ. Выбор любого числа N в этой строке задается разностью квадратов смежных чисел из верхней строки таблицы структуры, т. е. N = хо1 + хо2, где хо1 = хо2 – 1. Далее определяется номер L= хо1 лестницы и номер s ступени на ней.

Предполагая, что хо2 соответствует верхней точке s-й ступени и принадлежит верхней линии пары, определяем начальную точку линии как один из полных квадратов, меньший значения хо2. Первым квадратом выбирается ближний к хо2, и в строке таблицы 4 выше выбирается номер L.

В таблице такой квадрат помещен в строке суммы, что соответствует сумме квадратов другой пары смежных чисел. Вычисляется разность хо2 – d1j+, которая затем делится на высоту h(L) ступени.

Если частное – целое число, то переходим к определению значений в вершинах параллелограммов, после чего определяются координаты х1в и х1н вершин.
Определенные значения позволяют вычислить делители N.

Пример 9. (Использование лестничной структуры и столбцов Г 2 + – модели).
Задано СННЧ N = 119. Представляем его суммой смежных чисел N = хо1 + хо2 = 59 + 60.

Эти числа – номера столбцов Г 2 + – модели, с другой стороны, они рассматриваются как вторые координаты крайних клеток ступени с некоторым целым номером s, принадлежащей L-й лестнице.

Вначале определяем, какой ступеньке s и какой по номеру L из лестниц соответствует заданное число N. Зная шаг ступени каждой из лестниц, координату начальной (верхней) клетки их нулевой по номеру ступени можно вычислить при целом s (номере ступени),
s = ∆L/h(L), где ∆L – удаленность номера столбца (60) от начала лестницы с номером L,
h(L) – высота ступени L-й лестницы.

Для этого сопоставляем номера (60 – вторая координата клетки верхнего края ступени, 59 – нижнего края) столбцов разложения заданного числа N = 119 = 59 +60 и числа в клетках начальных (нулевых,
s = 0) ступеней лестниц, номера которых меньше 60.

Находим разности ∆4(L = 4) = 60 – 41 = 19 и ∆3(L =3) = 60 – 25 = 35 и частные
s = ∆4/ h(L) = 19/9 = 2, 1(1) не целое s = ∆3/h(L) = 35/7 = 5 – целое число, равное номеру s = 5 ступени «лестницы» с номером L= 3.

Для определенных номеров лестницы и ступени на ней находим первые координаты х1в и х1н крайних (верхней и нижней) точек 3 ступени: х1в = s = 5 и х1н = s + h(L= 3)=5 +7 =12.

Определяем делители СННЧ N: dм = (х1н – х1в) = 12 – 5 = 7 и dб = (х1в + х1н) = 5 +12 = 17. Найдены простые делители, что завершает факторизацию числа N = 119 = 7·17.

Возвращаясь к примерам 1 и 2 воспользуемся рассмотренной в работе Г 2 + – моделью и лестничной структурой.
Число Эйлера, принадлежащее длинной диагонали Д1 представим суммой смежных номеров столбцов N = 1000009 = 500004 +500004.

Разность 1853 2 – 1560 2 = (1853 +1560)( 1853 –1560) = 3413·293= 1000009 квадратов этих номеров раскладывается в произведение сомножителей равное исходному числу, которое факторизовано здесь другим методом.

Другое число (пример 2) N=13717421 = 6858710 + 6858711 также принадлежит длинной диагонали Д1 и представляется суммой смежных номеров столбцов над клеткой с этим N.

Разность 3705 2 – 98 2 = (3705 + 98)( 3705 – 98) = 3803·3607 = 13717421 квадратов этих номеров раскладывается в произведение сомножителей равное исходному числу, которое здесь факторизовано другим методом.

Можно предположить, что во времена Ферма и Эйлера отсутствие компьютеров не позволяло формировать громоздкие модели из числовых данных и исследовать их. Они шли своим путем и многого сумели достичь без таких моделей, но их подходы не могут быть использованы сегодня для разработки алгоритмов и решения задачи факторизации больших чисел в современных условиях.

Мировая практика вычислений как раз и свидетельствует об этом. В то время им не удалось решить задачи о распределения делителей в натуральном ряде ни задачи перечисления и распределения простых чисел. В настоящее время процесс поиска решений таких задач стал весьма актуальным, и мы медленно, но верно приближаемся к его завершению.

Другой подход к поиску равных (совпадающих) значений в клетках с использованием смежных столбцов Г 2 + – модели.

Задано СННЧ N = 119. К этому числу необходимо подобрать такой полный квадрат (□), сумма числа с которым окажется большим полным квадратом. Очевидно, подбираемый квадрат не будет сильно отличаться от√119=10.

Выполним перебор вариантов:
119 +1 = 120 ≠ ▢; 119 + 4 =123 ≠ ▢; 119 + 9 = 128 ≠ ▢; 119 +16 = 135 ≠ ▢; 119 + 25 = 144 = ▢. Символ ▢ обозначает, что результат — полный квадрат.
На пятом шаге нашелся нужный квадрат, равный 25.

Тогда, добавляя найденные квадраты к квадратам смежных чисел разложения 119 = 59 + 60 в сумму, получаем равные значения в клетках смежных столбцов:
59 2 +12 2 =3481+ 144 = 3625; 60 2 + 5 2 =3625.

Дальше действуем по шаблону и находим делители N = 119
Запишем для клеток с равными значениями чисел базовые соотношения Г 2 + – модели:

а) N (х11, хо1) = (х11) 2 + (х01) 2 = 59 2 +12 2 =3481+ 144 = 3625; и
N (х12, хо2) = (х12) 2 + (х02) 2 = 60 2 + 5 2 = 3625.

б) приравняем их средние части:
(х11) 2 + (х01) 2 = (х12) 2 + (х02) 2 ;

в) преобразуем суммы в разности квадратов одноименных координат:
(х11) 2 – (х12) 2 = (х02) 2 – (х01) 2 ;

г) подставим числовые значения 12 2 – 5 2 = 60 2 – 59 2 и преобразуем разности в произведения:
(12 – 5) · (12 + 5) = (60 – 59)·(60 + 59) или 7·17 = 1·119, откуда число N = 119 = 7·17 успешно факторизовано.

Для решения задачи необходимо подготовить исходные данные, т. е. два смежных столбца с суммами квадратов. При наличии таких столбцов необходимо определить в их составе клетки, содержащие одинаковые значения. Пока эти задачи решаются только непосредственными вычислениями.

Процесс формирование столбцов можно совместить с поиском пары клеток, содержащих совпадающие значения в них.
А Л Г О Р И Т М решения задачи факторизации составного нечетного натурального числа
1. Задаются число N и вычисляются номера столбцов хо1 = 44 и хо2 = 43;
2. В цикле по i = 0(1)I, I = хо2 – предельное значение размера столбца, вычисляются суммы квадратов
(хi1) 2 + (хо1) 2 для первого столбца и
(хi2) 2 + (хо2) 2 для второго столбца
3. вычисленные суммы правого столбца сравниваются с суммами левого; как только сумма левого превысит значение в клетке правого, то это значение меняется на очередное большее;
4. сравнения сумм квадратов продолжается до совпадения, либо до исчерпания значения I.

Источник