что такое структурирование данных
Основные структуры данных. Матчасть. Азы
Все чаще замечаю, что современным самоучкам очень не хватает матчасти. Все знают языки, но мало основы, такие как типы данных или алгоритмы. Немного про типы данных.
Еще в далеком 1976 швейцарский ученый Никлаус Вирт написал книгу Алгоритмы + структуры данных = программы.
40+ лет спустя это уравнение все еще верно. И если вы самоучка и надолго в программировании пробегитесь по статье, можно по диагонали. Можно код кофе.
В статье так же будут вопросы, которое вы можете услышать на интервью.
Что такое структура данных?
Структура данных — это контейнер, который хранит данные в определенном макете. Этот «макет» позволяет структуре данных быть эффективной в некоторых операциях и неэффективной в других.
Какие бывают?
Линейные, элементы образуют последовательность или линейный список, обход узлов линеен. Примеры: Массивы. Связанный список, стеки и очереди.
Нелинейные, если обход узлов нелинейный, а данные не последовательны. Пример: граф и деревья.
Основные структуры данных.
Массивы
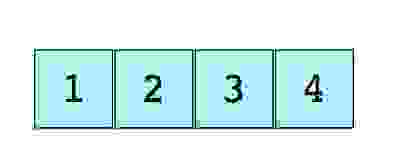
Массив — это самая простая и широко используемая структура данных. Другие структуры данных, такие как стеки и очереди, являются производными от массивов.
Изображение простого массива размера 4, содержащего элементы (1, 2, 3 и 4).
Каждому элементу данных присваивается положительное числовое значение (индекс), который соответствует позиции элемента в массиве. Большинство языков определяют начальный индекс массива как 0.
Бывают
Одномерные, как показано выше.
Многомерные, массивы внутри массивов.
Основные операции
Вопросы
Стеки
Стек — абстрактный тип данных, представляющий собой список элементов, организованных по принципу LIFO (англ. last in — first out, «последним пришёл — первым вышел»).
Это не массивы. Это очередь. Придумал Алан Тюринг.
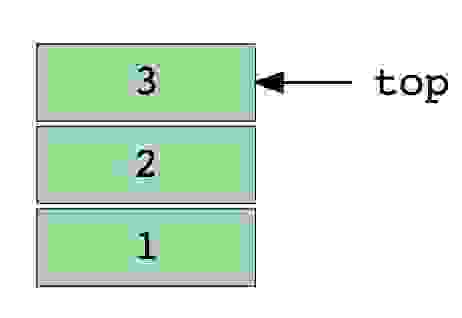
Примером стека может быть куча книг, расположенных в вертикальном порядке. Для того, чтобы получить книгу, которая где-то посередине, вам нужно будет удалить все книги, размещенные на ней. Так работает метод LIFO (Last In First Out). Функция «Отменить» в приложениях работает по LIFO.
Изображение стека, в три элемента (1, 2 и 3), где 3 находится наверху и будет удален первым.
Основные операции
Вопросы
Очереди
Подобно стекам, очередь — хранит элемент последовательным образом. Существенное отличие от стека – использование FIFO (First in First Out) вместо LIFO.
Пример очереди – очередь людей. Последний занял последним и будешь, а первый первым ее и покинет.
Изображение очереди, в четыре элемента (1, 2, 3 и 4), где 1 находится наверху и будет удален первым
Основные операции
Вопросы
Связанный список
Связанный список – массив где каждый элемент является отдельным объектом и состоит из двух элементов – данных и ссылки на следующий узел.
Принципиальным преимуществом перед массивом является структурная гибкость: порядок элементов связного списка может не совпадать с порядком расположения элементов данных в памяти компьютера, а порядок обхода списка всегда явно задаётся его внутренними связями.
Бывают
Однонаправленный, каждый узел хранит адрес или ссылку на следующий узел в списке и последний узел имеет следующий адрес или ссылку как NULL.
Двунаправленный, две ссылки, связанные с каждым узлом, одним из опорных пунктов на следующий узел и один к предыдущему узлу.
Круговой, все узлы соединяются, образуя круг. В конце нет NULL. Циклический связанный список может быть одно-или двукратным циклическим связанным списком.
Самое частое, линейный однонаправленный список. Пример – файловая система.
Основные операции
Вопросы
Графы
Граф-это набор узлов (вершин), которые соединены друг с другом в виде сети ребрами (дугами).
Бывают
Ориентированный, ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами.
Неориентированные, к каждому из ребер можно осуществлять переход в обоих направлениях.
Смешанные
Встречаются в таких формах как
Общие алгоритмы обхода графа
Вопросы
Деревья
Дерево-это иерархическая структура данных, состоящая из узлов (вершин) и ребер (дуг). Деревья по сути связанные графы без циклов.
Древовидные структуры везде и всюду. Дерево скилов в играх знают все.
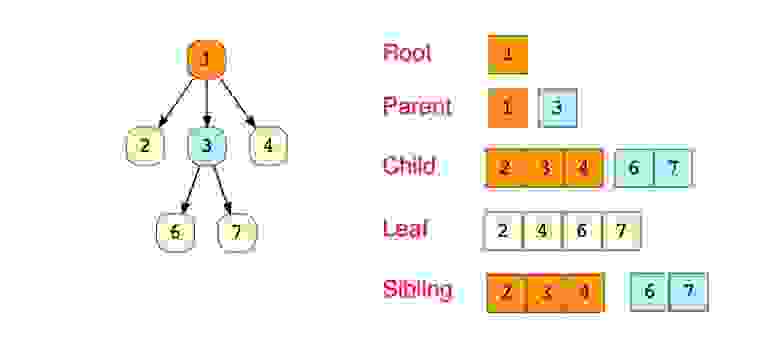
«Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. » — Procs
Три способа обхода дерева
Вопросы
Trie ( префиксное деревое )
Разновидность дерева для строк, быстрый поиск. Словари. Т9.
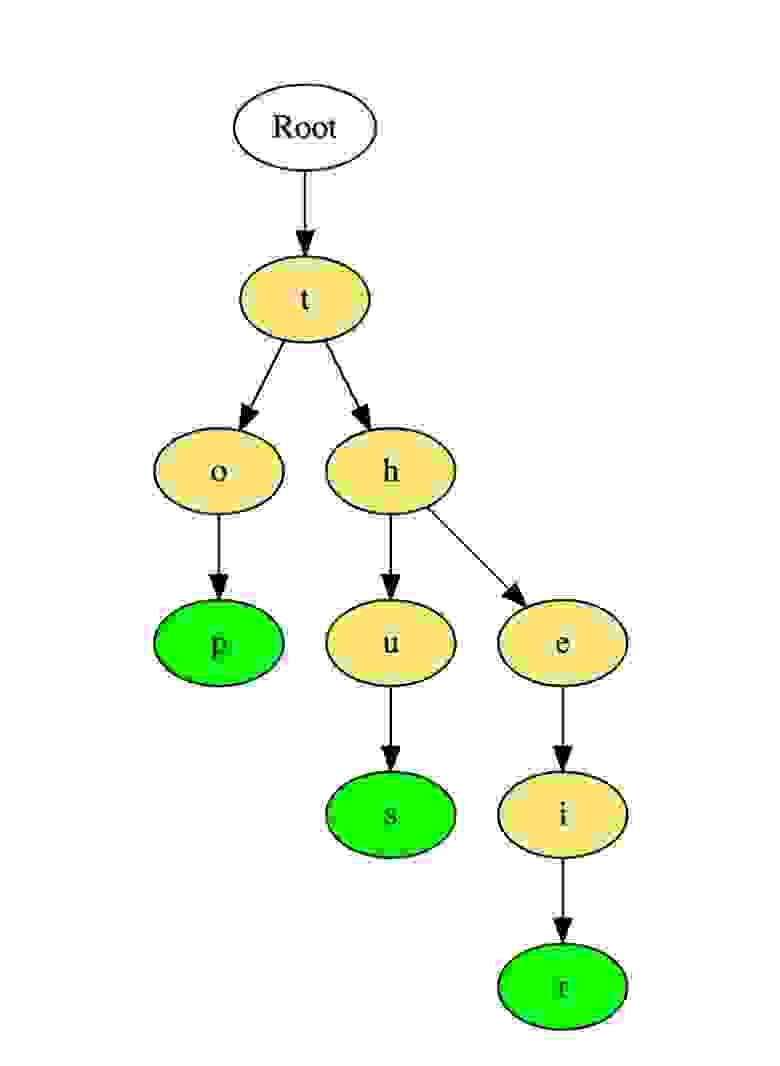
Вот как такое дерево хранит слова «top», «thus» и «their».
Слова хранятся сверху вниз, зеленые цветные узлы «p», «s» и «r» указывают на конец «top», «thus « и «their» соответственно.
Вопросы
Хэш таблицы
Хэширование — это процесс, используемый для уникальной идентификации объектов и хранения каждого объекта в заранее рассчитанном уникальном индексе (ключе).
Объект хранится в виде пары «ключ-значение», а коллекция таких элементов называется «словарем». Каждый объект можно найти с помощью этого ключа.
По сути это массив, в котором ключ представлен в виде хеш-функции.
Эффективность хеширования зависит от
Вопросы
Список ресурсов
Вместо заключения
Матчасть так же интересна, как и сами языки. Возможно, кто-то увидит знакомые ему базовые структуры и заинтересуется.
Спасибо, что прочли. Надеюсь не зря потратили время =)
PS: Прошу извинить, как оказалось, перевод статьи уже был тут и очень недавно, я проглядел.
Если интересно, вот она, спасибо Hokum, буду внимательнее.
О выборе структур данных для начинающих
Часть 1. Линейные структуры
Массив
Когда вам нужен один объект, вы создаёте один объект. Когда нужно несколько объектов, тогда есть несколько вариантов на выбор. Я видел, как многие новички в коде пишут что-то типа такого:
Это даёт нам значение пяти рекордов. Этот способ неплохо работает, пока вам не потребуется пятьдесят или сто объектов. Вместо создания отдельных объектов можно использовать массив.
Будет создан буфер из 5 элементов, вот такой:
Заметьте, что индекс массива начинается с нуля. Если в массиве пять элементов, то они будут иметь индексы от нуля до четырёх.
Недостатки простого массива
Если вам нужно неизменное количество объектов, то массив вполне подходит. Но, допустим, вам нужно добавить в массив ещё один элемент. В простом массиве этого сделать невозможно. Допустим, вам нужно удалить элемент из массива. В простом массиве это так же невозможно. Вы привязаны к одному количеству элементов. Нам нужен массив, размер которого можно менять. Поэтому нам лучше выбрать…
Динамический массив
Динамический массив — это массив, который может менять свой размер. Основные языки программирования в своих стандартных библиотеках поддерживают динамические массивы. В C++ это vector. В Java это ArrayList. В C# это List. Все они являются динамическими массивами. В своей сути динамический массив — это простой массив, однако имеющий ещё два дополнительных блока данных. В них хранятся действительный размер простого массива и объём данных, который может на самом деле храниться в простом массиве. Динамический массив может выглядеть примерно так:
Элемент internalArray указывает на динамически размещаемый буфер. Действительный массив буфера хранится в maxCapacity. Количество использовуемых элементов задаётся currentLength.
Свой инструмент нужно знать в лицо: обзор наиболее часто используемых структур данных
Некоторое время назад я сходил на собеседование в одну довольно большую и уважаемую компанию. Собеседование прошло хорошо и понравилось как мне, так и, надеюсь, людям его проводившим. Но на следующий день, в процессе разбора полетов, я обнаружил, что в ходе собеседования ответ на как минимум один вопрос был неверен.
Вопрос: Почему поиск в python dict на больших объемах данных быстрее чем итерация по индексированному массиву?
Ответ: В dict хранятся хэши от ключей. Каждый раз, когда мы ищем в dict значение по ключу, мы сначала вычисляем его хэш, а потом (внезапно), выполняем бинарный поиск. Таким образом, сложность составляет O(lg(N))!
На самом деле никакого бинарного поиска тут нет. И сложность алгоритма не O(lg(N)), а Amort. O(1) — так как в основе dict питона лежит структура под названием Hash Table.
Причиной неверного ответа было то, что я не удосужился досконально изучить те структуры, которые лежат в основе работы с коллекциями моего любимого языка. Правда, по результатам опроса нескольких знакомых разработчиков, оказалось что это не только моя проблема, очень многие вообще не задумываются, как работают коллекции в их любимых ЯП. А ведь используем мы их каждый день и не по разу. Так родилась идея этой статьи.
1. Array — он же индексированный массив.
Array — это коллекция фиксированного размера, состоящая из элементов одинакового типа.
Почему время доступа к элементу по индексу постоянно? Массив состоит из элементов одного типа, имеет фиксированный размер и располагается в непрерывной области памяти => чтобы получить j-й элемент массива, нам достаточно взять указатель на начало массива и прибавить к нему размер элемента умноженный на его индекс. Результат этого несложного вычисления будет указывать как раз на искомый элемент массива.
*aj = beginPointer + elementSize*j-1
Примеры:
с/с++: int i_array[10];
java/C#: int[10] i_array;
Python: array.array
php: SplFixedArray
2. List (список).
List — это список элементов произвольного типа переменной длины (то есть мы можем в любой момент добавить элемент в список или удалить его). Список позволяет перебирать элементы, получать элементы по индексу, а так же добавлять и удалять элементы. Реализации у List возможны разные, основные — это (Single/Bidirectional) Linked List и Vector. Классический List предоставляет возможность работы с ним напрямую и через итератор, интерфейсы обоих классов рассмотрим ниже.
Перейдем к реализациям списка.
2.1 Single Linked List

Однонаправленный связный список (односвязный список) представляет из себя цепочку контейнеров. Каждый контейнер содержит внутри себя ссылку на элемент и ссылку на следующий контейнер, таким образом, мы всегда можем переместиться по односвязному списку вперед и всегда можем получить значение текущего элемента. Контейнеры могут располагаться в памяти как им угодно => добавление в односвязный список нового элемента тривиально.
Bidirectional Linked List мы подробно рассматривать не будем, вся разница между ним и Single Linked List заключается в том, что в контейнерах есть ссылка не только на следующий, но и на предыдущий контейнер, что позволяет перемещаться по списку не только вперед, но и назад.
2.2 Vector
Vector — это реализация List через расширение индексированного массива.
Очевидно, что главное преимущество Vector’а — быстрый доступ к элементам по индексу, унаследовано им от обычного индексированного массива. Итерировать Vector так же достаточно просто, достаточно увеличивать некий счетчик на единицу и осуществлять доступ по индексу. Но за скорость доступа к элементам приходиться платить временем их добавления. Для того чтобы вставить элемент в середину Vector’a (insert-after) необходимо скопировать все элементы между текущим положением итератора и концом массива, как следствие время доступа в среднем O(N). То же и с удалением элемента в середине массива, и с добавлением элемента в начало массива. Добавление элемента в конец массива при этом может быть выполнено за O(1), но может и не быть — если опять таки потребуется копирование массива в новый, потому говорится, что добавление элемента в конец Vector’а происходит за Amort. O(1).
Примеры:
с/с++: std::vector
Java: java.util.ArrayList
C#: System.Collections.ArrayList, System.Collections.List
Python: list
3. Ассоциативный массив(Словарь/Map)
Коллекция пар ключ=>значение. Элементы (значения) могут быть любого типа, ключи обычно только строки/целые числа, но в некоторых реализация диапазон объектов, которые могут быть использованы в качестве ключа, может быть шире. Размер ассоциативного массива можно изменять путем добавления/удаления элементов.
3.1 Hash Table

Как можно догадаться из названия, тут используются хэши. Механика работы Hash Table следующая: в основе лежит все тот же индексированный массив, в котором индексом работает значение хэша от ключа, а значением — ссылка на объект, содержащий ключ и хранимый элемент (bucket). При добавлении элемента — хэш функция вычисляет хэш от ключа и сохраняет ссылку на добавляемый элемент в ячейку массива с соответствующим индексом. Для получения доступа к элементу мы опять таки берем хэш от ключа и, работая так же как с обычным массивом получаем ссылку на элемент.
То есть, кроме значения ключа, она так же получает текущий размер массива, это необходимо для определения длины хэша: если мы храним всего 3 элемента — нет смысла делать хэш длиной в 32 разряда. Обратная сторона такого поведения хэш функции — возможность коллизий. Коллизии на самом деле характерны для Hash Table, и существует два метода их разрешения:
Chaining: 
Каждая ячейка массива H является указателем на связный список (цепочку) пар ключ-значение, соответствующих одному и тому же хеш-значению ключа. Коллизии просто приводят к тому, что появляются цепочки длиной более одного элемента.
В массиве H хранятся сами пары ключ-значение. Алгоритм вставки элемента проверяет ячейки массива H в некотором порядке до тех пор, пока не будет найдена первая свободная ячейка, в которую и будет записан новый элемент. Этот порядок вычисляется на лету, что позволяет сэкономить на памяти для указателей, требующихся в хеш-таблицах с цепочками.
Примеры:
c++: за исключением QHash автору не известныboost::unordered_map/boost::unordered_set (by NickLion)
java: java.util.HashMap
c#: System.Collections.Hashtable, System.Collections.Dictionary
python: dict
php: array()
3.2 Binary Tree

На самом деле не просто Binary Tree, а Self-balancing Binary Tree. Причем следует отметить, что существует несколько различных деревьев, которые могут быть использованы для реализации Ассоциативного массива: red-black tree, AVL-tree и т.д. Мы не будем рассматривать каждое из этих деревьев в деталях, так как это возможно тема еще одной, отдельной статьи, а может и нескольких (если изучать деревья особо тщательно). Опишем только общие принципы.
Определение: двоичное дерево — древовидная структура данных в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками. В случае, если у узла нет наследников — он называется листовым узлом.
4. Множество (Set).
Immutable набор элементов. Множество определяется один раз — при создании, и в дальнейшем предоставляет доступ к элементам только на чтение. Множество нельзя расширить, равно как нельзя и удалить из него элементы или изменить элемент множества. В качестве базы для реализации данной коллекции обычно используется Hash Table — описание которого см. Выше.
Множество — это просто реализация абстракции математического множества, т.е. набора уникальных различимых элементов. (спс. danilI)
Примеры:
c++: std::set
java: java.util.Set
C#: System.Collections.HashSet
python: set/frozenset
Сравнительные характеристики структур данных:
Структуры данных в различных языках программирования:
Ссылки:
Так же автор заглянул в исходники PHP и почитал доку по STL.
Upd. Да, в питоне есть обычный индексированный массив (array.array). Спасибо enchantner. С поправкой, тип не обязательно числовой, тип можно указывать.
Upd.
Из комментариев zibada:
Да, вот как раз из-за отсутствия описания итерации по Map из статьи вообще непонятно, зачем, казалось бы, нужны деревья, когда есть хэши. (O(logN) против O(1)).
Нужны они затем, что перечислять элементы Map (или Set) можно хотеть:
— в любом, негарантированном порядке (HashMap, встроенные хэши в некоторых скриптовых языках);
— в порядке добавления (LinkedHashMap, встроенные хэши в некоторых других скриптовых языках);
— в порядке возрастания ключей + возможность перебрать только ключи в заданном диапазоне.
А вот для последнего случая альтернатива деревьям — только полная сортировка всей коллекции после каждого изменения или перед запросом.
Что долго и печально для больших коллекций, но вполне работает для небольших — поэтому в скриптовые языки деревья особо и не встраивают.
Структуры данных: список, который умеет всё*
* Под всё имеется в виду относительно быстрое выполнение операций над единичным элементом массива.
Структур данных, которые реализуют список полно. У всех есть свои достоинства и недостатки. Например в мире Java — в зависимости от необходимых операций — можно использовать:
Возможно, кто-то догадался, что можно взять TreeList, который умеет быстро вставлять/удалять элементы в середине списка и добавить к нему HashMap из объекта в индекс в TreeList для быстрого выполнения indexOf(obj). И это будет простое, изящное, но неверное решение. Ведь при добавлении в середину или удалении из середины нужно будет пересчитать индексы, в среднем, для половины элементов. Это ухудшит производительность до O(n).
Дальше я расскажу о структуре данных, которая может всё из перечисленного выше. Которая выполняет любую операцию над одним элементом за O(log(n)) времени. Ну почти — за логарифм выполняется в том случае, когда все объекты в списке различны. Если в списке есть одинаковые объекты, то возможно проседание производительности вплоть до O(log(n) ^ 2).
Предупрежу сразу, что я не буду здесь расписывать код. Он может быть достаточно сложен для статьи. Но он есть, написан на Java. За основу взят класс TreeList из apache common-collections. Pull request уже есть, но на момент написания статьи ещё не влит.
Также я не буду описывать общеизвестные алгоритмы. Например, алгоритмы балансировки дерева. Большинству может быть достаточно принять на веру тот факт, что дерево можно держать сбалансированным. На понимание общей идеи это никак не влияет. Те, кто захотят узнать больше, без проблем найдут информацию. Но о некоторых базовых вещах очень коротко расскажу, т. к. без знания основ нельзя будет понять многие ключевые элементы.
Ссылки будут в конце.
Зачем это нужно
В самом деле, не так-то просто придумать ситуации, когда от списка нужно вот прям вообще всё. Вряд ли это какая-то супер необходимая структура, иначе о ней знали бы все. Однако несколько примеров, где такой список мог быть полезен можно привести.
Я осознаю, что многие из примеров надуманные. Всё или почти всё можно решить другим способом.
Кэширование и сжатие
Моя первоначальная задача, из-за которой я начал исследовать вопрос. Игрался со сжатием специфических данных и понадобился список для кэша объектов.
Идея следующая: при обработке очередного объекта ищем его в списке. Если не нашли — сохраняем объект и добавляем его в начало списка. Если нашли, то берём его индекс в списке и вместо объекта сохраняем только его индекс, после чего перемещаем объект в начало списка. Таким образом, объекты, которые встречаются часто будут получать маленькие индексы, а объекты, которые встретились всего один раз, со временем перемещаются в конец списка и удаляются.
Очередь
Если вместо обычной FIFO очереди для каких-то задач использовать подобную структуру, то можно делать следующие операции:
Таблица рекордов
Допустим, мы хотим хранить время, за которое игроки проходят уровень в какой-то игре. Игроков много и все они соревнуются, пытаясь показать минимальное время. Данные игроков можно положить в массив и отсортировать по времени. Пользуясь данной структурой можно:
Структура данных
Структура основана на дереве с неявным ключом. Именно на этом подходе основан, например, TreeList в apache common-collections. Для того чтобы двигаться дальше, надо понять как работает эта структура.
Дерево с неявным ключом
Дерево состоит из узлов (Nodes). Каждый узел содержит ссылку на объект, который хранится в узле и 2 ссылки на другие узлы: левый и правый. Самый верхний узел называется корневым. В самом простом случае узел выглядит примерно так:
В классическом бинарном дереве для каждого узла в левом поддереве все объекты меньшие, чем в текущем узле, а в правом — большие. Например:
Но для нашей цели такое дерево не подходит. Нам не надо хранить объекты отсортированными, но надо иметь к ним доступ по индексу, как в массиве.
Как можно поместить массив в дерево? Давайте выберем элемент с индексом i из середины массива. Поместим в корневой узел i-й элемент из массива. Из корневого узла выходят 2 поддерева. В левое поддерево помещаем половину массива с индексом i. Как это сделать? Точно так же: выбираем в подмассиве какой-то элемент из середины, помещаем этот элемент в узел, получаем еще 2 подмассива поменьше. И так пока не поместим все элементы массива в узлы дерева.
Например, так может выглядеть массив с элементами [“q”, “w”, “e”, “r”, “t”, “y”, “u”]:
Средний элемент в массиве “r”, его помещаем в корневой узел. Два подмассива [“q”, “w”, “e”] и [“t”, “y”, “u”] помещаются в левое и правое поддерево. Для этого из подмассивов выбираются центральные элементы, в нашем случае это “w” и “y”, они и попадают в узлы следующего уровня. И т. д.
В нашем случае дерево сбалансировано, глубина всех поддеревьев одинаковая. Но это не обязательно должно быть так.
На картинке выше каждый узел помимо элемента и ссылок на левый и правые узлы содержит количество элементов всего поддерева. Эту информацию надо правильно обновлять при изменении дерева.
Давайте посмотрим, как в таком дереве найти, например, элемент с index = 4.
Мы начинаем обход с корневого узла (root, в нашем случае с элементом “r”). У нас есть 3 варианта: мы уже находимся на нужном узле, нужный узел слева, нужный узел справа. Для того чтобы понять, где искать нужный элемент, нужно сравнить размер левого поддерева (в нашем случае left.size = 3) и текущий индекс (в нашем случае 4). Если эти 2 числа равны, то мы нашли необходимый узел и искомый элемент в нём. Если размер левого поддерева больше, то необходимый узел в левом поддереве. Если меньше, то надо искать в правом поддереве, но нужно уменьшить искомый индекс: index = index — left.size — 1.
Поскольку в нашем случае left.size 0 то ищем в левом поддереве, перемещаемся к узлу с элементом “t”.
В этом узле нет левого поддерева, и его размер равен 0. index = left.size, а значит мы нашли узел с индексом 4 и можем достать из него искомый элемент “t”.
В псевдокоде это выглядит примерно так:
Я постарался описать ключевой принцип как поместить массив в дерево. Работает такая структура, конечно, медленнее классического массива, за O(log(n)) против O(1). Но у неё есть важное преимущество: добавление элемента в середину или удаление из середины работает тоже за O(log(n)) против O(n) у массива. Конечно, при условии, что дерево более-менее сбалансировано. Существует много алгоритмов поддержания дерева в почти сбалансированном виде. Например, красно-чёрное дерево, AVL дерево, Декартово дерево. Я не буду расписывать подробности балансировки дерева, для нас подойдёт любой алгоритм. Давайте просто считать, что дерево в среднем сбалансировано и его максимальная глубина не сильно отличается от минимальной.
Небольшая оптимизация
Подход описанный выше, с проверкой размера дерева слева удобен для восприятия, но можно сделать чуть более эффективно. Для того, чтобы не заглядывать каждый раз в левое поддерево можно вместо размера дерева хранить в узле его позицию относительно позиции его узла-родителя. Корневой узел хранит абсолютную позицию, которая совпадает с размером левого поддерева.
Эта оптимизация помимо более быстрого поиска элемента в списке даст более быстрый и простой поиск индекса у узла. Но, конечно, правильно обновлять позицию при изменении дерева стало чуть сложнее.
Добавляем индексирование
Итак, в дереве мы умеем брать элемент по индексу, менять его значение, добавлять элементы в середину и удалять. По сути, нам осталось добавить быстрый поиск индекса по значению, indexOf(obj). Тогда contains(obj) и remove(obj) будут решаться тривиально.
Но для начала давайте немного упростим задачу. Давайте сделаем структуру, которая хранит только уникальные элементы.
Для того чтобы что-то быстро искать обычно используют таблицу. В мире Java таблицы называются Map, у неё есть 2 основные реализации: HashMap и TreeMap. Ключом таблицы будет ссылка на объект, а значением ссылка на его узел:
Т.е. структура состоит из двух частей: само дерево-список и таблица со ссылками на объекты и узлы этого дерева. При обновлении дерева надо обновлять и таблицу. Детально расписывать процесс не буду. Интуитивно он должен быть понятен: добавили узел — положили его же в таблицу, удалили узел — удалили из таблицы. На практике же есть нюансы с балансировкой дерева: алгоритм должен менять ссылки между узлами, а не перемещать объекты между узлами. Иначе придётся делать много обновлений в таблице и упадёт производительность.
Ок, будем считать, что мы умеем быстро находить узел по элементу, который в нём содержится. И что? Нам нужно найти его индекс, а сделать этого пока нельзя. Но мы можем усложнить класс узла так, чтобы он содержал не только ссылки на левый и правый узлы, но и на своего родителя:
Конечно, обновление дерева ещё немного усложняется, ведь нам теперь нужно аккуратно обновлять ссылку на родителя. Зато теперь, зная узел, мы можем пройти по дереву вверх и вычислить индекс любого узла. Если мы использовали оптимизацию из предыдущей главы, то нам надо просто посчитать сумму позиций от текущего узла до корневого.
Для списка, содержащего уникальные элементы задачу можно считать решенной.
Правда, у нас появилась небольшая проблемка. Допустим, мы вызываем set(index, obj). Мы можем легко заменить один элемент в узле на другой, но только в том случае, если нового элемента в списке еще нет. А если есть, то что делать? Удалить лишний элемент из старой позиции и положить в новую? Или наоборот, сначала добавить, а потом удалить? Результат может быть разным. А можно вообще ничего не делать или бросать исключение. Идеального решения нет.
Отсортировать стандартными методами такой список тоже, скорее всего, не получится. Ведь алгоритм сортировки не будет знать про необходимость уникальности объектов и при перемещении элементов в списке будет создавать дубликаты.
Убираем уникальность
Ок, усложняем ещё, разрешим хранить одинаковые объекты. Очевидно, что надо что-то делать с таблицей. Первая идея хранить в ней список узлов кажется не очень хорошей: с увеличением длины списка будет ухудшаться производительность. Вплоть до O(n), если все элементы списка будут одинаковыми.
Тогда давайте попробуем хранить в таблице вместо списка отсортированное дерево узлов. Отсортированное по позиции в списке.
Тогда вставка/удаление в/из TreeSet размера m будет происходить за log(m) сравнений позиций узлов, а каждое сравнение будет происходить за log(n) времени. Итоговая сложность вставки или удаления в подобную структуру будет происходить за O(log(n) * (1 + log(m))), где n это общее количество элементов в списке, а m это количество элементов в списке равных вставляемому/удаляемому. В худшем случае, когда все элементы равны друг другу, получим сложность O(log(n) ^ 2).
Внимательный читатель наверняка возразит: а как же иммутабельность? Мы ведь не можем изменять объекты, если они являются ключами таблицы? В общем случае так и есть. Однако для дерева, которое хранит в ключах отсортированные объекты, помимо стандартных правил для сравнений, достаточно сохранять инвариант: если a Код под спойлером
Для начала я сравнил скорость доставания случайного элемента из списка. Предупрежу сразу, что в данном тесте накладные расходы очень существенны. Результаты, приближающиеся к 100000 * 1000 операций в секунду сильно искажены.
Тут, как ни странно, самый большой интерес вызывает стандартный ArrayList. Теоретически скорость доставания из него должна быть константой и не зависеть от количество элементов. На практике производительность сначала держится около 90000 * 1000 операций в секунду (помним про накладные расходы), но при длине списка в несколько тысяч элементов начинает проседать. Виной тому всё более частый cache miss: в кэше процессора не оказывается нужных данных и нужно всё чаще ходить за данными в оперативную память. При миллионе элементов скорость прохождения теста ниже в 10 раз, но на практике проседание производительности еще больше.
TreeList, IndexedTreeList и IndexedTreeListSet ожидаемо показывают схожий результат. Ожидаемо сильно медленнее, чем ArrayList. Даже при маленьком количестве элементов TreeList в несколько раз медленнее, чем ArrayList, хотя тест показывает разницу всего в 2 раза.
Следующий тест addRemoveRandom. Здесь в каждом тесте я вставляю в случайную позицию элемент и удаляю из случайной позиции элемент.
Можно было предположить, что ArrayList работает быстрее на маленьких списках. Однако то, что он выигрывает в этом тесте на списках вплоть до 10000 элементов выглядит интересно. Видимо, System.arrayCopy очень хорошо оптимизирован и использует все возможности современных процессоров. Начиная с 10000 элементов специализированные структуры данных начинают выигрывать. При 1000000 элементов разница скорости в 30-50 раз.
IndexedTreeList и IndexedTreeListSet ожидаемо медленнее, чем TreeList. Примерно в 1.5 — 2 раза.
Оставшиеся 2 теста indexOfKnown и indexOfUnknown как раз должны продемонстрировать основную особенность данной структуры. Различие тестов в том, что в одном случае мы ищем элемент, который есть в списке, а в другом случае ищем элемент, которого в списке нет.
Здесь у ArrayList и TreeList почти без сюрпризов. С увеличением размера скорость падает практически линейно. Поиск элемента не из списка ожидаемо в 2 раза медленнее, чем поиск элемента из списка, т.к. надо пройти весь массив вместо половины в среднем.
А вот IndexedTreeList и IndexedTreeListSet здесь показывают ожидаемо хороший результат. Эти структуры данных показывают сравнимую с ArrayList скорость выполнения indexOf даже при 10 элементах. При 1000 элементах эти структуры быстрее в 10 раз, при 1000000 быстрее в 1000 раз. При поиске элемента, которого нет в списке они ожидаемо дают лучшую скорость, чем при поиске элемента из списка.
На что еще интересно обратить внимание, так это на проседание производительности у IndexedTreeList и IndexedTreeListSet в тесте indexOfUnknown. Тут ситуация аналогичная той, что была в тесте с ArrayList.get. Теоретически мы не должны были получить падение производительности, а на практике, из-за cache miss получили, причём существенно.
Вместо заключения
Я до сих пор не знаю, есть ли в предложенной структуре новизна или нет. С одной стороны, идея не сложная, если знать как работает дерево по неявному ключу. С другой стороны, описания структуры со такими свойствами я не встречал. А раз так, то есть смысл сделать структуру более известной, возможно, кому-то пригодится.
Но даже если это ещё один велосипед, то я постарался сделать его полезным. Pull request в common-collections создан, но на момент написания статьи ещё не влит. Зная, как медленно всё может происходить в open source, не удивлюсь, если процесс затянется на месяцы.
Несколько удивил результат сравнения производительности ArrayList и TreeList. Тесты показали, что TreeList нет смысла использовать на размерах списка до 10000 элементов. Было бы интересно попробовать b-tree вместо бинарного дерева. Эта структура должна более бережно использовать память и, скорее всего, быстрее работать. И под неё можно адаптировать идею с индексированием.
В любом случае, прикольно иметь в арсенале инструмент, который может (почти) всё с предсказуемой сложностью.