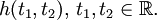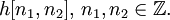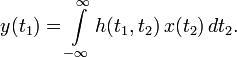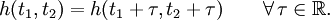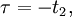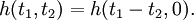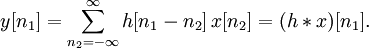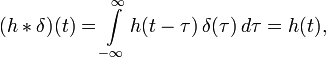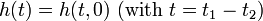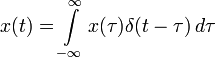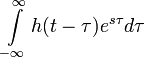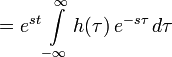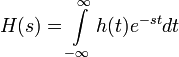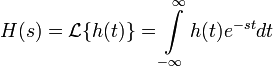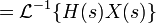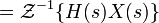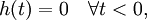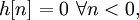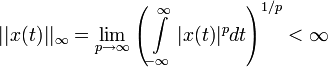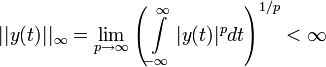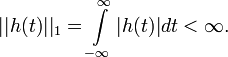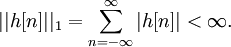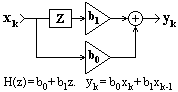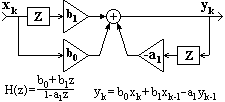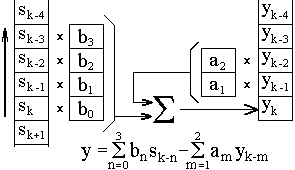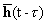Классификация физических систем

Про­ве­дём клас­си­фи­ка­цию фи­зи­че­ских си­стем на ос­но­ве су­ще­ствен­ных свойств их ма­те­ма­ти­че­ских мо­де­лей.

Ста­ци­о­нар­ные и не­ста­ци­о­нар­ные си­сте­мы

Си­сте­ма на­зы­ва­ет­ся ста­ци­о­нар­ной, ес­ли её вы­ход­ная ре­ак­ция не за­ви­сит от то­го, в ка­кой мо­мент вре­ме­ни по­сту­па­ет сиг­нал, т. е.

Ста­ци­о­нар­ная си­сте­ма на­зы­ва­ет­ся так­же си­сте­мой с по­сто­ян­ны­ми па­ра­мет­ра­ми. Ес­ли же свой­ства си­сте­мы не ин­ва­ри­ант­ны от­но­си­тель­но на­ча­ла от­счё­та вре­ме­ни, то та­кую си­сте­му на­зы­ва­ют не­ста­ци­о­нар­ной (си­сте­мой с пе­ре­мен­ны­ми па­ра­мет­ра­ми, или па­ра­мет­ри­че­ской си­сте­мой).

Ли­ней­ные и не­ли­ней­ные си­сте­мы

Си­сте­ма на­зы­ва­ет­ся ли­ней­ной, ес­ли в ней вы­пол­ня­ет­ся прин­цип су­пер­по­зи­ции, ма­те­ма­ти­че­ски за­пи­сы­ва­е­мый в ви­де сле­ду­ю­щих ра­венств:

Ес­ли эти усло­вия не вы­пол­ня­ют­ся, то си­сте­ма яв­ля­ет­ся не­ли­ней­ной. Стро­го го­во­ря, все фи­зи­че­ские си­сте­мы, ис­поль­зу­е­мые в из­ме­ри­тель­ной тех­ни­ке, в той или иной сте­пе­ни не­ли­ней­ны. Од­на­ко су­ще­ству­ет мно­го си­стем, ко­то­рые весь­ма точ­но опи­сы­ва­ют­ся ли­ней­ны­ми мо­де­ля­ми. Так, прак­ти­че­ски все­гда мож­но пре­не­бречь не­ли­ней­но­стью обыч­ных ре­зи­сто­ров, кон­ден­са­то­ров, не­ко­то­рых ин­дук­тив­ных эле­мен­тов, вхо­дя­щих в со­став из­ме­ри­тель­ных це­пей.

Из прин­ци­па су­пер­по­зи­ции и из усло­вия ста­ци­о­нар­но­сти вы­те­ка­ет важ­ное след­ствие — гар­мо­ни­че­ский сиг­нал, про­хо­дя че­рез ли­ней­ную ста­ци­о­нар­ную си­сте­му, со­хра­ня­ет свою фор­му, при­об­ре­тая лишь дру­гие ам­пли­ту­ду и на­чаль­ную фа­зу.

Со­сре­до­то­чен­ные и рас­пре­де­лён­ные си­сте­мы

Кри­те­ри­ем этой клас­си­фи­ка­ции яв­ля­ет­ся со­от­но­ше­ние фи­зи­че­ских раз­ме­ров эле­мен­тов си­сте­мы l и ра­бо­чей дли­ны вол­ны λ ге­не­ри­ру­е­мых или транс­ли­ру­е­мых сиг­на­лов. Ес­ли ха­рак­тер­ный раз­мер си­сте­мы l ≪ λ, то си­сте­ма от­но­сит­ся к клас­су со­сре­до­то­чен­ных. Свой­ства со­сре­до­то­чен­ных си­стем сла­бо за­ви­сят от кон­фи­гу­ра­ции со­еди­ни­тель­ных про­вод­ни­ков, по­это­му для их опи­са­ния ис­поль­зу­ют так на­зы­ва­е­мые прин­ци­пи­аль­ные схе­мы. Так, в ра­дио­тех­ни­ке со­сре­до­то­чен­ные си­сте­мы ши­ро­ко при­ме­ня­ют до ра­бо­чих ча­стот в не­сколь­ко со­тен МГц. Лишь при ча­сто­тах свы­ше ты­ся­чи МГц (СВЧ-диа­па­зон) на сме­ну со­сре­до­то­чен­ным си­сте­мам при­хо­дят си­сте­мы с рас­пре­де­лён­ны­ми па­ра­мет­ра­ми. Их рас­чёт со­став­ля­ет со­дер­жа­ние от­дель­ных ра­дио­тех­ни­че­ских дис­ци­плин.

Источник

Стационарная система

69. Стационарная система

Система, в которой сдвиг входного сигнала во времени приводит к такому же сдвигу выходного сигнала

Смотри также родственные термины:

3.18 Стационарная система пенного пожаротушения (неавтоматическая): Включает резервуары для воды и пенообразователя, насосную станцию и сеть растворопроводов с пожарными гидрантами. Средства автоматизации этих систем должны обеспечить включение резервных насосов в случае, если основные неисправны или не обеспечивают расчетный напор.

Полезное

Смотреть что такое «Стационарная система» в других словарях:

стационарная система — stacionarioji sistema statusas T sritis automatika atitikmenys: angl. time invariant system vok. zeitinvariantes System, n rus. стационарная система, f pranc. système stationnaire, m … Automatikos terminų žodynas

Стационарная система пенного пожаротушения (неавтоматическая) — 3.18 Стационарная система пенного пожаротушения (неавтоматическая): Включает резервуары для воды и пенообразователя, насосную станцию и сеть растворопроводов с пожарными гидрантами. Средства автоматизации этих систем должны обеспечить включение… … Словарь-справочник терминов нормативно-технической документации

Стационарная система связи — часть системы управления, построенная на базе стационарных узлов и линий связи … Пограничный словарь

Линейная стационарная система — Теория линейных стационарных систем раздел теории динамических систем, изучающая поведение и динамические свойства линейных стационарных систем (ЛСС). Широко используется в процессе управления техническими системами, цифровой обработке сигналов и … Википедия

Стационарная гидростатическая система — Прибор для измерения осадок фундаментов, состоящий из большого числа водомерных стаканов пьезометров, жестко укрепленных на фундаментах или конструкциях здания (сооружения) Источник: ГОСТ 24846 81: Грунты. Методы измерения деформаций оснований… … Словарь-справочник терминов нормативно-технической документации

Система небесных координат — используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере.… … Википедия

система пенного тушения пожаров стационарная (неавтоматическая) — Совокупность стационарных технических средств для тушения пожара за счет выпуска пены. Примечание Средства автоматизации этих систем должны обеспечить включение основных и резервных насосов в случае, если основные неисправны или не обеспечивают… … Справочник технического переводчика

Система стационарная пенного пожаротушения (неавтоматическая) — комплект оборудования, включающий резервуары для воды и пенообразователя, насосную станцию и сеть растворопроводов с пожарными гидрантами. Средства автоматизации систем должны обеспечить включение резервных насосов в случае, если основные… … Словарь-справочник терминов нормативно-технической документации

Источник

Линейная стационарная система

Теория линейных стационарных систем — раздел теории динамических систем, изучающая поведение и динамические свойства линейных стационарных систем (ЛСС). Широко используется в процессе управления техническими системами, цифровой обработке сигналов и других областях инженерного дела.

Содержание

Обзор

Определяющими свойствами для любой линейной стационарной системы являются линейность и стационарность:

Динамика систем, обладающих вышеперечисленными свойствами, может описываться одной простой функцией, к примеру, импульсной переходной функцией. Выход системы может рассчитываться как свёртка входного сигнала с импульсной переходной функцией системы. Этот метод анализа иногда называется анализом во временной области. Сказанное справедливо и для дискретных систем.

Кроме того, любая ЛСС может быть описана в частотной области с помощью своей передаточной функции, которая является преобразование Лапласа импульсной передаточной функции (или Z-преобразованием в случае дискретных систем). В силу свойств этих преобразований, выход системы в частотной области будет равен произведения передаточной функции и соответсвующего преобразования входного сигнала. Другими словами, свёртке во временной области соответсвует умножение в частотной области.

Так как синусоиды представляют собой сумму компелксных экспонент с комплексно-сопряжёнными частотами, если вход системы — синусоида, то выходом системы будет также синусоида, в общем случае с другой амплитудой и фазой, но с той же частотой.

Теория ЛСС хорошо подходит для описания многих систем. Большинство ЛСС гораздо проще анализировать, чем нестационарные и нелинейные системы. Любая система, динамика которой описывается линейным дифференциальным уравнением с постоянными коэффициентами, является линейной стационарной системой. Примерами таких систем являются электрические схемы, собранные из резисторов, конденсаторов и катушек индуктивности (RLC-цепочки). Груз на пружинке также можно считать ЛСС.

Большая часть общих концепций ЛСС схожа как в случае непрерывных систем, так и в случае дискретных систем.

Стационарность и линейные преобразования

Для дискретной системы:

Так как — линейный оператор, воздействие системы на входной сигнал x(t) представляется линейным преобразованием, описываемым следующим интегралом (интеграл суперпозиции)

Если линейный оператор 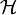ко всему прочему является и стационарным, тогда

Для краткости записи второй аргумент в h(t₁,t₂) обычно опускается и интеграл суперпозиции становится интегралом свёртки:

Таким образом, интеграл свёртки показывает как линейная стационарная система отрабатывает любой входной сигнал. Полученное соотношение для дискретных систем:

Импульсная переходная функция

Если ко входу системы приложить входной сигнал в виде дельта-функции Дирака, результирующий выходной сигнал ЛСС будет представлять собой импульсную переходную функцию системы. Запись:

Для дискретной системы:

(из-за свойства сдвига дельта-функции).

то есть h(t) — импульсная переходная функция системы

Импульсная переходная функция используется для того, чтобы найти выходной сигнал системы как реакцию на любой входной сигнал. Кроме того, любой вход может быть представлен в виде суперпозиции дельта-функций:

Приложив ко входу системы, получим:

(так как линейна) (так как x(τ) постоянна по t и линейна) (by definition of h(t) )

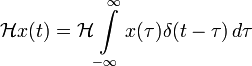
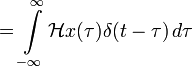
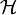
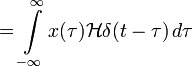
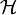
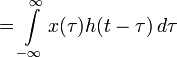
В импульсной переходной функции h(t) содержится вся информация о динамике ЛСС.

Собственные функции

Собственная функция — функция, для которой выход оператора представляет собой ту же функцию, в общем случае с точностью до постоянного множителя. Запись:

,

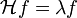
где f — собственная функция, и λ — собственное число, константа.

что эквивалентно следующему выражению в силу коммутативности свёртки:

,

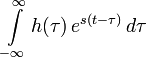
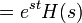
зависит только от s.

Таким образом, e st — собственная функция ЛСС.

Преобразования Лапласа и Фурье

Преобразование Лапласа обычно используется для односторонних сигналов, то есть при нулевых начальных условиях. Начальный момент времени без потери общности принимается за ноль, а преобразование берётся от ноля до бесконечности (преобразование, которое получается при интегрировании также и до минус бесконечности, называется двустороннее преобразование Лапласа).

Преобразование Фурье используется для анализа систем, через которые проходят периодические сигналы, и во многих других случаях — например, для анализа системы на устойчивость.

Из-за свойств свёртки для обоих преобразований имеют место следующие соотношения:

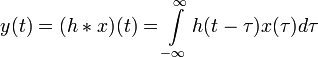
Для дискретных систем:

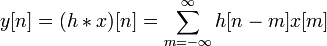
Некоторые свойства

Некоторые из важных свойств любой системы — причинность и устойчивость. Для того, чтобы система существовала в реальном мире, должен выполняться принцип причинности. Неустойчивые системы могут быть построены и иногда быть даже полезными.

Причинность

Система называется причинной, если её выход зависит только от текущего или предыдущего приложенного воздействия. Необходимое и достаточное условие причинности:

Для дискретных систем:

где h(t) — импульсная переходная функция. В явном виде определить причинная система или нет из её преобразования Лапласа в общем случае невозможно, так как обратное преобразование Лапласа не является уникальным. Причинность может быть определена когда задана область сходимости.

Устойчивость

Система является устойчивой по ограниченному входу, ограниченному выходу (англ. bounded input, bounded output stable, BIBO stable ) если для каждого ограниченного входа выходной сигнал является конечным. Запись: Если

Для дискретных систем:

См. также

Ссылки

Статьи, связанные с теорией управления и моделированиемОсновные понятияДинамическая система • Математическая модель • Передаточная функция • Пространство состоянийКлассификация системЛинейные стационарные системы (ЛСС)Фундаментальные свойства системУстойчивость • Наблюдаемость • УправляемостьДругоеИдентификация системСмежные понятияПреобразование Лапласа • Z-преобразование • Преобразование Фурье • Дельта-функцияХарактеристики системИмпульсная переходная характеристика • АФЧХ • ЛАФЧХСпособы математического описания
динамических системПередаточная функция • Пространство состоянийРазноеАвтоматика и телемеханика

Полезное

Смотреть что такое «Линейная стационарная система» в других словарях:

Теория линейных стационарных систем — раздел теории динамических систем, изучающий поведение и динамические свойства линейных стационарных систем (ЛСС). Широко используется в процессе управления техническими системами, цифровой обработке сигналов и других областях инженерного дела.… … Википедия

ЛСС — Теория линейных стационарных систем раздел теории динамических систем, изучающая поведение и динамические свойства линейных стационарных систем (ЛСС). Широко используется в процессе управления техническими системами, цифровой обработке сигналов и … Википедия

ЛСС — Латвийский союз самоуправлений Латвия Источник: http://www.regnum.ru/news/304683.html ЛСС линейные сооружения связи воен., связь Источник: http://www.rksi.ru/dopo/programs.shtml ЛСС летучее сернистое соединение … Словарь сокращений и аббревиатур

ГОСТ Р 53953-2010: Электросвязь железнодорожная. Термины и определения — Терминология ГОСТ Р 53953 2010: Электросвязь железнодорожная. Термины и определения оригинал документа: 39 (железнодорожная) телеграфная сеть: Сеть железнодорожной электросвязи, представляющая собой совокупность коммутационных станций и узлов,… … Словарь-справочник терминов нормативно-технической документации

Векторная авторегрессия — (VAR, Vector AutoRegression) модель динамики нескольких временных рядов, в которой текущие значения этих рядов зависят от прошлых значений этих же временных рядов. Модель предложена Кристофером Симсом как альтернатива системам одновременных… … Википедия

ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… … Физическая энциклопедия

Список медицинских сокращений — Эта страница глоссарий. # А … Википедия

Геостационарная орбита — (ГСО) круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси. В горизонтальной системе… … Википедия

Волгодонск — Город Волгодонск Флаг Герб … Википедия

Белорусы — Белорусы … Википедия

Источник

СТАЦИОНАРНЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ

Такова взаимосвязь: раз существует гадание, значит должны быть и боги; а раз существуют боги, значит должно быть и гадание.

Марк Туллий Цицерон. О гадании.

Римский философ и политик, I в.д.н.э.

Содержание: Введение. 11.1. Линейные системы. Общие понятия систем. Линейные системы. Основные системные операции. Инвариантность систем к сдвигу. Математическая модель системы. Нерекурсивные цифровые системы. Рекурсивные цифровые системы. Стационарные и нестационарные системы. 11.2. Импульсная характеристика системы. Импульсный отклик системы. Реакция системы на произвольный сигнал. Усиление постоянной составляющей сигнала. Усиление шумов. Определение импульсной реакции. 11.3. Передаточные функции цифровых систем. Z-преобразование. Устойчивость систем. 11.4. Частотные характеристики систем. Основные свойства. 11.5. Реакция систем на случайные сигналы. Математическое ожидание. Корреляционные соотношения. Спектральные соотношения. Дисперсия выходного сигнала. Функция когерентности. 11.6. Структурные схемы систем. Структурные схемы. Графы систем. Соединения систем. Схемы реализации систем. Обращенные формы. Литература.

Для определения системы необходимо задать характер, тип и области допустимых величин входных и выходных сигналов. Как правило, системы выполняются на сигналы одного типа по входу/выходу и подразделяются на системы непрерывного времени (аналоговые или дискретные сигналы на входе и выходе) и цифровые системы. Совокупность системного оператора Т и пространства сигналов образует математическую модель системы.

Линейные системы составляют основной класс систем обработки сигналов. Термин линейности означает, что система преобразования сигналов должна иметь произвольную, но в обязательном порядке линейную связь между входным сигналом (возбуждением) и выходным сигналом (откликом). В нелинейных системах связь между входным и выходным сигналом определяется произвольным нелинейным законом.

Система считается линейной, если в пределах установленной области входных и выходных сигналов ее реакция на входные сигналы аддитивна (выполняется принцип суперпозиции сигналов) и однородна (выполняется принцип пропорционального подобия).

Принцип аддитивности требует, чтобы реакция на сумму двух входных сигналов была равна сумме реакций на каждый сигнал в отдельности:

Принцип однородности или пропорционального подобия требует сохранения однозначности масштаба преобразования при любой амплитуде входного сигнала:

Другими словами, отклик линейной системы на взвешенную сумму входных сигналов должен быть равен взвешенной сумме откликов на отдельные входные сигналы независимо от их количества и для любых весовых коэффициентов, в том числе комплексных.

y(t 1 +t 2 ) = a 2 (t 1 +t 2 ) = a 2 t 1 +a 2 t 2 = y(t 1 )+y(t 2 ). Система аддитивна.

cy(t) = ca 2 t = a 2 ct = y(сt). Система однородна. И в целом линейна.

При программной реализации линейных систем на ЭВМ особых затруднений с обеспечением линейности в разумных пределах значений входных и выходных сигналов, как правило, не возникает. При физической (аппаратной) реализации систем обработки данных диапазон входных и/или выходных сигналов, в котором обеспечивается линейность преобразования сигналов, всегда ограничен и должен быть специально оговорен в технической документации или методической инструкции.

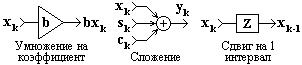
Основные системные операции. К базовым линейным операциям, из которых могут быть сформированы любые линейные операторы преобразования, относятся операции скалярного умножения, сдвига и сложения сигналов:

Графическое отображение операций (цифровая форма) приведено на рис. 11.1.1.

где u(x,y) – двумерный входной сигнал, c(x,y) – пространственная маска постоянных (весовых) коэффициентов. Пространственное маскирование представляет собой поэлементное произведение значений сигнала с коэффициентами маски.

Инвариантность систем к сдвигу. Система называется инвариантной к сдвигу (инвариантной во времени, а равно и по любым другим аргументам), если сдвиг входного сигнала по аргументам вызывает соответствующий сдвиг выходного сигнала:

s(x,t) = T[a(x,t)], T[a(x- D x,t- D t)] = s(x- D x,t- D t).

Линейность и инвариантность к сдвигу являются независимыми свойствами систем и не определяют друг друга. Так, например, операция квадратирования сигнала (возведения в квадрат всех значений сигнала) инвариантна к сдвигу, но нелинейна.

Математическая модель системы задается связью между сигналами входа и выхода и в аналоговой одномерной линейной системе обычно выражается линейным дифференциальным уравнением :

a m = b n . (11.1.1)

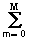
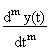
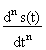
При нормировке к а о = 1, отсюда следует :

y(t) =b n —a m . (11.1.1′)

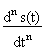
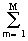
По существу, правой частью этого выражения в самой общей математической форме отображается содержание операции преобразования входного сигнала, т.е. задается оператор трансформации входного сигнала в выходной.

Аналогичная связь в цифровой системы описывается разностными уравнениями :

a m y((k-m) D t) = b n s((k-n) D t). (11.1.2)

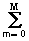
Нерекурсивные цифровые системы. При нулевых значениях коэффициентов a m уравнение (11.1.2′) переходит в уравнение дискретной свертки x(k) с оператором b n :

y(k) =b n x(k-n). (11.1.3)

При обработке данных на ЭВМ ограничение по каузальности системного оператора снимается. В программном распоряжении системы могут находиться как «прошлые», так и «будущие» значения входных отсчетов, при этом уравнение (11.1.3) будет иметь вид:

y(k) =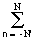b n x(k-n). (11.1.3′)

При N’ = N система называется двусторонней симметричной. Симметричные системы, в отличие от каузальных, не изменяют фазы обрабатываемых сигналов.

Техника выполнения свертки в координатной области не отличается от техники выполнения обычной дискретной свертки двух массивов данных.

Описанный процесс свертки в вещественной области массива данных x(k) с нерекурсивным оператором системы b n (массивом весовых коэффициентов системы) обычно называют нерекурсивной цифровой фильтрацией данных, а саму систему, если она выполняет только данную операцию, нерекурсивным цифровым фильтром (НЦФ).

Пример. Сглаживание данных скользящим симметричным П-окном размером 5 отсчетов.

Проверьте результат (выполните фильтрацию сигнала).

Заметим: сумма коэффициентов b n сглаживающего НЦФ равна 1, при этом сумма значений выходного сигнала равна сумме значений входного сигнала. Сигнал «размазался» по аргументу.

Рекурсивные цифровые системы. Системы, которые описываются полным разностным уравнением (11.1.2), принято называть рекурсивными цифровыми системами (РЦС) или рекурсивными цифровыми фильтрами (РЦФ), так как в вычислении текущих значений выходного сигнала участвует не только входной сигнал, но и значения выходного сигнала, вычисленные в предшествующих циклах расчетов. С учетом последнего фактора рекурсивные системы называют системами с обратной связью. Пример рекурсивной системы приведен на рис. 11.1.3.

Расчет выходного сигнала:

y 4 = 0,5x 4 + 0,5y 3 = 0.625 y 5 = 0,5x 5 + 0,5y 4 = 0.3125 и т.д.

Выходной сигнал: y k =

Из примера можно видеть, что реакция РЦС на конечный входной сигнал, в принципе, может иметь бесконечную длительность, в отличие от реакции НЦС, которая всегда ограничена количеством членов b k (окном системы).

Расчет выходного сигнала:

y 4 = x 4 +y 3 +y 2 = 3. y 5 = x 5 +y 4 +y 3 = 5. y 6 = x 6 +y 5 +y 4 = 8. y 7 = x 7 +y 6 +y 5 = 13. и т.д.

Заметим: сумма коэффициентов обратной связи a i больше 1 и выходной сигнал идет «в разнос».

Пример. Интегрирование данных по формуле трапеций.

Стационарные и нестационарные системы. Система считается стационарной и имеет постоянные параметры, если ее свойства (математический алгоритм оператора преобразования) в пределах заданной точности не зависят от входного и выходного сигналов и не изменяются ни во времени, ни от каких-либо других внешних факторов. Математически это означает задание системы уравнениями типа (11.1.1-2) с постоянными значениями коэффициентов a j и b i и реакция системы на какое-либо воздействие не зависит от времени (координат) его приложения. В противном случае система является нестационарной или параметрической (системой с переменными параметрами). Среди последних большое значение имеют так называемые адаптивные системы обработки данных. В этих системах производится, например, оценивание определенных параметров входных и выходных сигналов, по результатам сравнения которых осуществляется подстройка параметров преобразования (переходной характеристики системы) таким образом, чтобы обеспечить оптимальные по производительности условия обработки сигналов или минимизировать погрешность обработки.

11.2. Импульсная характеристика системы [1,5]

y(t) = T[ d (t)] є h(t). (11.2.1)

y(k D t) = T[ d (k D t)] є h(k D t). (11.2.1′)

Для цифровых систем импульсный отклик однозначно определяется реакцией системы на импульс Кронекера d (k D t)=1 при k=0.

Функцию импульсного отклика называют также весовой функцией системы.

Реакция системы на произвольный сигнал. Если функция импульсного отклика системы известна, то, с учетом принципа суперпозиции сигналов в линейной системе, можно выполнить расчет реакции системы в любой произвольный момент времени на любое количество входных сигналов с любыми моментами времени их прихода путем суммирования запаздывающих реакций системы на эти входные сигналы, как это показано на рис. 11.2.1 для трех входных импульсов. В общем случае произвольный сигнал на входе системы может быть разложен в линейную последовательность взвешенных единичных импульсов:

y(t) = T[s(t)] є T[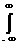s( t ) d (t- t ) d t]. (11.2.2)

На основании принципа суперпозиции линейный оператор Т может быть внесен под знак интеграла, т.к. последний представляет собой предельное значение суммы. При этом операция преобразования действует только по переменной t:

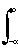
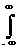
y(t) =s( t ) Т[ d (t- t )] d t = s( t ) h(t- t ) d t. (11.2.3)

Это выражение представляет собой интеграл Дюамеля или свертку (конволюцию) входного сигнала с импульсной характеристикой системы. Заменой переменных t- t = t можно убедиться в том, что эта операция, как и положено свертке, коммутативна:

Аналогично, для дискретных сигналов:

y(k D t) =s(n D t) h(k D t-n D t) є h(n D t) s(k D t-n D t). (11.2.3′)

В символической форме математического представления:

y(t) = s( t ) * h(t- t ) є s(t- t ) * h( t ) є s(t) * h(t).

В реальных физических системах импульсный отклик h(t) равен нулю при t

Усиление постоянной составляющей сигнала. Подадим на вход системы постоянный сигнал s(t) = A. При этом сигнал на выходе системы:

т.е. площадь импульсного отклика (для цифровой системы соответственно сумма коэффициентов импульсного отклика) является коэффициентом К пс усиления постоянной составляющей входного сигнала. Если при обработке сигналов должны изменяться только динамические характеристики их формы без изменения постоянной составляющей, а равно и различных постоянных уровней (фона, пьедесталов, региональных трендов и т.п.), то площадь импульсного отклика (сумма коэффициентов) должна нормироваться к единице.

y(k) = 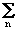h(n)[x(k-n)+ e (k-n)].

Математическое ожидание значений выходного сигнала:

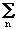
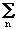
M < y(k) >= h(n)[x(k-n)+M < e (k-n) >] = h(n) x(k-n).

Вычислим дисперсию распределения отсчетов выходного сигнала:

Если правую часть последнего выражения представить в виде

то в этом выражении математические ожидания всех членов произведения с сомножителями e (n) e (m) при n № m равны 0 в силу статистической независимости значений шума. Остаются только члены с n = m, т.е.:

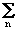
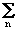
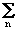
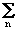
M <h 2 (n) e 2 (n) > = h 2 (n) M < e 2 (n) >= D e h 2 (n) = s 2 h 2 (n). (11.2.5)

Отсюда следует, что сумма квадратов значений нормированного импульсного отклика системы представляет собой коэффициент усиления аддитивных шумов во входном сигнале.

Пример. Сглаживающий фильтр: y(k) = 0.2 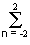x(k-n).

Коэффициент усиления шумов: 5 (0.2 2 ) = 0.2. Дисперсия шумов уменьшается в 1/0.2 = 5 раз.

,

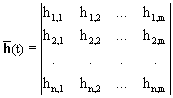
а выражение свертки приобретает вид:

=d t.

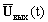
Определение импульсной реакции требуется, как правило, для рекурсивных систем, так как импульсная реакция для НЦС специального определения не требует:

h(k) =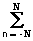b(n) d (k-n) є b(k).

Если выражение для системы известно в общей форме (11.1.2), определение импульсной реакции производится подстановкой в уравнение системы импульса Кронекера с координатой k = 0 при нулевых начальных условиях, при этом сигнал на выходе системы будет представлять собой импульсную реакцию системы: y(k) є h(k).

Расчет выходного сигнала при нулевых начальных условиях:

Определение импульсной реакции физических систем обычно производится подачей на вход систем ступенчатой функции u o (k) = 1 при k і 0, и u o (k) = 0 при k

g(k) =h(n) u o (k-n) =h(n).

Функция g(k) получила название переходной характеристики системы (перехода из одного статического состояния в другое).

Z-преобразование является удобным методом решения разностных уравнений линейных систем. Применяя z-преобразование к обеим частям равенства (11.1.2), получаем:

H(z) = Y(z)/X(z) =b n z n (1+a m z m ). (11.3.2)

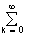
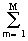
Для нерекурсивных систем при a m = 0:

т.е. передаточная функция системы является z-образом ее импульсной реакции. При обратном z-преобразовании передаточной функции соответственно получаем импульсную характеристику системы:

Если функция H(z) представлена конечным степенным полиномом, как это обычно имеет место для НЦС, то обратное z-преобразование элементарно. Передаточная функция РЦС также может быть представлена степенным полиномом прямым делением числителя на знаменатель правой части выражения (11.3.2), однако результат при этом может оказаться как конечным, так и бесконечным, т.е. система может иметь либо конечную, либо бесконечную импульсную характеристику. Системы с бесконечной импульсной характеристикой получили название БИХ-систем, с конечной импульсной характеристикой соответственно КИХ-систем. Нерекурсивные системы всегда имеют конечную импульсную характеристику, т.к. длительность импульсной реакции НЦС определяется окном фильтра.

Пример. Передаточная функция рекурсивной системы: H(z) = (1-z 5 )/(1-z).

Система имеет конечную импульсную характеристику.

Система имеет бесконечную импульсную характеристику.

Для конечного по энергии входного сигнала, можно записать:

Отсюда следует условие, при котором выходной сигнал системы также будет ограниченным:

т.е. необходимым и достаточным условием устойчивости системы является абсолютная сходимость ее импульсной характеристики, или, для цифровых систем, абсолютная суммируемость импульсного отклика:

Анализ устойчивости может быть проведен по передаточной функции. В устойчивой системе значение H(z) должно быть конечным во всех точках z-плоскости, где |z| Ј 1, а, следовательно, передаточная функция не должна иметь особых точек (полюсов) при z Ј 1 (на и внутри единичного круга на z-плоскости). Полюсы определяются корнями многочлена знаменателя передаточной функции H(z).

Приведенный критерий устойчивости относится к несократимой дроби, т.к. в противном случае возможна компенсация полюса нулем передаточной функции и следует проверить наличие однозначных нулей и полюсов.

Проверка на устойчивость требуется только для рекурсивных цифровых фильтров (систем с обратной связью), нерекурсивные системы всегда устойчивы.

11.4. Частотные характеристики систем [2,5].

Для линейных систем, принимая в качестве сигнала на входе системы собственную функцию x(k D t) = B( w )exp(j w k D t), мы вправе ожидать на выходе системы сигнал y(k D t) = A( w )exp(j w k D t). Подставляя эти выражения в разностное уравнение системы (11.1.2), получаем:

a m A( w )exp(j w k D t-j w m D t) =b n B( w )exp(j w k D t-j w n D t).

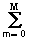
A( w )exp(j w k D t)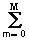a m exp(-j w m D t) = B( w )exp(j w k D t)b n exp(-j w n D t).

A( w )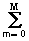a m exp(-j w m D t) = B( w )b n exp(-j w n D t). (11.4.1)

Отсюда, частотная передаточная функция системы (частотная характеристика при нормировке к а о =1):

H( w ) = A( w )/B( w ) =b n exp(-j w n D t)[1+a m exp(-j w m D t)]. (11.4.2)

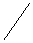
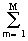
Нетрудно убедиться, что подстановкой z = exp(-j wD t) в выражение передаточной функции H(z) (11.3.2) может быть получено абсолютно такое же выражение для частотной характеристики, т.е.:

H( w ) є H(z) при z = exp(-j wD t).

При обратном преобразовании H(z) во временную область с использованием выражений (11.3.4-5) отсюда следует также, что частотная характеристика системы представляет собой Фурье-образ ее импульсной реакции, и наоборот. При D t = 1:

H( w ) =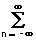h(n) exp(-j w n), (11.4.3)

A( w ) = |H( w )| = .

j ( w ) = arctg(Im H( w )/Re H( w )).

Основные свойства частотных характеристик систем:

1. Частотные характеристики являются непрерывными функциями частоты.

11.5. Реакция систем на случайные сигналы [2,14].

Если сигнал на входе линейной системы является детерминированным, то, при известных параметрах системы, его соотношение с выходным сигналом является однозначным. Таким же однозначным является соотношение процессов на входе и выходе и для случайных сигналов, однако в силу природы последних явное представление, как входного сигнала, так и отклика системы, не представляется возможным. Для описания отклика системы необходимо использовать статистический подход. При рассмотрении данной темы ограничимся только физически реализуемыми системами с односторонним импульсным откликом h(t) (h(t)=0 при t

Квазидетерминированный сигнал в какой-то мере позволяет оценить сохранение однозначности преобразования системой случайных сигналов.

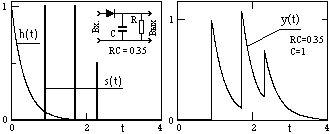
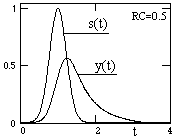
Допустим, что система имеет импульсный отклик h(t) = exp(-at), t і 0. Квазидетерминированный случайный сигнал стационарен, не обладает свойством эргодичности, но может быть описан в явной математической форме. Зададим сигнал на входе системы следующего вида:

y(t) = h( t ) * x(t- t ) є h( t ) Ч x(t- t ) d t = A/3 + [3 cos(2t+ j ) + 2 sin(2t+ j )]/13.

Из выражения следует, что выходной сигнал системы также является случайным процессом и содержит те же самые случайные параметры, что и входной сигнал, а, следовательно, для него также могут быть определены статистические характеристики.

Математическое ожидание произвольного случайного стационарного сигнала x(t) на выходе линейной системы определится выражением:

Отсюда следует, что математическое ожидание выходных сигналов системы равно математическому ожиданию входных сигналов, умноженному на коэффициент усиления системой постоянной составляющей. Если система не пропускает постоянную составляющую сигналов (площадь или сумма коэффициентов импульсного отклика системы равна нулю), то случайный выходной сигнал всегда будет иметь нулевое математическое ожидание.

Корреляционные соотношения. Для произведения выходных сигналов y(t) и y(t+ t ) линейной системы можно записать:

Если взять математические ожидания от обеих частей этого равенства, то, с учетом соотношения в подынтегральном выражении

Таким образом, функция автокорреляции (АКФ) выходного сигнала равна АКФ входного сигнала, свернутой дважды, в прямом и обратном направлении, с импульсным откликом системы, что сохраняет четность АКФ выходного сигнала. Для нецентрированных процессов аналогичное заключение действительно и для ковариационных функций.

Заметим, что для свертки импульсных откликов, производя замену t-b = t, мы имеем равенство:

R y ( t ) = R x ( t ) * K h ( t ). (11.5.2′)

Это означает появление в случайном сигнале на выходе системы определенной корреляционной зависимости, вызванной инерционностью системы, причем радиус корреляции выходного сигнала обратно пропорционален верхней частоте, пропускаемой системой.

Для взаимной корреляционной функции (ВКФ) R xy входного и выходного сигналов соответственно имеем:

Другая взаимно корреляционная функция R yx может быть получена из соотношения:

R yx ( t ) = R xy (- t ) є R x ( t ) * h( t+a ). (11.5.4)

Отметим, что для статистически независимых случайных величин при одностороннем импульсном отклике h( t )=0 при t xy ( t ) также является односторонней и равна 0 при t yx соответственно равна 0 при t >0.

Применяя преобразование Фурье к выражениям (11.5.2), для спектра мощности выходного сигнала получаем:

Спектр мощности сигнала на выходе системы равен спектру мощности входного сигнала, умноженному на квадрат модуля частотной характеристики фильтра. С учетом четности корреляционных функций спектр мощности выходного сигнала также является четной действительной функцией и не имеет фазовой характеристики процесса.

Аналогично, для взаимного спектра мощности на основе выражений (11.5.3-4):

W xy (f) = W x (f) H(f). (11.5.6)

Взаимный спектр мощности при одностороннем импульсном отклике является комплексным и содержит как амплитудную, так и фазовую характеристику процесса.

Отметим, что с использованием выражения (11.5.6) можно производить определение частотной характеристики и импульсного отклика системы:

Дисперсия выходного сигнала может быть определена с использованием формул (11.5.2,5):

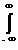
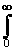
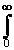
s y 2 = R y (0) =W x (f) |H(f)| 2 df є R x (0)h 2 (t) dt = s x 2 h 2 (t) dt, (11.5.7)

что полностью соответствует полученной ранее формуле (11.2.5) для цифровой системы.

Если сигнал нецентрированный и значение дисперсии входного сигнала неизвестно, то по аналогичным формулам вычисляется сначала средний квадрат выходного сигнала или так называемая средняя мощность сигнала :

== R y (0) є h 2 (t) dt є W x (f) |H(f)| 2 df, (11.5.8)

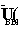
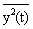
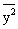
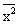
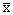
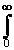
s y 2 = — 2 є (— 2 )h 2 (t) dt. (11.5.9)

Функция когерентности дает оценку точности принятой линейной модели системы. Когерентность входного и выходного сигналов системы оценивается по формуле:

g xy 2 (f) = |W xy (f)| 2 / [W x (f) Ч W y (f)]. (11.5.10)

Если функции W x (f) и W y (f) отличны от нуля и не содержат дельта-функций, то для всех частот f значения функции когерентности заключены в интервале:

1. Система осуществляет преобразование x(t) Ю y(t), но в измерениях этих сигналов или одного из них присутствует внешний шум. Так, например, в сигналах, зарегистрированных с ограничением по разрядности, появляется шум квантования (округления значений).

2. Система не является строго линейной. Это может наблюдаться, например, при определенном ограничении по разрядности вычислений в цифровых системах, при накоплении ошибки в рекурсивных системах и т.п.

3. Выходной сигнал y(t) помимо x(t) зависит еще от каких-то входных или внутренних системных процессов.

Величина 1- g xy 2 (f) задает долю среднего квадрата сигнала y(t) на частоте f, не связанную с сигналом x(t).

Использование функций когерентности в практических методах анализа случайных данных подробно рассмотрено в работе /2/.

11.6. Структурные схемы систем [5,20].

Структурные схемы. Алгоритмы обработки сигналов в системах наглядно отображаются в виде структурных схем. Базовые элементы схем и примеры построения структурных схем приводились ранее на рис. 11.1.1-3. Как правило, структурные схемы соответствуют программной реализации систем и будут рассматриваться ниже применительно к цифровым системам, но не определяет аппаратной реализации в специальных радиотехнических устройствах, которая может существенно отличаться от программной реализации, особенно для аналоговых систем.

Графы систем. Наряду со структурной схемой система может быть представлена в виде графа, который отображает диаграмму прохождения сигналов и состоит из направленных ветвей и узлов.

Соединения систем. Различают следующие соединения систем (рис. 11.6.2-4).

1. Последовательное соединение. Выходной сигнал предшествующей системы является входным для последующей. Эквивалентная передаточная функция общей системы равна произведению передаточных функций систем, в нее входящих:

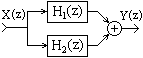
2. Параллельное соединение. Сигнал подается на входы всех параллельно соединенных систем одновременно, выходные сигналы систем суммируются. Эквивалентная передаточная функция общей системы равна сумме передаточных функций систем, в нее входящих:

H(z) = H 1 (z)+H 2 (z)+. +H N (z).

3. Соединение обратной связи. Выходной сигнал первой системы подается на выход системы и одновременно на вход системы обратной связи, выходной сигнал которой суммируется, со знаком плюс или минус в зависимости от вида связи (отрицательной или положительной), с входным сигналом первой системы. Эквивалентная передаточная функция общей системы: H(z) = H 1 (z)/(1 ± H 1 (z)H 2 (z)).

Схемы реализации систем. По принципам структурной реализации систем различают следующие схемы:

1. Прямая форма. Реализуется непосредственно по разностному уравнению

или по передаточной функции

H(z) =b n z n / (1+a m z m ).

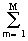
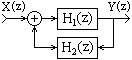
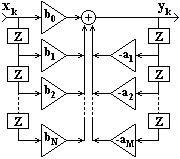
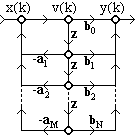
2. Прямая каноническая форма содержит минимальное число элементов задержки. Передаточную функцию РЦС можно представить в виде:

H(z) = Y(z)/X(z) = H 1 (z)H 2 (z),

y(k) =b n v(k-n). (11.6.2)

В разностных уравнениях (11.6.1-2) осуществляется только задержка сигналов v(k). Граф реализации РЦС приведен на рисунке 11.6.6.

3. Каскадная (последовательная) форма. Соответствует представлению передаточной функции в виде произведения:

H(z) =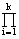H i (z).

H i (z) = (b 0 i +b 1 i Ч z+b 2 i Ч z 2 )/(1+a 1 i Ч z+a 2 i Ч z 2 ).

4. Параллельная форма. Используется много реже и соответствует представлению передаточной функции в виде суммы биквадратных блоков или более простых функций.

2. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с.

9. Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов. – М.: Мир, 1988. – 488 с.

14. Купер Дж., Макгиллем А. Вероятностные методы анализа сигналов и систем. – М.: Мир, 1989.

18. Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов. – М.: Связь, 1979. – 416 с.

20. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. – М.: Мир, 1978.

Источник