что такое стандартная функция
Что такое стандартная функция?
При решении различных задач с помощью компьютера бывает необходимо вычислить логарифм или модуль числа, синус угла и т.д.
| Вычисления часто употребляемых функций осуществляются посредством подпрограмм, называемых стандартными функциями, которые заранее запрограммированы и встроены в транслятор языка. |
Таблица стандартных функций школьного алгоритмического языка
| Название и математическое обозначение функции | Указатель функции | |
| Абсолютная величина (модуль) | | х | | abs(x) |
| Корень квадратный |  | sqrt(x) |
| Натуральный логарифм | ln x | ln(x) |
| Десятичный логарифм | lg x | lg(x) |
| Экспонента (степень числа е » 2.72) | e x | exp(x) |
| Знак числа x (-1,если х 0) | sign x | sign(x) |
| Целая часть х (т.е. максимальное целое число,не превосходящее х) | int(x) | |
| Минимум из чисел х и y | min(x,y) | |
| Максимум из чисел х и y | max(x,y) | |
| Частное от деления целого х на целое y | div(x,y) | |
| Остаток от деления целого х на целое y | mod(x,y) | |
| Случайное число в диапазоне от 0 до х-1 | rnd(x) | |
| Синус (угол в радианах) | sin x | sin(x) |
| Косинус (угол в радианах) | cos x | cos(x) |
| Тангенс (угол в радианах) | tg x | tg(x) |
| Котангенс (угол в радианах) | ctg x | ctg(x) |
| Арксинус (главное значение в радианах) | arcsin x | arcsin(x) |
| Арккосинус (главное значение в радианах) | arccos x | arccos(x) |
| Арктангенс (главное значение в радианах) | arctg x | arctg(x) |
| Арккотангенс (главное значение в радианах) | arcctg x | arcctg(x) |
В качестве аргументов функций можно использовать константы, переменные и выражения. Например:
| sin(3.05) min(a, 5) | sin(x) min(a, b) | sin(2*y+t/2) min(a+b, a*b) | sin((exp(x)+1)**2) min(min(a,b),min(c,d)) |
Каждый язык программирования имеет свой набор стандартных функций.
Как записываются арифметические выражения?
Арифметические выражения записываются по следующим правилам:
Примеры записи арифметических выражений
7.19. Что такое стандартная функция?
При решении различных задач с помощью компьютера бывает необходимо вычислить логарифм или модуль числа, синус угла и т.д.
| Вычисления часто употребляемых функций осуществляются посредством подпрограмм, называемых стандартными функциями , которые заранее запрограммированы и встроены в транслятор языка. |
Таблица стандартных функций школьного алгоритмического языка
| Название и математическое обозначение функции | Указатель функции | |
| Абсолютная величина (модуль) | | х | | abs(x) |
| Корень квадратный |  | sqrt(x) |
| Натуральный логарифм | ln x | ln(x) |
| Десятичный логарифм | lg x | lg(x) |
| Экспонента (степень числа е » 2.72) | e x | exp(x) |
| Знак числа x (-1,если х 0) | sign x | sign(x) |
| Целая часть х (т.е. максимальное целое число,не превосходящее х) | int(x) | |
| Минимум из чисел х и y | min(x,y) | |
| Максимум из чисел х и y | max(x,y) | |
| Частное от деления целого х на целое y | div(x,y) | |
| Остаток от деления целого х на целое y | mod(x,y) | |
| Случайное число в диапазоне от 0 до х-1 | rnd(x) | |
| Синус (угол в радианах) | sin x | sin(x) |
| Косинус (угол в радианах) | cos x | cos(x) |
| Тангенс (угол в радианах) | tg x | tg(x) |
| Котангенс (угол в радианах) | ctg x | ctg(x) |
| Арксинус (главное значение в радианах) | arcsin x | arcsin(x) |
| Арккосинус (главное значение в радианах) | arccos x | arccos(x) |
| Арктангенс (главное значение в радианах) | arctg x | arctg(x) |
| Арккотангенс (главное значение в радианах) | arcctg x | arcctg(x) |
В качестве аргументов функций можно использовать константы, переменные и выражения. Например:
| sin(3.05) min(a, 5) | sin(x) min(a, b) | sin(2*y+t/2) min(a+b, a*b) | sin((exp(x)+1)**2) min(min(a,b),min(c,d)) |
Каждый язык программирования имеет свой набор стандартных функций.
Что такое стандартная функция?
При решении различных задач с помощью компьютера бывает необходимо вычислить логарифм или модуль числа, синус угла и т.д.
| Вычисления часто употребляемых функций осуществляются посредством подпрограмм, называемых стандартными функциями, которые заранее запрограммированы и встроены в транслятор языка. |
Таблица стандартных функций школьного алгоритмического языка
| Название и математическое обозначение функции | Указатель функции | |
| Абсолютная величина (модуль) | | х | | abs(x) |
| Корень квадратный | sqrt(x) | |
| Натуральный логарифм | ln x | ln(x) |
| Десятичный логарифм | lg x | lg(x) |
| Экспонента (степень числа е » 2.72) | e x | exp(x) |
| Знак числа x (-1,если х 0) | sign x | sign(x) |
| Целая часть х (т.е. максимальное целое число,не превосходящее х) | int(x) | |
| Минимум из чисел х и y | min(x,y) | |
| Максимум из чисел х и y | max(x,y) | |
| Частное от деления целого х на целое y | div(x,y) | |
| Остаток от деления целого х на целое y | mod(x,y) | |
| Случайное число в диапазоне от 0 до х-1 | rnd(x) | |
| Синус (угол в радианах) | sin x | sin(x) |
| Косинус (угол в радианах) | cos x | cos(x) |
| Тангенс (угол в радианах) | tg x | tg(x) |
| Котангенс (угол в радианах) | ctg x | ctg(x) |
| Арксинус (главное значение в радианах) | arcsin x | arcsin(x) |
| Арккосинус (главное значение в радианах) | arccos x | arccos(x) |
| Арктангенс (главное значение в радианах) | arctg x | arctg(x) |
| Арккотангенс (главное значение в радианах) | arcctg x | arcctg(x) |
В качестве аргументов функций можно использовать константы, переменные и выражения. Например:
| sin(3.05) min(a, 5) | sin(x) min(a, b) | sin(2*y+t/2) min(a+b, a*b) | sin((exp(x)+1)**2) min(min(a,b),min(c,d)) |
Каждый язык программирования имеет свой набор стандартных функций.
Pascal. Стандартные функции и выражения
Стандартные функции.
В программировании, довольно часто приходиться выполнять однотипные действия, причем в задачах разного уровня и класса. И для ускорения процесса написания кода эти действия выносят в специальные подпрограммы – стандартные функции. Обращение к такой подпрограмме происходит по ее имени, а в скобках указывается значение аргумента. В следующей таблице указаны те стандартные функции, которые используются в языке программирования Pascal.
| Функция | Назначение |
| ABS(x) | Вычисление абсолютного значения x: |х| |
| SQR(x) | Вычисление квадрата x: x*x |
| SIN(x) | Вычисление синуса x: sin x |
| COS(x) | Вычисление косинуса x: cos x |
| ARCTAN(x) | Вычисление арктангенса x: arctg x |
| EXP(x) | Вычисление экспоненты (числа Е) в степени x |
| EXP10(x) | Вычисление 10 в степени x |
| LN(x) | Вычисление натурального логарифма x |
| LOG(x) | Вычисление десятичного логарифма x |
| SQRT(x) | Вычисление квадратного корня из x |
| A DIV B | Вычисление частного при делении А на В с отбрасыванием остатка |
| A MOD B | Нахождение остатка от делении А на В |
| TRUNC(x) | Нахождение целой части x |
| RANDOM(x) | Псевдослучайное число в интервале [0, x] |
| ROUND(x) | Округление значения x в сторону ближайшего целого |
| ODD(x) | Проверяет аргумент на нечетность. Результат TRUE, если аргумент нечетный, FALSE – если четный. |
| ORD(x) | Возвращает порядковый номер аргумента и, как следствие, преобразует величину порядкового типа в величину целого типа. |
| CHR(x) | Определение символа языка Паскаль по его порядковому номеру |
| SUCC(x) | Нахождение элемента, идущего после данного в перечне допустимых элементов |
| PRED(x) | Нахождение элемента, идущего перед данным в перечне допустимых элементов |
| FRAC(X) | Возвращает дробную часть x |
| INT(X) | Возвращает целую часть x |
| Pi | Значение математической постоянной π |
| EOF(x) | Возвращает TRUE, если файл находится в стоянии “конец файла”, иначе FALSE, если нет конца файла |
Выражения
Выражение состоит из переменных, констант, полей в записях, указателей функций, круглых скобок и знаков операций. Для корректной записи выражений необходимо знать не только как обозначаются те или иные операции, функции и т. п., но также стоит предусмотреть приоритеты их выполнения, математические и логические правила, а также некоторые тонкости самого языка. Для более углубленного изучения выражений, стоит рассмотреть несколько примеров.
1) 12+3*3=21 (12+3)*3=45
2) ( a >1) and ( a 3) (a+3>0) and (a+3 1) and (b
Логическая операция OR (или) суть дизъюнкция в логики и поэтому имеет следующую таблицу истинности:
Ложь имеет место только когда X и Y ложны (нули). В том случае, чтобы истина возвращалась только тогда, когда одно из условий верно следует применить оператор XOR (исключающее или):
(a+3>0) and (a+3 1) and (b
4) x ^( a ) = exp( a *ln( x ))
В Pascal нет функции возведения числа в степень (кроме степени 2), поэтому существует два пути:
1 — умножать число само на себя, какое то количество раз;
2 — воспользоваться функциями экспоненты и натурального логарифма.
В этом примере использованы оба варианта, но если степень, в которую необходимо возвести число, достаточно велика, то предпочтение следует отдать второму способу.
Что такое стандартная функция?
При решении различных задач с помощью компьютера бывает необходимо вычислить логарифм или модуль числа, синус угла и т.д.
| Вычисления часто употребляемых функций осуществляются посредством подпрограмм, называемых стандартными функциями, которые заранее запрограммированы и встроены в транслятор языка. |
Таблица стандартных функций школьного алгоритмического языка
| Название и математическое обозначение функции | Указатель функции | |
| Абсолютная величина (модуль) | | х | | abs(x) |
| Корень квадратный | sqrt(x) | |
| Натуральный логарифм | ln x | ln(x) |
| Десятичный логарифм | lg x | lg(x) |
| Экспонента (степень числа е » 2.72) | e x | exp(x) |
| Знак числа x (-1,если х 0) | sign x | sign(x) |
| Целая часть х (т.е. максимальное целое число, не превосходящее х) | int(x) | |
| Минимум из чисел х и y | min(x,y) | |
| Максимум из чисел х и y | max(x,y) | |
| Частное от деления целого х на целое y | div(x,y) | |
| Остаток от деления целого х на целое y | mod(x,y) | |
| Случайное число в диапазоне от 0 до х-1 | rnd(x) | |
| Синус (угол в радианах) | sin x | sin(x) |
| Косинус (угол в радианах) | cos x | cos(x) |
| Тангенс (угол в радианах) | tg x | tg(x) |
| Котангенс (угол в радианах) | ctg x | ctg(x) |
| Арксинус (главное значение в радианах) | arcsin x | arcsin(x) |
| Арккосинус (главное значение в радианах) | arccos x | arccos(x) |
| Арктангенс (главное значение в радианах) | arctg x | arctg(x) |
| Арккотангенс (главное значение в радианах) | arcctg x | arcctg(x) |
Как записываются арифметические выражения?
Арифметические выражения записываются по следующим правилам:
· Нельзя опускать знак умножения между сомножителями и ставить рядом два знака операций.
· Индексы элементов массивов записываются в квадратных (школьный АЯ, Pascal) или круглых (Basic) скобках.
· Для обозначения переменных используются буквы латинского алфавита.
· Операции выполняются в порядке старшинства: сначала вычисление функций, затем возведение в степень, потом умножение и деление и в последнюю очередь — сложение и вычитание.
· Операции одного старшинства выполняются слева направо. Например, a/b*c соответствует a/b*c. Однако, в школьном АЯ есть одно исключение из этого правила: операции возведения в степень выполняются справа налево. Так, выражение 2**(3**2) в школьном языке АЯ вычисляется как 2**(3**2) = 512. В языке QBasic аналогичное выражение 2^3^2 вычисляется как (2^3)^2 = 64. А в языке Pascal вообще не предусмотрена операция возведения в степень, в Pascal x^y записывается как exp(y*ln(x)), а x^y^z как exp(exp(z*ln(y))*ln(x)).
Примеры записи арифметических выражений
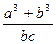
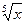, (x (больше), >= (больше или равно), = (равно), <> (не равно), а также логические операции и, или, не.