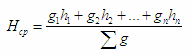что такое средняя высота
средняя высота
Смотреть что такое «средняя высота» в других словарях:
СРЕДНЯЯ ВЫСОТА СУШИ — в настоящее время соответствует высоте 875 м над совр. средним уровнем Мирового океана. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
средняя высота антенны — vidutinis antenos aukštis statusas T sritis radioelektronika atitikmenys: angl. antenna height above average terrain vok. mittlere Antennenhöhe, f rus. средняя высота антенны, f pranc. altitude moyenne de l antenne, f … Radioelektronikos terminų žodynas
Высота древостоя — (средняя) средняя высота совокупности деревьев, относящихся к основному ярусу. При глазомерно измерительном методе таксации среднюю высоту определяют как среднее арифметическое значение высот не менее трех деревьев, близких по таксационным… … Краткий словарь основных лесоводственно-экономических терминов
высота характерной волны — Средняя высота волны, измеренная от гребня к впадине, применительно к одной трети самых высоких волн. [ГОСТ Р 53389 2009] Тематики защита морской среды EN significant wave height … Справочник технического переводчика
Высота лесонасаждений — известной древесной породы служит, по Карлу Гейеру и Бауру, мерилом для измерения добротности местности в лесохозяйственном отношении, применительно к росту этой породы: с возрастанием ее, в данном возрасте, добротность местности увеличивается.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Средняя — периодическое увлажнение пола, при котором поверхность покрытия пола влажная или мокрая; покрытие пола пропитывается жидкостями. Источник: МДС 31 12.2007: Полы жилых, общественных и производственных зданий с применением м … Словарь-справочник терминов нормативно-технической документации
Средняя сопка — Координаты: Координаты … Википедия
Средняя часть — Ндп. Промежуточная часть пера Источник: ГОСТ 23537 79: Лопатки авиационных осевых компрессоров и турбин. Термины и определения оригинал … Словарь-справочник терминов нормативно-технической документации
Средняя Ель — Характеристика Длина 19 км Бассейн Белое море, Северный Ледовитый океан Бассейн рек Верхняя Лупья→Вычегда→Северная Двина Водоток … Википедия
Средняя Отока (приток Плюссы) — Средняя Отока (Либевица) Характеристика Длина 14 км Бассейн Балтийское море Бассейн рек → Плюсса → Нарва Водоток Исток … Википедия
средняя высота
Смотреть что такое «средняя высота» в других словарях:
СРЕДНЯЯ ВЫСОТА СУШИ — в настоящее время соответствует высоте 875 м над совр. средним уровнем Мирового океана. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
средняя высота антенны — vidutinis antenos aukštis statusas T sritis radioelektronika atitikmenys: angl. antenna height above average terrain vok. mittlere Antennenhöhe, f rus. средняя высота антенны, f pranc. altitude moyenne de l antenne, f … Radioelektronikos terminų žodynas
Высота древостоя — (средняя) средняя высота совокупности деревьев, относящихся к основному ярусу. При глазомерно измерительном методе таксации среднюю высоту определяют как среднее арифметическое значение высот не менее трех деревьев, близких по таксационным… … Краткий словарь основных лесоводственно-экономических терминов
высота характерной волны — Средняя высота волны, измеренная от гребня к впадине, применительно к одной трети самых высоких волн. [ГОСТ Р 53389 2009] Тематики защита морской среды EN significant wave height … Справочник технического переводчика
Высота лесонасаждений — известной древесной породы служит, по Карлу Гейеру и Бауру, мерилом для измерения добротности местности в лесохозяйственном отношении, применительно к росту этой породы: с возрастанием ее, в данном возрасте, добротность местности увеличивается.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Средняя — периодическое увлажнение пола, при котором поверхность покрытия пола влажная или мокрая; покрытие пола пропитывается жидкостями. Источник: МДС 31 12.2007: Полы жилых, общественных и производственных зданий с применением м … Словарь-справочник терминов нормативно-технической документации
Средняя сопка — Координаты: Координаты … Википедия
Средняя часть — Ндп. Промежуточная часть пера Источник: ГОСТ 23537 79: Лопатки авиационных осевых компрессоров и турбин. Термины и определения оригинал … Словарь-справочник терминов нормативно-технической документации
Средняя Ель — Характеристика Длина 19 км Бассейн Белое море, Северный Ледовитый океан Бассейн рек Верхняя Лупья→Вычегда→Северная Двина Водоток … Википедия
Средняя Отока (приток Плюссы) — Средняя Отока (Либевица) Характеристика Длина 14 км Бассейн Балтийское море Бассейн рек → Плюсса → Нарва Водоток Исток … Википедия
Турбо Таксатор
Отвод и таксация лесосек. Самый быстрый способ сделать работу
Что такое средняя высота насаждения и зачем ее определять?
Средняя высота является одной из основных лесотаксационных характеристик насаждения, отражающая особенности строения леса, его хозяйственную и промышленную ценность. В виду того, что в процессе таксации леса учесть индивидуальную высоту каждого дерева не представляется возможным, принято устанавливать среднюю высоту для всей совокупности деревьев, образующих насаждение.
Классическое определение высоты. Высота насаждения — это средняя высота совокупности деревьев в насаждении, относящихся к основной породе, основному возрастному поколению и основному ярусу. Зависит от древесной породы, условий местопроизрастания, возраста и осуществляемых в лесу хозмероприятий. Используется для определения класса бонитета; служит одним из запасообразующих компонентов.
В таксации леса чаще всего применяется 2 способа определения средней высоты, которые основываются на малой выборке наблюдений и тесной зависимости высоты деревьев от их диаметров. С увеличением среднего диаметра насаждения, как правило, увеличивается и его высота. При глазомерной таксации леса среднюю высоту определяют как среднеарифметическое значение высот не менее трех деревьев, близких к среднему дереву; на пробных площадях — по графику высот на основании среднего диаметра. Первый способ позволяет получить среднюю высоту с точностью до 5%, второй — при обычном измерении 10-25 учетных деревьев, представленных пропорционально площади поперечных сечений стволов ступенях толщины перечетной ведомости обеспечивает 2-3%-ную точность.
Для научных целей средняя высота определяется по способу Лоррея как высота, взвешенная через площадь сечения деревьев с учетом распределения их по ступеням толщины.
Стохастическая (вероятностная) связь высоты с рядом таксационных показателей позволяет использовать ее в качестве входа в важнейших нормативных документах: стандартных таблицах площадей сечений и запасов; товарных и сортиментных таблицах.
В производственной таксации лесов среднюю высоту определяются для установления разряда высот — входного показателя в сортиментные таблицы для материально-денежной оценки лесосек. Устанавливается разряд высот насаждения на основании соотношения высот и диаметров деревьев в трех центральных ступенях толщины. В сложных по форме древостоях разряды высот устанавливают не только для каждой древесной породы, но и для каждого яруса и поколения леса. Для определения разряда высот используют два метода измерения средней высоты насаждения:*
В первом случае производится измерение высоты у нескольких деревьев, относящихся к средним ступеням толщины, представленным наибольшим числом деревьев. Высота замеряется в 3-5 центральных ступенях толщины с измерением высот 3 модельных деревьев в каждой ступени. Затем для каждой ступени толщины выводят среднеарифметическую высоту. Полученный для соответствующих диаметров разряд высот сравнивают с данными разрядных таблиц и принимают решение какой разряд таблиц надо применить для расчета запаса древесины на лесосеке.
Во втором методе, основанном на принципе обмера среднего дерева в насаждении, определение разряда высот производят путем измерения высот и диаметров у 5 средних деревьев. Затем определяют среднеарифметичекие высоту и диаметр. По этим двум показателям в разрядных таблицах находят интервал высот, к которому относится найденная среднеарифметическая высота древостоя. Найденный интервал высот и определит искомый разряд высот древостоя.
* Программа материально-денежной оценки лесосек Турбо Таксатор позволяет рассчитать разряд высот по данным обмера модельных деревьев обеими методами
Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
| Разносторонний | Равнобедренный | Равносторонний |
| Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. | Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. | Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС. |
 |  |  |
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
Теперь найдем CD=AC-AD=54-24=30
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
pазбирался: Даниил Романович | обсудить разбор | оценить
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0
pазбирался: Даниил Романович | обсудить разбор | оценить