что такое средневзвешенная величина

Средневзвешенное значение — формула в Excel

В одной из предыдущих статей мы обсудили три основные функции для вычисления среднего в Excel, которые очень просты и просты в использовании.

Но что, если некоторые значения более важны, чем другие, и, следовательно, вносят больший вклад в конечное среднее значение? Например, если вы участвуете в экзаменах и все экзамены имеют одинаковый вес, они одинаково важны, то для вас важно именно среднее значение оценки.

Однако в реальной жизни это не всегда так. Например, если вы изучаете программирование, то насколько важны для вас оценки по истории и физкультуре по сравнению с оценками по профильным дисциплинам?

Некоторые задачи всегда важнее других. Некоторые экзамены важнее других.

В таких ситуациях вам как раз и необходимо рассчитывать средневзвешенное значение.

Хотя Microsoft Excel не предоставляет специальной функции взвешенного среднего, он предоставляет несколько других, которые окажутся полезными в ваших вычислениях, что показано в следующих примерах.

Что такое средневзвешенное значение?

Оно является своего рода средним арифметическим, в котором некоторые элементы набора данных имеют большую значимость, чем другие. Другими словами, каждому исходному показателю присваивается определенный вес.

В математике и статистике вы вычисляете взвешенное среднее значение, умножая каждое число в наборе на его вес, затем складываете произведения и делите итог сложения произведений на сумму всех весомостей.

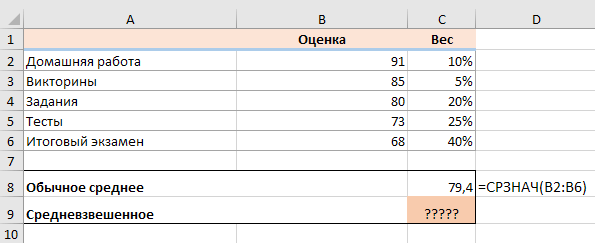
В этом примере, чтобы посчитать средневзвешенную итоговую оценку, вы умножаете каждый полученный балл на соответствующий процент (преобразованный в десятичную дробь), складываете эти 5 произведений вместе и делите это число на итог сложения пяти весов:

((91 * 0,1) + (85 * 0,05) + (80 * 0,2) + (73 * 0,25) + (68 * 0,4)) / (0,1 + 0,05 + 0,2 + 0,25 + 0,4) = 74,8

Формулы для средневзвешенного значения в Excel

В Microsoft Excel взвешенное среднее рассчитывается с использованием того же подхода, но с гораздо меньшими усилиями, поскольку функции Excel выполнят большую часть работы за вас.

Пример 1. Функция СУММ.

По сути, он выполняет те же вычисления, что и описанные выше, за исключением того, что вы предоставляете ссылки на ячейки вместо чисел.

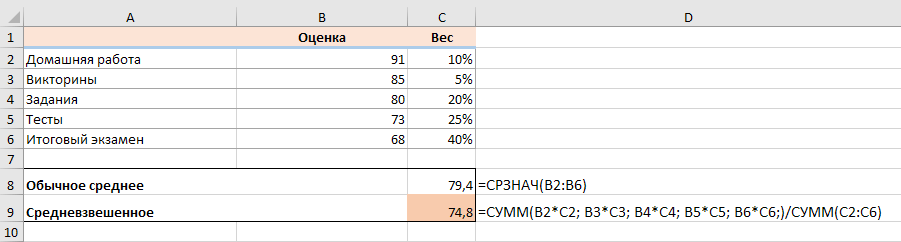
Посмотрите на рисунок чуть ниже: формула возвращает точно такой же результат, что и вычисления, которые мы делали минуту назад. Обратите внимание на разницу между нормальным средним, возвращаемым при помощи СРЗНАЧ в C8, и средневзвешенным (C9).

Несмотря на то, что формула эта очень проста и понятна, но она не подходит, если вы хотите усреднить большое количество элементов. Ведь придётся перечислять множество аргументов, что довольно утомительно.

В этом случае вам лучше использовать функцию СУММПРОИЗВ (SUMPRODUCT в английской версии). Об этом – ниже.

Пример 2. Функция СУММПРОИЗВ

Она идеально подходит для нашей задачи, так как предназначена для сложения произведений чисел. А это именно то, что нам нужно.

Таким образом, вместо умножения каждого числа на показатель его значимости по отдельности, вы предоставляете два массива в формуле СУММПРОИЗВ (в этом контексте массив представляет собой непрерывный диапазон ячеек), а затем делите результат на итог сложения весов:

= СУММПРОИЗВ(диапазон_значений ; диапазон_весов ) / СУММ( диапазон_весов )

Итак, формула умножает 1- е число в массиве 1 на 1- е в массиве 2 (в данном примере 91 * 0,1), а затем перемножает 2- е число в массиве 1 на 2- е в массиве 2 (85 * 0,15). в этом примере) и так далее. Когда все умножения выполнены, Эксель складывает произведения. Затем делим полученное на итог весов.

Чтобы убедиться, что функция СУММПРОИЗВ дает правильный результат, сравните ее с формулой СУММ из предыдущего примера, и вы увидите, что числа идентичны.

В нашем случае сложение весов дает 100%. То есть, это просто процент от итога. В таком случае верный результат может быть получен также следующими способами:

Но при использовании функции СУММ или СУММПРОИЗВ веса совершенно не обязательно должны составлять 100%. Однако, они также не должны быть обязательно выражены в процентах.

Например, вы можете составить шкалу приоритета / важности и назначить определенное количество баллов для каждого элемента, что и показано на следующем рисунке:

Видите, в этом случае мы обошлись без процентов.

Пример 3. Средневзвешенная цена.

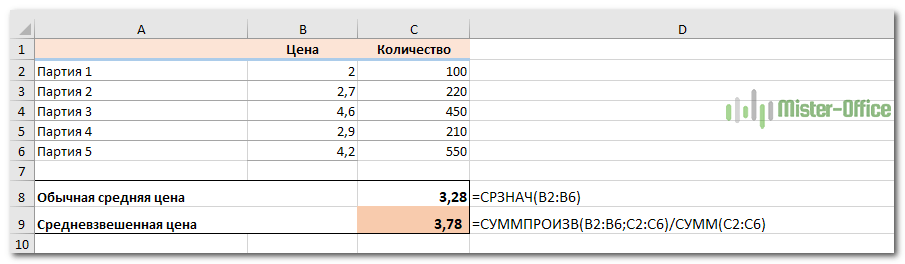
Еще одна достаточно часто встречающаяся проблема – как рассчитать средневзвешенную цену товара. Предположим, мы получили 5 партий товара от различных поставщиков. Мы будем продавать его по одной единой цене. Но чтобы ее определить, нужно знать среднюю цену закупки. В тот здесь нам и пригодится расчет средневзвешенной цены. Взгляните на этот простой пример. Думаю, вам все понятно.

Итак, средневзвешенная цена значительно отличается от обычной средней. На это повлияли 2 больших партии товара по высокой цене. А формулу применяем такую же, как и при расчете любого взвешенного среднего. Перемножаем цену на количество, складываем эти произведения, а затем делим на общее количество товара.

Ну, это все о формуле средневзвешенного значения в Excel.

Источник

Расчет средневзвешенного значения в Excel

Основная идея

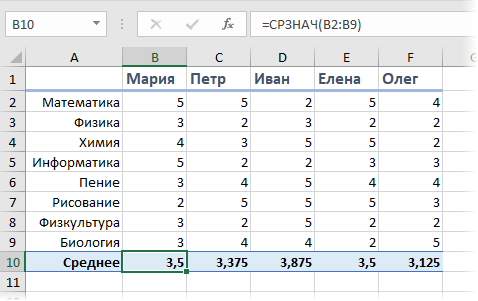
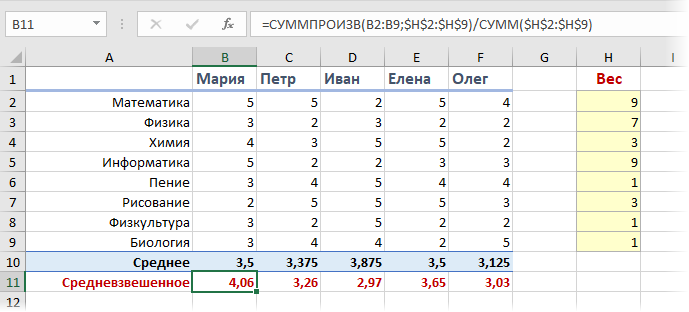
Предположим, что мы с вами сидим в приемно-экзаменационной комиссии и оцениваем абитуриентов, которые хотят поступить в наш ВУЗ. Оценки по различным предметам у наших кандидатов следующие:

На первый взгляд кажется, что лучше всех подходит Иван, т.к. у него средний бал максимальный. Но тут мы вовремя вспоминаем, что факультет-то наш называется «Программирование», а у Ивана хорошие оценки только по рисованию, пению и прочей физкультуре, а по математике и информатике как раз не очень. Возникает вопрос: а как присвоить нашим предметам различную важность (ценность), чтобы учитывать ее при расчете среднего? И вот тут на помощь приходит средневзвешенное значение.

В бизнесе средневзвешенное часто используется в таких задачах, как:

Расчет средневзвешенного формулами

Добавим к нашей таблице еще один столбец, где укажем некие безразмерные баллы важности каждого предмета по шкале, например, от 0 до 9 при поступлении на наш факультет программирования. Затем расчитаем средневзвешенный бал для каждого абитурента, т.е. среднее с учетом веса каждого предмета. Нужная нам формула будет выглядеть так:

Так что берем Машу, а Иван пусть поступает в институт физкультуры 😉

Расчет средневзвешенного в сводной таблице

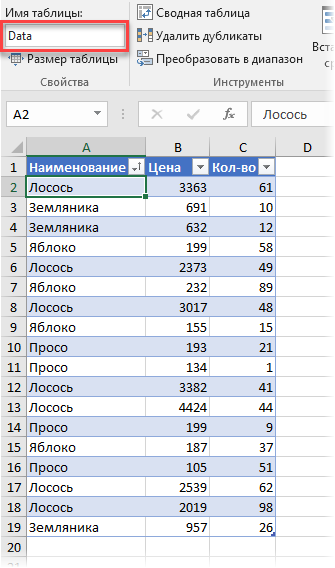
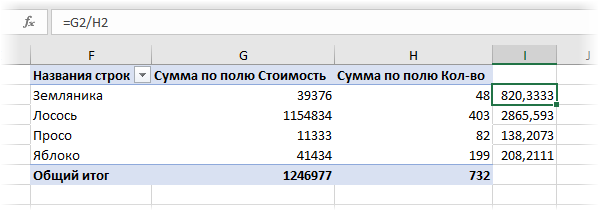
Поднимем ставки и усложним задачу. Допустим, что теперь нам нужно подсчитать средневзвешенное, но не в обычной, а в сводной таблице. Предположим, что у нас есть вот такая таблица с данными по продажам:

Заметьте, что цена на один и тот же товар может различаться. Наша задача: рассчитать средневзвешенные цены для каждого товара. Следуя той же логике, что и в предыдущем пункте, например, для земляники, которая продавалась 3 раза, это должно быть:

=(691*10 + 632*12 + 957*26)/(10+12+26) = 820,33

То есть мы суммируем стоимости всех сделок (цена каждой сделки умножается на количество по сделке) и потом делим получившееся число на общее количество этого товара.

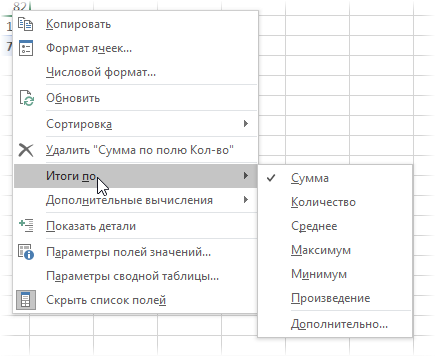
Правда, с реализацией этой нехитрой логики именно в сводной таблице нас ждет небольшой облом. Если вы работали со сводными раньше, то, наверное, помните, что можно легко переключить поле значений сводной в нужную нам функцию, щелкнув по нему правой кнопкой мыши и выбрав команду Итоги по (Summarize Values By) :

В этом списке есть среднее, но нет средневзвешенного 🙁

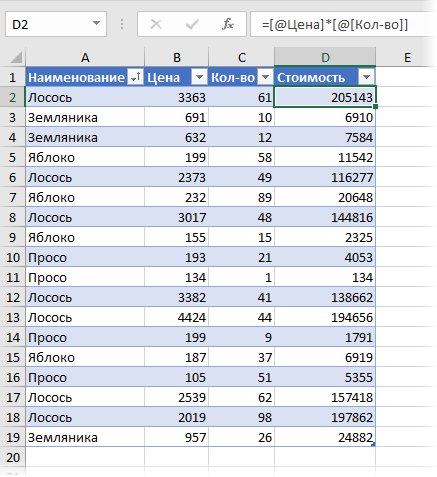
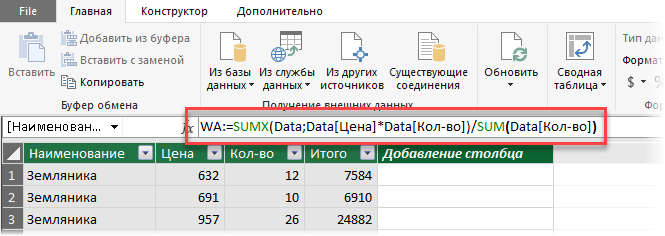
Можно частично решить проблему, если добавить в исходную таблицу вспомогательный столбец, где будет считаться стоимость каждой сделки:

В общем, как-то все неудобно, трудоемко и нагоняет тоску. Да еще и дополнительный столбец в исходных данных нужно руками делать. Но красивое решение есть.

Расчет средневзвешенного в сводной таблице с помощью Power Pivot и языка DAX

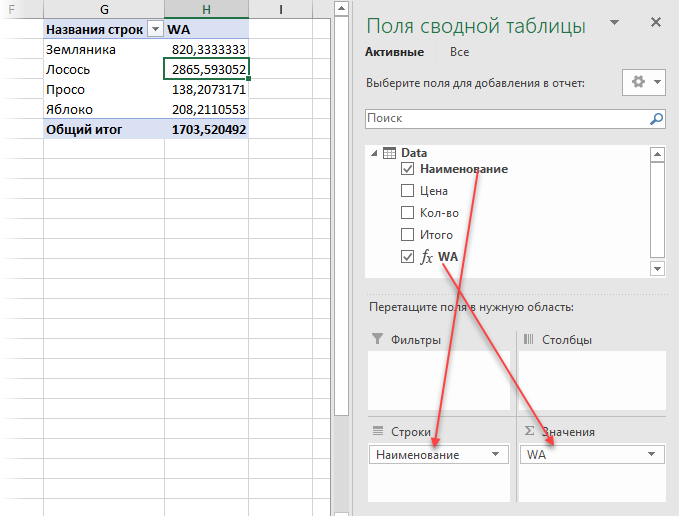
2. Затем щелкните мышью в строку формул и введите туда формулу для расчета средневзвешенного:

Несколько нюансов по формуле:

Источник

Средневзвешенное

Опубликовано 22.05.2020 · Обновлено 22.05.2021

Что такое Средневзвешенное?

Средневзвешенное значение – это расчет, который учитывает различную степень важности чисел в наборе данных. При вычислении средневзвешенного значения каждое число в наборе данных умножается на заранее определенный вес перед окончательным расчетом.

Средневзвешенное значение может быть более точным, чем простое среднее, в котором всем числам в наборе данных присваивается одинаковый вес.

Понимание средневзвешенных значений

При вычислении простого среднего или среднего арифметического все числа обрабатываются одинаково, и им присваивается одинаковый вес. Но средневзвешенное значение присваивает веса, которые заранее определяют относительную важность каждой точки данных.

Ключевые моменты

Средневзвешенное значение чаще всего вычисляется для выравнивания частоты значений в наборе данных. Например, опрос может собрать достаточно ответов от каждой возрастной группы, чтобы считаться статистически достоверным, но возрастная группа 18-34 может иметь меньше респондентов, чем все остальные, по отношению к их доле в населении. Команда опроса может взвесить результаты возрастной группы 18-34 года, чтобы их взгляды были представлены пропорционально.

Однако значения в наборе данных могут быть взвешены по другим причинам, кроме частоты появления. Например, если ученики в танцевальном классе оцениваются по навыкам, посещаемости и манерам, оценка по навыкам может иметь больший вес, чем другие факторы.

В любом случае при средневзвешенном значении каждое значение точки данных умножается на назначенный вес, который затем суммируется и делится на количество точек данных.

В средневзвешенном значении окончательное среднее число отражает относительную важность каждого наблюдения и, таким образом, является более информативным, чем простое среднее. Это также имеет эффект сглаживания данных и повышения их точности.

Взвешивание портфеля акций

Инвесторы обычно создают позицию в акции в течение нескольких лет. Это затрудняет отслеживание стоимости этих акций и их относительных изменений в стоимости.

Инвестор может рассчитать средневзвешенную цену акций, уплаченных за акции. Для этого умножьте количество акций, приобретенных по каждой цене, на эту цену, сложите эти значения и затем разделите общую стоимость на общее количество акций.

Краткая справка

Средневзвешенное значение достигается путем предварительного определения относительной важности каждой точки данных.

Например, предположим, что инвестор приобретает 100 акций компании в первый год по цене 10 долларов США и 50 акций той же компании во второй год по цене 40 долларов США. Чтобы получить средневзвешенное значение уплаченной цены, инвестор умножает 100 акций на 10 долларов для первого года и 50 акций на 40 долларов для второго года, а затем складывает результаты, чтобы получить в сумме 3000 долларов. Затем общая сумма, уплаченная за акции, в данном случае 3000 долларов, делится на количество акций, приобретенных за оба года, 150, чтобы получить средневзвешенную цену в размере 20 долларов.

Теперь это среднее значение взвешивается по количеству акций, приобретенных по каждой цене, а не только по абсолютной цене.

Примеры средневзвешенных значений

Средневзвешенные значения появляются во многих областях финансов, помимо покупной цены акций, включая доходность портфеля, учет запасов и оценку.

Когда фонд, владеющий несколькими ценными бумагами, увеличивается на 10 процентов за год, эти 10 процентов представляют собой средневзвешенную доходность фонда по отношению к стоимости каждой позиции в фонде.

Для учета запасов средневзвешенная стоимость запасов учитывает колебания цен на товары, например, в то время как методы LIFO (последний пришел – первый ушел) или FIFO (первый пришел – первый ушел) придает большее значение времени, чем стоимости.

При оценке компаний, чтобы определить, правильно ли установлена ​​цена на их акции, инвесторы используют средневзвешенную стоимость капитала (WACC) для дисконтирования денежных потоков компании. WACC взвешивается на основе рыночной стоимости долга и капитала в структуре капитала компании.

Источник

СРЕДНЕВЗВЕШЕННОЕ (СРЕДНЕЕ ЗНАЧЕНИЕ)

Смотреть что такое «СРЕДНЕВЗВЕШЕННОЕ (СРЕДНЕЕ ЗНАЧЕНИЕ)» в других словарях:

среднее значение величины — 3.14 среднее значение величины: Средневзвешенное значение величины за определенный период времени (час, сутки). Источник … Словарь-справочник терминов нормативно-технической документации

СРЕДНЕВЗВЕШЕННОЕ — (weighted average) Среднее арифметическое значение, в котором учтен вес каждого из слагаемых, для которых рассчитывается это среднее значение. Например, если кто то покупает товар тремя партиями, одна из которых – 100 тонн по 70 ф. ст. за тонну,… … Словарь бизнес-терминов

среднее — 3.3 среднее (mean): Среднее значение для (выбранного) времени усреднения результатов измерений анемометром. Источник: ГОСТ Р ИСО 1 … Словарь-справочник терминов нормативно-технической документации

средневзвешенное значение — svertinis aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted average; weighted… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

средневзвешенное значение — svertinis aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted mean vok. Gewichteter arithmetischer Mittelwert, m; gewogener Mittelwert, m; gewogenes Mittelwert, m rus.… … Fizikos terminų žodynas

средневзвешенное значение — svertinis vidurkis statusas T sritis fizika atitikmenys: angl. weighted arithmetic average; weighted average; weighted mean vok. gewogener Mittelwert, m; gewogenes Mittel, n rus. взвешенное среднее, n; средневзвешенное значение, n pranc. moyenne… … Fizikos terminų žodynas

взвешенное арифметическое среднее — svertinis aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted average; weighted… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

взвешенное среднее — svertinis aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted average; weighted… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

взвешенное арифметическое среднее — svertinis aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted mean vok. Gewichteter arithmetischer Mittelwert, m; gewogener Mittelwert, m; gewogenes Mittelwert, m rus.… … Fizikos terminų žodynas

взвешенное среднее — svertinis aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted mean vok. Gewichteter arithmetischer Mittelwert, m; gewogener Mittelwert, m; gewogenes Mittelwert, m rus.… … Fizikos terminų žodynas

Источник

Средневзвешенная формула

Формула взвешенного среднего (Содержание)

Средневзвешенная формула

Среднее арифметическое = (X1 + X2 + X3 ………. + Xn) / n

Среднее арифметическое = X1 / n + X2 / n + ………………… + Xn / n

Таким образом, все точки данных имеют одинаковый вес и задаются как 1 / n.

Но допустим, что веса различны и определяются как (w1, w2, w3 …………, wn). Таким образом, формула для средневзвешенного значения определяется как:

Weighted Mean = w1*X1 + w2*X2 + w3*X3……………+ wn*Xn

Примеры формулы взвешенного среднего (с шаблоном Excel)

Давайте рассмотрим пример, чтобы лучше понять формулу взвешенного среднего.

Допустим, у вас есть набор данных с 10 точками данных, и мы хотим рассчитать средневзвешенное значение для этого.

Набор данных: (4, 6, 8, 9, 22, 83, 98, 45, 87, 10)

Вес: (20%, 15%, 10%, 10%, 5%, 3%, 2%, 7%, 5%, 13%)

Сначала мы рассчитываем произведение набора данных и весов.

Результат будет таким, как указано ниже.

Точно так же мы рассчитали для всех данных.

Средневзвешенное значение рассчитывается по формуле, приведенной ниже

Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn

Допустим, все веса равны, т.е. 10% для каждого набора данных.

Сначала мы рассчитываем произведение набора данных и весов.

Средневзвешенное значение рассчитывается по формуле, приведенной ниже

Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn

Среднее арифметическое рассчитывается по формуле, приведенной ниже

Среднее арифметическое = (сумма всех точек данных) / количество точек данных

Поэтому, когда все веса равны, среднее арифметическое такое же, как среднее взвешенное

Допустим, у вас есть портфель, в котором у вас есть акции, облигации и товары. Таким образом, в основном у нас есть портфель, в который мы инвестировали в акции, облигации и товары. Ниже приведены веса / пропорции каждого инструмента в вашем портфеле:

Средневзвешенное значение рассчитывается по формуле, приведенной ниже

Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn

Простая средняя доходность портфеля рассчитывается по формуле, приведенной ниже

Простая средняя доходность портфеля = сумма возвратов / количество товаров

объяснение

Актуальность и использование формулы взвешенного среднего

Калькулятор формулы взвешенного среднего

Вы можете использовать следующий калькулятор взвешенного среднего

Рекомендуемые статьи

Источник