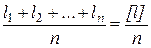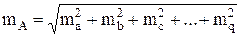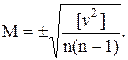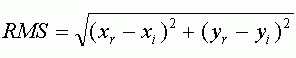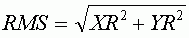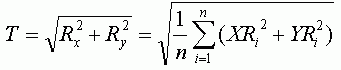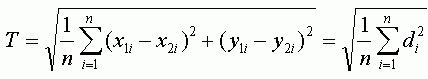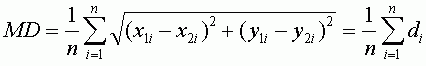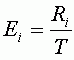что такое среднеквадратичная ошибка

Среднеквадратическая ошибка (MSE)

Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):

MSE как среднее дистанций между предсказаниями и реальными наблюдениями

Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:

MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.

Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:

Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:

Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:

$$y = 0,5252 * x + 17,306$$

Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:

Рассчитаем квадрат разницы между Y и Ỹ:

Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):

$$MSE = \frac<1> <9>× 4445 = 493$$

Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.

MSE и Scikit-learn

Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:

Инициализируем крошечные списки, содержащие реальные и предсказанные координаты y:

Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Источник

Средняя квадратичная ошибка

Оценка точности результатов измерений

Оценить точность каких-либо измерений – это значит определить на основе полученных результатов сравнимые числовые (количественные) характеристики, выражающие качественную сторону самих измерений и условий их проведения. Количественные характеристики измерений или критерии оценки точности измерений устанавливаются теорией вероятности и теорией ошибок (в частности, способом наименьших квадратов). Согласно этим теориям оценка точности результатов измерений производится только по случайным ошибкам.

Показателями точности измерений могут служить:

— средняя квадратическая ошибка измерений;

— относительная ошибка измерений;

— предельная ошибка измерений.

Понятие средней квадратичной ошибки введено Гауссом, и в настоящее время она принята в качестве основной характеристики точности измерений в геодезии.

Средней квадратичной ошибкой называется среднее квадратичное значение из суммы квадратов ошибок отдельных измерений. Для ее вычисления используют либо истинные ошибки измерений, либо уклонения результатов измерений от среднего арифметического.

Обозначим истинное значение измеряемой величины через X, результат измерения через l_i.

Истинными ошибками измерений Δ_i называются разности результатов измерений и истинных значений, т. е.

В этом случае среднюю квадратичную ошибку m отдельного результата вычисляют по формуле:

(11)

где n – количество равноточных измерений.

Однако в большинстве случаев практики, если не считать редких случаев специальных исследований, истинное значение измеряемой величины и, следовательно, истинные ошибки остаются неизвестными. В этих случаях для нахождения окончательного значения измеряемой величины и оценки точности результатов измерений используют принцип среднего арифметического.

называется средним арифметическим из измеренных значений этой величины.

Разность каждого отдельного результата измерения и среднего арифметического значения называется уклонением результатов измерений от среднего арифметического и обозначается буквой v:

v_i = l_i – .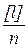

Пример. Отдельный угол измерен четырьмя приемами, и получены результаты:

Уклонения результатов измерений от среднего арифметического обладают двумя важными свойствами:

— для любого ряда равноточных измерений алгебраическая сумма уклонений равна нулю [v] = 0;

— для любого ряда равноточных измерений сумма квадратов уклонений минимальна, т. е. меньше суммы квадратов уклонений отдельных измерений от любого другого значения, принятого, вместо среднего арифметического значения, [v 2 ] = min.

Первое свойство уклонений служит надежным контролем вычисления среднего арифметического значения из результатов измерений. Второе свойство уклонений используют для оценки точности результатов измерений.

Если ошибки отдельных измерений вычисляют относительно среднего арифметического значения из результатов измерений, среднюю квадратичную ошибку отдельного результата вычисляют по формуле

. (12)

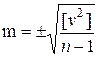
Пример. Используя данные предыдущего примера, найдем среднюю квадратичную ошибку измерения угла одним приемом:

.

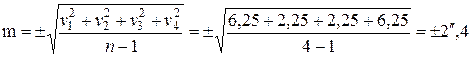
При определении средних квадратичных ошибок измерений необходимо руководствоваться следующими правилами:

;

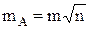
2) средняя квадратичная ошибка произведения измеренной величины на постоянное число равна произведению средней квадратичной ошибки этой величины на то же самое число, т. е. для выражения L = kl;

;

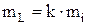
3) средняя квадратичная ошибка результатов равноточных измерений прямо пропорциональна средней квадратичной ошибке одного измерения m и обратно пропорциональна корню квадратному из числа измерений, т.е.

;

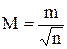
или с учетом формулы (12):

Примеры: 1. Угол β получен как разность двух направлений, определенных с ошибками m₁ = ± 3″ и m₂ = ± 4″.

По первому правилу находим .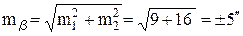

2. Радиус окружности измерен со средней квадратичной ошибкой m_R = ±5 см.

По второму правилу находим среднюю квадратичную ошибку длины окружности

m₀ = 2πm_R = 2 × 3,14 × 5 = ± 31 см.

3. Средняя квадратичная ошибка измерения угла одним приемом равно m = ± 8″. Какова точность измерения угла четырьмя приемами?

По третьему правилу

.

Источник

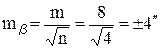
Как правильно выбрать метрику оценки для моделей машинного обучения: часть 1 Регрессионные метрики

Дата публикации Aug 26, 2018

Каждая модель машинного обучения пытается решить проблему с другой целью, используя свой набор данных, и, следовательно, важно понять контекст, прежде чем выбрать метрику. Обычно ответы на следующий вопрос помогают нам выбрать подходящий показатель:

Ну, в этом посте я буду обсуждать полезность каждой метрики ошибки в зависимости от цели и проблемы, которую мы пытаемся решить. Часть 1 фокусируется только на показателях оценки регрессии.

Метрики регрессии

Средняя квадратическая ошибка (MSE)

Это, пожалуй, самый простой и распространенный показатель для оценки регрессии, но, вероятно, наименее полезный. Определяется уравнением

гдеyᵢфактический ожидаемый результат иŷᵢэто прогноз модели.

MSE в основном измеряет среднеквадратичную ошибку наших прогнозов. Для каждой точки вычисляется квадратная разница между прогнозами и целью, а затем усредняются эти значения.

Чем выше это значение, тем хуже модель. Он никогда не бывает отрицательным, поскольку мы возводим в квадрат отдельные ошибки прогнозирования, прежде чем их суммировать, но для идеальной модели это будет ноль.

Преимущество:Полезно, если у нас есть неожиданные значения, о которых мы должны заботиться. Очень высокое или низкое значение, на которое мы должны обратить внимание.

Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсреднее значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.

Среднеквадратическая ошибка (RMSE)

Теперь очень важно понять, в каком смысле RMSE похож на MSE, и в чем разница.

Что это значит для нас?

Это означает, что, если целевым показателем является RMSE, мы все равно можем сравнивать наши модели, используя MSE, поскольку MSE упорядочит модели так же, как RMSE. Таким образом, мы можем оптимизировать MSE вместо RMSE.

На самом деле, с MSE работать немного проще, поэтому все используют MSE вместо RMSE. Также есть небольшая разница между этими двумя моделями на основе градиента.

Это означает, что путешествие по градиенту MSE эквивалентно путешествию по градиенту RMSE, но с другой скоростью потока, и скорость потока зависит от самой оценки MSE.

Таким образом, хотя RMSE и MSE действительно схожи с точки зрения оценки моделей, они не могут быть сразу взаимозаменяемыми для методов на основе градиента. Возможно, нам нужно будет настроить некоторые параметры, такие как скорость обучения.

Средняя абсолютная ошибка (MAE)

Что важно в этой метрике, так это то, что онанаказывает огромные ошибки, которые не так плохо, как MSE.Таким образом, он не так чувствителен к выбросам, как среднеквадратическая ошибка.

MAE широко используется в финансах, где ошибка в 10 долларов обычно в два раза хуже, чем ошибка в 5 долларов. С другой стороны, метрика MSE считает, что ошибка в 10 долларов в четыре раза хуже, чем ошибка в 5 долларов. MAE легче обосновать, чем RMSE.

Теперь градиент не определен, когда предсказание является совершенным, потому что, когда Y_hat равен Y, мы не можем оценить градиент. Это не определено.

Таким образом, формально, MAE не дифференцируемо, но на самом деле, как часто ваши прогнозы точно измеряют цель. Даже если они это сделают, мы можем написать простое условие IF и вернуть ноль, если это так, и через градиент в противном случае. Также известно, что вторая производная везде нулевая и не определена в нулевой точке.

Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсрединное значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.

R в квадрате (R²)

А что если я скажу вам, что MSE для моих моделей предсказаний составляет 32? Должен ли я улучшить свою модель или она достаточно хороша? Или что, если мой MSE был 0,4? На самом деле, трудно понять, хороша наша модель или нет, посмотрев на абсолютные значения MSE или RMSE. Мы, вероятно, захотим измерить, как Во многом наша модель лучше, чем постоянная базовая линия.

Когда R² отрицательно, это означает, что модель хуже, чем предсказание среднего значения.

MSE модели рассчитывается, как указано выше, в то время как MSE базовой линии определяется как:

гдеYс чертой означает среднее из наблюдаемогоyᵢ.

Чтобы сделать это более ясным, этот базовый MSE можно рассматривать как MSE, чтопростейшиймодель получит. Простейшей возможной моделью было бывсегдапредсказать среднее по всем выборкам. Значение, близкое к 1, указывает на модель с ошибкой, близкой к нулю, а значение, близкое к нулю, указывает на модель, очень близкую к базовой линии.

Распространенное заблуждение:Многие статьи в Интернете утверждают, что диапазон R² лежит между 0 и 1, что на самом деле не соответствует действительности. Максимальное значение R² равно 1, но минимальное может быть минус бесконечность.

Например, рассмотрим действительно дрянную модель, предсказывающую крайне отрицательное значение для всех наблюдений, даже если y_actual положительно. В этом случае R² будет меньше 0. Это крайне маловероятный сценарий, но возможность все еще существует.

MAE против MSE

Я заявил, что MAE более устойчив (менее чувствителен к выбросам), чем MSE, но это не значит, что всегда лучше использовать MAE. Следующие вопросы помогут вам решить:

Взять домой сообщение

В этой статье мы обсудили несколько важных метрик регрессии. Сначала мы обсудили среднеквадратичную ошибку и поняли, что наилучшей константой для нее является среднее целевое значение. Среднеквадратичная ошибка и R² очень похожи на MSE с точки зрения оптимизации. Затем мы обсудили среднюю абсолютную ошибку и когда люди предпочитают использовать MAE вместо MSE.

Спасибо за чтение, и я с нетерпением жду, чтобы услышать ваши вопросы 🙂Наслаждайтесь!

Источник

Среднеквадратичная ошибка (RMSE)

Краткая объяснение что такое RMSE применительно к данным ДЗЗ

Содержание

Введение

В случае если речь идет о привязке данных, в качестве точек между которыми измеряется расстояние могут выступать:

Как видно на иллюстрации ниже, выходные точки 1, 2, 3 поставленные оператором (синие) совпадают с трансформированными (расчетными) значениями (зеленые) и не видны из-за точного совпадения, а вот точка 4 поставлена не там, куда бы она попала используя ту же трансформацию, это дает возможность вычислить для нее RMSE, для точек 1, 2, 3 RMSE = 0.

Ошибка RMS рассчитывается по следующей формуле, представляющей из себя формулу вычисления расстояния:

RMSE выражается как расстояние в единицах исходной системы координат, то есть, если вы привязываете только что отсканированную карту, то RMSE будет выражаться в пикселях (или долях пикселя), если вы производите дополнительную привязку снимка, то RMSE будет показывать значения в метрах. Значение RMSE равное 2 для определенной точки будет означать, что ее исходная координата удалена на 2 пикселя или метра от конечной (расчетной) точки.

Чтобы лучше понять когда и как можно получить RMSE при привязке можно использовать следующий алгоритм, иллюстрирующую процесс привязки с помощью аффинного преобразования:

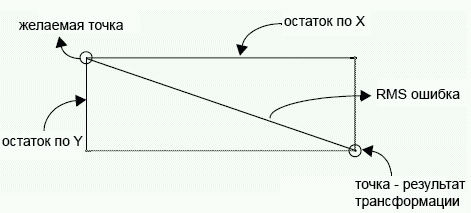
Помимо RMSE часто также можно увидеть также значения ошибки по одной из осей X или Y. Эти значения являются остатками (residuals) и могут быть рассчитаны для каждой точки. Изучение значений этих ошибок может помочь понять, почему привязанный материал смещен по одной из осей. Это проблема часто возникает при привязке данных полученных при съемке под углом (не в надир).

Уравнение вычисления RMS для каждой точки можно переписать как:

Графически ошибки по X и Y, а также RMSE соотносятся следующим образом:

Вычислив RMSE для каждой точки, можно также определить общую ошибку по X (Rx), Y (Ry) и общую RMSE (T) используя следующие формулы:

Связь со средним расстоянием

Другим, достаточно объективным, способом оценить точность привязки является среднее расстояние, которое очень похоже по формуле на RMSE, но является менее консервативным показателем, так как расстояния не возводятся в квадрат как в RMSE. Выразив расстояние через d, приведем для сравнения формулы вычисления общей RMSE (T) и среднего расстояния (MD):

RMSE является более общеупотребимым в литературе.

Другим распространенным способом описания точности набора измерений являются квантили дробные стандартному отклонению (сигма).

Вклад точки в общую RMSE

Для того, чтобы вычислить вклад точки в общую ошибку (E_i), необходимо разделить RMSE этой точки (R_i) на общую RMSE.

Допуск RMSE

В большинстве случаев, вместо того, чтобы усложнять тип трансформации (например переходить к более высоким порядкам полиномиальных преобразований) имеет смысл допустить некоторую ошибку. Величину допустимой RMSE можно представить как окно, окружающее точку с желаемыми координатами, положением расчетной точки внутри которого считается корректным. Например, если допуск RMSE равен 2, то расчетный пиксел может находится в двух пикселях от указанного оператором и являться допустимым. Величина допустимой ошибки зависит от типа и точности данных, задачи и точности контрольных точек.

Важно помнить, что RMSE указывается в пикселях, поэтому, если привязываются данные Landsat имеющие разрешение 30 метров и задача осуществить привязку с точностью не меньше тех же 30 метров, то RMSE не должна превышать 1.00 (пикселя).

Оценка RMSE

Если RMSE расчитана и найдена слишком высокой, есть 4 варианта решения проблемы:

В статье использованы материалы ERDAS IMAGINE Field Guide

Источник

Среднеквадратическая ошибка

В теории вероятностей и статистике среднеквадрати́ческое (среднеквадрати́чное) отклоне́ние — наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания (аналога среднего арифметического с бесконечным числом исходов). Обычно он означает квадратный корень из дисперсии случайной величины, но иногда может означать тот или иной вариант оценки этого значения.

Содержание

Термин [ | ]

Встречаются также синонимы словосочетания среднеквадрати́ческое отклоне́ние, как то́:

Основные сведения [ | ]

Среднеквадратическое отклонение определяется как квадратный корень из дисперсии случайной величины: σ = D [ X ] <\displaystyle \sigma =<\sqrt >> .

Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение, как и математическое ожидание, оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.

то два основных способа оценки стандартного отклонения записываются нижеследующим образом.

Оценка стандартного отклонения на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией [1] ):

Это в буквальном смысле среднее квадратическое разностей измеренных значений и среднего.

Само по себе, однако, S 0 <\displaystyle S_<0>> не является несмещённой оценкой квадратного корня из дисперсии, то есть извлечение квадратного корня «портит» несмещённость.

Среднеквадратичное отклонение среднего [ | ]

Среднее значение выборки также является случайной величиной с оценкой среднеквадратичного отклонения [2] [ нет в источнике ]

Правило трёх сигм [ | ]

Интерпретация величины среднеквадратического отклонения [ | ]

Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

Например, у нас есть три числовых множества: <0, 0, 14, 14>, <0, 6, 8, 14>и <6, 6, 8, 8>. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.

В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.

Практическое применение [ | ]

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы [ | ]

Среднее квадратическое отклонение доходности портфеля σ = D [ X ] <\displaystyle \sigma =<\sqrt >> отождествляется с риском портфеля.

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Климат [ | ]

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт [ | ]

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Пример вычисления стандартного отклонения оценок учеников [ | ]

Предположим, что интересующая нас группа (генеральная совокупность) это класс из восьми учеников, которым выставляются оценки по 10-бальной системе. Так как мы оцениваем всю группу, а не её выборку, можно использовать стандартное отклонение на основании смещённой оценки дисперсии. Для этого берём квадратный корень из среднего арифметического квадратов отклонений величин от их среднего значения.

Пусть оценки учеников класса следующие:

Тогда средняя оценка равна:

μ = 2 + 4 + 4 + 4 + 5 + 5 + 7 + 9 8 = 5 <\displaystyle \mu =<\frac <2+4+4+4+5+5+7+9><8>>=5>

Вычислим квадраты отклонений оценок учеников от их средней оценки:

( 2 − 5 ) 2 = ( − 3 ) 2 = 9 ( 5 − 5 ) 2 = 0 2 = 0 ( 4 − 5 ) 2 = ( − 1 ) 2 = 1 ( 5 − 5 ) 2 = 0 2 = 0 ( 4 − 5 ) 2 = ( − 1 ) 2 = 1 ( 7 − 5 ) 2 = 2 2 = 4 ( 4 − 5 ) 2 = ( − 1 ) 2 = 1 ( 9 − 5 ) 2 = 4 2 = 16 <\displaystyle <\begin(2-5)^<2>=(-3)^<2>=9&&(5-5)^<2>=0^<2>=0\\(4-5)^<2>=(-1)^<2>=1&&(5-5)^<2>=0^<2>=0\\(4-5)^<2>=(-1)^<2>=1&&(7-5)^<2>=2^<2>=4\\(4-5)^<2>=(-1)^<2>=1&&(9-5)^<2>=4^<2>=16\\\end>>

Среднее арифметическое этих значений называется дисперсией:

σ 2 = 9 + 1 + 1 + 1 + 0 + 0 + 4 + 16 8 = 4 <\displaystyle \sigma ^<2>=<\frac <9+1+1+1+0+0+4+16><8>>=4>

Стандартное отклонение равно квадратному корню дисперсии:

Эта формула справедлива только если эти восемь значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки восьми случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 8 нужно было бы поставить n − 1 = 7:

и стандартное отклонение равнялось бы:

Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.

Источник