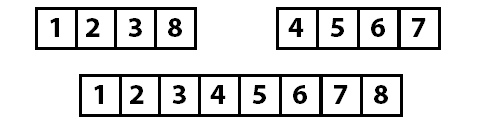
что такое сортировка массива

О сортировках (пузырьковой, быстрой, расческой. )

Эта статья ориентирована в первую очередь на начинающих программистов. О сортировках вообще и об упомянутых в заголовке в интернете море статей, зачем нужно еще одна? Например, есть хорошая статья здесь, на хабре: Пузырьковая сортировка и все-все-все. Во-первых, хорошего много не бывает, во-вторых в этой статье я хочу ответь на вопросы «зачем, что, как, почему».Зачем нужны сортировки? В первую очередь, для поиска и представления данных. Некоторые задачи с неотсортированными данными решить очень трудно, а некоторые просто невозможно. Пример: орфографический словарь, в нем слова отсортированы по алфавиту. Если бы это было не так, то попробуйте найти в нем нужное слово. Телефонная книга, где абоненты отсортированы по алфавиту. Даже если сортировка не обязательна и не сильно нужна, все равно бывает удобнее работать с отсортированными данными.

Время сортировки 100001 элемента

Измерим время сортировки для массива, содержащего 100001 элемент на компьютере с процессором Intel i5 (3.3Ггц).Время указано в сек, через дробь указано количество проходов (для быстрой сортировки оно неизвестно).Как и ожидалось, шейкерная сортировка на проблемном массиве (который полностью упорядочен, только первый и последний элементы переставлены) абсолютный лидер. Она идеально «заточена» под эти данные. Но на случайных данных сортировки расческой и qsort не оставляют соперницам шанса. Пузырьковая сортировка на проблемном массиве показывает двукратное увеличение скорости по сравнению с случайным просто потому, что количество операций перестановки на порядки меньше.

Сортировка	Простая	Пузырьковая	Шейкерная	Расчёской	Быстрая (qsort)
Стабильная	+	+	+	—	—
Случайный	23.1/100000	29.1/99585	19.8/50074	0.020/49	0.055
Проблемный	11.5/100000	12.9/100000	0.002/3	0.015/48	0.035
Обратный	18.3/100000	21.1/100000	21.1/100001	0.026/48	0.037

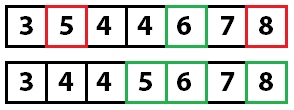
А теперь вернемся к истокам, к пузырьковой сортировке и воочию посмотрим на процесс сортировки. Видите, как на первом проходе тяжелый элемент (50) переносится в конец?

Сравниваемые элементы показаны в зеленых рамках, а переставленные — в красных

Дополнение после публикации

Я ни коей мере не считаю qsort плохой или медленной — она достаточно быстра, функциональна и при возможности следует пользоваться именно ею. Да, ей приходится тратить время на вызов функции сравнения и она уступила «расческе», которая сравнивает «по месту». Это отставание несущественно (сравните с отставанием пузырька от qsort, которое будет увеличиваться при росте массива). Пусть теперь надо сравнивать не числа, а какую-то сложную структуру по определенному полю и пусть эта структура состоит из 1000 байтов. Поместим 100тыс элементов в массив (100мб — это кое-что) и вызовем qsort. Функция fcomp (функция-компаратор) сравнит нужные поля и в результате получится отсортированный массив. При этом при перестановке элементов qsort придется 3 раза копировать фрагменты по 1000 байтов. А теперь «маленькая хитрость» — создадим массив из 100тыс ссылок на исходные элементы и передадим в qsort начало этого массива ссылок. Поскольку ссылка занимает 4 байта (в 64 битных 8), а не 1000, то при обмене ссылок qsort надо поменять эти 4/8 байтов. Разумеется, нужно будет изменить fcomp, поскольку в качестве параметров она теперь получит не адреса элементов, а адреса адресов элементов (но это несложное изменение). Зато теперь можно сделать несколько функций сортировки (каждая сортирует по своему полю структуры). И даже, при необходимости, можно сделать несколько массивов ссылок. Вот сколько возможностей дает qsort!

Кстати: использование ссылок на объекты вместо самих объектов может быть полезно не только при вызове qsort, но и при применении таких контейнеров как vector, set или map.

Источник

Алгоритмы и структуры данных для начинающих: сортировка

Авторизуйтесь

Алгоритмы и структуры данных для начинающих: сортировка

В этой части мы посмотрим на пять основных алгоритмов сортировки данных в массиве. Начнем с самого простого — сортировки пузырьком — и закончим «быстрой сортировкой» (quicksort).

Для каждого алгоритма, кроме объяснения его работы, мы также укажем его сложность по памяти и времени в наихудшем, наилучшем и среднем случае.

Метод Swap

Пузырьковая сортировка

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n)	O(n 2 )	O(n 2 )
Память	O(1)	O(1)	O(1)

Сортировка пузырьком — это самый простой алгоритм сортировки. Он проходит по массиву несколько раз, на каждом этапе перемещая самое большое значение из неотсортированных в конец массива.

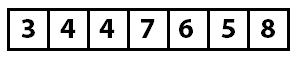
Например, у нас есть массив целых чисел:

При первом проходе по массиву мы сравниваем значения 3 и 7. Поскольку 7 больше 3, мы оставляем их как есть. После чего сравниваем 7 и 4. 4 меньше 7, поэтому мы меняем их местами, перемещая семерку на одну позицию ближе к концу массива. Теперь он выглядит так:

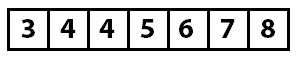
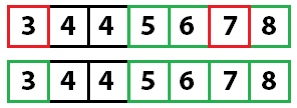
Этот процесс повторяется до тех пор, пока семерка не дойдет почти до конца массива. В конце она сравнивается с элементом 8, которое больше, а значит, обмена не происходит. После того, как мы обошли массив один раз, он выглядит так:

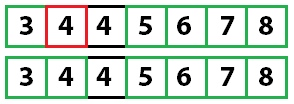
Поскольку был совершен по крайней мере один обмен значений, нам нужно пройти по массиву еще раз. В результате этого прохода мы перемещаем на место число 6.

И снова был произведен как минимум один обмен, а значит, проходим по массиву еще раз.

При следующем проходе обмена не производится, что означает, что наш массив отсортирован, и алгоритм закончил свою работу.

Сортировка вставками

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n)	O(n 2 )	O(n 2 )
Память	O(1)	O(1)	O(1)

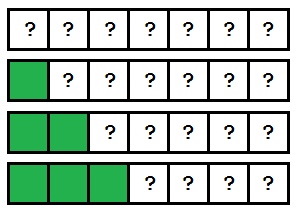
Сортировка вставками работает, проходя по массиву и перемещая нужное значение в начало массива. После того, как обработана очередная позиция, мы знаем, что все позиции до нее отсортированы, а после нее — нет.

Важный момент: сортировка вставками обрабатывает элементы массива по порядку. Поскольку алгоритм проходит по элементам слева направо, мы знаем, что все, что слева от текущего индекса — уже отсортировано. На этом рисунке показано, как увеличивается отсортированная часть массива с каждым проходом:

Постепенно отсортированная часть массива растет, и, в конце концов, массив окажется упорядоченным.

Давайте взглянем на конкретный пример. Вот наш неотсортированный массив, который мы будем использовать:

Алгоритм начинает работу с индекса 0 и значения 3. Поскольку это первый индекс, массив до него включительно считается отсортированным.

Далее мы переходим к числу 7. Поскольку 7 больше, чем любое значение в отсортированной части, мы переходим к следующему элементу.

На этом этапе элементы с индексами 0..1 отсортированы, а про элементы с индексами 2..n ничего не известно.

Итак, мы нашли индекс 1 (между значениями 3 и 7). Метод Insert осуществляет вставку, удаляя вставляемое значение из массива и сдвигая все значения, начиная с индекса для вставки, вправо. Теперь массив выглядит так:

Теперь часть массива, начиная от нулевого элемента и заканчивая элементом с индексом 2, отсортирована. Следующий проход начинается с индекса 3 и значения 4. По мере работы алгоритма мы продолжаем делать такие вставки.

Когда больше нет возможностей для вставок, массив считается полностью отсортированным, и работа алгоритма закончена.

Сортировка выбором

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n)	O(n 2 )	O(n 2 )
Память	O(1)	O(1)	O(1)

Сортировка выбором — это некий гибрид между пузырьковой и сортировкой вставками. Как и сортировка пузырьком, этот алгоритм проходит по массиву раз за разом, перемещая одно значение на правильную позицию. Однако, в отличие от пузырьковой сортировки, он выбирает наименьшее неотсортированное значение вместо наибольшего. Как и при сортировке вставками, упорядоченная часть массива расположена в начале, в то время как в пузырьковой сортировке она находится в конце.

Давайте посмотрим на работу сортировки выбором на нашем неотсортированном массиве.

При первом проходе алгоритм с помощью метода FindIndexOfSmallestFromIndex пытается найти наименьшее значение в массиве и переместить его в начало.

Имея такой маленький массив, мы сразу можем сказать, что наименьшее значение — 3, и оно уже находится на правильной позиции. На этом этапе мы знаем, что на первой позиции в массиве (индекс 0) находится самое маленькое значение, следовательно, начало массива уже отсортировано. Поэтому мы начинаем второй проход — на этот раз по индексам от 1 до n — 1.

На втором проходе мы определяем, что наименьшее значение — 4. Мы меняем его местами со вторым элементом, семеркой, после чего 4 встает на свою правильную позицию.

Теперь неотсортированная часть массива начинается с индекса 2. Она растет на один элемент при каждом проходе алгоритма. Если на каком-либо проходе мы не сделали ни одного обмена, это означает, что массив отсортирован.

После еще двух проходов алгоритм завершает свою работу:

Сортировка слиянием

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n·log n)	O(n·log n)	O(n·log n)
Память	O(n)	O(n)	O(n)

Разделяй и властвуй

До сих пор мы рассматривали линейные алгоритмы. Они используют мало дополнительной памяти, но имеют квадратичную сложность. На примере сортировки слиянием мы посмотрим на алгоритм типа «разделяй и властвуй» (divide and conquer).

Алгоритмы этого типа работают, разделяя крупную задачу на более мелкие, решаемые проще. Мы пользуемся ими каждый день. К примеру, поиск в телефонной книге — один из примеров такого алгоритма.

Если вы хотите найти человека по фамилии Петров, вы не станете искать, начиная с буквы А и переворачивая по одной странице. Вы, скорее всего, откроете книгу где-то посередине. Если попадете на букву Т, перелистнете несколько страниц назад, возможно, слишком много — до буквы О. Тогда вы пойдете вперед. Таким образом, перелистывая туда и обратно все меньшее количество страниц, вы, в конце концов, найдете нужную.

Насколько эффективны эти алгоритмы?

Предположим, что в телефонной книге 1000 страниц. Если вы открываете ее на середине, вы отбрасываете 500 страниц, в которых нет искомого человека. Если вы не попали на нужную страницу, вы выбираете правую или левую сторону и снова оставляете половину доступных вариантов. Теперь вам надо просмотреть 250 страниц. Таким образом мы делим нашу задачу пополам снова и снова и можем найти человека в телефонной книге всего за 10 просмотров. Это составляет 1% от всего количества страниц, которые нам пришлось бы просмотреть при линейном поиске.

Сортировка слиянием

При сортировке слиянием мы разделяем массив пополам до тех пор, пока каждый участок не станет длиной в один элемент. Затем эти участки возвращаются на место (сливаются) в правильном порядке.

Давайте посмотрим на такой массив:

Разделим его пополам:

И будем делить каждую часть пополам, пока не останутся части с одним элементом:

Теперь, когда мы разделили массив на максимально короткие участки, мы сливаем их в правильном порядке.

Сначала мы получаем группы по два отсортированных элемента, потом «собираем» их в группы по четыре элемента и в конце собираем все вместе в отсортированный массив.

Для работы алгоритма мы должны реализовать следующие операции:

Стоит отметить, что в отличие от линейных алгоритмов сортировки, сортировка слиянием будет делить и склеивать массив вне зависимости от того, был он отсортирован изначально или нет. Поэтому, несмотря на то, что в худшем случае он отработает быстрее, чем линейный, в лучшем случае его производительность будет ниже, чем у линейного. Поэтому сортировка слиянием — не самое лучшее решение, когда надо отсортировать частично упорядоченный массив.

Быстрая сортировка

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n·log n)	O(n·log n)	O(n 2 )
Память	O(1)	O(1)	O(1)

Быстрая сортировка — это еще один алгоритм типа «разделяй и властвуй». Он работает, рекурсивно повторяя следующие шаги:

Давайте посмотрим на работу алгоритма на следующем массиве:

Сначала мы случайным образом выбираем ключевой элемент:

Теперь, когда мы знаем ключевой индекс (4), мы берем значение, находящееся по этому индексу (6), и переносим значения в массиве так, чтобы все числа больше или равные ключевому были в правой части, а все числа меньше ключевого — в левой. Обратите внимание, что в процессе переноса значений индекс ключевого элемента может измениться (мы увидим это вскоре).

На этом этапе мы знаем, что значение 6 находится на правильной позиции. Теперь мы повторяем этот процесс для правой и левой частей массива.

Мы рекурсивно вызываем метод quicksort на каждой из частей. Ключевым элементом в левой части становится пятерка. При перемещении значений она изменит свой индекс. Главное — помнить, что нам важно именно ключевое значение, а не его индекс.

Снова применяем быструю сортировку:

У нас осталось одно неотсортированное значение, а, поскольку мы знаем, что все остальное уже отсортировано, алгоритм завершает работу.

Заключение

На этом мы заканчиваем наш цикл статей по алгоритмам и структурам данных для начинающих. За это время мы рассмотрели связные списки, динамические массивы, двоичное дерево поиска и множества с примерами кода на C#.

Источник

Основные виды сортировок и примеры их реализации

Памятка для тех, кто готовится к собеседованию на позицию разработчика

На собеседованиях будущим стажёрам-разработчикам дают задания на знание структур данных и алгоритмов — в том числе сортировок. Академия Яндекса и соавтор специализации «Искусство разработки на современном C++» Илья Шишков составили список для подготовки с методами сортировки, примерами их реализации и гифками, чтобы лучше понять, как они работают.

Пузырьковая сортировка и её улучшения

Сортировка пузырьком

Сортировка пузырьком — один из самых известных алгоритмов сортировки. Здесь нужно последовательно сравнивать значения соседних элементов и менять числа местами, если предыдущее оказывается больше последующего. Таким образом элементы с большими значениями оказываются в конце списка, а с меньшими остаются в начале.

Этот алгоритм считается учебным и почти не применяется на практике из-за низкой эффективности: он медленно работает на тестах, в которых маленькие элементы (их называют «черепахами») стоят в конце массива. Однако на нём основаны многие другие методы, например, шейкерная сортировка и сортировка расчёской.

Сортировка перемешиванием (шейкерная сортировка)

Шейкерная сортировка отличается от пузырьковой тем, что она двунаправленная: алгоритм перемещается не строго слева направо, а сначала слева направо, затем справа налево.

Сортировка расчёской

Сортировка расчёской — улучшение сортировки пузырьком. Её идея состоит в том, чтобы «устранить» элементы с небольшими значения в конце массива, которые замедляют работу алгоритма. Если при пузырьковой и шейкерной сортировках при переборе массива сравниваются соседние элементы, то при «расчёсывании» сначала берётся достаточно большое расстояние между сравниваемыми значениями, а потом оно сужается вплоть до минимального.

Первоначальный разрыв нужно выбирать не случайным образом, а с учётом специальной величины — фактора уменьшения, оптимальное значение которого равно 1,247. Сначала расстояние между элементами будет равняться размеру массива, поделённому на 1,247; на каждом последующем шаге расстояние будет снова делиться на фактор уменьшения — и так до окончания работы алгоритма.

Простые сортировки

Сортировка вставками

При сортировке вставками массив постепенно перебирается слева направо. При этом каждый последующий элемент размещается так, чтобы он оказался между ближайшими элементами с минимальным и максимальным значением.

Сортировка выбором

Сначала нужно рассмотреть подмножество массива и найти в нём максимум (или минимум). Затем выбранное значение меняют местами со значением первого неотсортированного элемента. Этот шаг нужно повторять до тех пор, пока в массиве не закончатся неотсортированные подмассивы.

Быстрая сортировка

Этот алгоритм состоит из трёх шагов. Сначала из массива нужно выбрать один элемент — его обычно называют опорным. Затем другие элементы в массиве перераспределяют так, чтобы элементы меньше опорного оказались до него, а большие или равные — после. А дальше рекурсивно применяют первые два шага к подмассивам справа и слева от опорного значения.

Быструю сортировку изобрели в 1960 году для машинного перевода: тогда словари хранились на магнитных лентах, а сортировка слов обрабатываемого текста позволяла получить переводы за один прогон ленты, без перемотки назад.

Сортировка слиянием

Сортировка слиянием пригодится для таких структур данных, в которых доступ к элементам осуществляется последовательно (например, для потоков). Здесь массив разбивается на две примерно равные части и каждая из них сортируется по отдельности. Затем два отсортированных подмассива сливаются в один.

Пирамидальная сортировка

При этой сортировке сначала строится пирамида из элементов исходного массива. Пирамида (или двоичная куча) — это способ представления элементов, при котором от каждого узла может отходить не больше двух ответвлений. А значение в родительском узле должно быть больше значений в его двух дочерних узлах.

Пирамидальная сортировка похожа на сортировку выбором, где мы сначала ищем максимальный элемент, а затем помещаем его в конец. Дальше нужно рекурсивно повторять ту же операцию для оставшихся элементов.

Источник

Сортировка

Вступление

Постановка задачи

Сортировка вставками (Сложность: \(O(N^2)\))

В качестве иллюстрации можно посмотреть видео:

Реализация алгоритма достаточно прямолинейна:

Сортировка слиянием (Сложность: \(O(N \log N)\))

Можно доказать, что не существует алгоритма сортировки, основанного на сравнениях, сложность которого меньше \(O(N \log N)\). Поэтому каждый алгоритм сравнения с такой сложностью можно назвать “оптимальным”.

Существует множество различных оптимальных алгоритмов сортировки, у каждого из которых есть свои плюсы и минусы. Более подробно к этому мы ещё вернёмся позже, но пока что перечислим самые распространённые из оптимальных алгоритмов:

Все они не настолько банальны как квадратичные алгоритмы, и требуют дополнительных знаний для анализа. Наверное, проще всего проанализировать сортировку слиянием.

Идея сортировки слиянием заключается в следующем: допустим мы знаем, что массив можно разбить на две примерно равные части, и каждая из них уже будет отсортирована. Нам нужно лишь “слить” эти две части, и мы получим отсортированный массив.

Для слияния мы создаём новый массив, изначально пустой. Затем мы параллельно идём по двум частям изначального массива, поддерживая два указателя, и на каждой итерации добавляем в новый массив меньший элемент из двух текущих, сдвигая вперёд соответствующий указатель. После добавления всех элементов из двух сливаемых частей содержание нового массива копируется в изначальный массив.

Для того, чтобы понять общую идею рекурсивных алгоритмов, лучше всего внимательно проанализировать код, приведённый ниже, или очередное иллюстративное видео:

Из фактов 1 и 2 следует что на каждом слое все слияния выполняются за \(O(N)\). Используя факт 3 видим, что сложность всего алгоритма равна \(O(N \log N)\).

И наконец, реализация алгоритма:

Стандартные алгоритмы сортировки

Стандартная библиотека любого современного языка программирования включает в себя реализацию эффективного алгоритма сортировки. Чаще всего вместо одного канонического алгоритма используется адаптивная комбинация нескольких алгоритмов: например, одна из самых распространённых реализация стандартной библиотеки C++ (libstdc++) использует комбинацию heapsort, merge sort, и insertion sort.

Для сортировки “старых” массивов используется автоматическое преобразование указателя в итератор:

Сортировка сложных типов. Собственные компараторы

Иногда в задаче требуется отсортировать не числа, а некоторые сложные объекты, состоящие из нескольких элементов. Для сортировки таких объектов чаще всего нужно вручную указывать параметр, который будет сравниваться при сортировке. Для этого и предназначены компараторы.

Приведём простой пример. Давайте сортировать результаты команд в соревновании по правилам ACM в порядке мест. То есть, место команды выше места другой команды, если она решила больше задач, или у неё меньше штраф.

Эта программа выпишет

Важно понимать, что любой компаратор \(\prec\) по сути является математическим объектом, и должен обладать несколькими важными свойствами, большинство из которых тривиальны, кроме одного: транзитивности. Компаратор является транзитивным, если из \(a \prec b\) и \(b \prec c\) следует, что \(a \prec c\). Это может казаться очевидным, но можно легко определить функцию, которая не транзитивна, и попытаться использовать её как компаратор. Математически это не имеет смысла, практически поведение std::sort в такой ситуации не определено и может стать причиной неожиданных и странных ошибок.

Понятие стабильной сортировки

Иногда от сортировки нам требуется определённое свойство: она не должна менять местами “неотличимые” элементы. Это может быть важно при сортировке сложных объектов собственными компараторами, например, в предыдущем разделе при сравнении объектов team не учитывалось поле name : две команды с одинаковым результатом считались “равными” даже если их названия не совпадали.

Стабильная сортировка гарантирует, что при наличии таких объектов в изначальном массиве, их положение относительно друг друга не изменится.

Для примера рассмотрим следующий массив объектов team :

Существует два “корректных” способа их сортировки:

Источник