что такое сопряженное пространство

Сопряжённое пространство

Сопряжённое пространство или двойственное пространство — пространство линейных функционалов на данном линейном пространстве.

Содержание

Линейно-сопряжённое пространство — определение

Пространство всех линейных функционалов, определённых на линейном пространстве , также образует линейное пространство. Это пространство называется сопряжённым к , оно обычно обозначается .

Свойства

Обозначения

Вариации и обобщения

Ссылки

Полезное

Смотреть что такое «Сопряжённое пространство» в других словарях:

Комплексно-сопряжённое пространство — Сопряжённое пространство, двойственное пространство в алгебре и функциональном анализе термин, применяющийся при описании двойственности линейных пространств. Как правило, под сопряжённым пространством понимают линейно сопряжённое пространство, т … Википедия

Пространство обобщенных функций — Обобщённая функция или распределение математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах. Понятие обобщённой функции даёт возможность выразить в… … Википедия

Пространство обобщённых функций — Обобщённая функция или распределение математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах. Понятие обобщённой функции даёт возможность выразить в… … Википедия

Двойственное пространство — Сопряжённое пространство, двойственное пространство в алгебре и функциональном анализе термин, применяющийся при описании двойственности линейных пространств. Как правило, под сопряжённым пространством понимают линейно сопряжённое пространство, т … Википедия

Векторное пространство — У этого термина существуют и другие значения, см. Пространство. Векторное (линейное) пространство основной объект изучения линейной алгебры. Содержание 1 Определение 2 Простейшие свойства … Википедия

Линейное пространство — Линейное пространство, или векторное пространство основной объект изучения линейной алгебры. Содержание 1 Определение 2 Простейшие свойства 3 Связанные определения и свойства … Википедия

Конечномерное пространство — Конечномерное пространство это векторное пространство, в котором имеется конечный базис порождающая (полная) линейно независимая система векторов. Другими словами, в таком пространстве существует конечная линейно независимая система… … Википедия

Источник

Двойственное пространство

Сопряжённое пространство, двойственное пространство в алгебре и функциональном анализе — термин, применяющийся при описании двойственности линейных пространств.

Как правило, под сопряжённым пространством понимают линейно-сопряжённое пространство, т.е. пространство линейных функционалов.

Содержание

Линейно-сопряжённое пространство — определение

Для линейных функционалов на линейном пространстве E можно определить операции сложения и умножения на число:

Свойства

Обозначения

Обычно элементы пространства E обозначают вектором-строкой, а элементы E * — вектором-столбцом. В тензорном исчислении применяется обозначение x k для элементов E (верхний, или контравариантный индекс) и x_k для элементов E * (нижний, или ковариантный индекс).

Трудности в бесконечномерном случае

Попытка прямо применить вышеприведённое определение в случае бесконечномерных линейных пространств приводит к неконструктивным и малополезным алгебраически сопряжённым пространствам. Для важного случая топологических линейных пространств рассматриваются топологически сопряжённые пространства, состоящие только из непрерывных функционалов. Однако, для топологического линейного сопряжения пространство, сопряжённое к сопряжённому, вообще говоря, с исходным не совпадает. Пространства, для которых E * * = E называются рефлексивными — только для них, строго говоря, можно употреблять термин двойственное пространство.

Комплексно-сопряжённое пространство

Термин сопряжённое пространство может иметь иное значение для линейных пространств над полем комплексных чисел: пространство 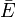, совпадающее с E как вещественное линейное пространство, но с другой структурой умножения на комплексные числа (см. en:Complex conjugate vector space):

При наличии в пространстве эрмитовой метрики (например, в гильбертовом пространстве) линейно- и комплексно-сопряжённые пространства совпадают.

См. также

Ссылки

Полезное

Смотреть что такое «Двойственное пространство» в других словарях:

Комплексно-сопряжённое пространство — Сопряжённое пространство, двойственное пространство в алгебре и функциональном анализе термин, применяющийся при описании двойственности линейных пространств. Как правило, под сопряжённым пространством понимают линейно сопряжённое пространство, т … Википедия

Нормированное векторное пространство — У этого термина существуют и другие значения, см. Пространство. В нашем пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие: Длина… … Википедия

Сопряжённое пространство — или двойственное пространство пространство линейных функционалов на данном линейном пространстве. Содержание 1 Линейно сопряжённое пространство определение 2 Свойства … Википедия

КОПСЕВДОГАЛИЛЕЕВО ПРОСТРАНСТВО — пространство, двойственное псевдогалилееву пространству. Оно является частным случаем полугиперболического пространства. Лит.:[1] Р о з е н ф е л ь д Б. А., Неевклидовы пространства, М., 1969. Л. А. Сидоров. КОПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВО… … Математическая энциклопедия

ЗАРИСКОГО КАСАТЕЛЬНОЕ ПРОСТРАНСТВО — к алгебраическому многообразию или схеме Xв точке х векторное пространство над полем вычетов (х)точки х, двойственное к пространству где максимальный идеал локального кольца О X, x точки хна X. Если и задается системой уравнений где то 3. к. п. в … Математическая энциклопедия

КО-Н-ПРОСТРАНСТВО — топологическое пространство, двойственное Н пространству … Математическая энциклопедия

УНИТАРНОЕ ПРЕДСТАВЛЕНИЕ — топологической группы представление топологич. группы унитарными операторами в гильбертовом пространстве. Теория У. п. один из наиболее разработанных разделов теории представлений топологич. групп, что связано как с его многочисленными… … Математическая энциклопедия

Источник

Комплексно-сопряжённое пространство

Сопряжённое пространство, двойственное пространство в алгебре и функциональном анализе — термин, применяющийся при описании двойственности линейных пространств.

Как правило, под сопряжённым пространством понимают линейно-сопряжённое пространство, т.е. пространство линейных функционалов.

Содержание

Линейно-сопряжённое пространство — определение

Для линейных функционалов на линейном пространстве E можно определить операции сложения и умножения на число:

Свойства

Обозначения

Обычно элементы пространства E обозначают вектором-строкой, а элементы E * — вектором-столбцом. В тензорном исчислении применяется обозначение x k для элементов E (верхний, или контравариантный индекс) и x_k для элементов E * (нижний, или ковариантный индекс).

Трудности в бесконечномерном случае

Попытка прямо применить вышеприведённое определение в случае бесконечномерных линейных пространств приводит к неконструктивным и малополезным алгебраически сопряжённым пространствам. Для важного случая топологических линейных пространств рассматриваются топологически сопряжённые пространства, состоящие только из непрерывных функционалов. Однако, для топологического линейного сопряжения пространство, сопряжённое к сопряжённому, вообще говоря, с исходным не совпадает. Пространства, для которых E * * = E называются рефлексивными — только для них, строго говоря, можно употреблять термин двойственное пространство.

Комплексно-сопряжённое пространство

Термин сопряжённое пространство может иметь иное значение для линейных пространств над полем комплексных чисел: пространство 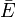, совпадающее с E как вещественное линейное пространство, но с другой структурой умножения на комплексные числа (см. en:Complex conjugate vector space):

При наличии в пространстве эрмитовой метрики (например, в гильбертовом пространстве) линейно- и комплексно-сопряжённые пространства совпадают.

См. также

Ссылки

Полезное

Смотреть что такое «Комплексно-сопряжённое пространство» в других словарях:

Сопряжённое пространство — или двойственное пространство пространство линейных функционалов на данном линейном пространстве. Содержание 1 Линейно сопряжённое пространство определение 2 Свойства … Википедия

Двойственное пространство — Сопряжённое пространство, двойственное пространство в алгебре и функциональном анализе термин, применяющийся при описании двойственности линейных пространств. Как правило, под сопряжённым пространством понимают линейно сопряжённое пространство, т … Википедия

Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия

Скалярное произведение — (в зарубежной литературе scalar product, dot product, inner product ) операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов сомножителей и угол между… … Википедия

Внутреннее произведение — определённая на векторном пространстве L над полем K симметричная эрмитова форма, рассматриваемая обычно в качестве составной части определения этого пространства[1], делающей пространство (в зависимости от типа пространства и свойств внутреннего … Википедия

Спинор — (англ. spin вращаться) специальное обобщение понятия вектора, применяемое для лучшего описания группы вращений евклидова или псевдоевклидова пространства. Смысл спинорного описания пространства V построение вспомогательного комплексного… … Википедия

КВАНТОВАЯ МЕХАНИКА — (волновая механика), теория, устанавливающая способ описания и законы движения микрочастиц (элем. ч ц, атомов, молекул, ат. ядер) и их систем (напр., кристаллов), а также связь величин, характеризующих ч цы и системы, с физ. величинами,… … Физическая энциклопедия

Кватернион — Кватернионы (от лат. quaterni, по четыре) система гиперкомплексных чисел, образующая векторное пространство размерностью четыре над полем вещественных чисел. Кватернионы минимальное расширение комплексных чисел, образующее тело,… … Википедия

Источник

СОПРЯЖЕННОЕ ПРОСТРАНСТВО

Наряду с сильной топологией, определенной нормой в Е* рассматривают и слабую *-топологию.

Лит.:[1] Райков Д. А., Векторные пространства, М., 1962.
В. И. Ломоносов.

Смотреть что такое «СОПРЯЖЕННОЕ ПРОСТРАНСТВО» в других словарях:

СОПРЯЖЕННОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ — к линейному обыкновенному дифференциальному уравнению l(y)=0 линейное обыкновенное дифференциальное уравнение где С т (I) пространство m раз непрерывно дифференцируемых комплекснозначных функций на и (черта означает операцию комплексного… … Математическая энциклопедия

ОБОБЩЕННЫХ ФУНКЦИЙ ПРОСТРАНСТВО — пространство, сопряженное к пространству основных (достаточно хороших) функций. Важную роль здесь играют Фреше пространства (типа FS )и сильно сопряженные к ним (типа DFS). Пространство типа FS есть проективный предел компактной… … Математическая энциклопедия

ЯДЕРНОЕ ПРОСТРАНСТВО — локально выпуклое пространство, у к рого все линейные непрерывные отображения в каждое банахово пространство являются ядерными операторами. Понятие Я. п. возникло [1] при исследовании вопроса о том, для каких пространств справедливы аналоги… … Математическая энциклопедия

Стереотипное пространство — В функциональном анализе и связанных областях математики стереотипные пространства представляют собой класс топологических векторных пространств, выделяемый неким специальным условием рефлексивности. Этот класс обладает серией замечательных… … Википедия

ЛОКАЛЬНО ВЫПУКЛОЕ ПРОСТРАНСТВО — отделимое топологическое векторное пространство над полем действительных или комплексных чисел, в к ром любая окрестность нулевого элемента содержит выпуклую окрестность нулевого элемента; иначе говоря, топологическое векторное пространство… … Математическая энциклопедия

МОНТЕЛЯ ПРОСТРАНСТВО — бочечное пространство (в частности, Фреше пространство), в к ром каждое замкнутое ограниченное множество компактно. Пространство всех голоморфных функций в области Gс топологией равномерной сходимости на компактах является пространством Фреше и в … Математическая энциклопедия

Источник

Дважды двойственное пространство

Почему дважды вызванный рандомный метод дважды рандомит одинаково?
Взгляните, есть метод рандомной генерации матрицы. Мы его дважды вызываем, и дважды получаем одну и.

дважды в каталоге Яндекса
сайт находится в 2-х разделах ЯК. влияет ли это на тИЦ?

Scanf не работает дважды
Вот и я решил завести аккаунт на этом форуме, т.к. часто выручает в случае каких-либо передряг и.

Дважды двойственное — это двойственное к двойственному. Линейные функционалы на линейных функционалах. Каждый вектор тоже можно рассматривать как линейный функционал на линейном функционале — каждому функционалу он ставит в соответствие значение этого функционала на самом себе, v(f) := f(v). Это соображение даёт естественное вложение векторного пространства в дважды двойственное. В конечномерном случае это естественный изоморфизм. В бесконечномерном, естественно, всё хитрее.

Капец. Я же написал, что не представляю себе что такое дважды двойственное. Какие теоремы могут быть.

Добавлено через 2 минуты
А по человечески можно объяснить ещё раз что такое двойственное к двойственному, пожалуйста. Так что б понятно было.

Добавлено через 1 минуту

Решение

Речь не про один вектор, а про пары пространств.

Значит, если у вас есть линейная форма (многочлен), у вас есть правило, по которому вы каждому набору чисел ставите в соответствие число. Это правило и есть функционал на наборах чисел.

Таким образом, можно сказать, что сопряжённое пространство есть пространство линейных форм. (С точностью до изоморфизма, но не обращайте внимания.)

Получается, что векторы исходного пространства действуют на функционалах, принадлежащих сопряжённому пространству. «Действует» значит «задаёт правило, по которому каждому функционалу ставится в соответствие число». Таким образом, векторы можно рассматривать как функционалы на функционалах, то есть как элементы второго сопряжённого. Причём других линейных функционалов на сопряжённом пространстве нет. То есть пространство векторов ― наборов чисел и линейных форм действуют друг на друге. Можно сказать, они образуют пару «равноправных» сопряжённых пространств.

Другой вариант ― можно интерпретировать как пространство векторов-столбцов, а как пространство векторов-строк, сопряжение же задаётся перемножением матриц.

Источник