что такое сложное высказывание
сложное высказывание
Смотреть что такое «сложное высказывание» в других словарях:
высказывание контрфактическое — (от лат. contra против, factum событие) сложное высказывание, в котором с помощью союза если бы. то бы. объединяются два высказывания A и В. В естественном языке ему соответствуют предложения, имеющие форму условно сослагательного наклонения … Словарь терминов логики
Высказывание (Предложение) Контрфактическое — (от лат. contra против, factum событие) а сложное высказывание, в котором с помощью союза лесли бы. то бы … Словарь терминов логики
ВЫСКАЗЫВАНИЕ — грамматически правильное повествовательное предложение, взятое вместе с выражаемым им смыслом. В логике употребляется несколько понятий В., существенно различающихся между собой. Прежде всего это понятие дескриптивного, или о п и с а тельного,… … Философская энциклопедия
Сложное синтаксическое целое (сверхфразовое единство, микротекст, период) — группа тесно взаимосвязанных законченных предложений, объединенных общностью темы в смысловой блок. Смысловые отношения, объединяющие самостоятельные предложения в С. с. ц., подкрепляются различными средствами: лексическими (повторение в… … Педагогическое речеведение
таблица истинности — таблица, с помощью которой устанавливается истинностное значение сложного высказывания при данных значениях входящих в него простых высказываний. В классической математической логике предполагается, что каждое простое (не содержащее логических… … Словарь терминов логики
ИМПЛИКАЦИЯ — [лат. implicatio сплетение, переплетение] лог. логическая операция, образующая сложное высказывание из двух высказываний посредством логической связки, соответствующей союзу «если. то. ». Словарь иностранных слов. Комлев Н.Г., 2006. импликация … Словарь иностранных слов русского языка
ИМПЛИКАЦИЯ — (от лат. implicatio сплетение, от implico тесно связываю) логическая связка, соответствующая грамматической конструкции «если. то. », с помощью которой из двух простых высказываний образуется сложное высказывание. В импликативном высказывании… … Философская энциклопедия
Сложное высказывание
Вы будете перенаправлены на Автор24
Сложное высказывание
Высказывание является одним из ключевых понятий в логике. Точного определения, которое можно было бы использовать в равной мере во всех её разделах, нет. Но можно сказать, что это повествовательное предложение, в котором что-либо утверждается или отрицается. Кроме того, про любое высказывание можно сказать, истинно оно или ложно.
Высказывание будет считаться истинным, если то, что оно описывает соответствует реальной ситуации, и ложным, если описание не соответствует ей.
Из отдельных высказываний можно разными способами выстраивать новые высказывания. Так, из высказываний «Светит солнце» и «Дует ветер» можно образовать сложные высказывания «Светит солнце и дует ветер», «Либо светит солнце, либо дует ветер «, «Если светит солнце, то дует ветер» и т.п. Сложные высказывания образуются при помощи слов «и», «либо, либо», «если, то» и т.п., которые называются логическими связками.
Высказывание является простым, если в нём в качестве своих частей нет других высказываний.
Если высказывание с помощью логических связок получено из нескольких простых высказываний, то оно называется сложным.
В математической логике определены пять основных логических операций: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность. Три первые операции являются базовыми, составляют полную систему операций, т.е. остальные могут быть нормализованы (выражены через них). В информатике обычно используются именно эти три операции.
Способы построения базовых сложных высказываний
Отрицание (инверсия)
В русском языке этой логической связке соответствует частица НЕ (иногда нужно применить оборот «неверно что. »).
Готовые работы на аналогичную тему
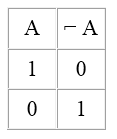
Отрицание (инверсию) можно представить в форме таблицы истинности, в которой «$1$» означает «истинно» и «$0$» – «ложно».
Конъюнкция (логическое умножение)
Если соединить два простых высказывания при помощи связки «и» («но», «а»), то получится сложное высказывание, которое называется конъюнкцией. Простые высказывания, которые соединяются таким способом, называются членами конъюнкции. Например, если высказывания «Вчера было солнечно» и «Сегодня тепло» соединить связкой «и», то получится конъюнкция «Вчера было солнечно и сегодня тепло «.
Конъюнкция истинна тогда и только тогда, когда все её составляющие являются истинными; в противном случае вся конъюнкция ложна.
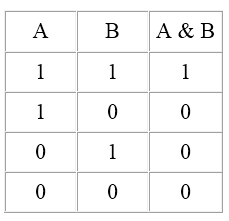
Если конъюнкцию обозначить символом «&», то таблица истинности для конъюнкции будет выглядеть следующим образом
Дизъюнкция
Для формальной логики совершенно не важен смысл простых высказываний. Достаточно знать, являются ли они истинными или ложными. Соединив два высказывания с помощью связки «или», можно получить логическое сложение (дизъюнкцию) этих высказываний. Простые высказывания, которые соединяются таким способом, называются членами дизъюнкции.
Слово «или» в обычном языке имеет два разных смысла. Оно может означать «одно или другое, или оба вместе», а может означать «одно или другое, но не оба вместе». Высказывание «Я хочу в этом сезоне пойти на «Волшебную флейту» или на «Ивана Сусанина» допускает возможность дважды посетить оперу. Высказывание «Он учится в Саратовском или в Московском университете» подразумевает, что студент учится только в одном из заявленных университетов.
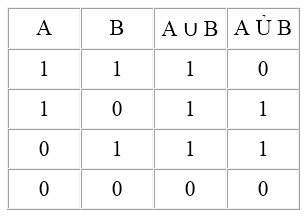
Таблица истинности для обоих видов дизъюнкции показывает, что неисключающая дизъюнкция истинна, тогда, когда истинна хотя бы одна из её составляющих; исключающая дизъюнкция истинна тогда, когда истинным является только один из ее членов, во всех остальных случаях она ложна.
Связка «или» в логике и математике всегда употребляется в неисключающем значении.
Импликация
Условное высказывание состоит из двух простых высказываний. То, что стоит за словом «если», называется предпосылкой, основанием, условием, или антецедентом (предыдущим); высказывание, которое идёт после слова «то», называется следствием, выводом, или консеквентом (последующим).
Условное высказывание в логике называется импликацией.
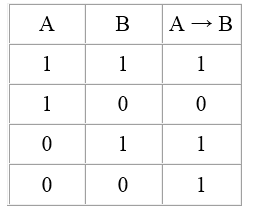
Импликация истинна в трех случаях:
когда истинны и ее основание, и ее следствие;
когда условие ложно, а следствие истинно;
когда и предпосылка, и вывод ложны.
И только в одном случае, когда условие истинно, а следствие ложно, вся импликация ложна.
Так, импликация ложна только в одном случае, когда из истинного основания следует ложный вывод.
Эквивалентность
Эквивалентность истинна тогда и только тогда, когда все составляющие ее высказывания либо ложны, либо истинны. Соответственно, эквивалентность является ложной, когда одно из входящих в нее высказываний истинно, а другое ложно.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата написания статьи: 01 04 2016
Основы алгебры логики
Основные понятия и аксиомы алгебры логики. Простые и сложные высказывания.
Исследования в алгебре логики тесно связаны с изучением высказываний, вызвано это тем, что высказывания являются одним из основных видов носителей информации. С помощью высказываний мы устанавливаем свойства, взаимосвязи между объектами.
Примерами высказываний на естественном языке являются предложения: « Сегодня светит солнце » или « На Красной площади зимой 2007–2008 гг. заливали каток ». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта. Каждое высказывание несет значение « истина » или « ложь ».
Определение. Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.
Это определение не является математически точным.
Более того, только на первый взгляд оно кажется удовлетворительным. Это определение породило много логических парадоксов.
Причина этого парадокса лежит в структуре построения указанного предложения : оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя, и, следовательно, устранены возникающие отсюда парадоксы.
Интересную задачу, содержащую парадокс, придумал знаменитый математик « Известно, что в некотором городе брадобрей бреет всех тех и только тех жителей города, которые не бреются сами. Кто бреет брадобрея? »
Определение. Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием.
Алгебра логики отвлекается от смысловой содержательности высказываний. Мы можем договориться, что абсурдное по смыслу высказывание: « Крокодилы летают » – является истинным, и с этим значением высказывания будем работать.
Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, т.е. позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания.
Употребляемые в русском языке связки « и », « или », « не », « если…, то… », « тогда и только тогда, когда … » позволяют из уже заданных высказываний строить новые, более « сложные » высказывания.
Определение. Сложное высказывание – это высказывание, которое состоит из двух или более простых высказываний, объединенных логическими связками.
В алгебре логики логическая операция полностью задается таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний, входящих в сложное высказывание.
Логические операции и соответствующие им логические связки имеют специальные названия и обозначаются следующим образом:
Что такое сложное высказывание
Простые и сложные высказывания, логические переменные и логические константы, логическое отрицание, логическое умножение, логическое сложение, таблицы истинности для логических операций
Для описания рассуждений и правил выполнения действий с информацией используют специальный язык, принятый в математической логике. В основе рассуждений содержатся специальные предложения, называемые высказываниями. В высказываниях всегда что-либо утверждается или отрицается об объектах, их свойствах и отношениях между объектами. Высказыванием является любое суждение, относительно которого можно сказать, истинно оно или ложно. Высказываниями могут быть только повествовательные предложения. Вопросительные или побудительные предложения высказываниями не являются.
Высказывание — суждение, сформулированное в виде повествовательного предложения, о котором можно сказать, истинно оно или ложно.
Например, вопросительные предложения «В каком году было первое летописное упоминание о Москве?» и «Что является внешней памятью компьютера?» или побудительное предложение «Соблюдайте правила техники безопасности в компьютерном классе» высказываниями не являются. Повествовательные предложения «Первое летописное упоминание о Москве было в 1812 г.», «Оперативное запоминающее устройство является внешней памятью компьютера» и «В компьютерном классе не надо соблюдать правила техники безопасности» являются высказываниями, поскольку это суждения, о каждом из которых можно сказать, что оно ложно. Истинными высказываниями будут суждения «Первое летописное упоминание о Москве было в 1147 г.», «Жесткий магнитный диск является внешней памятью компьютера».
Каждому высказыванию соответствует только одно из двух значений: или «истина», или «ложь», которые являются логическими константами. Истинное значение принято обозначать цифрой 1, а ложное значение — цифрой 0. Высказывания можно обозначать с помощью логических переменных, в качестве которых используются заглавные латинские буквы. Логические переменные могут принимать только одно из двух возможных значений: «истина» или «ложь». Например, высказывание «Информация в компьютере кодируется с помощью двух знаков» можно обозначить логической переменной А, а высказывание «Принтер является устройством хранения информации» можно обозначить логической переменной В. Поскольку первое высказывание соответствует действительности, то А = 1. Такая запись означает, что высказывание А истинно. Так как второе высказывание не соответствует действительности, то В = 0. Такая запись означает, что высказывание в ложно.
Высказывания могут быть простыми и сложными. Высказывание называется простым, если никакая его часть не является высказыванием. До сих пор были приведены примеры простых высказываний, которые обозначались логическими перемены ми. Выстраивая цепочку рассуждений, человек с помощью логических операций объединяет простые высказывания в сложнее’ высказывания. Чтобы узнать значение сложного высказывания нет необходимости вдумываться в его содержание. Достаточно знать значение простых высказываний, составляющих сложное высказывание, и правила выполнения логических операций.
Логическая операция — действие, позволяющее составлять сложное высказывание из простых высказываний.
Все рассуждения человека, а также работа современных технических устройств основываются на типовых действиях с информацией — трех логических операциях: логическом отрицании (инверсии), логическом умножении (конъюнкции) и логическом сложении (дизъюнкции).
Логическое отрицание простого высказывания получают добавлением слов «Неверно, что» в начале простого высказывания.
■ ПРИМЕР 1. Имеется простое высказывание «Крокодилы умеют летать». Результатом логического отрицания будет высказывание «Неверно, что крокодилы умеют летать». Значение исходного высказывания — «ложь», а значение нового — «истина».
■ ПРИМЕР 2. Имеется простое высказывание «Файл должен иметь имя». Результатом логического отрицания будет высказывание «Неверно, что файл должен иметь имя». Значение исходного высказывания — «истина», а значение нового высказывания — «ложь».
Можно заметить, что логическое отрицание высказывания истинно, когда исходное высказывание ложно, и наоборот, логическое отрицание высказывания ложно, когда исходное высказывание истинно.
Логическое отрицание (инверсия) — логическая операция, ставящая в соответствие простому высказыванию новое высказывание, значение которого противоположно значению исходного высказывания.
Обозначим простое высказывание логической переменной А. Тогда логическое отрицание этого высказывания будем обозначать НЕ А. Запишем все возможные значения логической переменной А и соответствующие результаты логического отрицания НЕ А в виде таблицы, которая называется таблицей истинности для логического отрицания (табл. 40).
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО ОТРИЦАНИЯ
Если/1 = 0, то НЕ А = 1 (см. пример 1).
Если А = 1, то НЕ А = 0 (см. пример 2)
Можно заметить, что в таблице истинности для логического отрицания ноль меняется на единицу, а единица меняется на ноль.
Логическое умножение двух простых высказываний получают объединением этих высказываний с помощью союза и. Разберем на примерах 3—6, что будет являться результатом логического умножения.
■ ПРИМЕР 3. Имеются два простых высказывания. Одно высказывание — «Карлсон живет в подвале». Другое высказывание — «Карлсон лечится мороженым».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет в подвале, и Карлсон лечится мороженым». Можно сформулировать новое высказывание более кратко: «Карлсон живет в подвале и лечится мороженым». Оба исходных высказывания ложны. Значение нового сложного высказывания также «ложь».
■ ПРИМЕР 4. Имеются два простых высказывания. Первое высказывание — «Карлсон живет в подвале». Второе высказывание — «Карлсон лечится вареньем».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет в подвале и лечится вареньем». Первое исходное высказывание ложно, а второе истинно. Значение нового сложного высказывания — «ложь».
■ ПРИМЕР 5. Имеются два простых высказывания. Первое высказывание — «Карлсон живет на крыше». Второе высказывание — «Карлсон лечится мороженым».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится мороженым». Первое исходное высказывание истин но, а второе ложно. Значение нового сложного высказывания «ложь».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится вареньем». Оба исходных высказывания истинны. Зпачение нового сложного высказывания также «истина».
Можно заметить, что логическое умножение двух высказываний истинно только в одном случае — когда оба исходных высказывания истинн ы.
Логическое умножение (конъюнкция) — логическая операция, ставящая в соответствие двум простым высказываниям новое высказывание, значение которого истинно тогда и только тогда, когда оба исходных высказывания истинны.
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО УМНОЖЕНИЯ
Логика высказываний: теория и применение. Примеры решений задач
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Логика высказываний: определение и применение
Высказываниями принято считать такие предложения (написанные на «словесном» либо математическом языке), о которых можно сказать одно из двух: либо они являются истинными, либо ложными.
С математическими высказываний проще всего: они всегда имеют либо значение «истина», либо значение «ложь». Для высказываний, сделанных на «словесном» языке, понятия «истинности» и «ложности» несколько более расплывчаты. Однако, например, такие словесные формы, как «Иди домой» и «Идёт ли дождь?», не являются высказываниями. Поэтому понятно, что высказываниями являются такие словесные формы, в которых что-либо утверждается. Не являются высказываниями вопросительные или восклицательные предложения, обращения, а также пожелания или требования. Их невозможно оценить значениями «истина» и «ложь».
Логика высказываний отвлекается от содержательной нагрузки высказываний и изучает их истинностное значение, то есть является ли высказывание истинным или ложным.
Логические операции над высказываниями
Итак, высказывания можно рассмотривать как величину, которая может принимать два значения: «истина» и «ложь».
Таблица истинности для конъюнкции:
| A | B | A ∧ B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
Таблица истинности для дизъюнкции:
| A | B | A ∨ B |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
Таблица истинности для следования (импликации):
| A | B | A → B |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
4. Четвёртая логическая операция над высказываниями, точнее над одним высказыванием, называется отрицанием высказывания A и обозначается
A (можно встретить также употребление не символа
, а символа ¬, а также верхнего надчёркивания над A).
A есть высказывание, которое ложно, когда A истинно, и истинно, когда A ложно.
Таблица истинности для отрицания:
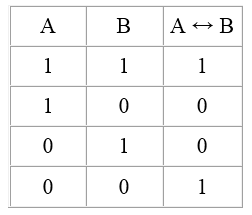
Таблица истинности для эквивалентности:
| A | B | A → B | B → A | A ↔ B |
| И | И | И | И | И |
| И | Л | Л | И | Л |
| Л | И | И | Л | Л |
| Л | Л | И | И | И |
В большинстве языков программирования есть специальные символы для обозначения логических значений высказываний, записываются они почти во всех языках как true (истина) и false (ложь).
Подытожим вышесказанное. Логика высказываний изучает связи, которые полностью определяются тем, каким образом одни высказывания строятся из других, называемых элементарными. Элементарные высказывания при этом рассматриваются как целые, не разложимые на части.
Систематизируем в таблице ниже названия, обозначения и смысл логических операций над высказываниями (они нам вскоре вновь понадобятся для решения примеров).
Для логических операций верны законы алгебры логики, которые можно использовать для упрощения логических выражений. При этом следует отметить, что в логике высказываний отвлекаются от смыслового содержания высказывания и ограничиваются рассмотрением его с той позиции, что оно либо истинно, либо ложно.
Пример 1. Вычислите логические значения следующих высказываний:
3) («Сосна» = «Дуб») ИЛИ («Вишня» = «Клён») ;
6) («Глаза даны, чтобы видеть») И («Под третьим этажом находится второй этаж») ;
Пример 2. Запишите с помощью логических операций следующие сложные высказывания:
1) «Пользователь не зарегистрирован»;
2) «Сегодня воскресенье и некоторые сотрудники находятся на работе»;
3) «Пользователь зарегистрирован тогда и только тогда, когда отправленные пользователем данные признаны годными».
Решить примеры на логику высказываний самостоятельно, а затем посмотреть решения
Пример 3. Вычислите логические значения следующих высказываний:
1) («В минуте 70 секунд») ИЛИ («Работающие часы показывают время») ;
2) (28 > 7) И (300/5 = 60) ;
4) Не((300 > 100) ИЛИ («Жажду можно утолить водой»)) ;
Пример 4. Запишите с помощью логических операций следующие сложные высказывания и вычислите их логические значения:
1) «Если часы неправильно показывают время, то можно невовремя прийти на занятия»;
Пример 5. Определите логическое значение выражения
Формулы логики высказываний
Понятие логической формы сложного высказывания уточняется с помощью понятия формулы логики высказываний.
В примерах 1 и 2 мы учились записывать с помощью логических операций сложные высказывания. Вообще-то они называются формулами логики высказываний.
Для обозначения высказываний, как и упомянутом примере, будем продолжать использовать буквы
Эти буквы будут играть роль переменных, принимающих в качестве значений истинностные значения «истина» и «ложь». Эти переменные называются также пропозициональными переменными. Мы будем далее называть их элементарными формулами или атомами.
Для построения формул логики высказываний кроме указанных выше букв используются знаки логических операций
Понятие формулы логики высказываний определим следуюшим образом:
1) элементарные формулы (атомы) являются формулами логики высказываний;
3) только те выражения являются формулами логики высказываний, для которых это следует из 1) и 2).
Определение формулы логики высказываний содержит перечисление правил образования этих формул. Согласно определению, всякая формула логики высказываний либо есть атом, либо образуется из атомов в результате последовательного применения правила 2).
1) 
2) 
3) 
4) 
5) 
6) 
1) «нет действительных чисел, которые являются рациональными»;
2) «если не все рациональные числа являются действительными, то нет рациональных чисел, являющихся действительными»;
5) «все рациональные числа являются действительными тогда и только тогда, когда не имеет место быть, что не все рациональные числа являются действительными»;
6) «не имеет места быть, что не имеет место быть, что не все рациональные числа являются действительными и нет действительных чисел, которые являются рациональными или нет рациональных чисел, которые являются действительными».
| p | q | r |  |  |  |  | f |
| И | И | И | И | И | И | И | И |
| И | И | Л | И | И | И | Л | И |
| И | Л | И | И | Л | Л | Л | Л |
| И | Л | Л | И | Л | Л | И | И |
| Л | И | И | Л | И | Л | И | И |
| Л | И | Л | Л | И | Л | И | Л |
| Л | Л | И | И | И | И | И | И |
| Л | Л | Л | И | И | И | Л | И |
Заметим, что никакой атом не имеет вида
Число скобок в формулах логики высказываний можно уменьшить, если принять, что
1) в сложной формуле будем опускать внешнюю пару скобок;
2) упорядочим знаки логических операций «по старшинству»:
В этом списке знак ↔ имеет самую большую область действия, а знак
— самую маленькую. Под областью действия знака операции понимаются те части формулы логики высказываний, к которым применяется (на которые действует) рассматриваемое вхождение этого знака. Таким образом, можно опускать во всякой формуле те пары скобок, которые можно восстановить, учитывая «порядок старшинства». А при восстановлении скобок сначала расставляются все скобки, относящиеся ко всем вхождениям знака
(при этом мы продвигаемся слева направо), затем ко всем вхождениям знака ∧ и так далее.
Пример 8. Восстановите скобки в формуле логики высказываний B ↔
Решение. Скобки восстанавливаются пошагово следующим образом:
Не всякая формула логики высказываний может быть записана без скобок. Например, в формулах А → (B → C) и
(A → B) дальнейшее исключение скобок невозможно.
Тавтологии и противоречия
Так как истинность или ложность сложных высказываний зависит лишь от значений, а не от содержания высказываний, каждому из которых соответствует определённая буква, то проверку того, является ли данное высказывание тавтологией, можно подставить следующим способом. В исследуемом выражении на место букв подставляются значения 1 и 0 (соответственно «истина» и «ложь») всеми возможными способами и с использованием логических операций вычисляются логические значения выражений. Если все эти значения равны 1, то исследуемое выражение есть тавтология, а если хотя бы одна подстановка даёт 0, то это не тавтология.
Таким образом, формула логики высказываний, которая принимает значение «истина» при любом распределении значений входящих в эту формулу атомов, называется тождественно истинной формулой или тавтологией.
Противоположный смысл имеет логическое противоречие. Если все значения высказываний равны 0, то выражение есть логическое противоречие.
Таким образом, формула логики высказываний, которая принимает значение «ложь» при любом распределении значений входящих в эту формулу атомов, называется тождественно ложной формулой или противоречием.
Кроме тавтологий и логических противоречий существуют такие формулы логики высказываний, которые не являются ни тавтологиями, ни противоречиями.
Пример 9. Составьте таблицу истинности для формулы логики высказываний 
Решение. Составляем таблицу истинности:
 |  |  |  |  |
| И | И | И | И | И |
| И | Л | Л | Л | И |
| Л | И | Л | И | И |
| Л | Л | Л | Л | И |
В значениях импликации не встречаем строку, в которой из «истины» следует «ложь». Все значения исходного высказывания равны «истине». Следовательно, данная формула логики высказываний является тавтологией.
Пример 10. Составьте таблицу истинности для формулы логики высказываний 
Решение. Составляем таблицу истинности:
 |  |  |  |  |  |
| И | И | И | И | И | И |
| И | И | Л | И | Л | Л |
| И | Л | И | Л | И | И |
| И | Л | Л | Л | Л | И |
| Л | И | И | Л | И | И |
| Л | И | Л | Л | Л | И |
| Л | Л | И | Л | И | И |
| Л | Л | Л | Л | Л | И |
Как видно ниже, таблица истинности для такой замещающей логической операции идентична таблице истинности для импликации.
 |  |  |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
Пример 11. Перепишите формулу логики высказываний 



Заменяем импликацию между двумя парами скобок, отрицая самый левый знак отрицания:

Убираем эквиваленцию между p и q и между q и не r :

Используя закон де Моргана, немного упрощаем и окончательно получаем:

Посылки и выводы. Валидный и не валидный аргумент
Пример валидного аргумента:
То есть, из посылок логически следует вывод.
Пример не валидного аргумента:
То есть, из посылок логически не следует вывод.
Пример 12. Проверьте валидность аргумента, если
Решение. Составляем таблицу истинности:
 |  |  |  |  |  |
| И | И | Л | И | И | И |
| И | Л | Л | Л | Л | И |
| Л | И | И | И | И | Л |
| Л | Л | И | И | И | И |
Применение логики высказываний в информатике и программировании
Так, может быть объявлена логическая переменная с именем «ПользовательЗарегистрирован» (или его англоязычный аналог), имеющая форму высказывания, которой может быть присвоено логическое значение «истина» при выполнении условий, что данные для регистрации отправлены пользователем и эти данные программой признаны годными. В дальнейших вычислениях значения переменных могут меняться в зависимости от того, какое логическое значение («истина» или «ложь») имеет переменная «ПользовательЗарегистрирован». В других случах переменной, например, с именем «ДоДняХОсталосьБолееТрёхДней», может быть присвоено значение «Истина» до некоторого блока вычислений, а в ходе дальнейшего исполнения программы это значение может сохраняться или меняться на «ложь» и от значения этой переменной зависит ход дальнейшего исполнения программы.
Если в программе используются несколько логических переменных, имена которых имеют форму высказываний, и из них строятся более сложные высказывания, то намного проще разрабатывать программу, если перед её разработкой записать все операции с высказываний в виде формул, применяемых в логике высказываний, чем мы в ходе этого урока и займёмся.