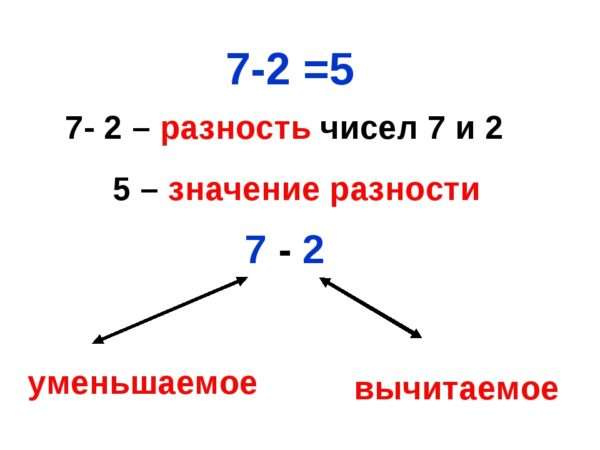
что такое слагаемое сумма разность уменьшаемое вычитаемое разность
Что такое вычитаемое уменьшаемое и разность: правило
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
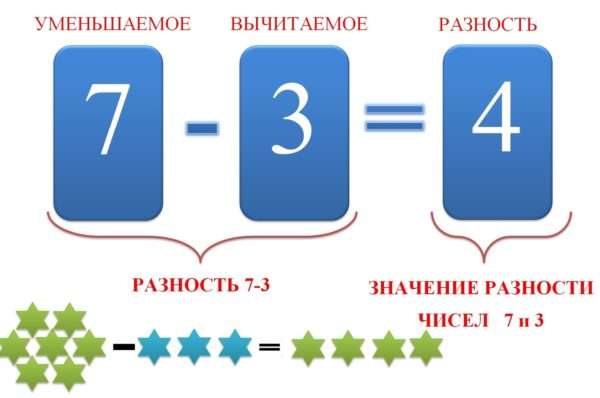
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | |
| 18 | 11 | = | 7 |
| 14 | 5 | = | 9 |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Математика. 1 класс
Конспект урока
Математика, 1 класс
Урок № 35. Уменьшаемое. Вычитаемое. Разность. Использование этих терминов при чтении записей
Перечень вопросов, рассматриваемых в теме:
Вычитание – действие обратное сложению.
Уменьшаемое – число, из которого вычитают.
Вычитаемое – число, которое вычитают.
Разность – результат вычитания.
Слагаемое – число, которое складывают.
Сумма – результат сложения.
Обязательная литература и дополнительная литература:
Теоретический материал для самостоятельного изучения
Давайте решим задачу. В гараже стояли 5 машин. 2 машины уехали. Сколько машин осталось в гараже?
Для решения задачи выберем действие вычитание. Так как машины уехали, их стало меньше.
Ответ: 3 машины в гараже.
Как называются числа при вычитании?
Первое число 8 – число, из которого вычитают. Это уменьшаемое.
Второе число 5 – число, которое вычитают. Это вычитаемое.
Третье число 3 – результат вычитания. Это разность.
Выражение 8 – 5 тоже называется разность.
Равенство 8 – 5 = 3 можно прочитать так. Уменьшаемое – 8, вычитаемое – 5. Разность – 3. Или, разность восьми и пяти равна трем.
Назовем числа при вычитании.
6 – уменьшаемое, 2 – вычитаемое, 4 – разность. Выражение 6 – 2 тоже разность.
Соединим предложение с математической записью.
Уменьшаемое – 9, вычитаемое – 6. 8 – 3
Вычитаемое – 3, уменьшаемое – 8. 7 – 2
Разность чисел 7 и 2. 9 – 6
В коробке было 10 карандашей. Взяли 4 карандаша. Сколько карандашей осталось в коробке.
Для решения задачи выберем действие вычитание. Запишем разность чисел.
Ответ: 6 карандашей.
Ответим на вопросы, поставленные в начале урока.
Числа при вычитании называются уменьшаемое, вычитаемое, разность.
Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.
Выражение на вычитание можно читать по-разному. Например, 8 – 1 = 7
Уменьшаемое – 8, вычитаемое – 1, разность – 7. Или, разность чисел 8 и 1 равна 7.
Выполним несколько тренировочных заданий.
а) Вычитаемое – 3. Уменьшаемое – 5.
б) Разность чисел 7 и 2.
в) Сумма чисел 5 и 4.
Что такое слагаемое сумма разность уменьшаемое вычитаемое разность
Тема: Слагаемые. Сумма. Уменьшаемое. Вычитаемое. Разность.
Ход урока
1. Организационное начало урока
Математика сложна,
Но скажу с почтением:
Математика нужна
Всем без исключения!
2. Актуализация знаний
1. Целеполагание
— Сегодня мы узнаем, как называются числа при сложении и вычитании. Будем решать примеры и отвечать на сказочные вопросы.
— Расставьте данные числа в порядке возрастания, чтобы узнать, в мир сказок какого писателя мы отправимся.
— А.С. Пушкин – великий русский писатель, произведения которого интересны и любимы и взрослыми, и детьми. Наш урок математики будет посвящён сказкам А. С. Пушкина, которые он написал, заложив в основу народные сказки, рассказанные ему любимой няней.
2. Устный счёт
— Сколько стихотворных сказок было написано Александром Сергеевичем?
— Правильно, пять.
— Из какой сказки эти строки?
Белка там живёт ручная,
Да затейница какая!
Белка песенки поёт
Да орешки всё грызёт.
— Попробуйте справиться со следующим заданием и «расщёлкать» цепочку примеров, как белка – золотые орешки.
– Помогите закончить следующие строчки:
Ветер по морю гуляет
И кораблик подгоняет;
Он бежит себе в волнах
На раздутых парусах.
По морю, по океану
В царство славного … Салтана.
— Молодцы! Вы должны отправить кораблики к нужному берегу.
— Царица и её сын Гвидон плыли по морю в бочке 3 дня и 3 три ночи. Сколько дней и ночей царица и её сын находились в бочке?
— Правильно, шесть. Три плюс три будет – шесть.
Я круглое и гладкое.
Но не румяное и не сладкое.
Глядят в меня,
А видят себя. (Зеркало)
— Кто из героев сказок А. С. Пушкина очень часто смотрел в зеркало?
— Правильно, царица из сказки «Сказка о мёртвой царевне и семи богатырях».
— До обеда царица смотрелась в зеркало 5 раз, а после обеда – 2раза. Сколько раз посмотрела царица в зеркало за весь день?
— Правильно, семь раз. Потому что к пяти прибавить два будет – семь.
— В лесу жили в домике 7 богатырей и одна царевна. Сколько всего человек жило в домике?
— Совершенно верно, восемь. К семи прибавить один будет – восемь.
4)
— Из каких фигур состоит иллюстрация к сказке А. С. Пушкина «Сказка о рыбаке и рыбке»?
— Домик состоит: из синего большого квадрата и жёлтого маленького квадрата, из красного большого треугольника и зелёного маленького треугольника.
Дерево состоит из зелёного овала и коричневого четырёхугольника.
Солнышко – это жёлтый круг. Пенёк – коричневый квадрат.
Физкультминутка для глаз
Глазки видят всё вокруг,
Обведу я ими круг.
Глазкам видеть всё дано:
Где окно и где крыльцо.
Обведу я снова круг,
Посмотрю на мир вокруг.
Актуализация знаний 2
3. Формирование знаний
— Сколько кораблей с белыми парусами? Шесть.
— Сколько кораблей с красными парусами? Два.
— Сколько всего кораблей? Восемь.
— Правильно.
— Число 6 – это первое слагаемое; число 2 – это второе слагаемое; число 8 – сумма.
— Запись чисел «шесть плюс два» читается: «Сумма чисел шесть и два».
Таким образом, числа, которые складываются, называются слагаемыми, а результат сложения – их суммой.
— Назовите второе слагаемое. Два.
— Найдите сумму чисел четыре и один. Сумма чисел четыре и один равна пяти.
— Назовите каждое число в этой записи математическим «именем».
— Слагаемое, слагаемое, сумма.
— Сколько рыбок поймал старик? Шесть.
— Сколько рыбок кот пытается съесть? Две.
— Правильно. Шесть минус два равно – четыре.
— В математике число шесть в таких равенствах называют уменьшаемым, число два – вычитаемым, четыре – разностью.
— Запись чисел «шесть минус два» читается: «Разность чисел шесть и два». Значит, число, которое уменьшают, называется уменьшаемым, а число, которое вычитают, называется вычитаемым. Результат является разностью.
Хоть я у всех всё отнимаю,
Но это вовсе не беда.
Я роль свою ведь выполняю,
А это, верьте, не со зла.
Поэтому вы знать должны
что компоненты все важны.
Уменьшаемое, вычитаемое, разность.
— Назовите уменьшаемое. Восемь.
— Найдите разность чисел шесть и один. Разность чисел шесть и один равна пяти.
— Назовите числа в примере их математическим «именем».
Физкультминутка
Дунул ветер – полетели.
Мы летели, мы летели
И на землю тихо сели.
Ветер снова набежал
И листочки все поднял.
Закружились, полетели
И на землю тихо сели.
Актуализация знаний 3
4. Закрепление знаний
Вдруг шатёр
Распахнулся… и девица,
Шамаханская царица,
Вся сияя, как заря,
Тихо встретила царя.
— Из какой сказки эти строки?
— Правильно, «Золотой петушок».
1)
— У Васи было три книги. Ему подарили ещё 2 книги. Сколько книг стало у Васи? Правильно, пять. Запишите этот пример. Назовите первое слагаемое –три; второе слагаемое – два; сумму – пять.
2)
-Назовите первое и второе слагаемое и запишите, сколько получится в сумме.
— Первое слагаемое – четыре, второе слагаемое два, сумма – шесть.
— Первое слагаемое – пять, второе слагаемое – три, сумма – восемь.
— Первое слагаемое – три, второе слагаемое – четыре, сумма – семь.
— Уменьшаемое равно девяти, вычитаемое – двум. Запиши разность этих чисел и вычисли её.
3)
— В море плавало восемь золотых рыбок. Одна из них уплыла. Сколько рыбок осталось?
— Верно, семь.
От восьми отнять один, будет семь.
— На ветке сидело четыре синички. К ним прилетело ещё две. Сколько птиц стало?
— Правильно, восемь. К четырём прибавить два, получится шесть.
— На полянке сидело девять зайчиков. Двое из них побежали в лес. Сколько зайчиков осталось на полянке?
— Правильно, семь. От девяти отнять два, равно семь.
Пять лодок у причала,
Волна их весело качала.
Три лодки взяли рыбаки,
Чтоб переплыть простор реки.
А сколько лодок у причала
Волна по-прежнему качала?
— Верно, две.
— От пяти отнять три равно – два.
4) Самостоятельная работа
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовиться к ЕГЭ, ОГЭ и другим экзаменам
Подготовиться к поступлению в любой ВУЗ страны
Что такое слагаемое сумма разность уменьшаемое вычитаемое разность
Числа – это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т.д.).
Для записи чисел используются специальные знаки – цифры.
1 2 3 4 5 6 7 8 9 0
Числа, которые используются при счёте, называются натуральными.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …, □
1 – самое маленькое число.
□ – самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета. Нуль не является натуральным число.
Из двух натуральных чисел больше то, которое в натуральном ряду расположено правее, а меньше то, которое расположено левее:
Из двух натуральных чисел с разным количеством разрядов больше то число, в котором разрядов больше.
Из двух натуральных чисел с одинаковым количеством разрядов больше то, у которого больше цифра старшего разряда.
45 861 47 361 47361 > 45 681
Сложение – это математическое действие.
Числа, которые складываются, называются слагаемыми.
Результат сложение называется суммой.
первое слагаемое второе слагаемое сумма
Если одно из слагаемых равно 0, сумма равна второму слагаемому:
Если оба слагаемых равны 0, то и сумма равна 0: 0 + 0 = 0
Вычитание – действие, обратное сложению.
уменьшаемое вычитаемое разность
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
Переместительный закон сложения.
От перемены мест слагаемых значение суммы не меняется:
Сочетательный закон сложения.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел или ко второму числу прибавить сумму первого и третьего чисел:
(a + b) + c = a + (b + c) = (a + c) + b
(2 + 4) + 8 = 2 + (4 + 8) = (2 + 8) + 4
Умножение – это сложение одинаковых слагаемых.
3 – число, которое показывает, сколько раз повторяется слагаемое 2 (по два три раза)
первый множитель второй множитель произведение
Деление – это действие, обратное умножению.
делимое делитель частное
Переместительный закон умножения.
От перестановки множителей произведение не меняется:
Сочетательный закон умножения.
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел или второе число умножить на произведении первого и третьего чисел:
(2 · 4) · 8 = 2 · (4 · 8) = (2 · 8) · 4
Распределительный закон умножения.
Произведение суммы на число равно сумме произведений каждого слагаемого на это число.
(a + b + c) · d = a · d + b · d + c · d
( 2 + 5 + 3 ) · 2 = 2 · 2 + 5 · 2 + 3 · 2 = 20
Чтобы умножить разность на число, достаточно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе произведение.
Чтобы разделить сумму на число, достаточно разделить каждое слагаемое на это число, а полученные результаты сложить.
Чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе частное.
Частное от деления произведений двух множителей на число равно произведению одного из множителей на частное от деления второго множителя на это число.
(a · b) : c = (a : c) · b = a · (b : c)
Чтобы разделить число на частное, достаточно разделить это число на делимое и полученный результат умножить на делитель.
Чтобы разделить частное на число, достаточно умножить делитель на это число и разделить делимое на полученный результат
Можно так же разделить делимое на это число, а полученный результат разделить на делитель.
НАХОЖДЕНИЕ КОМПОНЕНТОВ ДЕЛЕНИЯ.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
ОСОБЫЕ СЛУЧАИ УМНОЖЕНИЯ.
ОСОБЫЕ СЛУЧАИ ДЕЛЕНИЯ.
На нуль делить НЕЛЬЗЯ!
Нуль можно делить на любое число, получится 0.
На 2 делятся все чётные числа, то есть числа, которые оканчиваются цифрами 0, 2, 4, 6, 8.
На 3 делятся все числа, сумма цифр которых делится на 3.
На 5 делятся все числа, которые оканчиваются на 0 или 5.
На 6 делятся числа, которые делятся одновременно и на 2, и на 3.
На 9 делятся числа, сумма цифр которых делится на 9.
Именованные числа – это числа, полученные при измерении величин и сопровождающиеся названием единиц измерения.
Например: 2 кг, 4 см, 8 л
Именованные числа бывают простые и составные.
Простые именованные числа: 7 м, 18 т, 21 кг – в них входит только одн единица измерения.
Составные именованные числа: 2 м 4 см, 24 кг 45 г, 8 км 520 м – в них входят несколько единиц измерения.
ПРЕОБРАЗОВАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Чтобы перейти от одних единиц измерения к другим, пользуйся таблицей величин.
Единицы измерения длины
1 м = 10 дм = 100 см = 1000 мм
1 км = 1000 м = 10000 дм = 100000 см
Единицы измерения массы
1 т = 10 ц = 1000 кг
Единицы измерения времени
1 ч = 60 мин = 3600 с
1 месяц = 30 или 31 день (в феврале 28 или 29 дней)
1 год = 12 месяцев = 52 недели = 365 или 366 дней
1 век (столетие) = 100 лет
Единицы измерения площади
1 м 2 = 100 дм 2 = 10000 см 2
1 км 2 = 1000000 м 2
1 ар (1 а) = 1 сотка = 100 м 2
1 гектар (1 га) = 10000 м 2
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Складывать и вычитать можно именованные числа, выраженные в одинаковых единицах измерения.
УМНОЖЕНИЕ И ДЕЛЕНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
При умножении и делении составные именованные числа сначала заменяют простыми, а затем выполняют вычисления. В ответе простое именованное число заменяют составным.
Математическое выражение – это фраза, записанная с помощью чисел, знаков и букв.
Выражение, записанное только с помощью чисел и знаков, называется числовым.
Выражение, в котором кроме чисел и знаков есть буквы, называется буквенным.
Любое числовое выражение имеет значение. Найти значение числового выражения – значит найти его ответ.
ПОРЯДОК ДЕЙСТВИЙ В ВЫРАЖЕНИЯХ.
В выражениях без скобок, где выполняются только сложение и вычитание, действия выполняются в том порядке, в котором они записаны (то есть слева направо).
В выражениях без скобок, где выполняются только умножение и деление, действия выполняются в том порядке, в котором они записаны.
В выражениях со скобками первым выполняется действие в скобках, затем умножение или деление и только потом сложение или вычитание.
Уравнение – это равенство, которое содержит в себе неизвестное (переменную), значение которого нужно найти, чтобы равенство было верным.
Решить уравнение – значит найти все значения переменной, при которых уравнение превращается в верное равенство.
РЕШЕНИЕ ПРОСТЕЙШИХ УРАВНЕНИЙ.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, нужно к вычитаемому прибавить разность.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
УЧИМСЯ РЕШАТЬ ЗАДАЧИ.
Как работать над задачей.
1. Прочитай внимательно условие задачи и представь то, о чём идёт речь.
2. Запиши кратко задачу или сделай к ней рисунок, схему, чертёж.
3. Объясни, что означает каждое число.
4. Устно составь план решения задачи.
5. Реши задачу и найди ответ.
6. Проверь решение, составив обратную задачу.