что такое система графических координат

learnopengl. Урок 1.8 — Системы координат

Преобразование координат в нормализованные, а затем в экранные координаты обычно осуществляется пошагово, и, до окончательного преобразования в экранные координаты, мы переводим вершины объекта в несколько координатных систем. Преимущество преобразования координат через несколько промежуточных координатных систем заключается в том, что некоторые операции/вычисления проще выполняются в определённых системах, и это скоро станет очевидно. Всего есть 5 различных координатных систем, которые для нас важны:

Наши вершины будут преобразованы во все эти различные состояния, прежде чем превратятся во фрагменты.

Вероятно сейчас вы совершенно запутаны тем, что каждое пространство или координатная система из себя представляют, поэтому мы рассмотрим их в более понятном виде показав общую картину и то, что каждое из пространств действительно делает.

Общая схема

Для преобразования координат из одного пространства в другое, мы будем использовать несколько матриц трансформации, среди которых, самыми важными являются матрицы Модели, Вида и Проекции. Координаты наших вершин начинаются в локальном пространстве как локальные координаты, и в дальнейшем преобразуются в мировые координаты, потом в координаты вида, отсечения, и, наконец, все заканчивается экранными координатами. Следующее изображение показывает эту последовательность, и то, что делает каждое преобразование:

После всего этого, полученные координаты отсылаются растеризатору для превращения их во фрагменты.

Вероятно вы уже немного поняли, для чего используется каждое координатное пространство. Причина, по которой мы преобразуем наши вершины в эти различные координатные пространства, заключается в том, что некоторые операции становятся более понятными или более простыми в определенных координатных системах.

Например, модификацию вашего объекта разумнее всего выполнять в локальном пространстве, а вычисление операций учитывающих расположение других объектов лучше делать в мировых координатах, и т.д. При желании мы могли бы задать одну матрицу трансформации, которая преобразовывала координаты из локального пространства в пространство Отсечения за один шаг, но это лишит нас гибкости.

Ниже мы обсудим каждую координатную систему более подробно.

Локальное пространство

Локальное пространство это координатная система, которая является локальной для объекта, т.е. начинается в той же точке, что и сам объект. Представьте, что вы создали куб в программном пакете моделирования (подобном Blender). Начальная точка вашего куба вероятно расположена в (0,0,0), даже несмотря на то, что куб в координатах приложения может находиться в другом месте. Возможно, что все созданные вами модели имеют начальную точку (0,0,0). Следовательно, все вершины вашей модели находятся в локальном пространстве: все их координаты являются локальнми по отношению к вашему объекту.

Мировое пространство

Если мы напрямую импортируем все наши объекты в приложение, то они вероятно окажутся нагроможденными друг на друга около мировой точки отсчета (0,0,0), а это совсем не то, что мы хотим. Нам нужно определить положение каждого объекта для размещения их в более обширном пространстве. Координаты в мировом пространстве, это как раз то, о чем говорит их название: координаты всех ваших вершин относительно (игрового) мира. Это координатное пространство, в котором вы бы хотели видеть ваши объекты преобразованными таким образом, что бы они были распределены в пространстве (и желательно реалистично). Координаты вашего объекта преобразуются из локального в мировое пространство; это выполняется посредством матрицы модели.

Матрица модели это матрица, которая перемещает, масштабирует и/или вращает ваш объект для его расположения в мировом пространстве в позиции/ориентации в которой объект должен находиться. Представьте себе это как трансформацию здания, которому изменили масштаб (оно было слишком большим в локальном пространстве), перенесли его в пригород, и немного повернули влево по оси Y таким образом, что оно точно подошло к соседним домам. Вы можете воспринимать матрицу из предыдущего урока, в котором мы перемещали контейнер по сцене, как разновидность матрицы модели; с её помощью мы пересчитывали локальные координаты контейнера для размещения его в разных местах сцены/мира.

Пространство Вида

Пространство Вида это то, что люди обычно называют камерой OpenGL (иногда оно также называется пространство камеры или наблюдателя). Пространство вида это результат преобразования мировых координат в координаты, которые выглядят, как будто пользователь смотрит на них спереди. Таким образом пространство вида — это пространство видимое через видоискатель камеры. Это обычно достигается совокупностью таких сдвигов и вращений сцены, что некоторые объекты располагаются перед камерой. Эти комбинированные преобразования как правило хранятся в матрице вида, которая трансформирует мировые координаты в пространство вида. В следующем уроке мы широко обсудим, как создавать такую матрицу вида, для имитации камеры.

Пространство Отсечения

После завершения работы вершинных шейдеров, OpenGL ожидает, что все координаты будут в определенном диапазоне, а всё что выходит за его границы будет отсечено. Отсеченные координаты отбрасываются, а оставшиеся становятся фрагментами, видимыми на экране. Вот откуда пространство отсечения получило своё название.

Задавать все видимые координаты значениями из диапазона [-1.0, 1.0] на самом деле интуитивно непонятно, поэтому для работы мы определяем свой собственный набор координат и потом преобразовываем их обратно в NDC, как того ожидает OpenGL.

Обратите внимание на то, что если вне объема отсечения находится не весь примитив, например треугольник, а только его часть, то OpenGL перестроит этот треугольник в виде одного или нескольких треугольников, которые будут полностью находиться в диапазоне отсечения.

Этот объем просмотра, задаваемый матрицей проекции, называется усечённой пирамидой (frustum) и каждая координата попадающая в эту пирамиду окажется и на экране пользователя. Весь процесс конвертации координат определенного диапазона в нормализованные координаты устройства (NDC), которые могут с легкостью отображены в двумерные координаты пространства вида, называется проецирование, так как матрица проекции проецирует 3D координаты на простые-для-преобразования-в-2D нормализованные координаты устройства.

Как только координаты всех вершин будут переведены в пространство отсечения, выполняется заключительная операция, называемая перспективное деление. В ней мы делим x,y и z компоненты вектора позиции вершины на гомогенную компоненту вектора w. Перспективное деление преобразует 4D координаты пространства отсечения в трехмерные нормализованные координаты устройства. Этот шаг выполняется автоматически после завершения работы каждого вершинного шейдера.

Именно после этого этапа, полученные координаты (используя установки glViewport) отображаются на координаты экрана и превращаются во фрагменты.

Матрица проекции преобразующая координаты вида в координаты отсечения может принимать две различных формы, и каждая форма определяет свою особенную усеченную пирамиду. Мы можем создать ортографическую матрицу проекции или перспективную.

Ортографическая проекция

Матрица ортографической проекции задает усечённую пирамиду в виде параллелограмма, который является пространством отсечения, где все вершины, находящиеся вне его объема отсекаются. При создании матрицы ортографической проекции мы задаем ширину, высоту и длину видимой пирамиды отсечения. Все координаты, которые после их преобразования матрицей проекции в пространство отсечения попадают в ограниченный пирамидой объем отсечены не будут. Усеченная пирамида выглядит немного похожей на контейнер:

Усеченная пирамида определяет область видимых координат и задается шириной, высотой, ближней и дальней плоскостями. Любая координата, расположенная перед ближней плоскостью, отсекается, точно также поступают и с координатами, находящимися за задней плоскостью. Ортографическая усеченная пирамида напрямую переводит попадающие в неё координаты в нормализованные координаты устройства, и w-компоненты векторов не используются; если w-компонент равен 1.0, то перспективное деление не изменит значений координат.

Для создания матрицы ортографической проекции мы используем встроенную функцию библиотеки GLM, которая называется glm::ortho:

Первые два параметра определяют левую и правую координаты усеченной пирамиды, а третий и четвертый параметры задают нижнюю и верхнюю границы пирамиды. Эти четыре точки устанавливают размеры ближней и дальней плоскостей, а 5-й и 6-й параметры указывают расстояние между ними. Эта особая матрица проекции преобразует все координаты попадающие в диапазоны значений x, y и z, в нормализованные координаты устройства.

Ортографическая матрица проекции отображает координаты непосредственно на двумерную плоскость, которой является ваш дисплей, но в действительности, прямое проецирование дает нереалистичные результаты, потому что не принимает в расчет перспективы. Это исправляет матрица перспективной проекции.

Перспективная проекция

Если вы когда-либо наблюдали за реальным миром, то наверняка заметили, что объекты, расположенные дальше, выглядят намного меньше. Этот странный эффект мы называем перспективой. Перспектива особенно заметна, когда смотришь в конец бесконечной автомагистрали или железной дороги, как это видно на следующем изображении:

Каждый компонент координаты вершины делится на свою w-компоненту, что уменьшает значения координат пропорционально удалению от зрителя. Это еще одна причина важности w-компонента, поскольку он помогает нам с перспективной проекцией. Полученные после этого координаты находятся в нормализованном пространстве устройства. Если вам интересно разобраться, как рассчитываются ортогональные и перспективные матрицы проекции (и вы не слишком боитесь математики), то могу порекомендовать эту отличную статью Songho.

Матрицу перспективной проекции в библиотеке GLM можно создать следующим образом:

glm::perspective создает усеченную пирамиду, которая определяет видимое пространство, а все, что находится за его пределами и не попадет в объем пространства отсечения будет обрезано. Перспективная усеченная пирамида может быть представлена как коробка трапециевидной формы, каждая координата внутри которой будет отображена в точку в пространстве отсечения. Изображение перспективной усеченной пирамиды показано ниже:

Первый параметр устанавливает значение fov (field of view), что обозначает «поле обзора«, и определяет, насколько велика видимая область. Для реалистичного представления этот параметр обычно устанавливается равным 45.0f, но для получения подобия doom-стилю вы можете задавать и большие значения. Второй параметр задает соотношение сторон, которое рассчитывается путем деления ширины области просмотра на её высоту. Третий и четвертый параметры задают ближнюю и дальнюю плоскости усеченной пирамиды. Обычно мы устанавливаем ближайшее расстояние равным 0.1f, а дальнее 100.0f. Все вершины расположенные между ближней и дальней плоскостью и попадающие в объем усеченной пирамиды будут визуализированы.

Если в матрице проекции расстояние до ближней плоскости будет задано слишком большим (например, 10.0f), то OpenGL отсечет все координаты, расположенные рядом с камерой (между 0.0 и 10.0f), что дает знакомый по видео-играм визуальный эффект, когда вы можете видеть сквозь некоторые предметы если подходите к ним слишком близко.

При использовании ортогональной проекции каждая координата вершины непосредственно отображается в пространство отсечения без какого-либо мнимого перспективного деления (перспективное деление производится, но w-компонент на результат никак не влияет (он остается равен 1) и, следовательно, не имеет никакого эффекта). Поскольку ортографическая проекция не учитывает перспективу, то объекты, расположенные дальше, не кажутся меньше, что создает странное визуальное впечатление. По этой причине ортографическая проекция в основном используется для 2D-рендеринга и различных архитектурных или инженерных приложений, где мы бы предпочли отсутствие искажений, обусловленных перспективой. В таких приложениях, как Blender, предназначенных для 3D-моделирования, ортографическая проекция иногда используется во время моделирования, потому что она более точно отображает измерения и пропорции каждого объекта. Ниже приведено сравнение обоих проекционных методов в Blender:

Вы можете видеть, что при перспективной проекции удаленные вершины оказываются намного дальше, в то время как в ортографической проекции скорость удаления вершин одинаковая и не зависит от расстояния до наблюдателя.

Собираем все вместе

Создадим матрицу преобразования для каждого из вышеупомянутых шагов: модели, вида и матрицы проекции. Координата вершины преобразуется в координаты пространства отсечения следующим образом:

Обратите внимание, что порядок умножения матриц обратный (помните, что умножение матриц нужно читать справа налево). Полученная координата вершины должна быть присвоена в вершинном шейдере встроенной переменной gl_Position, после чего OpenGL автоматически выполнит перспективное деление и отсечение.

Что потом?
Координаты выходных данных вершинного шейдера должны находиться в пространстве отсечения, чего мы только что и добились с помощью матриц преобразования. OpenGL выполняет перспективное деление координат пространства отсечения, чтобы преобразовать их в нормализованные координаты устройства
Затем OpenGL использует параметры из glViewPort для сопоставления нормализованных координат устройства экранными координатами, в которых каждая координата соответствует точке на вашем экране (в нашем случае это область 800×600). Этот процесс называется преобразованием области просмотра.

Это тема трудна для понимания, поэтому, если вы все еще не совсем уверены в том, для чего используется каждое пространство, то вам не нужно беспокоиться.

Ниже вы увидите, как мы сможем эффективно применять эти координатные пространства, и в дальнейших уроках будет достаточно примеров.

Переходим к 3D

Теперь, когда мы знаем, как преобразовать 3D-координаты в 2D-координаты, мы можем начать отображать наши объекты в виде реальных 3D-объектов, а не ущербных 2D-плоскостей, которые мы показывали до сих пор.

Для начала рисования в 3D мы первым делом создадим матрицу модели. Матрица модели состоит из сдвигов, масштабирования и/или поворотов, которые мы бы хотели применить, чтобы преобразовать все вершины объекта в глобальное мировое пространство. Давайте немного изменим нашу плоскость, повернув ее по оси X, чтобы она выглядела так, будто лежит на полу. Матрица модели будет выглядеть следующим образом:

Умножив координаты вершин на эту матрицу модели мы преобразуем их в мировые координаты. Наша плоскость лежащая на полу, представляет собой таким образом плоскость в мировом пространстве.

Затем нам нужно создать матрицу вида. Чтобы объект стал видимым нам нужно немного сдвинуться в сцене назад (потому что точка зрения наблюдателя в мировом пространстве находится в начале координат (0,0,0)). Для перемещения по сцене, подумайте о следующем:

Сдвиг камеры назад — это то же самое, что перемещение всей сцены вперед.

Это именно то, что делает матрица вида: мы перемещаем всю сцену в сторону противоположную той, в которую бы мы хотели сдвинуть камеру. Так как нам нужно двигаться назад, и поскольку OpenGL использует правую систему координат, то мы должны перемещаться в положительном направлении оси z. Мы осуществляем это, сдвигая всю сцену в отрицательную сторону оси z. Это создает впечатление, что мы движемся назад.

По соглашению, OpenGL является правой координатной системой. В основном это говорит о том, что положительная ось X направлена в право от вас, положительная ось Y вверх, а положительная ось Z на вас (т.е назад). Представьте, что ваш экран является центром трех осей, и положительная ось Z проходит через экран по направлению к вам. Оси изображаются таким образом:

Чтобы понять, почему эта система называется правой, сделайте следующее:

Если вы все сделали правильно, то ваш большой палец должен указывать направление положительной оси X, указательный палец — положительную ось Y, а средний палец на положительную ось z. Если вы проделаете то же самое левой рукой, то увидите, что ось Z изменит направление. Такая система координат известна как левая и обычно используется в DirectX. Обратите внимание, что в нормализованных координатах устройства OpenGL фактически использует левую систему (матрица проекции переключает направление).

Мы обсудим перемещение по сцене более подробно в следующем уроке. На данный момент матрица вида выглядит так:

Последнее, что нам нужно определить — это матрица проекции. Для нашей сцены мы будем использовать перспективную проекцию, поэтому объявим матрицу следующим образом:

Будьте внимательны при указании градусов в GLM. Здесь мы устанавливаем параметр fov равным 45 градусам, но некоторые реализации GLM принимают fov в радианах, в этом случае вам нужно задать его как glm::radians(45.0).

Теперь, когда мы создали матрицы преобразования, мы должны передать их нашим шейдерам. Сначала давайте объявим в вершинном шейдере матрицы преобразования как uniform и умножим их на координаты вершин:

Мы также должны отправить матрицы в шейдер (обычно это делается для каждой итерации, так как матрицы преобразования имеют тенденцию часто меняться):

Теперь, когда наши координаты вершин преобразуются матрицами модели, вида и матрицей проекции, конечный объект должен:

Давайте проверим, действительно ли результат соответствует этим требованиям:

Это и правда похоже на 3D-плоскость, которая покоится на каком-то воображаемом полу. Если вы не получили такого же результата, проверьте полный исходный код, вершинный шейдер и фрагментный шейдер.

Больше 3D

До сих пор мы работали с 2D-плоскостью, но в 3D-пространстве, поэтому давайте совершим небольшое приключение и расширим нашу 2D-плоскость до 3D-куба.

Для отображения куба нам в общей сложности потребуется 36 вершин (6 сторон * по 2 треугольника * по 3 вершины в каждом). Набрать 36 вершин это довольно много, так что вы можете взять их здесь. Обратите внимание, что для получения результирующего цвета фрагментов мы будем пользоваться только текстурой, поэтому значения цвета вершин мы пропускаем.

Удаление из массива вершин атрибутов цвета меняет размер «шага» между вершинами, поэтому необходимо исправить этот параметр в вызовах функции glVertexAttribPointer:

Для разнообразия зададим кубу вращение:

И теперь нарисуем куб используя glDrawArrays, но на этот раз с количеством 36 вершин.

Вы должны получить что-то похожее на это:

Объект немного похож на куб, но что-то с ним не так. Некоторые стороны куба рисуются поверх других его сторон. Это происходит потому, что, когда OpenGL визуализирует ваш куб треугольник-за-треугольником, он перезаписывает находящиеся в буфере кадров пиксели, несмотря на его содержимое и то, что уже было нарисовано в нём до этого. Из-за этого некоторые треугольники рисуются один поверх другого, хотя они не должны перекрывать друг друга.

К счастью, OpenGL хранит информацию о глубине в буфере под названием Z-буфер, который позволяет OpenGL решить, когда рисовать поверх пикселя, а когда нет. С помощью Z-буфера, мы можем настроить OpenGL делать проверку глубины пикселей.

Z-буфер

OpenGL хранит всю информацию о глубине в Z-буфере, также известном как буфер глубины. GLFW создает это буфер автоматически (он так же имеет буфер кадра, который хранит цвета выходного изображения). Глубина хранится для каждого фрагмента (в качестве z-значения) и всякий раз, когда фрагмент выводит свой цвет, OpenGL сравнивает его значение глубины со значениями из Z-буфера, и если текущий фрагмент находится позади другого фрагмента он отбрасывается, а в противном случае перезаписывается. Этот процесс называется проверка глубины и осуществляется OpenGL автоматически.

Тем не менее, если мы хотим быть уверены в том, что OpenGL действительно выполняет проверку глубины, то сначала нам нужно её включить, потому что по-умолчанию она выключена. Включение проверки глубины осуществляется с помощью функции glEnable. Функции glEnable и glDisable позволяют включить/отключить определенные возможности OpenGL. Опции OpenGL включаются/выключаются, пока не будет сделан другой вызов функции для их отключения/включения. На данный момент мы хотим разрешить проверку глубины, включая параметр GL_DEPTH_TEST:

Так как мы используем буфер глубины, то нам нужно его очищать перед каждой итерацией визуализации (в противном случае в буфере останется информация о глубине предыдущих кадров). Мы можем очистить буфер глубины таким же образом как и буфера цвета, указав в функции glClear бит GL_DEPTH_BUFFER_BIT:

Давайте повторно запустим нашу программу и посмотрим, выполняет ли теперь OpenGL проверку глубины:

Вот и всё! Наш куб полностью текстурирован, с правильной проверкой глубины, еще и вращается. Здесь исходный код для проверки.

Больше кубиков!

Предположим, что мы хотели бы отобразить на экране 10 наших кубов. Все кубы выглядят одинаково, но будут отличаться местоположением в мировом пространстве и углом поворота. Графическое представление куба уже определено, и для того, чтобы нарисовать еще несколько объектов нам уже не нужно менять буферы или массивы атрибутов. Единственное, что мы должны исправить для каждого объекта — это его матрицу модели, благодаря которой мы преобразуем локальные координаты куба в мировые.

Во-первых, давайте определим для каждого куба вектор перемещения, который задаст положение объекта в мировом пространстве. Мы запишем 10 позиций кубов в массиве glm::vec3:

Теперь, в рамках игрового цикла мы собираемся вызвать функцию glDrawArrays 10 раз, но при этом перед каждой визуализацией будем передавать в вершинный шейдер разные матрицы модели. Мы создадим внутри игрового цикла еще один небольшой цикл, который нарисует наш объект 10 раз с разными значениями матрицы модели. Обратите внимание, что для каждого контейнера мы также добавили небольшое вращение.

Этот фрагмент кода будет обновлять матрицу модели при каждом изображении нового куба, и всего сделает это 10 раз. Сейчас мы должны видеть мир, заполненный десятью произвольно повернутыми кубами:

Отлично! Похоже, наш контейнер нашел несколько похожих на него друзей. Если вы застряли, то прежде чем продолжить посмотрите в чем может быть проблема и сравните свой код с исходным кодом, вершинным и фрагментным шейдером.

Упражнения

Источник

Система координат

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). См. географические координаты.

В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.

Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

Содержание

Список наиболее распространённых систем координат

Основные системы

В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.

Декартовы координаты

Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел :

В пространстве же необходимо уже 3 координаты :

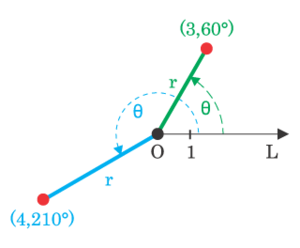
Полярные координаты

В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox.

Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат.

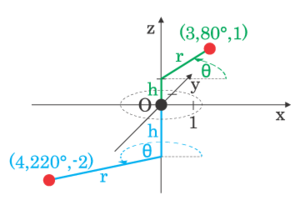
Цилиндрические координаты

Цилиндрические координаты — трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем . В терминах декартовой системы координат,

Полярные координаты имеют один недостаток: значение θ теряет смысл, если r = 0.

Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение , тогда как в цилиндрических оно выглядит как r = c

Сферические координаты

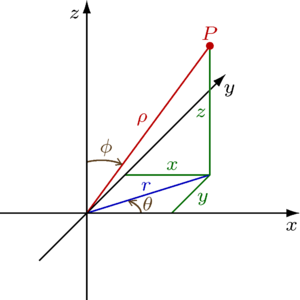
Сферические координаты — трехмерный аналог полярных

Обозначения, принятые в Америке

В сферической системе координат, расположение точки P определяется тремя компонентами: . В терминах декартовой системы координат,

Сферическая система координат также имеет недостаток: φ теряет смысл если ρ = 0, также и θ теряет смысл, если ρ = 0 или φ = 0 или φ = 180°.

Для построения точки по её сферическими координатами, нужно: от полюса отложить отрезок, равный ρ вдоль положительной z-оси, вернуть его на угол φ вокруг оси y в направлении положительной x-оси, и вернуть на угол θ вокруг z-оси в направлении положительной y-оси.

Сферические координаты полезны при изучении систем, симметричных вокруг точки. Так, уравнение сферы в декартовых координатах выглядит как , тогда как в сферических становится намного проще: .

Европейские обозначения

В Европе принято использовать другие обозначения. Положение точки задаётся числами: , Где r — расстояние от точки до начала координат, — полярный угол, который изменяется в пределах от 0 до π, — Азимутальный угол, который изменяется в пределах от 0 до 2π. То есть, в европейской системе, которая применяется также и в России, обозначения для углов переставлены по сравнению с американской.

Переход из одной системы координат в другую

Декартовы и полярные

Источник