что такое симметрия в математике 3 класс примеры фигур
Презентация к уроку по математике в 3 классе. Тема «Симметрия»
Описание презентации по отдельным слайдам:
Математика З класс Плахотная Инна Петровна учитель начальных классов МОУ СОШ №5 г.Гусев
КТО ДУМАЕТ, ТОТ ВСЕГДА ДОДУМАЕТСЯ
Симметрия При перегибании половинки фигур совпадают (способ наложения) Что это такое? Как строить? Где встречается? З Н А Е М ХОТИМ УЗНАТЬ
Симметрия – соразмерность, одинаковость в расположении частей чего-нибудь, по противоположным сторонам от точки, прямой или плоскости
Середина отрезка AB, соединяющего симметричные точки, лежит на оси симметрии. Условия симметрии
Условия симметрии Отрезок AB, соединяющий симметричные точки, перпендикулярен оси симметрии. Середина отрезка AB, соединяющего симметричные точки, лежит на оси симметрии.
О симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю Ты в Эйфелевой башне, в бабочке и мошке, Ты в елочке, что у лесной дорожки. С тобою в дружбе Гусевский вокзал И наша школа – знаний капитал. Середина отрезка AB, соединяющего симметричные точки, лежит на оси симметрии. Отрезок AB, соединяющий симметричные точки, перпендикулярен оси симметрии.
«Симметрия … есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство» Г.Вейль
Архитектурные памятники Петровский дворец
Архитектурные памятники Собор в Милане
Архитектурные памятники Макет Эйфелевой башни в городе Гусеве
Архитектурные памятники Храм Христа Спасителя
Архитектурные памятники Собор Парижской Богоматери
Дом офицеров в городе Гусеве Архитектурные памятники
Архитектурные памятники Берлинский кафедральный собор
Архитектурные памятники Кремль. Москва
Максимова Т.В., Целоусова Т.Ю. Поурочные разработки по математике. 3 класс. – М.: ВАКО, 2004. Петерсон Л.Г. Математика. 3 класс. – М.: Баласс, 2004. http://www.gifpark.ru/index.html http://images.yandex.ru/
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Скоростное чтение
Курс повышения квалификации
Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО
Ищем педагогов в команду «Инфоурок»
Презентация к уроку по теме «Симметрия» для 3 класса.
Цели:
· Познакомить с симметрией как преобразованием фигур на плоскости.
· Изучить закономерности расположения симметричных точек и фигур, учить строить симметричные фигуры.
· Повторить материал о перпендикулярных линиях, вертикальных и горизонтальных.
Оборудование:
· Проектор, экран, компьютер.
· Карточки для индивидуальной работы, листы нелинованной бумаги.
· Чертежные инструменты: линейки, угольники, карандаши я 3 класса.
Номер материала: 112795
Не нашли то что искали?
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
ОНФ проверит качество охраны в российских школах
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
В России стартовал прием заявок на конкурс для журналистов-школьников «Медиабум»
Время чтения: 2 минуты
Школьники из России выиграли 8 медалей на Международном турнире по информатике
Время чтения: 3 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
К 2024 году в каждой российской школе должен появиться спортивный клуб
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Математика (3-й класс). Симметрия
Класс: 3
Познакомить с симметрией как преобразованием фигур на плоскости; изучить закономерности расположения симметричных точек и фигур; учить строить симметричные фигуры.
Развитие математической речи, мышления, внимания, воображения, памяти, умения работать в группе и самостоятельно.
1) мультимедийное оборудование;
2) экран;
3) компьютер;
4) диск с презентацией урока;
5) чистые листы для практической работы;
6) циркули для практической работы;
7) рисунки к задаче № 3;
8) рисунки к задаче № 4;
9) опоры для нахождения площади и периметра прямоугольника;
10) квадратики для творческого задания, листы бумаги, клей;
11) электронная игра
Ход урока
I. Организационный момент
Настрой учащихся на работу. Дети разделены на 4 группы.
II. Устный счёт
Работа проводится с использованием компьютера, мультимедийного проектора и электронной игры.
– Разложи карточки с верными ответами:
Ответы: 7, 8, 30, 70, 200, 300, 400, 500, 600, 4000, 6000, 9000.
III. Постановка проблемы:
– Назовите цифры, из которых составлены числа ответов.
Запись на доске: 0,2,3,4,5,6,7,8,9.
– Есть ли среди этих цифр симметричные? Какие? (0,8)
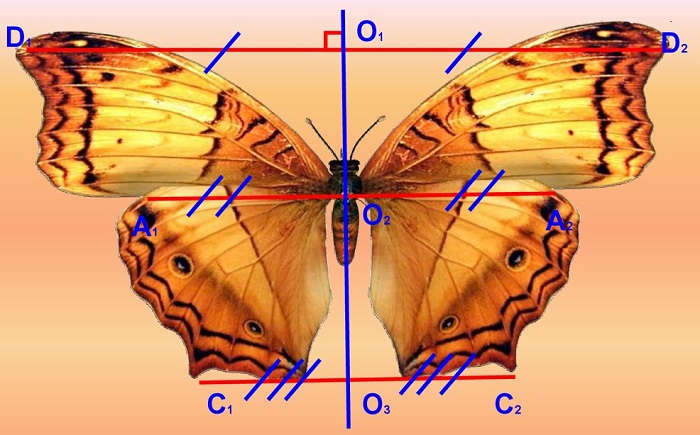
– Можно ли сказать, что фигура бабочки симметрична? А фигура собачки? (Работа по 1 слайду презентации)
IV. Постановка темы и цели урока:
– Что такое симметрия? Дома вы должны были прочитать и выписать из толкового словаря, что означает это слово.
(Соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости). (Работа по 2 слайду презентации)
– Тема нашего урока Симметрия.
– А какова цель урока? (Научиться определять симметричные фигуры и строить их на плоскости).
V. Работа по теме:
1. Практическая работа: (Работа по 3 слайду презентации):
– Нам надо на чистом листе бумаги обозначить 2 симметричные точки А и В. Как это сделать?
а) – Сложите пополам лист бумаги и проколите его ножкой циркуля. Разверните лист.
У вас получились 2 точки. Обозначим их А и В, а линию сгиба прямой L. В математике прямую L называют осью симметрии.
– Что интересного заметили в расположении точек А и В?
б) – Соедините точки А и В отрезком. Точку пересечения этого отрезка с прямой L обозначьте буквой О.
– Измерьте отрезки АО и ВО. Что можете о них сказать? (АО=ВО)
– Значит, точка О делит отрезок АВ на равные части. Отсюда следует, что АО=ВО.
Выводится 1 свойство.
в) – Теперь возьмём угольник и приложим к углу, который образуется отрезком АВ и осью симметрии.
– Какой угол получили? (Прямой)
– Прямые, образующие прямой угол называются перпендикулярными.
Выводится 2 свойство.
г) – А теперь, опираясь на доску, сформулируйте свойство симметричных точек.
(Симметричные точки расположены на прямой, перпендикулярной оси симметрии, на равном расстоянии от неё).
2. Работа по учебнику (с. 40):
– Откройте учебники на с. 40 и прочитаем текст во второй рамке.
VI. Первичное закрепление:
Проверка: объясняют с места, опираясь на опору на доске (3 слайд).
№ 3. (с. 41). Коллективно у доски и в учебниках.
VII. Работа над пройденным.
(Работа по 4 слайду презентации)
1. Игра “Роботы”: (в тетрадях самостоятельно)
– По данной программе нарисуйте фигуру.
– Дорисуйте вторую половину фигуры так, чтобы она была симметрична первой.
– Проверьте, такая ли фигура у вас получилась? (на слайде появляется фигура)
2. Нахождение периметра и площади данной фигуры:
– Как найти периметр и площадь данной фигуры, если её стороны имеют такую длину. (Работа по 5 слайду презентации)
– Как найти периметр фигуры? Как рациональней это сделать? (Работа по 6 слайду презентации)
3. Составление симметричного узора (Работа в группах):
– Составьте из данных фигур симметричный узор.
– Как определить ось симметрии? (Согнуть лист)
VIII. Итог
(Работа по 7 слайду презентации)
Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.
Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.
Что такое симметрия
Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.
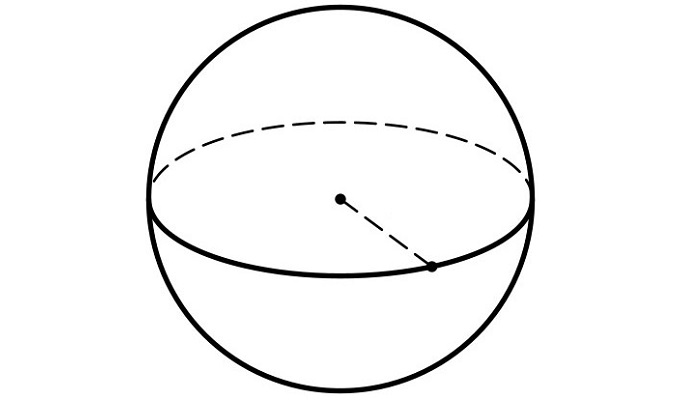
В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.
Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.
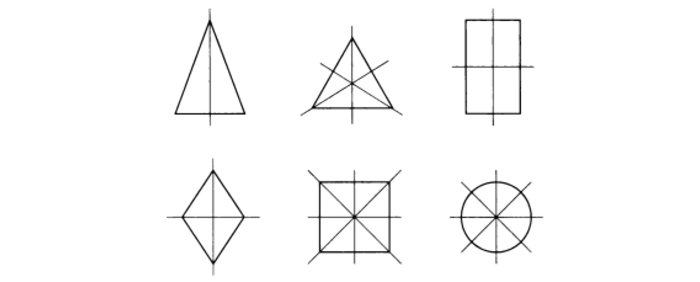
Рис. 1 Фигуры, обладающие симметричностью
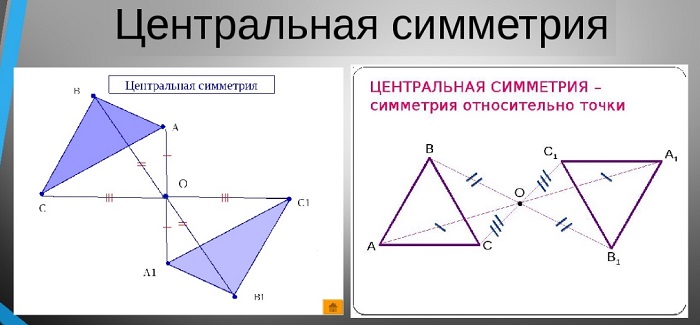
Центральная симметрия
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.
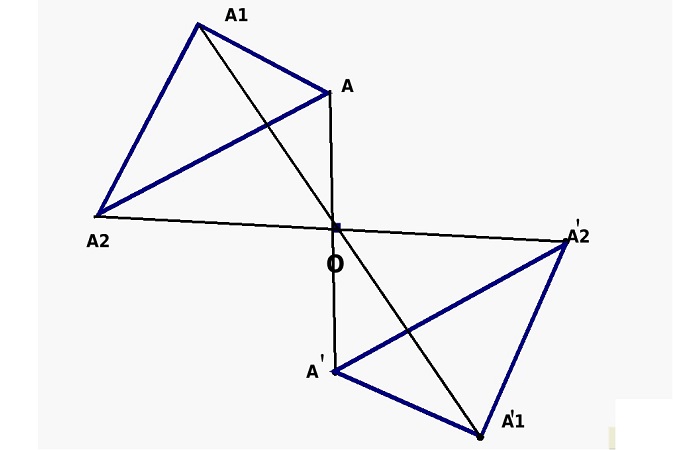
Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.
Рис. 2 Графическое представление центральной симметрии
Осевая симметрия
Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.
Рис. 3 Наглядное представление осевой симметрии
В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.
Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.
Рис. 4 Примеры осевой симметрии
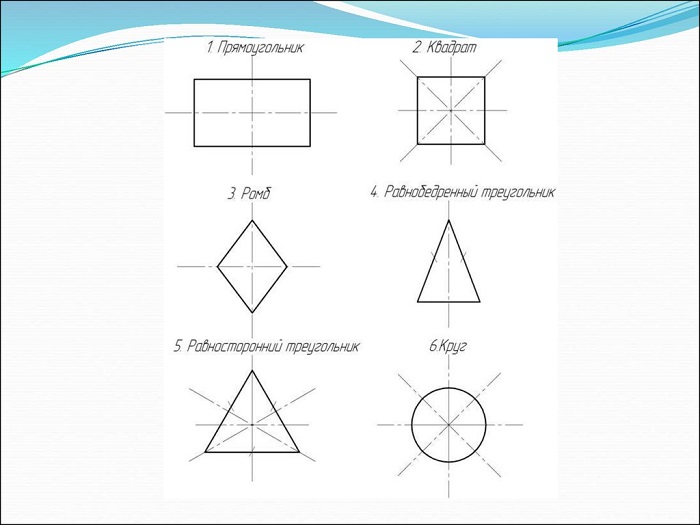
Фигуры, имеющие несколько осей симметрии
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
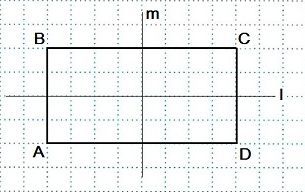
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.
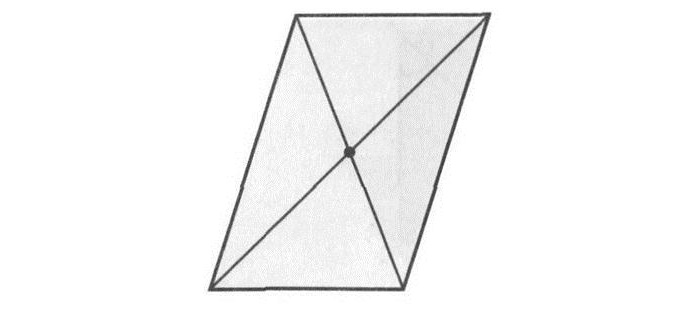
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.
Рис. 5 Оси симметрии ромба
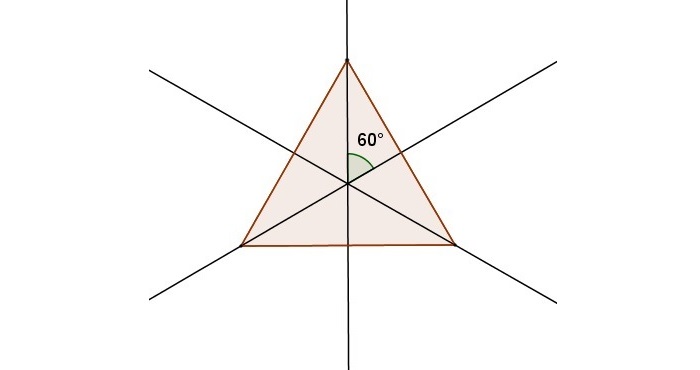
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.
Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.
Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
Осевая и центральная симметрия
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 2. Постройте треугольник A1B1C1, симметричный треугольнику ABC, относительно центра (точки О).
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
«Симметричные и несимметричные фигуры» 3 класс математика
Выбранный для просмотра документ урок-презентация.pptx
Описание презентации по отдельным слайдам:
Урок математики 3 класс по теме : «Симметричные и несимметричные плоские фигуры» Подготовила учитель начальных классов КГУ «Фрунзенская средняя школа» Бортвина Ю.И.
Итог урока. Что нового узнали на уроке? Какие бывают предметы и геометрические фигуры? Что такое симметрия? Как называется линия, которая делит предметы на ровные половины? Что такое ассиметрия? Где в природе встречается симметрия? Где в жизни встречается симметрия?
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-458625
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Минобрнауки планирует учредить стипендию для студентов-философов
Время чтения: 2 минуты
Отказавшихся от вакцинации сотрудников МГУ отстранили от работы со студентами
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
ОНФ проверит качество охраны в российских школах
Время чтения: 2 минуты
Только каждый 10-й россиянин может дать платное образование своим детям
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.