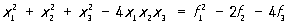что такое симметричная функция

СИММЕТРИЧЕСКАЯ ФУНКЦИЯ

цифры в десятичной записи суммы произвольного количества одноразрядных чисел, «функция голосования», к-рая характеризуется тем, что ее аргументы принимают лишь два значения: 1 («за») и 0 («против»), а сама функция равна 1, если больше половины ее аргументов равны 1, и 0 в противном случае. Тривиальными примерами С. ф. являются константы и функция одной переменной.

или правенств вида

К С. ф. относятся симметрические многочлены. Всякая рациональная С. ф. (над полем характеристики 0) является отношением двух симметрич. многочленов. Любая булева С. ф. на наборах значений аргументов, содержащих одинаковое число единиц, принимает одинаковые значения. Эти функции играют важную роль в математич. кибернетике и ее приложениях, в частности они встречаются при схемной реализации арифметических и нек-рых других операций.

Лит.:[1] В а в дер Варден Б. Л., Алгебра, пер. с нем., 2 изд., М., 1979; [2] Яблонский С. В., Введение в дискретную математику, М., 1979. В. М. Храпченко.

Полезное

Смотреть что такое «СИММЕТРИЧЕСКАЯ ФУНКЦИЯ» в других словарях:

симметрическая функция — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN symmetric function … Справочник технического переводчика

симметрическая функция — simetrinė funkcija statusas T sritis fizika atitikmenys: angl. symmetric function vok. symmetrische Funktion, f rus. симметрическая функция, f pranc. fonction symétrique, f … Fizikos terminų žodynas

СИММЕТРИЧЕСКАЯ ПРОИЗВОДНАЯ — обобщение понятия производной на случай функций множества Ф в n мерном евклидовом пространстве. С. п. в точке хесть предел где S(х; r) замкнутый шар с центром в точке хи радиусом r. С. п. порядка nв точке хфункции действительного переменного f(х) … Математическая энциклопедия

СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — порядка пв точке хфункции действительного переменного f(x) выражение Часто также симметрич. разностью называют выражение получающееся из вышеприведенного заменой hна 2h. Если функция f(x).имеет в точке хпроизводную fn (х).порядка п, то Т. П.… … Математическая энциклопедия

Кососимметрическая функция — Кососимметрическая (или знакопеременная) функция функция от нескольких переменных, не меняющаяся при чётных перестановках аргументов и меняющая знак при нечётных перестановках. Например, следующие функции являются кососимметрическими, так как они … Википедия

Знакопеременная функция — Кососимметрическая (или знакопеременная) функция функция от нескольких переменных, не меняющаяся при чётных перестановках аргументов и меняющая знак при нечётных перестановках. Например следующие функции являются кососимметрическими, так как они… … Википедия

Знакопеременная функция — такое выражение, зависящее от нескольких количеств, которое изменяет только знак, а не величину, при замене одного из этих количеств другим. Напр. у х, у3 х3, lg(x/y) и т. п. Если f(x,у) есть симметрическая функция переменных х и у, то φ(x,у) =… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Рекурсивная функция (теория вычислимости) — У этого термина существуют и другие значения, см. Рекурсивная функция (значения). Термин рекурсивная функция в теории вычислимости используется для обозначения трёх классов функций примитивно рекурсивные функции; общерекурсивные функции; … Википедия

Примитивно рекурсивная функция — Термин рекурсивные функции в теории вычислимости используют для обозначения трёх множеств функций примитивно рекурсивные функции; общерекурсивные функции; частично рекурсивные функции. Последние совпадают с множеством вычислимых по Тьюрингу… … Википедия

Частично рекурсивная функция — Термин рекурсивные функции в теории вычислимости используют для обозначения трёх множеств функций примитивно рекурсивные функции; общерекурсивные функции; частично рекурсивные функции. Последние совпадают с множеством вычислимых по Тьюрингу… … Википедия

Источник

Симметрические функции

Полезное

Смотреть что такое «Симметрические функции» в других словарях:

Симметрические функции — Функция от n переменных х1, x2. хn наз. симметрическою, если она не меняется при всевозможных перестановках этих переменных. Например: x12x2 + x12x3 + х22×1 + x22x3 + x32x1+ x32x2 есть С. функция, так как она не меняется при всех… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Альтернативные функции — суть такие функции от двух или нескольких переменных величин, которые при перестановке двух входящих в них переменных изменяют только свой знак, но не свою абсолютную величину (симметрические же функции в этом случае сохраняют как то, так и… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

БОЛЬШИХ ЧИСЕЛ ЗАКОН — общий принцип, в силу к рого совместное действие случайных факторов приводит при нек рых весьма общих условиях к результату, почти не зависящему от случая. Сближение частоты наступления случайного события с его вероятностью при возрастании числа… … Математическая энциклопедия

Комбинаторика — (Комбинаторный анализ) раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими… … Википедия

Разбиение числа — n это представление n в виде суммы положительных целых чисел, называемых частями. При этом порядок следования частей не учитывается (в отличие от композиций), то есть разбиения, отличающиеся только порядком частей, считаются равными. В… … Википедия

Перечисление (комбинаторика) — У этого термина существуют и другие значения, см. Перечисление. В комбинаторике под перечислением понимается подсчёт количества или непосредственное построение и перебор всех объектов заданного типа. Раздел комбинаторики, изучающий задачи… … Википедия

Варинг Эдуард — Варинг, Уэринг (Waring) Эдуард (1734, Олд Хит, близ Шрусбери, ‒ 15.8.1798, Плили в Понтсбери), английский математик. Профессор Кембриджского университета (с 1760), член Лондонского королевского общества (1763). Основные труды ‒ по алгебре… … Большая советская энциклопедия

Варинг — Уэринг (Waring) Эдуард (1734, Олд Хит, близ Шрусбери, 15.8.1798, Плили в Понтсбери), английский математик. Профессор Кембриджского университета (с 1760), член Лондонского королевского общества (1763). Основные труды по алгебре… … Большая советская энциклопедия

ГАУССА ТЕОРЕМА — (theorema egregium): гауссова кривизна (произведение главных кривизн) регулярной поверхности в евклидовом пространстве не меняется при изгибаниях поверхности. (Здесь регулярность означает гладкое погружение.) Г. т. следует из того, что гауссова… … Математическая энциклопедия

Тифлисская физическая обсерватория — Тифлисская обсерватория Здание обсерватории во вто … Википедия

Источник

Симметричные функции.

Disclamer: Эти рассказы не претендуют на уровень исследований. Это просто рассказы о том, как я заметил когда-то давно закономерность и «поиграл» с ней.

Когда не было калькуляторов, все пользовались для умножения логарифмическими линейками. Исходный принцип этого метода крайне прост: чтобы посчитать произведение чисел a и b, можно посчитать их логарифмы — ln(a) и ln(b), сложить и узнать, логарифмом какого числа является результат.
ab = exp(ln(a) + ln(b))
или наоборот:
a + b = ln( exp(a) + exp(b) )

Когда я узнал об этом замечательном факте, мне сразу пришла в голову мысль: а не может ли быть так, что любые «достаточно благоразумные» симметричные функции можно выразить через сумму или произведение? Пусть s(x,y) = s(y,x), тогда существуют такие функции перехода f и g, что
s(x,y) = f( g(x) + g(y) )
или соотв.
s(x,y) = f( g(x) · g(y) )

А может, чего доброго, это работает не только для сложения-умножения, я для любой симметричной функции вообще? Т.е. между двумя любыми симметричными функциями n аргументов существуют переходные функции. Пусть у нас есть две n-аргументных симметричных ф-ции. Первую будем обозначать a * b * ··· * d, вторую обозначим a × b × ··· × d. (Это не имеет сейчас никакой связи с умножением, просто обозначения.) Если эти функции удовлетворяют определённым условиям «благоразумности», которые мы найдём позже, то существуют функции f и g, такие, что:
a * b * ··· * d = g( f(a) × f(b) × ··· × f(d) )

Вначале посмотрим, как обстоят дела с натуральными числами.
Попытаемся представить произвольную симметричную функцию n аргументов через сумму.

Если функция симметрична, значит ей не нужно знать, в каком порядке шли её аргументы. Ей нужно только знать, какие числа среди них содержались и в каком количестве.
s(1,2,2) можно посчитать, зная только что среди аргументов была одна единица и две двойки. Объект, хранящий информацию о содерщащихся в нём объектах и их количестве называется мультимножеством. Будем обозначать мультимножество, получаемое из последовательности (1,2,2) символом [1,2,2]. Пока что мы вывели следующее правило: функция s(x,y,z) тогда и только тогда симметрична, когда существует функция S: S[x,y,z] = s(x,y,z).

Любой человек, хоть раз програмировавший, знает, что еденицами и нулями (точнее, их последовательностями) можно закодировать почти всё, что угодно. 🙂 Уж конечные мультимножества — точно. Вот мы и попробуем. Пусть функция k кодирует мультимножества натуральными числами, а K их декодирует. Вот бы здорово было, если бы k[a] + k[b] + k[c] = k[a, b, c]! Тогда решение было бы у нас в кармане.
s(x,y,z) = S[x,y,z] = S°K°k[x,y,z] = S°K(k[x] + k[y] + k[z])

Вот мы и выразили симметричную функцию через сумму!
Осталось только найти нужную функцию K, но это как раз очень просто. Для n-аргументной функции будем кодировать k[x] как (n+1)^x. Если рассматривать запись этого числа в (n+1)-ичной системе счисления, это будет единица на x-той позиции. Складывая k[x] и k[y] получаем единицу в x-той и единицу в y-позиции, либо двойку в x-той позиции, если числа равны. Таким образом, из полученной суммы всегда можно восстановить информацию, какие числа в нашем мультимножестве содержатся и в каком количестве. Ичность системы счисления — (n+1) — гарантирует, что не случится перескока в высший разряд. У нашей функции же всего n-аргументов. Даже если все они будут одинаковыми, мы получим всего лишь цифру n в соответствующем разряде.

Для выражения через умножение можно кодировать простыми числами. k[x] = p_x (x-тое простое число). При умножение степени разны простых чисел не интерферируют, а одинаковых — складываются. Так что, мы сможем добыть из произведения информацию обо всех числах, которые в него входили.

Обратим внимание, что наш чудный метод работает не только для натуральных чисел, но вообще для всех счётных множеств, содержащих таковые. Чтобы показать это, нужно просто добавить в k дополнительный этап кодирования, преобразующий x в натуральное число. В часности, наш результат верен для рациональных чисел. Если наша функция отображает из рациональных чисел в действительные, это всё-равно работает! Действительно, мы нигде не говорили о том, куда функция отображает, нас интересовало только то, откуда. Этот факт может помочь нам при изучении непрерывных симметричных функций, ведь каждая непрерывная функция однозначно задаётся своим ограничением на рациональные числа.

С действительными числами можно выполнить аналогичный финт ушами. Через Аксиому Выбора можно доказать, что у действительных чисел есть базис над рациональными. Т.н. базис Гимеля. Счётностью этот базис, разумеется, не отличается. Если бы он был счётным, множество действительных чисел было бы равномощно множеству конечных последовательностей рациональных => счётно.

А раз базис Гимеля имеет ту же мощность, что и сами действительные числа, значит существует биекция между ними. Вот и будем кодировать каждое действительное число соответствующим ему вектором в базисе. При суммировании компоненты разных базисных векторов не интерферируют, а одинаковых — складываются. При раскодировании будем просто смотреть на соответствующую компоненту: если там единичка, значит данное действительное число один раз было среди аргументов. Если двоечка — два раза, etc.

Для выражения через произведение (вместо суммы), просто проэкспоненциируем уже закодированные числа, перемножим их, и возьмём логарифм произведения.

Теперь попытаемся доказать второе предположение. А именно, что раскладывать симметричную функцию можно не только через суммы, а вообще через любые другие симметричные функции.

Короче говоря, нам нужно найти такую систему кодирования, которая бы «проводила всю нужную информацию» не только через оператор сложения, но через любую симметричную функцию. Каким условиям должна удовлетворять эта функция? Давайте рассмотрим несколько примеров.

Пусть наша функция — константа. Вполне симметрично. Разумеется, никакой информации об аргументах из результата не добудешь. Значит, одно условие уже есть. Множество значений должно совпадать по мощности с областью определения. (Будем называть такие множества множествами максимальной мощности.)

Возьмём функцию max, находящую максимум n своих аргументов. Из результата этой бяки можно выковырять информацию лишь об одном аргументе. Бяка. Нам так не пойдёт.

Попробуем сформулировать, чего нам нужно. Мы можем как угодно симметрично трансформировать аргументы. Т.е. можем позаботиться о том, чтобы каждый из аргументов лежал в неком подмножестве X области определения, совпадающем с ней по мощности. (Большего мы сделать, вроде бы, не можем) Позаботившись об этом, мы хотим, чтобы из функции можно было выковырять информацию о каждом аргументе, вне зависимости от других. Итак, нам нужно, чтобы:
Существовало такое множество X максимальной мощности, чтобы s была на множестве X^n инъективна в первом аргументе. Из инъективности в первом аргументе следует инъективность в каждом. Кроме того, раз s инъективна на множестве максимальной мощности, значит множество её значений тоже имеет максимальную мощность.
(Для суммы множество X — все натуральные/действительные числа. Для произведения — все натуральные/действительные числа больше нуля.)

Теперь нам нужно выделить среди множества X множество максимальной мощности Y, разные числа из которого в нашей функции не интерферируют.
(Для суммы это были числа вида (n+1)^x / базис Гимеля, для произведения — простые числа / экспоненты базиса Гимеля)

Ура! Мы выразили сумму через нашу почти произвольную симметричную функцию s.
Теперь мы можем выразить через неё любую симметричную функцию w, скомбинировав две выведенные формулы:
w(x, y, z) = W[x,y,z] = W°K°k[x,y,z] = W°K(k[x] + k[y] + k[z])
= W°K°g°s(f°k[x], f°k[y], f°k[z])

Как доказать аналогичную теорему для действительных чисел, думать пока лень. На последнее доказательство у меня ушло два часа времени, а мне вообще-то протокол писать надо. Тем более, что я пока не вижу в ней особенного смысла.

А вот куда более интересная штука. Если s — симметричная непрерывно-дифференцируемая функция на RR^n, то мы можем выразить её через сумму, причём функции перехода будут тоже непрерывно-дифференцируемы. Идея доказательства:
Функцию с непрерывной и всюду ненулевой производной всегда можно трансформировать в такую, у которой производная всегда будет единицой. (Натуральная параметризация.) Кажется, во многомерном случае, этого тоже можно добиться. Т.е. найти такие трансформационные функции, что D(f°s°g) = id. Функции перехода тоже получатся непрерывно-дифференцируемые.

Раз f°s°g непрерывно-дифференцируема, значит интеграл её дифференциала по некоторому пути будет равен разности на конечных значениях. Другими словами, значение f°s°g в точке p = (x, y, z) можно посчитать как сумму f°s°g(0) и интеграла Ds по некоторой кривой, соединяющей 0 и p. Самая лучшая кривая — путь по ребрам координатного паралеллипипеда p. Раз у нас D(f°s°g) = id, это будет просто сумма координат. Остаётся только показать, что существует k, такая что g(x,y,z) = k(x) + k(y) + k(z). Этого, кажется, несложно достичь по построению.

Источник

Презентация по математике «Симметрия в построении графиков функции»

XVI научная конференция молодых исследователей «Шаг в будущее»

Симметрия в построении графиков функции

Автор : Шматова Алёна Сергеевна, ученица 10 «А» класса, Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа №44

Научный руководитель: Шибко Елена Николаевна, учитель математики, Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа №44

Содержание

Аннотация

Данная исследовательская работа направлена на изучение использования симметрии в жизни человека и математических науках; изучение теоретической стороны темы; проведение практической работы по теме «Симметрия». Изучив проблему симметрии, мы увидели, что симметрия присутствует и в прошлом, и в настоящем, и в будущем. Симметрия – это не только математическое понятие. Его заимствовали из природы. А так как человек – это часть природы, то человеческое творчество во всех его проявлениях тяготеет к симметрии. Симметрия в живой природе: в животном и растительном мире, передаётся генетически из поколения в поколение.

Введение

Симметрия… является той идеей, посредством

которой человек на протяжении веков пытался

постичь и создать порядок, красоту и

Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека, и употреблялось скульпторами ещё в V веке до н. э.

Слово «симметрия» греческое. Оно означает «соразмерность», «пропорциональность», одинаковость в расположении частей. Его широко используют все без исключения направления современной науки.

Об этой закономерности задумывались многие великие люди. Например, Л.Н. Толстой говорил: «Стоя перед чёрной доской и рисуя на ней мелом разные фигуры, я вдруг был поражён мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врождённое чувство. На чём же оно основано?»

Симме́три́я (др.-греч. συμμετρία — «соразмерность»), в широком смысле — неизменность при каких-либо преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.

С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Отметим, например, симметрию, свойственную бабочке и кленовому листу, симметрию автомобиля и самолета, симметрию в ритмическом построении стихотворения и музыкальной фразы, симметрию орнаментов и бордюров, симметрию атомной структуры молекул и кристаллов. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.

узнать где и как используется симметрия в жизни человека.

Выяснить, кто первым обратил внимание на использование симметрии в жизни человека.

Выявить где используется центральная симметрия.

Выявить где используется осевая симметрия.

Выяснить, как легче строить графики симметричных функций.

Выявить, можно ли наблюдать симметрию в неживой природе.

Проанализировать симметрию в природе и связь природы с математикой.

Определить связь между симметрией в природе, математики, физике, архитектуры.

Выявить симметричные функции.

Доказать, что существуют такие функции, которые связанны с природой.

Гипотеза: Симметрия существует в природе, математики, физике, архитектуре.

Объект исследования: симметрия в природе, математики, физике, архитектуре.

Методы исследования: изучение, анализ и обобщение данных научной литературы, наблюдение, фотографирование, анкетирование, интервьюирование, эксперимент, количественный и качественный учет данных, обработка и анализ полученных данных.

Глава 1. Симметрия

Симметрия является той идеей, посредством которой человек на протяжении веков пытался

постичь и создать порядок, красоту и

Формы восприятия и выражения во многих областях науки и искусства, в конечном счёте, опираются на симметрию, используемую и проявляющуюся в специфических понятиях и средствах, присущих отдельным областям науки и видам искусства.

Действительно, симметричные объекты окружают нас буквально со всех сторон, мы имеем дело с симметрией везде, где наблюдается какая-либо упорядоченность. Симметрия противостоит хаосу, беспорядку. Получается, что симметрия – это уравновешенность, упорядоченность, красота, совершенство.

Весь мир можно рассмотреть как проявление единства симметрии и асимметрии. Асимметричное в целом сооружение может являть собой гармоничную композицию из симметричных элементов.

Симметрия многообразна, вездесуща. Она создает красоту и гармонию.

Идея симметрии часто является отправным пунктом в гипотезах и теориях учёных прошлых веков, веривших в математическую гармонию мироздания и видевших в этой гармонии проявление божественного начала. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна. В своих размышлениях над картиной мироздания человек с давних времен активно использовал идею симметрии.

Глава 2. Виды симметрии

«симметрией» в математике понимается такое преобразование пространства (плоскости), при котором каждая точка M переходит в другую точку M’ относительно некоторой плоскости (или прямой), когда отрезок MM’ является перпендикулярным плоскости (или прямой) и делится ею пополам. Плоскость (прямая) называется при этом плоскостью (или осью) симметрии.

Осью симметрии L называется такая прямая линия, вокруг которой симметричная фигура может быть повернута несколько раз таким образом, что каждый раз фигура «самосовмещается» сама с собой в пространстве. Число таких поворотов вокруг оси

Наконец, центром симметрии C называется такая особая точка внутри фигуры, характеризующаяся тем, что любая проведенная через точку прямая по обе стороны от нее и на равных расстояниях встречает одинаковые (соответственные) точки фигуры. «Идеальным» примером такой фигуры является шар, центр которого и является его центром симметрии.

Симметрия широко встречается в объектах живой и неживой природы. Например, симметрия в химии отражается в геометрической конфигурации молекул. Так, например, молекула метана СH4 обладает симметрией тетраэдра. Понятие «симметрии» является центральным при исследовании кристаллов. При этом симметрия внешних форм кристаллов определяется симметрией его атомного строения, которая обуславливает и симметрию физических свойств кристалла.

Особенно широко понятие «симметрии» применительно к физическим законам используется в современной физике. Если законы, устанавливающие соотношения между величинами или определяющие изменение этих величин со временем, не меняются при определенных операциях (преобразованиях), которым может быть подвергнута система, то говорят, что эти законы обладают симметрией (или инвариантны) относительно данных преобразований. Например, закон тяготения действует в любой точки пространства, то

есть он является инвариантным по отношению переноса системы как целого в пространстве.

На явление симметрии в живой природе обратили внимание еще пифагорейцы в связи с развитием ими учения о гармонии. Установлено, что в природе наиболее распространенной «Зеркальной» симметрией обладает бабочка, листок или жук (Рис.2) и часто такой вид симметрии называется «симметрией листка» или «билатеральной симметрией». К формам с лучевой симметрией относятся гриб, ромашка, сосновое дерево и часто такой вид симметрии называется «ромашко-грибной» симметрией.

Рис.2

Еще в 19-м веке исследования в этой области привели к заключению, что симметрия природных форм в значительной степени зависит от влияния сил земного тяготения, которое в каждой точке имеет симметрию конуса. В результате был найден следующий закон, которому подчиняются формы природных тел:

Все то, что растет или движется по вертикали, то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой («ромашко-грибной») симметрии (рис.3б). Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии – «симметрии листка» (одна плоскость симметрии) рис.3а.

рис.3б радиально-лучевая симметрия

Принцип симметрии очень часто используется совместно с принципом «золотого сечения». Таким примером может служить картина Рафаэля «Обручение Марии».

Глава 3. Симметрия в построении графиков функции.

Две точки А и А называются симметричными относительно точки О, если О – середина отрезка АА . Точка О считается симметричной самой себе.

Точка М называется симметричной точке М относительно прямой а, если прямая ММ перпендикулярна прямой а и МО = ОМ , где О — точка пересечения прямых ММ и а.

Преобразование фигуры F в фигуру F , при котором каждая ее точка переходит в точку, симметричную относительно данной прямой, называется преобразованием симметрии относительно прямой а. Прямая а называется осью симметрии.

Если при переносе плоской фигуры F вдоль заданной прямой АВ на расстояние а (или кратное этой величине) фигура совмещается сама с собой, то говорят о переносной симметрии. Прямая АВ называется осью переноса, расстояние а элементарным переносом или периодом.

Свойство 1. График четной функции симметричен относительно оси ОУ.

Доказательство. Пусть y= f(x) — четная функция, тогда f(-x) = f(x). Рассмотрим произвольную точку графика M(x ; f(х )) и точку М (- x ; f (- x )). Так как функция

у = f(х) — четная, то f( х ) = f (-х ) =>вторые координаты точек М и M равны. Точки графика М и M симметричны относительно оси ОУ. Так как М — произвольная точка графика, то, значит, график четной функции симметричен относительно оси ОУ.

Свойство 2. График нечетной функции симметричен относительно начала координат.

Точки графика М и M симметричны относительно начала координат. Так как М —произвольная точка графика, то, значит, график четной функции симметричен относительно начала координат.

а) у=х

Докажем, что ось ОУ является осью симметрии данного графика.

у(-а) = (-а) = а , y(a) = a => y(a) = y(-a) => y = x — четная функция (определение 1) => ось ОУ является осью симметрии данного графика.

Докажем, что никакая другая прямая не будет являться осью симметрии.

Предположим, что некоторая прямая х = х является осью симметрии, тогда

у (x + a) = (x +а) = х + 2х а + а => y(x + a) у(x –a) => у(x –a) = (x +а) =

= х — 2х а + а

прямая х = х не является осью симметрии данного графика.

б) y= ax + bx + c.

Докажем, что для данного графика ось симметрии будет проходить через вершину параболы (x ; y ) параллельно оси ОУ.

Первую координату вершины параболы можно вычислить по формуле:

. Рассмотрим произвольную точку графика M(x +а; у (х +а)) и точку

М (x — а; у ( x — а)).

у(x +а) = а(x +а) + b(x +а)+с = а x + 2а x + а + bx + аb + с =

Значит, точки М и М симметричны относительно прямой, проходящей через вершину параболы y= ax + bx + c. Следовательно, график данной функции симметричен относительно прямой

в) у= х .

Докажем, что начало координат будет точкой симметрии данного графика.

симметрии данного графика является начало координат (доказательство 2).

Графиком данной функции является прямая.

1. Каждая точка, принадлежащая этой прямой, будет являться ее центром симметрии, т.е. у этого графика бесконечно много центров симметрии.

Рассмотрим точку М(x ;y ). Пусть M ( x ; y )—точка графика данной функции, отличная от точки М, а точка М такая точка графика, что М M =М М . Тогда первая координата

точки М равна 2 x — x . Убедимся, что точка М принадлежит графику данной функции.

у = k(2 x — x )+ b

y= 2kx — k х +b

Следовательно, точка М принадлежит графику функции.

Осью симметрии данного графика будет являться прямая параллельная оси ОУ и проходящая через некоторую координату (x ; 0), которая принадлежит графику функции.

у(-х) = k|-x|+b = k|x| + b = у(х) => функция y = k|x| + b является четной (определение 1) Значит, она симметрична относительно оси ОУ.

з)y = а + b│х│+с.

у(-х) = а(-х) + b│-х│+с = ах + b│х│+с = у(х). => ось ОУ является осью симметрии данного графика.

и) y=│ax +bx+c│

Так же мы знаем, что через вершину параболы ( х ; у ) проходит прямая, параллельная оси ординат, которая является осью симметрии параболы.(2)

Из свойств (1) и (2), следует, что ось симметрии параболы является осью данного графика.

Заключение

С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.

Существует множество видов симметрии, как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.

Симметрия в алгебре и геометрии имеет большое значение. Я рассмотрела основные теории, связанные с симметрическими системами уравнений. Научилась решать симметрические системы уравнений, и узнала кое-что новое про симметрию графиков функций. Выбранная тема актуальна, так как в средней школе не рассматриваются все виды симметрий в алгебре и геометрии.

Источник