что такое сечение инженерная графика

Сечения в инженерной графике на чертежах с примерами

Содержание:

Сечение — изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями. На сечении показывается только то, что получается непосредственно в секущей плоскости.

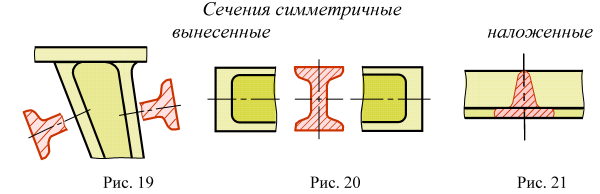
Сечения, не входящие в состав разреза, разделяют на вынесенные (рис. 19, 20) и наложенные (рис. 21).

Лучше использовать вынесенные сечения. Их допускается располагать в разрыве между частями одного и того же вида (рис. 20).

Ось симметрии вынесенного (по следу секущей плоскости или в разрыве) или наложенного сечения (рис. 19, 21) выполняют штрихпунктирной тонкой линией без обозначения буквами и стрелками и линию сечения не проводят.

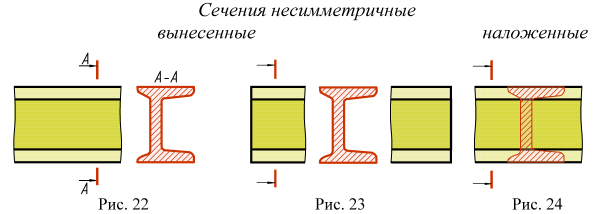
Для несимметричных сечений, расположенных в разрыве (рис. 23) или наложенных (рис. 24), линию сечения проводят со стрелками, но буквами не обозначают.

Условности при выполнении сечений

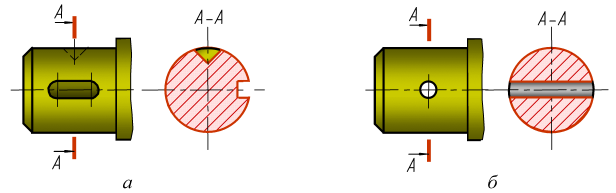
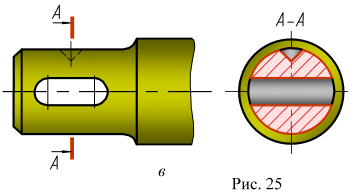
Если секущая плоскость проходит через ось поверхности вращения, ограничивающей отверстие или углубление, то контур отверстия или углубления в сечении показывают полностью (рис. 25, а, б), то есть сечение выполняют по типу разреза.

В случае некруглого отверстия и если при выполнении сечения изображение распадается на отдельные самостоятельные части, то вместо сечения нужно применять разрезы (рис. 25, в).

Сечения и правила оформления на чертежах (ГОСТ 2306-68)

Сечением называется изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями.

В отличие от разреза на сечении показывается только то, что расположено непосредственно в секущей плоскости, все, что лежит за ней, не изображается.

Сечения в зависимости от расположения их на чертеже делятся на вынесенные и наложенные. Вынесенные сечения располагают на свободном месте поля чертежа или в разрыве изображения предмета. Наложенные сечения располагают на соответствующем изображении предмета.

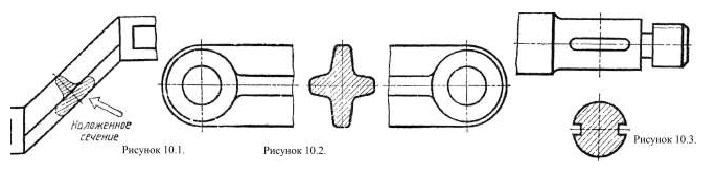
Симметричные наложенные сечения (рисунок 10.1) и в разрыве (рисунок 10.2) буквами и стрелками не обозначаются и линию сечения не показывают.

Если ось симметрии симметричного вынесенного сечения совпадает со следом секущей плоскости, то такое сечение также не обозначается и не подписывается (рисунок 10.3).

Предпочтительны вынесенные сечения. Их контур вычерчивают сплошными толстыми линиями. Контуры наложенных сечений вычерчивают сплошными тонкими линиями.

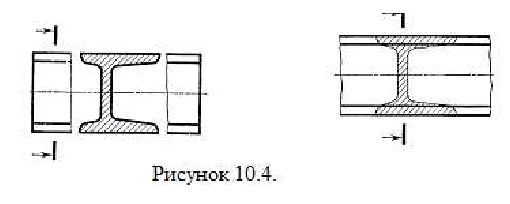
Для несимметричных сечений, расположенных в разрыве или наложенных, положение секущей плоскости указывается линией сечения со стрелками, но буквами не обозначается (рисунок 10.4).

Во всех остальных случаях выполнения сечений положение секущей плоскости должно быть показано линией сечения с указанием стрелками направления взгляда, а над самими сечениями выполняется надпись.

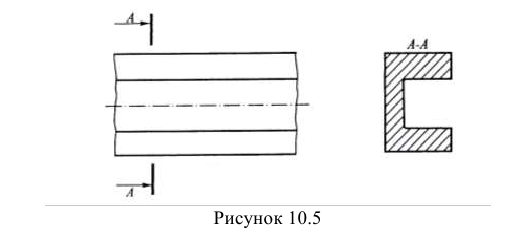
При совпадении секущей плоскости с осью поверхности вращения, ограничивающей отверстие или углубление, контур отверстия или углубления в сечении показывается полностью, хотя этот контур и не расположен в секущей плоскости, т.е. сечение оформляется как разрез (смотри рисунок 10.5).

Если секущая плоскость проходит через некруглые отверстия и сечение получается состоящим из отдельных частей, то сечение должно быть заменено разрезом.

Сечения и правила обозначения на чертежах

Правила изображения и обозначения сечений устанавливает стандарт [11].

Сечение – изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями. На сечении показывается только то, что получается непосредственно в секущей плоскости. В зависимости от определенных условий сечения подразделяют, как показано на рис. 96.

Вынесенное сечение

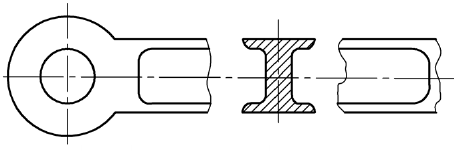
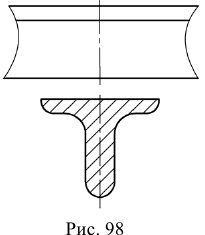
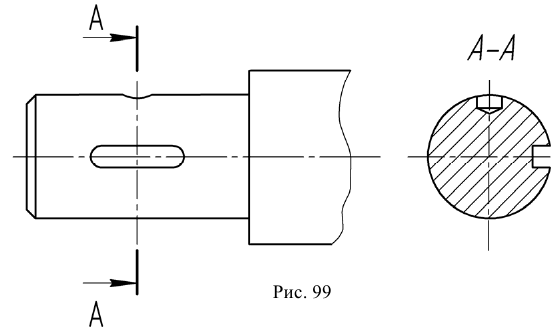
Предпочтительными являются вынесенные сечения. Вынесенные сечения располагаются вне изображения детали: 1) в разрыве между частями одного и того же изображения (рис. 97); 2) на продолжении следа секущей плоскости (рис. 98); на свободном месте поля чертежа (рис. 99)

В разрыве между частями изображения и на продолжении следа секущей плоскости рекомендуется располагать симметричные сечения, тогда они не обозначаются (рис. 97). Если сечение располагается на свободном поле чертежа, то оно обозначается так же, как обозначаются разрезы (рис. 99)

Для сечений всех видов, когда секущая плоскость проходит через ось вращения цилиндрического, конического, сферического углублений или сквозного отверстия, контуры углублений и отверстий должны быть вычерчены полностью (рис. 99).

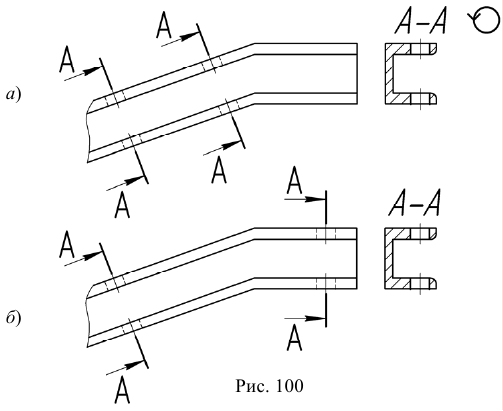
Контур вынесенного сечения всегда обводится сплошной толстой линией. Для ряда одинаковых сечений, относящихся к одной и той же детали, линии сечения следует обозначать одной и той же буквой и вычерчивать одно сечение (рис. 100а). Если секущие плоскости направлены под разными углами, то условное обозначение не наносится (рис. 100б).

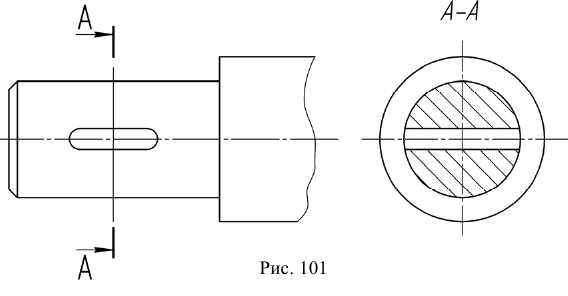
Если секущая плоскость проходит через некруглое отверстие и сечение получается состоящим из отдельных самостоятельных частей, то вместо сечения следует применять разрез (рис. 101).

Наложенное сечение

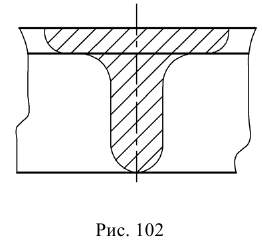
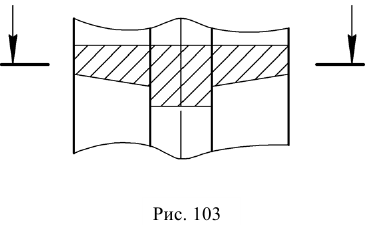
Наложенные сечения вычерчиваются непосредственно на изображении детали. Контур его обводится сплошной тонкой линией (S/2 – S/3). В месте расположения наложенного сечения линии контура изображения детали не прерываются (рис. 102, 103).

Наложенное сечение не обозначается, если оно симметрично (рис. 102). Для несимметричных наложенных сечений указывают положение секущей плоскости и направление взгляда (рис. 103). Наложенные сечения рекомендуется применять в тех случаях, когда контур его не пересекается никакими линиями видимого контура детали.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Рассмотрим некоторые основные положения этого стандарта и рекомендации справочной и учебной литературы.

Изображения

Изображение в общем случае можно рассматривать как проекцию пространственного объекта на плоскость. Правила построения изображений применяемые в инженерной графике приведены в разделе «Система координат и плоскости проекций, применяемые в инженерной графике».

Изображения на чертеже в зависимости от их содержания разделяются на виды, разрезы, сечения.

Количество изображений (видов, разрезов, сечений) должно быть наименьшим, но обеспечивающим полное представление о предмете при применении установленных в соответствующих стандартах условных обозначений, знаков и надписей.

Вид— изображение обращенной к наблюдателю видимой части поверхности предмета. Для уменьшения количества изображений допускается на видах показывать необходимые невидимые части поверхности предмета при помощи штриховых линий.

Устанавливаются следующие названия видов, получаемых на основных плоскостях проекций:

1- вид спереди (главный вид);

Названия видов на чертежах надписывать не следует, за исключением случая, когда виды сверху, слева, справа, снизу, сзади не находятся в непосредственной проекционной связи с главным изображением (видом или разрезом, изображенным на фронтальной плоскости проекций).

При нарушении проекционной связи, направление проектирования должно быть указано стрелкой около соответствующего изображения. Над стрелкой и над полученным изображением (видом) следует нанести одну и ту же прописную букву (рис. 1 вид Д). Чертежи оформляют так же, если перечисленные виды отделены от главного изображения другими изображениями или расположены не на одном листе с ним.

Рисунок 1. Корпусная деталь

Если какую-либо часть предмета невозможно показать на основных видах без искажения формы и размеров, то применяют дополнительные виды, получаемые на плоскостях, непараллельных основным плоскостям проекций (рис. 2, 3, 4).

Рисунок 2. Расположение и обозначение дополнительного вида

Рисунок 3. Расположение и обозначение дополнительного вида

Дополнительный вид должен быть отмечен на чертеже прописной буквой (рис. 2, 3), а у связанного с дополнительным видом изображения предмета должна быть поставлена стрелка, указывающая направление взгляда, с соответствующим буквенным обозначением (стрелка Б, рис. 2, 3).

Когда дополнительный вид расположен в непосредственной проекционной связи с соответствующим изображением, стрелку и обозначение вида не наносят (рис. 4).

Дополнительный вид допускается повертывать, но с сохранением, как правило, положения, принятого для данного предмета на главном изображении; при этом обозначение вида должно быть дополнено условным графическим обозначением .

Рисунок 4 Дополнительный вид построенный без нарушения проекционной связи

Несколько одинаковых дополнительных видов, относящихся к одному предмету, обозначают одной буквой и вычерчивают один вид. Если при этом связанные с дополнительным видом части предмета расположены под различными углами, то к обозначению вида условное графическое обозначение не добавляют.

Рисунок 5. Размеры стрелок определяющих направление взгляда

Разрезы

Разрезы разделяются, в зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций, на:

В строительных чертежах горизонтальным разрезам могут присваиваться другие названия, например, «план»;

В зависимости от числа секущих плоскостей разрезы разделяются на:

Рисунок 6. Виды разрезов

Рисунок 7. Продольный разрез пружины

Рисунок 8. Поперечный разрез детали

Начальный и конечный штрихи не должны пересекать контур соответствующего изображения.

У начала и конца линии сечения, а при необходимости и у мест пересечения секущих плоскостей ставят одну и ту же прописную букву русского алфавита. Буквы наносят около стрелок, указывающих направление взгляда, и в местах пересечения со стороны внешнего угла.

Разрез должен быть отмечен надписью по типу «А-А» (всегда двумя буквами через тире).

В строительных чертежах у линии сечения взамен букв допускается применять цифры, а также надписывать название разреза (плана) с присвоенным ему буквенным, цифровым или другим обозначением.

Когда секущая плоскость совпадает с плоскостью симметрии предмета в целом, а соответствующие изображения расположены на одном и том же листе в непосредственной проекционной связи и не разделены какими – либо другими изображениями, для горизонтальных, фронтальных и профильных разрезов не отмечают положение секущей плоскости, и разрез надписью не сопровождают.

Фронтальным и профильным разрезам, как правило, придают положение, соответствующее принятому для данного предмета на главном изображении чертежа. Горизонтальные, фронтальные и профильные разрезы могут быть расположены на месте соответствующих основных видов.

Рисунок 9. Построение ломанного разреза

Рисунок 10. Изображение элементов детали, расположенных за секущей плоскостью, при построении ломанного разреза

Рисунок 11. Местный разрез, ограниченный сплошной волнистой линией

Рисунок 12. Местный разрез, ограниченный сплошной тонкой линией с изломом

Рисунок 13. Совмещение на изображении части вида и разреза

Рисунок 14. Совмещение на изображении части вида и разреза

Рисунок 15. Совмещение на изображении части вида и разреза

Рисунок 16. Совмещение на изображении части вида и разреза

Если в симметричной детали ось симметрии совпадает с линией контура, границу вида и разреза смещают от оси и оформляют как показано на рисунке 14.

Допускается соединять четверть вида и четверти трех разрезов: четверть вида, четверть одного разреза и половину другого и т. п. при условии, что каждое из этих изображений в отдельности симметрично.

Рисунок 17. Совмещение на изображении части вида и разреза

Сечения

Рисунок 18. Оформление вынесенного сечения

Рисунок 19. Использование цилиндрической поверхности в качестве секущей

Контур вынесенного сечения, а также сечения, входящего в состав разреза, изображают сплошными основными линиями, а контур наложенного сечения – сплошными тонкими линиями, причем контур изображения в месте расположения наложенного сечения не прерывают.

Рисунок 20. Оформление вынесенного сечения

Рисунок 21. Оформление наложенного сечения

Рисунок 22. Образец оформления вынесенного сечения

Рисунок 23. Обозначение несимметричного вынесенного сечения

Рисунок 24. Обозначение несимметричного наложенного сечения

Рисунок 25. Оформление нескольких одинаковых сечений

Рисунок 26. Оформление нескольких одинаковых сечений

Когда расположение одинаковых сечений точно определено изображением или размерами, допускается наносить одну линию сечения, а над изображением сечения указывать количество сечений.

Рисунок 27. Оформление сечения, проходящего через ось поверхности вращения

Выносные элемент ы

Выносной элемент – дополнительное отдельное изображение (обычно увеличенное) какой – либо части предмета, требующей графического и других пояснений в отношении формы, размеров и иных данных.

Выносной элемент следует располагать, по возможности, ближе к соответствующему месту на изображении предмета.

Рисунок 28. Оформление выносного элемента

Условности и упрощения

Условности и упрощения это правила позволяющие сделать чертеж более простым, понятным и уменьшить время на его выполнение. ГОСТ 2.305-68 устанавливает следующие условности и упрощения:

Рисунок 30. Образец изображения равномерно расположенных элементов

Рисунок 31. Образец изображения равномерно расположенных элементов

Рисунок 32. Образец оформления линий пересечения поверхностей

Рисунок 33. Образец оформления линий пересечения поверхностей

Рисунок 34. Образец оформления плавного перехода от одной поверхности к другой

Рисунок 35. Образец оформления плавного перехода от одной поверхности к другой

Рисунок 36. Образец оформления плавного перехода от одной поверхности к другой

Рисунок 37. Образец оформления плавного перехода от одной поверхности к другой

Рисунок 38. Образец оформления плавного перехода от одной поверхности к другой

Рисунок 39. Образец оформления плавного перехода от одной поверхности к другой

Рисунок 40. Образец оформления плавного перехода от одной поверхности к другой

Рисунок 41. Образец оформления плавного перехода от одной поверхности к другой

6. Пластины, а также элементы деталей (отверстия, фаски, пазы, углубления и т. п.) размером (или разницей в размерах) на чертеже 2 мм и менее изображают с отступлением от масштаба, принятого для всего изображения, в сторону увеличения.

Рисунок 42. Образец изображения незначительных уклонов

Рисунок 43. Образец изображения незначительной конусности

9. Предметы или элементы, имеющие постоянные или закономерно изменяющееся поперечное сечение (валы, цепи, прутки, фасонный прокат, шатуны и т. п.), допускается изображать с разрывами. Частичные изображения и изображения с разрывами ограничивают одним из следующих способов:

Рисунок 44. Образец обозначения плоских поверхностей

Рисунок 45. Образцы изображения предметов, имеющих постоянное или закономерно изменяющиеся сечение

11. Для упрощения чертежей или сокращения количества изображений допускается:

Рисунок 46. Образцы изображения предметов, имеющих постоянное или закономерно изменяющиеся сечение

Рисунок 47. Образцы изображения предметов, имеющих постоянное или закономерно изменяющиеся сечение

Рисунок 48. Образец изображения накатки

Рисунок 49. Изображение части предмета, находящейся между наблюдателем и секущей плоскостью

Рисунок 50. Образец применения сложного разреза

Рисунок 51. Образец изображения отверстия в ступице зубчатого колеса

Рисунок 52. Пример совмещения разрезов

13. Условности и упрощения, допускаемые в неразъемных соединениях, в чертежах электротехнических и радиотехнических устройств, зубчатых зацеплений и т. д., устанавливаются соответствующими стандартами.

Источник

Что такое сечение инженерная графика

Автор видеоурока: к.пед.н., доцент кафедры ИГиСАПР Кайгородцева Н.В.

СЕЧЕНИЯ

На рис. 274, а показан чертеж рычага. Главный вид и вид сверху с двумя местными разрезами не выявляют форму его средней части. Форму средней части можно показать с помощью профильного разреза (рис. 274, б), но элементы, расположенные за секущей плоскостью, не дают дополнительную информацию о форме детали и являются лишними. В таких случаях удобно применять изображение, называемое сечением (рис. 274, в).

Сечением называется изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями, на сечении показывается только то, что расположено непосредственно в секущей плоскости.

В случае, показанном на рис. 274, вместо профильного разреза достаточно выполнить сечение (рис. 274, в). Применение сечений сокращает графическую работу при выполнении чертежа.

В отличие от разреза на сечении показывается только то, что расположено непосредственно в секущей плоскости, все, что лежит за ней, не изображается. На рис. 275 наглядно показано различие между сечением и разрезом.

Сечения в зависимости от расположения их на чертеже делятся на вынесенные и наложенные. Вынесенные сечения располагают на свободном месте поля чертежа (рис. 276, а) или в разрыве изображения предмета (рис. 276, в). Наложенные сечения располагают на соответствующем изображении предмета (рис. 276, б).

Предпочтительны вынесенные сечения. Их контур вычерчивают сплошными толстыми линиями (рис. 276, а). Контуры наложенных сечений вычерчивают сплошными тонкими линиями.

В случаях, подобных показанным на рис. 276, при симметричной фигуре сечения положение секущей плоскости не указывается.

Для несимметричных сечений, расположенных в разрыве или наложенных, положение секущей плоскости указывается линией сечения со стрелками, но буквами не обозначается (рис. 277, а и б).

Во всех остальных случаях выполнения сечений положение секущей плоскости должно быть показано линией сечения с указанием стрелками направления взгляда, а над самими сечениями выполняется надпись (рис. 278, а и б).

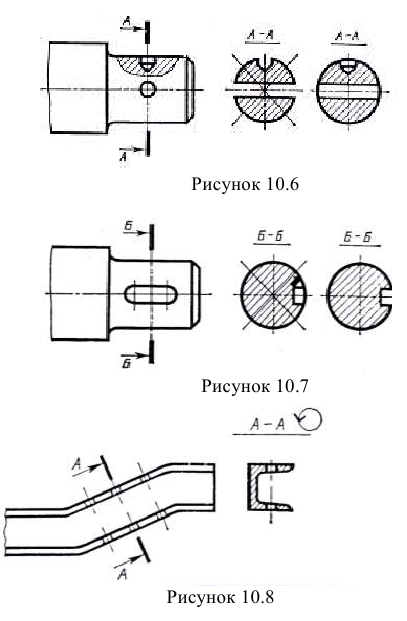
При совпадении секущей плоскости с осью поверхности вращения, ограничивающей отверстие или углубление, контур отверстия или углубления в сечении показывается полностью, хотя этот контур и не расположен в секущей плоскости (рис. 277, в, см. стрелки К), т. е. сечение оформляется как разрез. Если секущая плоскость проходит через некруглые отверстия (рис. 279, а) и сечение получается состоящим из отдельных частей (рис. 279, б), то сечение должно быть заменено разрезом (рис. 279, в).

Сечение может выполняться несколькими секущими плоскостями, как на рис. 279, г.

Допускается вместо секущих плоскостей применять секущие цилиндрические поверхности, развертываемые затем в плоскость. На рис. 280 деталь имеет различные отверстия. Форму этих отверстий удобно выявить, применяя развернутое сечение детали секущей цилиндрической поверхностью, указанной линией сечения со стрелками и буквами. Над развернутым сечением выполняется надпись теми же буквами с добавлением слова «развернуто».

ВЫНОСНЫЕ ЭЛЕМЕНТЫ

В тех случаях, когда на основном изображении невозможно изобразить мелкие элементы изделия со всеми подробностями, применяют выносные элементы.

Выносным элементом называют дополнительное отдельное изображение в увеличенном виде какой-либо части изделия, требующей графического и других пояснений в отношении формы, размеров и иных данных.

При применении выносного элемента соответствующее место изображения отмечают замкнутой сплошной тонкой линией (окружностью или овалом) с обозначением римской цифрой порядкового номера выносного элемента на полке линии-выноски (рис. 281).

Над выносным элементом указывается та же цифра и масштаб, в котором выполнен выносной элемент (масштабы могут быть различные).

Выносной элемент следует располагать возможно ближе к соответствующему месту на изображении предмета. Выносной элемент может содержать подробности, не указанные на соответствующем изображении, и может отличаться от него по содержанию. Например, изображение может быть видом, а выносной элемент — разрезом.

Источник

• ← что делать с фурункулами
• что такое реконструктивные операции на костях голени бедра таза →