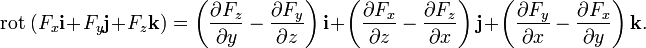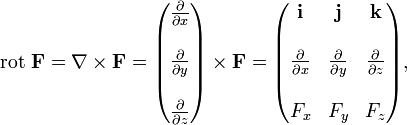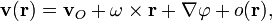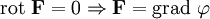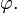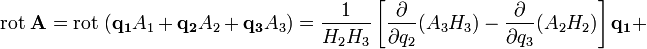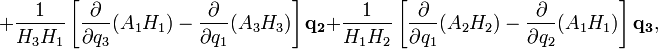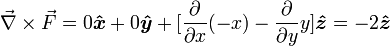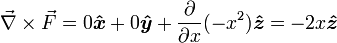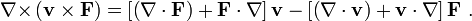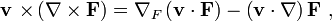что такое ротор вектора
Ротор векторного поля
Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной литературе), а также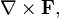 
где 
— векторный дифференциальный оператор набла.
Содержание
Математическое определение
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
.
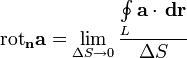
Нормаль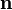 
к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.
В трёхмерной декартовой системе координат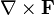 
вычисляется следующим образом:
Для удобства запоминания можно условно представлять ротор как векторное произведение:
где i, j и k — единичные орты для осей x, y и z соответственно.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).
Физическая интерпретация
По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением
где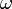 
— вектор углового вращения элемента среды в точке О, а 
— квадратичная форма от координат — потенциал деформации элемента среды.
Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор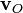 
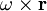
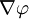
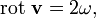
), вращательного движения (вектор 
) и потенциального движения — деформации (вектор 
). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство 
и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
Например, если в качестве векторного поля взять поле скоростей ветра на Земле, то в северном полушарии для антициклона, вращающегося по часовой стрелке, ротор будет направлен вниз, а для циклона, вращающегося против часовой стрелки — вверх. В тех местах, где ветры дуют прямолинейно и с одинаковой скоростью, ротор будет равен нулю (у неоднородного прямолинейного течения ротор ненулевой).
Основные свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
для любых векторных полей F и G и для всех вещественных чисел a и b.
При этом верно и обратное: если поле F бездивергентно, оно есть поле вихря некоторого поля G:
Верно и обратное: если поле безвихревое, то оно потенциально:
для некоторого скалярного поля 
Ротор
Ротор (Вихрь) — векторный оператор векторного поля, показывает насколько и в какую сторону закручено поле в каждой точке. Ротор обозначается значком rot или :
, где
векторный дифференциальный оператор набла, и F изучаемое векторное поле. В декартовой системе координат
вычисляется следующим образом:
Для простоты восприятия можно представлять ротор как
Или как детерминант следующей матрицы:
где i, j и k — единичные векторы для осей x, y и z соответственно.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).
Физическая интерпретация
Основные свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
для любых векторных полей F и G и для всех действительных чисел a и b.
Ротор
Ротор (Вихрь) — векторный оператор векторного поля, показывает насколько и в какую сторону закручено поле в каждой точке. Ротор обозначается значком rot или :
, где
векторный дифференциальный оператор набла, и F изучаемое векторное поле. В декартовой системе координат
вычисляется следующим образом:
Для простоты восприятия можно представлять ротор как
Или как детерминант следующей матрицы:
где i, j и k — единичные векторы для осей x, y и z соответственно.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).
Физическая интерпретация
Основные свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
для любых векторных полей F и G и для всех действительных чисел a и b.
Ротор (вектор)
Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной литературе), а также 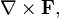где — векторный дифференциальный оператор набла.
Содержание
Математическое определение
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
.
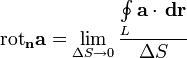
Нормаль 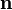к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.
В трёхмерной декартовой системе координат 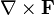вычисляется следующим образом:
Для удобства запоминания можно условно представлять ротор как векторное произведение:
где i, j и k — единичные орты для осей x, y и z соответственно.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).
Физическая интерпретация
По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением
где 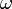— вектор углового вращения элемента среды в точке О, а — квадратичная форма от координат — потенциал деформации элемента среды.
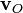
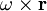
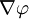
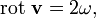
Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор ), вращательного движения (вектор ) и потенциального движения — деформации (вектор ). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
Например, если в качестве векторного поля взять поле скоростей ветра на Земле, то в северном полушарии для антициклона, вращающегося по часовой стрелке, ротор будет направлен вниз, а для циклона, вращающегося против часовой стрелки — вверх. В тех местах, где ветры дуют прямолинейно и с одинаковой скоростью, ротор будет равен нулю (у неоднородного прямолинейного течения ротор ненулевой).
Основные свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
для любых векторных полей F и G и для всех вещественных чисел a и b.
При этом верно и обратное: если поле F бездивергентно, оно есть поле вихря некоторого поля G:
Верно и обратное: если поле безвихревое, то оно потенциально:
для некоторого скалярного поля
Ротор в ортогональных криволинейных координатах
Примеры
Простое векторное поле
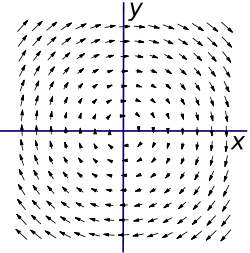
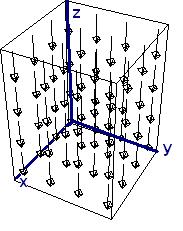
Рассмотрим векторное поле, линейно зависящее от координат x и y:
.
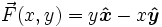
Очевидно, что поле закручено. Если мы поместим колесо с лопастями в любой области поля, мы увидим, что оно начнет вращаться по направлению часовой стрелки. Используя правило правой руки, можно ожидать ввинчивание поля в страницу. Для правой системы координат направление в страницу будет означать отрицательное направление по оси z.
Как и предположили, направление совпало с отрицательным направлением оси z. В данном случае ротор является константой, так как он независим от координаты. Количество вращения в приведенном выше векторном поле одно и то же в любой точке (x,y). График ротора F не слишком интересен:
Более сложный пример
Теперь рассмотрим несколько более сложное векторное поле:
.
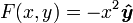
Три общих примера
Рассмотрим пример ∇ × [ v × F ]. Используя прямоугольную систему координат, можно показать, что
Если v и ∇ поменять местами:
что является фейнмановской записью с нижним индексом ∇F, что значит, что градиент с индексом F относится только к F.
Другой пример ∇ × [ ∇ × F ]. Используя прямоугольную систему координат, можно показать, что:
что можно считать частным случаем первого примера с подстановкой v → ∇.
Поясняющие примеры
Примечания
См. также
Полезное
Смотреть что такое «Ротор (вектор)» в других словарях:
РОТОР — (от лат. roto вращаю) (вихрь) одна из осн. операций векторногоанализа, сопоставляющая векторному полю а(r )др. векторное полеrot а (используются также обозначения curl а). Если точка r задана своими декартовыми координатами, а вектор а своими… … Физическая энциклопедия
Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение … Википедия
Ротор (матем.) — Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной… … Википедия
Ротор векторного поля — Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной… … Википедия
Ротор поля — Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной… … Википедия
ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… … Энциклопедия Кольера
Ротор — Роторный экскаватор как экспонат в бывшем угольном карьере «стальном городе» Феррополис (Германия), превращенном в музей под открытым небом Ротор от лат. roto ) вращаться В математике: Ротор то же, что вихрь векторного поля, то… … Википедия
Ротор Дарье — У этого термина существуют и другие значения, см. Ротор. Ротор Дарье, турбина Дарье (Darrieus rotor) тип турбины низкого давления, ось вращения которой перпендикулярна потоку жидкой или газовой среды. Предложена в 1931 году французским… … Википедия
ротор — (лат. rotare вращать) 1) вращающаяся часть электрической машины (генератора или двигателя) внутри неподвижной части статора; 2) вращающаяся часть паровой турбины, компрессора, гидронасоса, гидромотора и т. д.; 3) несущий винт вертолета; 4) мат.… … Словарь иностранных слов русского языка
ротор — а, ч. 1) спец.Обертова частина машин, за допомогою якої енергія одного виду перетворюється в енергію іншого виду. 2) Гвинт вертольота. 3) мат. Вектор, який характеризує обертовий рух у даній точці векторного поля … Український тлумачний словник
Ротор (математика)
Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной литературе), а также где — векторный дифференциальный оператор набла.
Содержание
Математическое определение
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
.
Нормаль к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.
В трёхмерной декартовой системе координат вычисляется следующим образом:
Для удобства запоминания можно условно представлять ротор как векторное произведение:
или как определитель следующей матрицы:
где i, j и k — единичные орты для осей x, y и z соответственно.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).
Физическая интерпретация
По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением
где — вектор углового вращения элемента среды в точке О, а — квадратичная форма от координат — потенциал деформации элемента среды.
Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор ), вращательного движения (вектор ) и потенциального движения — деформации (вектор ). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
Основные свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
для любых векторных полей F и G и для всех действительных чисел a и b.
При этом верно и обратное: если поле F бездивергентно, оно есть поле вихря некоторого поля G:
Верно и обратное: если поле безвихревое, то оно потенциально:
для некоторого скалярного поля
Ротор в ортогональных криволинейных координатах
Примеры
Простое векторное поле
Рассмотрим векторное поле, линейно зависящее от координат x и y:
.
Как и предположили, направление совпало с отрицательным направлением оси z. В данном случае ротор является константой, так как он независим от координаты. Количество вращения в приведенном выше векторном поле одно и то же в любой точке (x,y). График ротора F не слишком интересен:
Более сложный пример
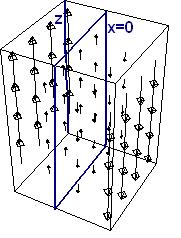
Теперь рассмотрим несколько более сложное векторное поле:
.
Ротор F с плоскостью x=0, выделенной темно-синим цветом
Три общих примера
Рассмотрим пример ∇ × [ v × F ]. Используя прямоугольную систему координат, можно показать, что
Если v и ∇ поменять местами:
что является фейнмановской записью с нижним индексом ∇F, что значит, что градиент с индексом F относится только к F.
Другой пример ∇ × [ ∇ × F ]. Используя прямоугольную систему координат, можно показать, что:
что можно считать частным случаем первого примера с подстановкой v → ∇.