что такое ромб в геометрии 8 класс определение
Ромб. Свойства и признаки ромба
Ромб – это параллелограмм, у которого все стороны равны.
Если у ромба – прямые углы, то он называется квадратом.
Свойства ромба
1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
Помимо этого:
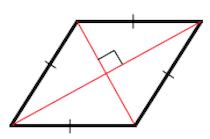
2. Диагонали ромба перпендикулярны.
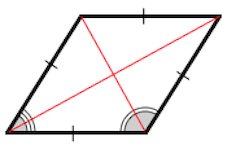
3. Диагонали ромба являются биссектрисами его углов.
4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Признаки ромба
Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:
1. Все стороны параллелограмма равны между собой ().
2. Диагонали пересекаются под прямым углом ().
3. Диагонали параллелограмма являются биссектрисами его углов.
Площадь ромба
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Ромб. Формулы, признаки и свойства ромба
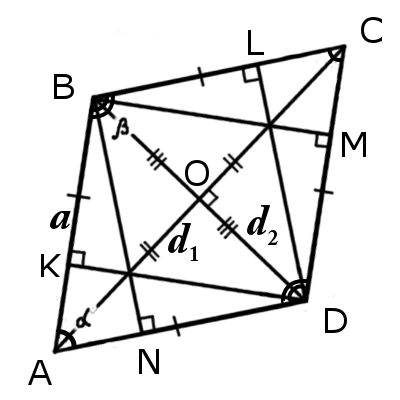 | 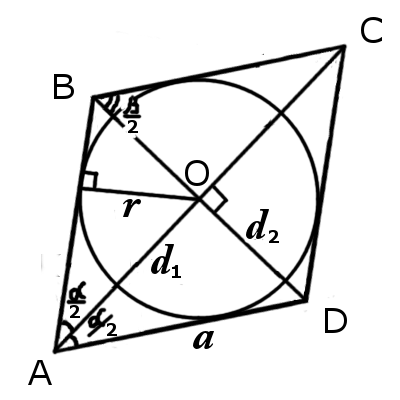 |
| Рис.1 | Рис.2 |
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
Сторона ромба
Формулы определения длины стороны ромба:
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 2 = a √ 2 + 2 · cosβ
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
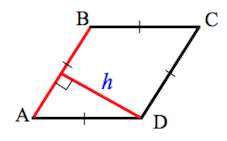
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Что такое ромб: определение, свойства, признаки
В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.
Определение ромба
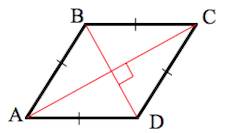
Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).
Примечание: квадрат является частным случаем ромба.
Свойства ромба
Свойство 1
Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.
Свойство 2
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.
Свойство 3
Диагонали ромба являются биссектрисами его углов.
Свойство 4
Сторону ромба a можно найти через его диагонали d1 и d2 (согласно теореме Пифагора).
Свойство 5
В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Радиус вписанной в ромб окружности r вычисляется по формуле:
Признаки ромба
Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:
Примечание: Любой четырехугольник, стороны которого равны, является ромбом.
Ромб, свойства, признаки, формулы, площадь и периметр
Ромб, свойства, признаки, формулы, площадь и периметр.
Ромб – это параллелограмм, у которого все стороны равны.
Ромб (определение и понятие):
Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе – «бубен») – это параллелограмм, у которого все стороны равны.
Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.
Ромбы отличаются друг от друга размером углов и длиной стороны.

Свойства ромба:
1. Противолежащие стороны ромба равны, т. к. все стороны ромба равны.
2. Противолежащие стороны ромба попарно параллельны.

3. Соседние углы ромба дополняют друг друга до 180°. Иными словами, сумма углов, прилежащих к любой из сторон ромба, равна 180°.
4. Диагонали ромба взаимно перпендикулярны.
5. Диагонали ромба точкой пересечения делятся пополам.
7. Диагонали ромба являются биссектрисами его углов и делят углы пополам.
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
8. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре.
9. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Признаки ромба:
Параллелограмм ABCD является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий:
– если две смежные стороны параллелограмма равны (отсюда следует, что все стороны равны), то он является ромбом.
AB = BC, то AB = BC = CD = AD;
– если диагонали параллелограмма пересекаются под прямым углом, то он является ромбом.
– если одна из диагоналей параллелограмма делит содержащие её углы пополам, то он является ромбом.
∠BAC = ∠CAD или ∠ABD = ∠DBC или ∠BCA = ∠ACD или ∠ADB = ∠BDC;
– если в параллелограмм можно вписать круг, то он является ромбом;
– если диагонали делят параллелограмм на четыре равных прямоугольных треугольника, то он является ромбом.
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Геометрические фигуры. Ромб.
Ромб рассматривают как вид параллелограмма, с двумя смежными равными сторонами либо с взаимно перпендикулярными диагоналями, либо с диагоналями делящими угол на 2 равные части.
Свойства ромба.
1. Ромб – это параллелограмм, поэтому противоположные стороны имеют одинаковую длину и параллельны попарно, АВ || CD, AD || ВС.
4. Сумма квадратов диагоналей равняется квадрату стороны, умноженному на четыре (вывод из тождества параллелограмма).
Признаки ромба.
Параллелограмм ABCD будет называться ромбом только в случае выполнения хотя бы одного из условий:
1. 2 его смежные стороны имеют одинаковую длину (то есть, все стороны ромба равны, AB=BC=CD=AD).
2. Угол пересечения диагоналей прямой (AC⊥BD).
3. 1-на из диагоналей делит углы, которые ее содержат пополам.
Пусть мы заранее не знаем, что четырёхугольник оказывается параллелограммом, однако известно, что все его стороны равны. Значит этот четырёхугольник является ромбом.
Симметрия ромба.
Ромб симметричен относительно всех своих диагоналей, зачастую его используют в орнаментах и паркетах.
Периметр ромба.
Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры. У периметра та же размерность величин, что и у длины.
Периметр ромба равняется сумме четырех длин его сторон либо произведению длины всякой из его стороны на 4 (т.к. у ромба все стороны равны).