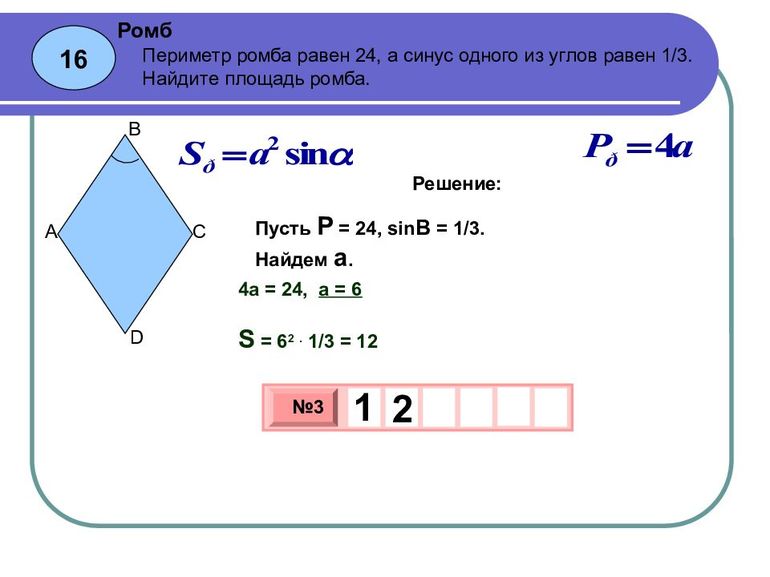
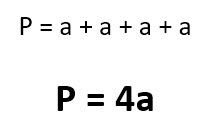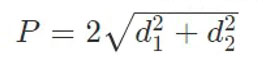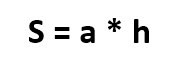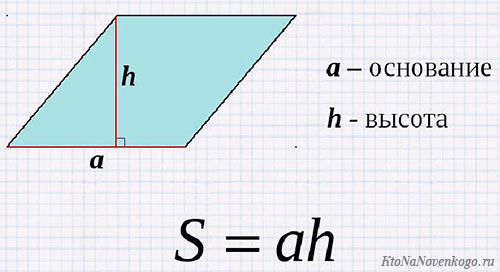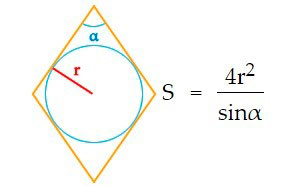что такое ромб определение и его свойства

Что такое ромб определение и его свойства

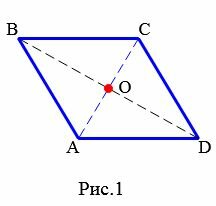
Определение 1. Ромб − это параллелограмм, у которого все стороны равны.

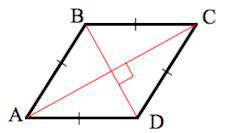
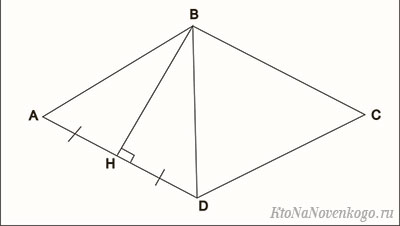
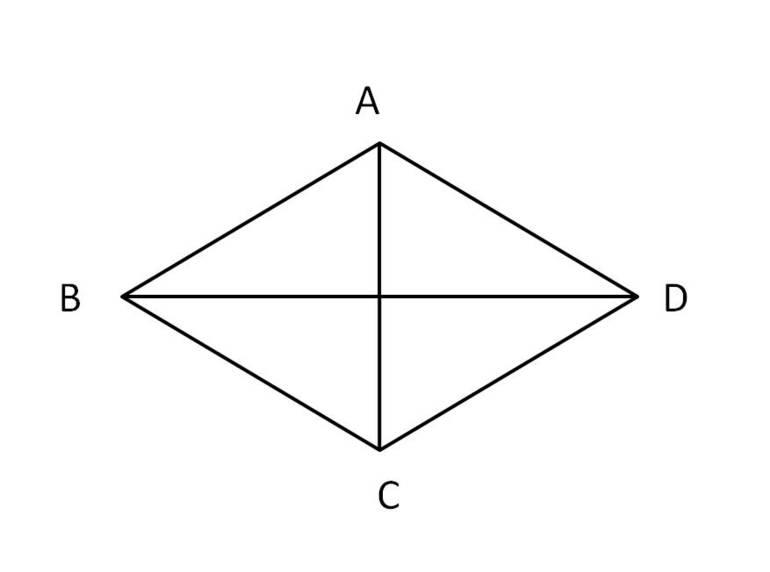
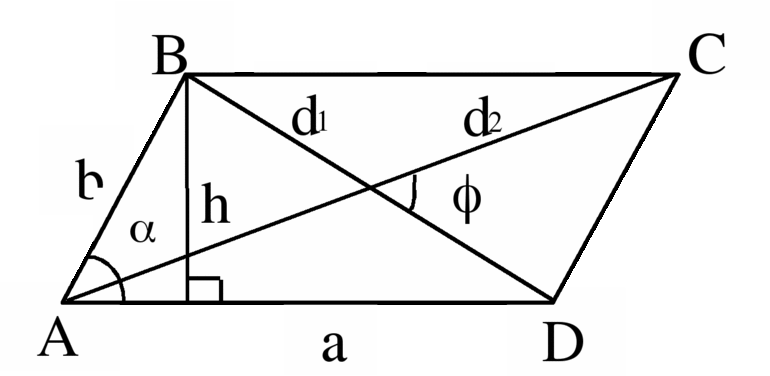
На рисунке 1 изображен ромб ABCD.

Определение 2. Ромб − это четырехугольник, у которого все стороны равны.

Ромб разделяет плоскость на две части, одна из которых называется внутренней областью ромба, а другая внешней областью ромба.

Объединение ромба и ограниченной им части плоскости также называют ромбом.

Свойства ромба

Поскольку ромб является параллелограммом, то имеет следующие свойства:

Ромб имеет также и следующие свойства:

Докажем свойства 6 и 7, сформулировав следующую теорему:

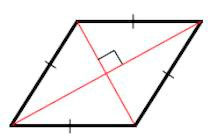
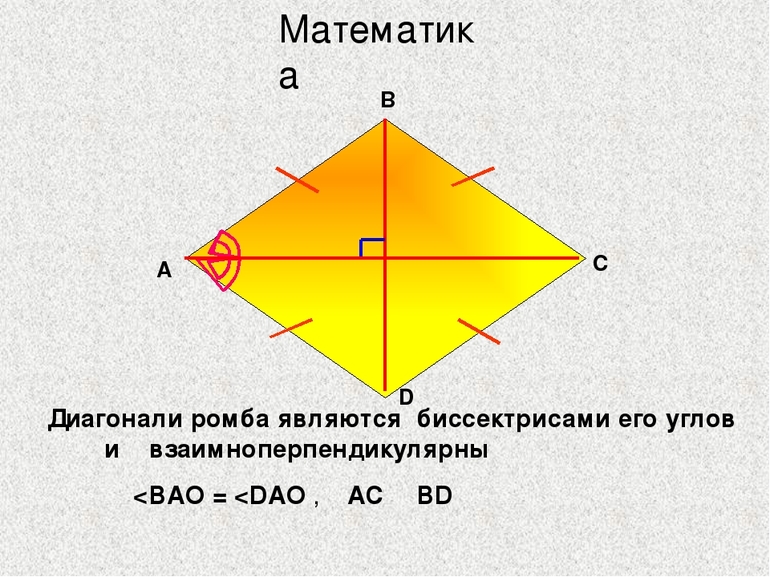
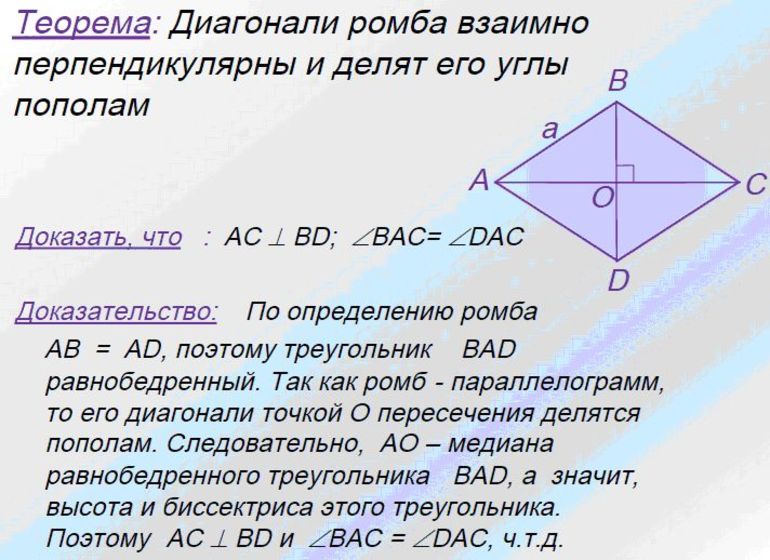
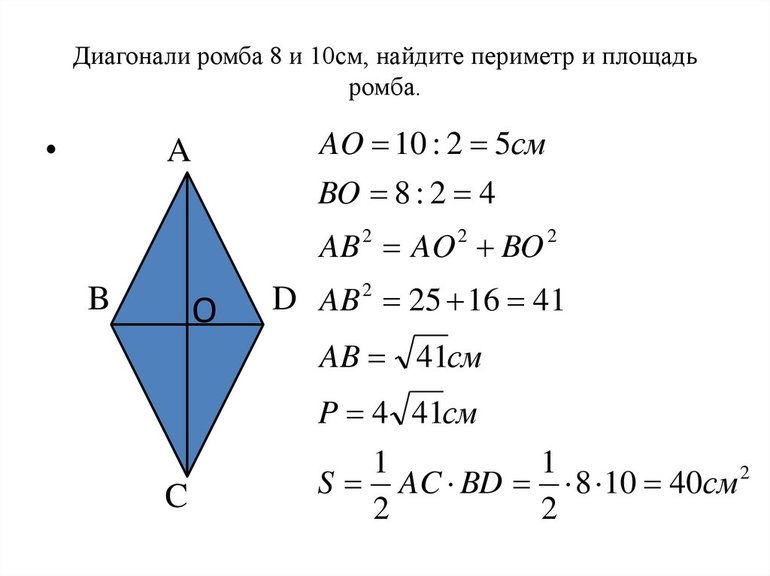
Теорема 1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Доказательство. По определению 1, \( \small AD = DC \) (Рис.2). Следовательно треугольник \( \small DAC \) равнобедренный. Тогда \( \small \angle DCO = \angle DAO. \) Учитывая, что \( \small AO = OC \) (свойство 5 ромба), получим, что треугольники \( \small DOA \) и \( \small DOC \) равны по двум сторонам и углу между ними (см. статью Треугольники. Признаки равенства треугольников). Тогда равны углы DOC и DOA. Но эти углы смежные и их сумма равна 180°. Следовательно \( \small \angle DOC= \angle DOA=90°. \) То есть диагонали AC и BD перпендикулярны.

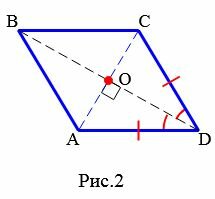Из равенства треугольников \( \small DOA \) и \( \small DOC \) также следует, что \( \small \angle CDO= \angle ADO,\) следовательно BD является биссектрисой угла ADС, то есть BD является биссектрисой ромба ABCD.

Признаки ромба

Признак 1. Если смежные стороны параллелограмма равны, то этот параллелограмм − ромб.

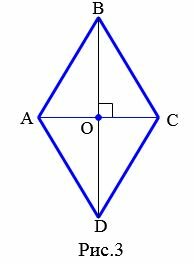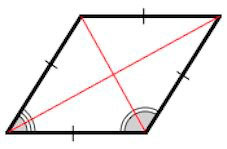
Доказательство. Пусть смежные стороны параллелограмма ABCD равны. То есть имеем: AB=BC (Рис.3). У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда DC=AB=BC=AD. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм − ромб.

Доказательство. Пусть диагонали параллелограмма ABCD перпендикулярны (Рис.3). Рассмотрим прямоугольные треугольники AOB и COB. Так как у параллелограмма диагонали точкой пересечения разделяются пополам (Свойство 2 статьи Параллелограмм), то AO=OC. Тогда прямоугольные треугольники AOB и COB равны по двум катетам (AO=OC, BO общий катет (см. статью Прямоугольный треугольник. Свойства, признаки равенства)). Следовательно AB=BC. Тогда по признаку 1 этот параллелограмм является ромбом.

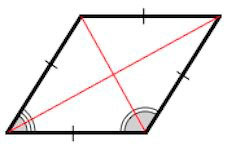
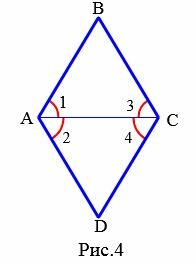
Признак 3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм − ромб.

Признак 4. Если стороны четырехугольника равны, то этот четырехугольник − ромб.

Доказательство. Пусть у четырехугольника все стороны равны. Тогда этот четырехугольник является параллелограммом (признак 2 статьи Параллелограмм). А по определению 1, этот параллелограмм является ромбом.

Источник

Ромб – между параллелограммом и квадратом

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы расскажем о такой геометрической фигуре, как РОМБ. Многие наверняка знают, как он выглядит.

Особенно спортивные болельщики, так как эмблемы многих команд связаны именно с ромбом. Тут достаточно вспомнить одну из главных российских команд – Спартак. Вот так она выглядит.

Ромб — это.

А вот как звучит официальное определение ромба:

История возникновения самого слова весьма примечательна. На древнегреческом оно звучит как «ῥόμβος», а на латыни «rombus». И переводятся оба слова как «бубен».

Дело в том, что в Древней Греции делали барабаны и прочие ударные инструменты чаще именно такой формы. Просто натягивать ткань на параллелограмм было гораздо проще. А вот круглые, более привычные нам сегодня барабаны появились позже.

И еще один интересный факт – карточная масть «бубны» называется так точно по той же причине.

Говоря об определении РОМБА, не лишним будет тогда сказать и что такое параллелограмм, раз он там фигурирует.

Параллелограмм – это геометрическая фигура, которая представляет собой четырехугольник, у которого противоположные стороны равны между собой и параллельны друг другу.

Выглядит классический параллелограмм вот так:

Впервые его описал знаменитый древнегреческий математик Евклид в своей книге «Начала». Это произведение вышло в 300 году до нашей эры. И было посвящено основам математики, которые были известны на то время.

В частности, Евклид в своей книге разделил все четырехугольники на две большие категории – параллелограмм и трапеция (так как у нее две стороны не параллельны друг другу). Также в «Началах» Евклид указал, что ромб является частным случаем параллелограмма, так как у него противоположные стороны равны.

И наконец, частным случаем самого ромба является квадрат. У него противоположные стороны не только равны, но еще и пересекаются под прямым углом.

Признаки ромба

Чтобы понять, что перед нами ромб, должно выполняться всего лишь одно из трех простых условий:

И тут будет не лишним подтянуть теоретическую базу и напомнить, что такое диагональ, и уж тем более что такое биссектриса.

Диагональ – это отрезок, который соединяет две любые вершины в многоугольнике, которые не находятся рядом друг с другом.

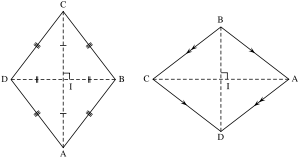
Если говорить конкретно о четырехугольнике, которым является и ромб, то диагональ соединяет две противоположные вершины и никак иначе. И таких диагоналей в ромбе две:

На этом рисунке диагоналями являются отрезки AC и BD. И как показано, они пересекаются под прямым углом, о чем и говорится во втором признаке ромба.

Биссектриса – это линия, которая выходит из угла и делит его ровно на две части.

Кстати, само слово «биссектриса» имеет латинские корни. Оно состоит из двух половин – «bi» (двойное) и sectio (разрезание).

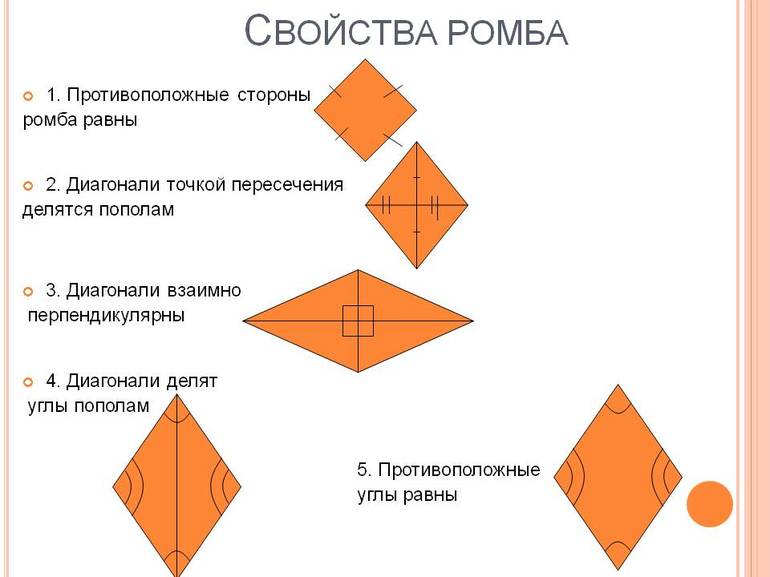
Свойства ромба

А можно все и перевернуть таким образом. Если вы точно определи, что перед вами ромб, то тогда для этой фигуры будут характерны вот такие свойства:

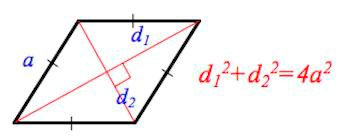
И есть еще одно свойство, которое помогает решать различные задачки на уроках геометрии. Оно звучит так:

Сумма квадратов обеих диагоналей ромба равна квадрату его сторону, умноженному на четыре.

Периметр ромба

Чтобы определить периметр любого четырехугольника, надо просто сложить между собой длины всех его сторон.

В случае с ромбом это совсем просто, так как они все равны между собой. И тогда формула для вычисления периметра получается такой:

Как несложно догадаться, буква «а» здесь – это длина стороны ромба.

Есть еще одна формула для вычисления периметра ромба – через диагонали. Она более сложная, но при решении различных задач вполне может и пригодиться.

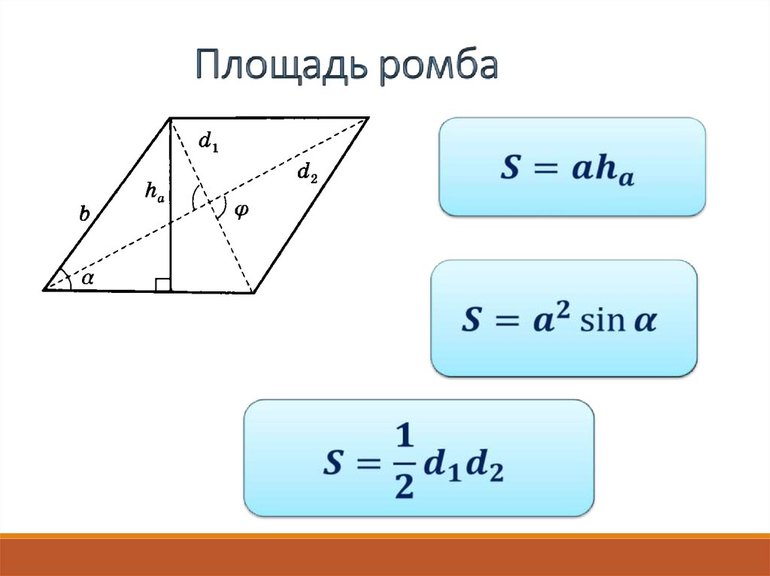
Площадь ромба

Площадь любой геометрической фигуры – это размер пространства, заключенного в границы этой самой фигуры.

Классическая формула для расчета площади ромба – через длины стороны и высоты.

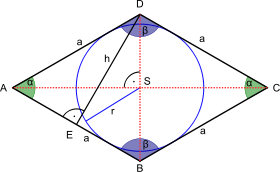
Главное, надо напомнить, что такое высота. Это отрезок, проведенный из вершины геометрической фигуры под прямым углом к противоположной стороне.

Она обозначается буквой «h» или «H» и выглядит вот так:

И наконец, формула для расчета площади ромба через сторону и высоту:

Есть и другие формулы для расчета площади ромба:

Вот и все, что мы хотели рассказать о ромбе.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Со временем, разница между квадратом, ромбом и параллелограммом забывается. То, что было само собой разумеющимся в школе, теперь кажется чем-то новым!:) Кстати, во времена СССР, именно ромб был самой популярной фигурой в дизайне всевозможных логотипов.

Источник

Общие сведения

Ромб является четырехугольником. В геометрии существует несколько видов последних. Для каждой фигуры предусмотрены свои соотношения, теоремы и формулы. Кроме того, математики выделяют специализированные алгоритмы, позволяющие точно и без ошибок определить тип фигуры.

Ученые разработали алгоритм для обучения, позволяющий за короткий промежуток времени перейти к решению сложных математических упражнений без каких-либо финансовых вложений. Он состоит из следующих элементов:

Изучение любой фигуры начинается всегда с ее определения, поскольку на основании этого возникают базовые знания.

Определение и частный случай

Ромбом называется параллелограмм с эквивалентными друг другу сторонами. О последнем можно сказать, что он относится к правильным четырехугольникам. Термин «правильный» означает равенство сторон одному значению. Следует отметить, что частным случаем ромба является квадрат, поскольку у него также имеются равные стороны. Эти фигуры имеют похожие свойства и формулы, однако некоторые соотношения отличаются.

Следовательно, необходимо правильно идентифицировать фигуру. Такая операция выполняется на основании признаков. Они присущи только конкретной фигуре и позволяют точно определить ее тип. Многие путают два ключевых понятия в геометрии: свойства и признаки. В учебниках существует множество определений, но, к сожалению, не все они понятны для новичков.

Признаками искомой фигуры называются характеристики, которые присущи только ей. Свойства — следствия из определений и доказательств теорем, используемые при доказательстве тождеств, утверждений и решения задач. Следует также обратить внимание на использование очередности. Первыми применяются признаки, а затем свойства.

Основные признаки

Признаки состоят из двух групп. Их формирование связано с количеством фигур, с которыми можно перепутать ромб. Определение последнего раскрывает их не полностью. Следовательно, математики для детального анализа разработали некоторый алгоритм, или первую группу. Различиями между искомой фигурой и параллелограммом являются следующие:

Семь признаков отсеивают параллелограмм, но не дают провести разделение между ромбом и квадратом (прямоугольником), поскольку два последних также попадают под них. Для этого случая математики также разработали специальный алгоритм, который заключается в следующем:

Если у фигуры внутренние углы являются прямыми, то он является квадратом (прямоугольником). Кроме того, вокруг квадрата можно описать окружность. Алгоритмы идентификации являются очень простыми и надежными, поскольку вероятность ошибки эквивалентна нулевому значению. Существуют и другие методики определения типа фигуры, но они считаются сложными. Следовательно, на начальных стадиях обучения не рассматриваются.

Примером одной из них является операция интегрирования, основанная на вычислении размерностей (площадей) и объемов тел вращения, которые получаются в результате вращения ромба вокруг своей оси. Эти характеристики отличаются от характеристик параллелограмма и квадрата.

Свойства фигуры

Ромб является частным случаем параллелограмма и имеет все свойства, которые присущи этой фигуре. Новички не берут их во внимание, что приводит к увеличению объемов вычислений, а также возникновению ошибок. Свойствами параллелограмма являются следующие:

Следует отметить, что свойства ромба присущи только ему. К ним относятся следующие:

Все свойства были получены математиками при доказательствах различных теорем. Для некоторых также были использованы вспомогательные утверждения. Например, для второго применялась теорема Пифагора.

Теорема о свойствах диагоналей

Математики рекомендуют рассмотреть теорему о свойствах диагоналей ромба, которая гласит, что диагонали искомой фигуры пересекаются в одной точке и взаимоперпендикулярны, а также являются биссектрисами его углов. Для доказательства утверждения следует его разделить на две части: взаимоперпендикулярность диагоналей и последние являются биссектрисами углов фигуры.

Необходимо начертить ромб ABCD со стороной «a», провести диагонали m1 (большую) и m2 (меньшую). Отметить их точку пересечения P. Существует много доказательств этого утверждения. Специалисты рекомендуют всегда выбирать самое простое, поскольку такой прием ценится на экзаменах. Одним из примеров рационального использования знаний является построение прямой в декартовой системе координат.

Согласно аксиоме геометрии, чтобы провести прямую, достаточно двух точек. Следовательно, нет смысла использовать 5, 10 и 20 элементов, поскольку все эти действия приведут к одному результату. Методика доказательства упрощенного типа считается самой эффективной. Следует рассмотреть треугольники ABC и ADC, полученные в результате проведения диагонали m1. Для удобства в геометрии слово «треугольник» заменяется символом «Δ», а угол — «∠». Они равны между собой по трем сторонам, то есть боковые стороны равны a (стороны ромба), а общая — эквивалентна значению диагонали m1.

Следует отметить, что они также являются равнобедренными, поскольку их боковые стороны равны между собой, то есть AB = BC = a и AD = CD = a. Далее следует обратить внимание на малую диагональ m1. Она опущена из вершины B и D на сторону AC. Исходя из свойства медианы в равнобедренном Δ, m1 является высотой и биссектрисой, то есть справедливо такое уравнение ∠ABC = ∠ADC = ∠ABP + ∠CPB = ∠APD + ∠CPD. Кроме того, высоты BP и DP образуют перпендикуляр со стороной AC.

Утверждение доказывается аналогично для ΔABC и ΔADC. Они равны по трем сторонам (AD = DC и AB = BC, а также по общей стороне BD) и являются равнобедренными, исходя из свойств сторон ромба. Диагональ m1 проходит через эти Δ. Она также является медианой, биссектрисой и высотой. Теорема доказана полностью.

Основные соотношения

Для решения задач применяются формулы. Ромб не является исключением. Соотношения применяются для определения неизвестных параметров фигуры. Однако бывают случаи, когда недостаточно одной формулы, поскольку нужно связать несколько компонентов в единый процесс вычислений. Для корректного использования формул следует ввести класс некоторых обозначений:

Периметр и площадь

Периметр ромба — характеристика, которая эквивалентна значению алгебраической суммы всех ее сторон. Площадью называется параметр геометрической фигуры, показывающий ее размерность в определенном геометрическом пространстве. Следует отметить, что величина S существует только у фигуры в двумерном пространстве. В трехмерном нужно рассматривать объем геометрического тела. Кроме того, у объемного тела есть параметр площади поперечного сечения. Эта величина является двумерной.

Периметр вычисляется по следующей формуле: P = 4 * a. Следует отметить, что величину a можно выражать через диагонали, площадь и другие характеристики. Базовая формула площади ромба имеет такой вид: S = a * BP = a * DP = a * AP = a * CP. Кроме того, размерность можно найти по следующим соотношениям:

В последней формуле при большем значении диагонали m1 следует брать тангенс острого угла, а при m2 — тангенс тупого угла. На это нужно обратить особое внимание, поскольку на этом моменте новички делают много ошибок, путая диагонали и углы.

Нахождение стороны

Длина стороны находится очень просто, поскольку математики выполнили доказательства некоторых тождеств. Они предлагают готовые решения в виде формул, позволяющих правильно выразить одну величину через другую, и подставить необходимые числовые значения:

Необходимо обратить внимание, что используются в некоторых соотношения тригонометрические функции. Последнее соотношение является формулой определения периметра. Если он известен, то легко вычислить значение стороны, используя обратную формулу P.

Другие соотношения

Осталось еще два параметра ромба — диагонали. Специалисты рекомендуют воспользоваться готовыми соотношениями для нахождения ее длины:

m1 = [4 * a 2 — (m2)^2]^(½) = [4 * S — (m2)^2]^(½).

m2 = [4 * a 2 — (m1)^2]^(½) = [4 * S — (m1)^2]^(½).

Следует также рассмотреть случай, когда окружность вписана в ромб. Такой прием применяется для расширения возможностей поиска неизвестной, что существенно позволит сэкономить время на расчетах. К формулам относятся следующие тождества:

Если нужно найти диаметр, то следует использовать такое соотношение: R = D / 2. Можно также выразить диагонали через стороны. Для этого следует подставить вместо m1 значение со стороной a.

Таким образом, математики предлагают специальный алгоритм, позволяющие без ошибок идентифицировать ромб, а затем применить соответствующие формулы для решения задачи.

Источник

Что такое ромб определение и его свойства

Содержание

Этимология

Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Кстати, название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Свойства

Признаки

Параллелограмм является ромбом, если выполняется одно из следующих условий:

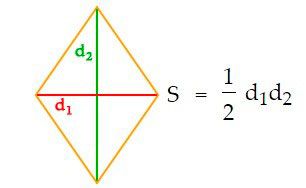
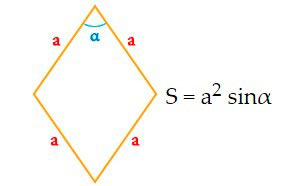
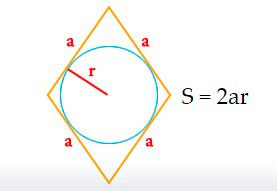
Площадь ромба

где — угол между двумя смежными сторонами ромба.

В геральдике

Червлёный ромб в серебряном поле

В червлёном поле 3 сквозных ромба: 2 и 1

Просверленный червлёный ромб в серебряном поле

В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

См. также

ПланигонСм. такжеТеория и практика: Принадлежность точки многоугольнику • Теорема Бойяи — Гервина • Теорема Брахмагупты • Теорема Гаусса — Ванцеля • Формула Пика • Теорема о сумме углов многоугольника

Полезное

Смотреть что такое «Ромб» в других словарях:

ромб — ромб, а … Русский орфографический словарь

ромб — ромб/ … Морфемно-орфографический словарь

РОМБ — (греч.). Равносторонний параллелограмм, с неравными углами, но равными сторонами. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. РОМБ греч. rhombos. Равносторонний четырехугольник, у которого два противоположные… … Словарь иностранных слов русского языка

ромб — а; м. [греч. rhombos] 1. Матем. Параллелограмм, все стороны которого равны. 2. В Красной Армии (до введения погон в 1943 г.): знак различия высшего командного состава, имевший такую форму. ◁ Ромбический, ая, ое. (1 зн.). Р ая форма. Кровать с… … Энциклопедический словарь

ромб — РОМБ, РОМБОС, РОМБУС а, м. rhombe m., нем. Rhombus <, лат. rhombus <гр. 1. Параллелограмм, все стороны которого равны. БАС 1. || О чем л., имеющем такую форму. БАС 1. У этого искусника <повара Полутыкина> ни одна морковка не попадала… … Исторический словарь галлицизмов русского языка

РОМБ — РОМБ, фигура на плоскости, четырехугольник с равными сторонами. Ромб частный случай ПАРАЛЛЕЛОГРАММА, у которого или две смежные стороны равны, или диагонали пересекаются под прямым углом, или диагональ делит угол пополам. Ромб с прямыми углами… … Научно-технический энциклопедический словарь

РОМБ — муж. равносторонний, косой четвероугольник, как бы сдвинутый набок квадрат. Ромбовые шашки, клетки, косые. Ромбоид муж. ромб; | толстый ромб, тело ромбоидное, ромбоидальное, косоугольная призма. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

Ромб (КА) — Ромб серия многоэлементных юстировочно кабровочных космических аппаратов, служащих для контроля точностных характеристик и разрешающей способности РЛС (систем СПРН, СККП, ПКО, ПРО) и для калибровки их каналов. Данные КА проводят точные… … Википедия

РОМБ — РОМБ, ромба, муж. (греч. rhombos). 1. Параллелограмм, все стороны которого равны. Квадрат частный случай ромба (мат.). 2. Равносторонний косоугольник в отличие от квадрата (разг.). 3. Знак различия, имеющий форму косоугольника (воен.). Толковый… … Толковый словарь Ушакова

РОМБ — РОМБ, а, муж. 1. В математике: параллелограмм, все стороны к рого равны. 2. Название высшего офицерского знака различия такой формы на петлицах в Красной Армии (с 1919 по 1943 г.). Р. в петлице. | прил. ромбический, ая, ое (к 1 знач.) и ромбовый … Толковый словарь Ожегова

РОМБ — (от греческого rhombos веретено), равносторонний параллелограмм … Современная энциклопедия

Источник