Релятивистское сокращение длины

Изучите эффект сокращения длины движущегося тела при релятивистской скорости: какая скорость релятивистской частицы, Лоренцево сокращение, формула и схема.

Перемещающиеся объекты подвержены сокращению длины вдоль размерности движения. Этот эффект приобретает значение только на релятивистских скоростях.

Задача обучения

Основные пункты

Термин

Релятивистское сокращение длины – физическое давление уменьшения длины, отмеченное наблюдателем для объектов с ненулевой скоростью. Оно появляется из-за того, что скорость света остается неизменной для любой системы отсчета. Рассмотрите примеры эффекта релятивистского сокращения длины при релятивистских скоростях.

Пример 1

Представьте простую конструкцию часов, представленную двумя зеркалами А и В, расположенных в вакуумных условиях. Между ними отражается световой импульс. Их разделение – L, а тактовые сигналы попадают в зеркало. Теперь вообразим, что часы пребывают в позиции покоя. Время для перехода импульса из А к В высчитывается по формуле:

(c – скорость света).

Теперь часы начали перемещаться в горизонтальной направленности по отношению к стационарному наблюдателю. Световой импульс исходит из зеркала А. Наблюдателю кажется, что у светового импульса присутствует более длинный путь, потому что, когда свет приблизится к В, часы сдвинутся в горизонтальной направленности. То есть, мы увидим:

Это иллюстрация пути, по которому свет должен пройти, когда часы пребывают в позиции покоя

Это иллюстрация пути, по которому должен пройти свет, когда часы перемещаются

Пример 2

В системе отсчета с движением относительно часов, механизм будет функционировать медленнее. Теперь давайте определим длину линейки. В этом случае вы будете перемещаться со скоростью v. Можно математически вычислить показатель в системе отсчета, если умножить свою скорость на потраченное время: L’ = vt’. Если кому-то в системе покоя нужно вычислить длину линейки, то нужно повторить те же действия: L = vt. В системе отсчета смещается линейка, поэтому t длиннее t’. То есть, в вашей системе отсчета линейка кажется короче.

В повседневных скоростях эффект сокращения длины не учитывается. Но его замечают при весомой части световой скорости. Сокращение происходит в направленности, параллельной стороне движения тела.

Длина объекта в позиции покоя на разных скоростях

Пример 3

Возьмем скоростной показатель в 13400000 м/с, а длина – 99% от длины в состоянии покоя. На скорости в 423000000 м/с показатель все еще достигает 99%. Так как величина скорости приближается к световой, то эффект доминирует. В виде формулы:

где L₀ – собственная длина, L – длина в относительном движении относительно объекта, v – относительная скорость между наблюдателем и перемещающимся объектом, с – скорость света. Коэффициент Лоренца определяется как:

В последней формуле предполагают, что объект располагается параллельно линии перемещения. Для наблюдателя перемещающийся близко к световой скорости объект будет приближаться к 0.

Источник

Фантазии о физической причине лоренцева сокращения, объясняющей инвариантность скорости света и пр

Всем известно об инвариантности скорости света в любой инерциальной системе отсчёта, но наука пока не может объяснить физику, т.е. природу механизма этого феномена.

Математическая же модель явления постулирует, что все процессы протекают в 4-х мерном пространстве-времени, в котором феномены СТО следуют из сохранения интервала событий при преобразованиях вращения системы координат. Вряд ли можно отрицать, что реальность как бы натягивают на математические конструкции. Причём то, что в оных почти сплошь важную роль играют мнимые числа, в реальности непредставимые, нисколько не умаляет успехов науки. Ещё Э.Мах говорил, что объяснения излишни, если наблюдаемые феномены хорошо описываются формулами. И не будем с этим эмпириокритицизмом спорить.

Математики изобретают абстракции и примеряют их к реальности. Отсюда Сингулярность, кротовые норы и пр. экзотика. А может стоит пофантазировать, например и о том, что изменится в наших представлениях о мире, если бы причиной лоренцева сокращения был некий гипотетически предполагаемый физический механизм. Почему бы нет?

1.Физическая причина лоренцева сокращения

Сначала выскажу такую, как бы очевидную, сентенцию, что частицы, атомы, молекулы взаимодействуют между собой посредством физических полей. Можно, конечно сказать, что они обмениваются квантовыми частицами, но мы сейчас играем на поле релятивистской теории, поэтому пока забудем о квантах. Итак, первое фантастическое допущение состоит в том, что именно благодаря взаимоуравновешиванию полевых воздействий частицы складываются в определённую конфигурацию и образуют тела. Если какая-то частичка отклонится от положения равновесия, то от неё побежит полевое возмущение, которое сдвинет остальные частицы, что, в свою очередь вызовет обратное полевое воздействие от них на эту частицу.

И, второе допущение, это что полевое возмущение распространяется в некоем общем пространстве с некоей определённой скоростью. А фантастичность этого допущения в том, что по науке поле существует само по себе в 4-х мерном пространстве-времени (П-В) и ни по чему не распространяется. В общем, сложно по науке… Мы предположим, что поля распространяются и существуют в едином 3-х мерном пространстве – в котором находимся мы, Земля и звёзды. Вроде бы сиё само собой разумеется и кто ж этого не знает, однако посмотрим что получится. Кому не интересно заморачиваться с формулами, могут ограничиться чтением только выделенного текста.

Итак, соглашаемся, что между частицами существует время взаимодействия, которое складывается из времени прихода к ним возмущения и времени возвращения отклика от них обратно. А в результате постепенно снова установится прежняя конфигурация тела.
Рис.1 Полевые воздействия, определяющие положение частицы
Для любой точки тела можно выделить группы точек, с которыми у неё будут равные времена взаимодействия и которые назовём изохронными с данной точкой. Ситуация отражена на рис.1. Естественно, что в покое сфера любого радиуса R _покоя вокруг точки является геометрическим местом точек (ГМТ) изохронных с ней.

Заметим, что движение частицы в каждый момент определяется суммой равнодействующих сил, которые прикладываются одновременно от совокупности всех изохронных с ней групп частиц. Попытаемся выяснить как изменится при движении тела поверхность ГМТ, образуемая совокупностью точек 2, 3 и т.д. с одинаковыми временами взаимодействия с точкой 1, которая может уже и не быть сферой.
Пусть точки 1 и 2 тела взаимно неподвижны и синхронно движутся вправо со скоростью V. Когда точка 1 находится в начале координат, посылается полевое возмущение к точке 2. Взаимное расположение точек при этом отмечено литерой A.
Рис.2 Схема полевых взаимодействий точек тела — туда и обратно
Когда возмущение достигнет точки 2, она пройдёт расстояние V∙t₁. Позиции точек при этом отмечены литерой B. За время возврата возмущения от точки 2 к точке 1, точка 2 пройдёт расстояние V∙t₂. Их новые позиции отмечены литерой C.

Формулы (1) описывают по теореме Пифагора расстояния на рис.2, а полученные из них (2) являются уравнениями для вычисления времён t₁ и t₂, значения которых даются формулами (3) и (4) для положительных значений корней, где β=V/c.

Формула (5) даёт значение времени взаимодействия от посылки возмущения до получения отклика.

Из (5) получим уравнение (6) для координат x и y геометрического места изохронных точек, с которыми одинаково время взаимодействия точки 1.
Формула (6) описывает эллипсоид, показанный на рис.3, сжатый вдоль направления движения (вдоль оси X) в √(1 ‑ β 2 ) раз, то есть соответственно формуле Лоренца. Точка 2 на поверхности сферы в покое, при движении сдвинется в положение 2′. При этом материальные точки, бывшие изохронными с точкой 1 в покое, останутся изохронными с ней и при движении.
Рис.3
Итак, при движении материальный объект сжимается по Лоренцу именно потому, что сжимается сама «картинка» физических полей обеспечивающая его целостность в пространстве.

Так как лоренцево сокращение одинаково для всех изохронных точек окружающих каждую точку объекта, то весь движущийся объект одинаково пропорционально сократится вдоль оси движения.

2.Вывод формулы замедления времени

Определим время взаимодействия при движении объекта по сравнению с временем взаимодействия в покое.
Формулы (7) связывают координаты точек при движении с их же координатами при покое в соответствии с
уравнением (6). В формуле (8) вычисляется время взаимодействия при покое. Формулы (9) и (10) получены из формулы (6) при подстановке в неё значений координат x и y и R_покоя из формул (7). Формула (11) эквивалентна (10). Формула (12), полученная из (11) при подстановке в неё левой части формулы (8), связывает времена взаимодействий при покое и при движении. В традиционной форме это отображено в формуле (13), где T₀ обозначен интервал времени между событиями в покоящемся объекте, а T – это интервал времени между теми же событиями в движущемся теле.
Итак, времена взаимодействия всех точек в движущемся объекте увеличиваются в одинаковой пропорции по Лоренцу по сравнению с временем взаимодействия при покое. Соответственно, вообще все процессы в движущемся объекте реально замедляются в таком же отношении.
Причину замедления времени легко понять, если учесть, что возмущение поля от задней из взаимодействующих частиц должно будет догонять переднюю по ходу движения. Когда скорость тела почти сравняется со скоростью света, догонять придётся долго, а при скорости тела равной скорости света, оно её не догонит никогда. Все изменения в теле прекратятся и время в нём как бы остановится.

3.Объяснение феномена постоянства скорости света и пр.

В собственной системе поезда для этого же t₀ мы имеем соотношение t₀ = S₀/c₀. Но поскольку поперечные размеры при движении не изменяются, т.е. S = S₀, получаем, что и c₀ = c.
Полагаю не нужно доказывать постоянство измеренной скорости света для произвольной ориентации луча, что лишь добавило бы неоправданной сложности. Считая доказанным инвариантность скорости света, нетрудно вывести и преобразования Лоренца (ПЛ), причём без какой-либо апелляции к уравнениям Максвелла или к математически абстрактному пространству Минковского.

4.Вывод преобразований Лоренца

Событие состоит в прибытии светового импульса в точку «E«, находящуюся в неизменных координатах x’ и y’ в системе отсчёта , движущейся со скоростью V относительно неподвижной ИСО , посланного в момент, когда точки O и O’ обеих СО совпадали.
Рис.6.

В собственной СО длине L, измеренной в СО , будет соответствовать координата x’. Для события справедлива система уравнений (1), решая которую получим (2), а затем (3) и (4).
Поскольку длины тел при движении сжимаются по Лоренцу, а скорость света, как доказано в гл.3, одинакова в любой СО, то для собственных x’ и t’ в СО справедливы соотношения (5). Подставив соотношения из (5) в (3) получим (6), а подставив их в (4) получим (7). В силу относительности движения можно считать движущейся систему , но тогда в (6) и (7) надо нештрихованные переменные заменить штрихованными, а скорость V следует взять с обратным знаком, либо просто решить систему относительно x и t.
В результате получим выражения (8) для канонического вида преобразований Лоренца координат и времени событий в разных ИСО.
При использовании ПЛ как чисто формального математического метода, физический механизм феноменов СТО остаётся непроявленным. Поэтому в моих предыдущих статьях о релятивистских эффекте Доплера и аберрации света, а также законах отражения от движущегося наклонного зеркала, ПЛ принципиально не использовались с целью демонстрации именно физической причины этих феноменов.

5.Обоснование принципа относительности и ограничения его применимости

Отметим, что если в покое на схеме рис.1 возмущение от точки 1 до ГМТ изохронных с нею точек приходило одновременно, то при движении, на схеме рис.2, это уже не выполняется. В каждой точке этого ГМТ отклик на возмущение будет создаваться в разные времена, но сойдутся они в точке 1 одновременно. Вопрос в том, будет ли результат от этого такой же как и в покое?

Выше было доказано, что в любой ИСО измеренные собственные времена и расстояния между всеми точками будут такие же, как в покое. Следовательно и количество периодов, например инициированной электромагнитной волны, между любыми точками будет таким же, как и в покое. Поскольку возмущение поля произвольной конфигурации может быть представлено разложением по ряду монохроматических гармоник, то соответственно конфигурации и напряжённости всех полей в собственной системе будут одинаковы им же при покое. Следовательно фазовые соотношения и синхронизация полей, образующих тело, не нарушаются, и все процессы в нём будут протекать как и при покое.

Именно это и провозглашает эйнштейновский «принцип относительности», и, как видим, он математически неизбежно выводится из двух допущений (см. гл.1), напомню: первое: что положение вещественных частиц определяется структурой полей, и второе, что распространение полей происходит с конечной скоростью.

То есть принцип относительности уже как бы вовсе и не априори всеобщий принцип, а следствие, и имеет понятные границы применимости. В частности, скорость света имеет смысл не мировой константы, а является конкретной скоростью света в конкретной области пространства. И кое-где может быть иной вследствие взаимодействия с местными физическими полями, например, гравитацией. Итак, имеем две альтернативы, которые имеют результатом совершенно одинаковые релятивистские формулы:

Поэтому продолжим фантазировать дальше.

6.Вывод формулы E = Mc² и уравнений динамики

Сначала выясним, как преобразуются силы при релятивистских скоростях. Выделим в теле элемент объёма, на который действуют уравновешенные моменты сил. При движении тела продольный размер (вдоль траектории движения) выделенного элемента сократится в соответствии с коэффициентом Лоренца. Чтобы элемент остался в равновесии, точно в таком же соотношении должны увеличиться силы, перпендикулярные движению.
Рис.7.
Величина сил параллельных движению не изменится. Фактор зависимости сил от ориентации относительно направления движения следует учитывать при векторном разложении сил в следующих ниже формулах.

Заметим, что разгон тела до некоей скорости осуществляется приложенной силой, которая соответственно при том выполняет некую работу, чем увеличивает энергию тела. А чем в пространстве отличается разогнанное тело от находящегося в покое? Тем, что разогнанное сжато по Лоренцу. В гл.1 выводится формула для геометрического места точек (ГМТ), окружающих данную точку, с которой у них одинаково время взаимодействия физических полей. Это ГМТ оказывается эллипсоидом сжатым по Лоренцу в направлении движения. Обратим теперь внимание на то, что объём W этого эллипсоида уменьшается пропорционально лоренцеву сокращению. Это отражено в формуле (1) ниже. Вот теперь сделаем уже действительно фантастическое предположение, что при ускорении тела работа силы затрачивается на сжатие занимаемого им объёма пространства, который остаётся затем неизменным при свободном движении. По крайней мере, это предположение ничем не хуже научных сентенций, что пространство может искривляться или раздуваться.

Предположим, что эта энергия E обратно пропорциональна объёму, до которого его удалось сжать согласно формуле (2), или (3) после подстановки в неё (1).
E из (3) разложим в ряд Тейлора (4), откуда (5) – приращение энергии от скорости в первом приближении при малых скоростях. Но при малых скоростях оно же равно (6). Сравнивая (5) и (6), получим (7) и (8). Подставляя (8) в (3), получим (9), связывающее энергию тела в сжатом пространстве с его массой покоя.
Релятивистскую массу выразим формулой (10), откуда, подставляя (2), получим известное выражение (11), связывающее массу и энергию. Сравнивая (9) и (11), получим (12).
Масса является просто иной формулировкой энергии затраченной на сжатие пространства. И в этом смысле они эквивалентны. А вещество всего лишь «маркирует» занимаемый телом участок пространства.

Изменение полной энергии E системы, т.е. энергии сжатия пространства, в полном соответствии с ньютоновой классической механикой, равно работе приложенной силы как произведению силы на путь, а изменение импульса P системы равно произведению той же силы на время её действия. Эти зависимости отражены в формулах (13). После подстановки в них выражений для энергии из (11) и импульса P из формулы (14) получаем систему уравнений (15), которая в форме малых приращений записана в (16) в векторной форме. Затем, дифференцируя по времени, запишем систему дифференциальных уравнений (17), описывающих релятивистскую динамику. Силу F дифференцировать не надо, так как она внешняя и не зависит от вариаций переменных системы. Подставив в формулу (A) выражение для массы из (12), получим известную релятивистскую формулу прямолинейного движения (18).
Из системы уравнений (17) можно выяснить зависимость массы от скорости. Подставив F из формулы (B) в формулу (A) и разделив обе части равенства на c², при ускорении вдоль траектории движения, получим выражения (19) и (20). Откуда, интегрируя, получим выражение (21). Легко видеть, что оно эквивалентно прологарифмированному выражению (12) для релятивистской массы, где const равна логарифму от массы покоя m₀. Это значит, что именно такая зависимость массы от скорости обеспечивает соответствие энергии Mc² и импульса M·V, в формулах (16, 17). И отсюда также следует, что величина, принятая нами ранее за массу покоя, является не зависящей от скорости константой, как это и записано в исходных формулах (9). И значит верно наше предположение о зависимости энергии от степени сжатия пространства.

Конечно заявление о сжатии пространства не слишком убедительно. Если пространство предполагается пустым вместилищем частиц и тел, то как можно сжать пустоту? Пустота так и останется пустотой. Наука, правда, позволяет себе говорить об искривлении пустого пространства – формулы того требуют. Однако, строго говоря, её пространство является математической абстракцией.

Но мы вполне обоснованно можем предположить, что пространство не пусто, а заполнено некоей материей, которая, предположим, не в сжатом состоянии воспринимается нами как пустота. Когда же, например, она находится под напряжением сжатия, мы имеем вещественные частицы и тела. Когда оные в ней покоятся, то степень сжатия (энергия) участка этой материи соответствует массе покоя тела, а при его ускорении увеличивается и степень сжатия (энергия) тела, и соответствующая ему масса.

И вот в этой материальной среде вполне могут существовать и распространяться с конкретной скоростью физические поля определяющие местоположение и взаимодействие частиц (вплоть до «самых-самых» первичных – которые, продолжаем фантазировать, окажутся явлением фокусировки полей от окружающей их обстановки без которой они и не существуют), энергия покоя и движения которых определяется степенью сжатия занимаемого ими участка первоматерии. Собственно, уравнения релятивистской динамики как раз и описывают движение этих неоднородностей напряжений (вещественных тел) в первоматерии. Как мы могли видеть, при этом никаких противоречий с опытом Майкельсона и преобразованиями Лоренца не возникает.

Источник

Сокращение длины и другие релятивистские эффекты

В статье рассматриваются сокращение длины и другие релятивистские эффекты, вытекающие из преобразований Лоренца-Эйнштейна. Показывается, что сокращению длины тел в движущейся системе координат должно соответствовать такое же сокращение интервалов времени в той же системе, иначе не выполняется принцип постоянства скорости света, как его сформулировал Эйнштейн. Вместе с тем показывается, что сокращению длины должно соответствовать такое же уменьшение массы тел в той же системе координат. Обосновывается вывод о том, что в действительности никакие релятивистские эффекты не существуют.

“Релятивистское” сокращение длины и замедление времени

Рис.1. Стержень AB покоится в системе X ’ O ’ Y ’

t ’ = ( t – vx /c 2 ) / (1- v 2 / c 2 ) 1/2 (4)

x ’, y ’, z ’ и t ’ – параметры после преобразования.

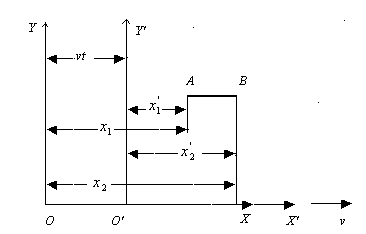
Длину стержня AB можно определить как разность координат его концов, измеряемых в одной и другой системе координат. Тогда на основании (1) можно записать:

x ’ 1 = ( x 1 – vt ) / (1- v 2 / c 2 ) 1/2

x ’ 2 = ( x 2 – vt ) / (1- v 2 / c 2 ) 1/2

l ’ = l / (1- v 2 / c 2 ) 1/2 или l = l ’ (1- v 2 / c 2 ) 1/2 (5)

Р.Фейнман в [2] так объясняет сокращение длины:

Имея в виду подобного рода “доказательства”, Гегель в своей “Науке логики” написал примерно следующее: “. софистика есть рассуждение из необоснованной предпосылки, принимаемой без критики и необдуманно. Чем богаче определенностью, а тем самым и отношениями становятся мысли, тем. более запутанным и лишенным смысла становится их изображение в таких формах, как числа. Символика является иногда. удобным средством обойтись без того, чтобы охватить, указать, оправдать определения понятий ” (подчеркнуто мной – В.П).

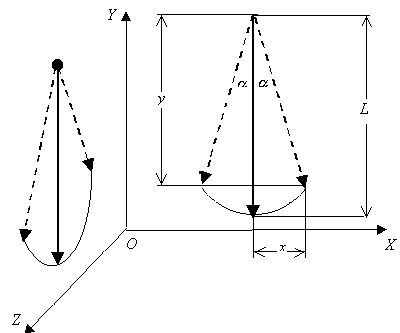
Предположим теперь, что в движущейся системе координат установлены двое совершенно одинаковых часов таким образом, что маятник одних часов колеблется в плоскости, параллельной направляю движения этой системы, а маятник вторых часов колеблется в плоскости, перпендикулярной движению системы (рис.2):

Рис.2. Часы в движущейся системе координат.

l / c = l ’(1- v 2 / c 2 ) 1/2 / c

l ’(1- v 2 / c 2 ) 1/2 / = t ’/ (1- v 2 / c 2 ) 1/2

l ’(1- v 2 / c 2 ) 1/2 / t ’/ (1- v 2 / c 2 ) 1/2 ]

l ’ / t ’ (1- v 2 / c 2 ) = c ’,

Объясняя “неукам”, что такое сокращение длины, лауреат Нобелевской премии по физике Л.Купер в [3] пишет: “Еще более странным оказалось бы измерение расстояний, поскольку наблюдатель в S ’ вынужден был бы считать, что его измерительные стержни и масштабные линейки сократились в направлении движения в (1- v 2 / c 2 ) 1/2 раз. Если он начнет рисовать окружность, он вынужден рисовать кривую, представленную на рисунке 3:

Рис.3. Это окружность, а не овал

Наблюдатель, конечно, понимает, что его окружность выглядит довольно странно. Однако при том определении длины, которую ему пришлось ввести (по настоянию Лоренца-Эйнштейна – В.П.), именно такая кривая обладает требуемым свойством, что все ее точки равноудалены от центра”. Т.е. он должен предположить, что кривая линия, которую он нарисовал, есть окружность! Однако этот же наблюдатель может сообразить, что, поворачивая нарисованную им кривую вокруг своей длинной оси, он может добиться того, что его фигура рано или поздно будет выглядеть именно как окружность! Это произойдет тогда, когда плоскость фигуры окажется ориентированной перпендикулярно его движению, что противоречит принципу относительности, как его сформулировал Эйнштейн. Таким образом, приходим к выводу, что сокращение длины противоречит принципу относительности. К счастью, предложенная Эйнштейном формула сложения скоростей обращает выражение (1- v 2 / c 2 ) 1/2 в 1, что исключает и сокращение длины, и замедление времени, но зато возвращает нас к принципу относительности, как его сформулировал Эйнштейн.

.

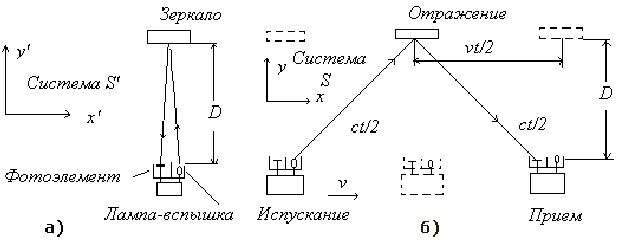
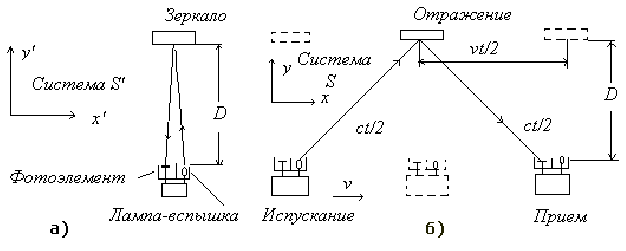
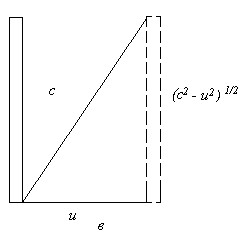
Рис.4. Опыт со “световыми” часами
а – “световые” часы покоятся в системе S ’
б – те же часы, движущиеся через систему S ; ( c 2 – v 2 ) 1/2

Рис.4в. Диагональ, по которой движется пучок света в движущихся “световых” часах

Как было показано выше, сокращение длины в сочетании с замедлением времени не обеспечивает выполнение принципа постоянства скорости света, поэтому нужно отнестись к “объяснениям” Р.Фейнмана весьма внимательно.

Прежде всего, обратим внимание, что в этом эксперименте имеется два наблюдателя: внешний, как его определил Р.Фейнман, относительно которого часы движутся с некоторой скоростью, и второй – космонавт, который движется вместе с часами. Рассмотрим ход лучей в часах с точки зрения каждого из наблюдателей.

Очевидно, утверждение, что “пучок света” движется по диагонали, означает, что по диагонали движется каждый отдельно излученный импульс света, из которых и состоит пучок. При объяснении своего эксперимента Майкельсон считал, что отклонение перпендикулярного луча, наблюдаемое неподвижным наблюдателем, обусловлено аберрацией. В действительности, однако, это не так: известно, что аберрация возникает в результате движения приемника света относительно источника, тогда как в этом эксперименте и приемник, и источник неподвижны друг относительно друга. Следовательно, аберрация в данном случае оказывается совершенно не при чем.

[ D 2[1] + ( uτ ) 2 ] 1/2 = ( c 2 + u 2 ) 1/2 τ

D 2 + u 2 τ 2 = c 2 τ 2 + u 2 τ 2

Таким образом, время движения перпендикулярного луча света оказывается одинаковым и с точки зрения космонавта, и с точки зрения внешнего, как его определил Р.Фейнман, наблюдателя. Это значит, что движущиеся световые часы идут точно так же, как и неподвижные. И никакого замедления времени!

Известно, что ход лучей в своем эксперименте Майкельсон рассматривал с точки зрения внешнего, неподвижного наблюдателя, относительно которого интерферометр движется с орбитальной скоростью. По мнению Майкельсона, отклонение светового луча вслед за смещением интерферометра, наблюдаемым неподвижным наблюдателем, обусловлено аберрацией. Однако, аберрация возникает при движении приемника относительно источника света. В эксперименте же Майкельсона источник света – полупрозрачное зеркало – неподвижен относительно приемника – отражателя. Следовательно, аберрация в данном эксперименте оказывается совершенно не при чем. Как показано в [3], и в этом эксперименте отклонение луча вслед за смещением интерферометра, наблюдаемое неподвижным наблюдателем, обусловлено сложением скорости света, движущегося в атмосфере Земли, со скоростью движения самой атмосферы, движущейся с орбитальной скоростью Земли. В этом случае, время движения каждого из лучей, движущихся в интерферометре, оказывается одинаковым равным 2 l / c (где l – расстояние между зеркалами) как с точки зрения земного наблюдателя, неподвижного относительно интерферометра, так и с точки зрения внешнего, неподвижного, наблюдателя, относительно которого интерферометр движется со скоростью орбитального движения Земли. Пусть это не соответствует СТО, но зато соответствует действительности.

Таким образом, нулевой результат эксперимента Майкельсона-Морли обусловлен исключительно отсутствию движения интерферометра относительно той среды, в которой распространяется света в этом эксперименте, т.е. воздуха, или атмосферы Земли, тогда как в эксперименте Саньяка, в котором интерферометр движется относительно окружающего его воздуха, интерференционная картина в точности соответствует скорости этого движения [4]. Вместе с тем, эксперимент Саньяка подтверждает, что движущиеся относительно окружающей среды “световые” часы идут медленнее таких же часов, неподвижных относительно той же среды, однако это является свойством таких и только таких часов и не является свойством самого времени.

О движении “релятивистских” мюонов

В результате мюоны могут достигать поверхности Земли прежде, чем они распадутся” [5].

Известно, что в момент образования все мюоны имеют приблизительно одинаковую массу, тогда как у поверхности Земли обнаруживаются мюоны с самыми различными массами, в том числе и с массами, равными массе мюонов в момент их образования. Если отдельно посчитать количество мюонов с массой, равной массе мюонов в момент их образования, то окажется, что количество таких мюонов в точности соответствует количеству, рассчитанному по формуле

где N 0 – количество частиц в данном объеме в момент времени t ;

N – количество частиц в том же объеме в момент времени T ;

T – период полураспада частиц).

Избыток мюонов у поверхности Земли наблюдается за счет мюонов, имеющих массу, отличную от массы мюонов в момент их образования. Возникает вопрос, каким образом у поверхности Земли оказались эти мюоны, если в момент образования все мюоны имели одинаковую массу? Ответ может быть только один – эти мюоны образовались в результате распада других, более массивных мюонов. И действительно, на различных высотах над поверхностью Земли обнаруживаются мюоны с самыми различными массами [6].

Предположим, что распадается мюон с массой, равной 207 массам электрона – это масса мюона “в состоянии покоя”, т.е. масса мюона, движущегося с относительно небольшой скоростью, когда “релятивистскими” эффектами можно пренебречь. При распаде такого мюона образуется электрон с массой, равной массе одного электрона.

Согласно закону сохранения импульса, импульс системы до распада должен быть равен импульсу системы после распада:

где M – масса мюона, равная 207 массам электрона;

v – скорость мюона “в состоянии покоя”;

m – масса электрона, образовавшегося в результате распада мюона;

V – скорость электрона.

Таким образом, увеличение количества мюонов, наблюдаемых у поверхности Земли, не связано с изменением периода их полураспада. Период полураспада мюонов, как и любых других частиц, не зависит от состояния их движения. Следовательно, возникновение и распад мюонов не могут служить достоверными доказательствами “релятивистского” замедления времени.

“Релятивистское” увеличение массы движущихся тел

m = m 0 / (1 – v 2 / c 2 ) 1/2 (7)

где R – радиус основания цилиндра;

m = m 0 π R 2 L (1 – v 2 / c 2 ) 1/2

Т.е. масса тела уменьшится пропорционально уменьшению его длины. Ранее мы отмечали, что сокращению длины тел (расстояний) в движущейся системе координат должно соответствовать такое же сокращения интервалов времени между двумя событиями, произошедшими в той же системе координат, иначе не получается принцип постоянства скорости света, как его сформулировал Эйнштейн.. Теперь же мы пришли к выводу, что если сокращение длины движущихся тел действительно имеет место в действительности, то сокращению длины тел должно соответствовать такое же уменьшение его массы, так как уменьшение длины тела приводит к уменьшению его объема.

Однако, вопреки здравому смыслу, сторонники СТО утверждают, что наблюдения увеличения массы движущихся тел соответствует именно увеличение их массы. При этом имеется в виду многократно повторенный один и тот же опыт с движением электрически заряженных частиц в электромагнитных полях ускорителей различных конструкций. Известно, что цель этих экспериментов заключалась в увеличении массы (энергии) частиц, движущихся в электромагнитных полях этих ускорителей. Какова же была действительная скорость ускоряемых частиц и насколько величина этой скорости соответствовала формуле (7) заинтересовал только одного человека – Бертоцци, который исследовал движение электронов в электрическом поле линейного ускорителя [7,8]. Бертоцци пришел к выводу, что увеличение энергии ускоряемых электронов происходит при постоянной скорости их движения и что это увеличение зависит исключительно от напряженности электрического поля ускорителя и длины пути, пройденному электронами в этом поле.

Таким образом, формула (7), описывающая увеличение массы движущихся тел в зависимости от скорости их движения, не соответствует действительности.

Приведенные выше рассуждения позволяют заключить следующее:

Источник