что такое рекурсивный алгоритм

Рекурсия и рекурсивные алгоритмы

Цель лекции: изучить понятие, виды рекурсии и рекурсивную триаду, научиться разрабатывать рекурсивную триаду при решении задач на языке C++.

Рекурсия – это определение объекта через обращение к самому себе.

Рекурсивный метод в программировании предполагает разработку решения задачи, основываясь на свойствах рекурсивности отдельных объектов или закономерностей. При этом исходная задача сводится к решению аналогичных подзадач, которые являются более простыми и отличаются другим набором параметров.

На этапе параметризации из постановки задачи выделяются параметры, которые описывают исходные данные. При этом некоторые дальнейшие разработки решения могут требовать введения дополнительных параметров, которые не оговорены в условии, но используются при составлении зависимостей. Необходимость в дополнительных параметрах часто возникает также при решении задач оптимизации рекурсивных алгоритмов, в ходе которых сокращается их временная сложность.

Выделение базы рекурсии предполагает нахождение в решаемой задаче тривиальных случаев, результат для которых очевиден и не требует проведения расчетов. Верно найденная база рекурсии обеспечивает завершенность рекурсивных обращений, которые в конечном итоге сводятся к базовому случаю. Переопределение базы или ее динамическое расширение в ходе решения задачи часто позволяют оптимизировать рекурсивный алгоритм за счет достижения базового случая за более короткий путь обращений.

Декомпозиция представляет собой сведение общего случая к более простым подзадачам, которые отличаются от исходной задачи набором входных данных. Декомпозиционные зависимости описывают не только связь между задачей и подзадачами, но и характер изменения значений параметров на очередном шаге. От выбранных отношений зависит трудоемкость алгоритма, так как для одной и той же задачи могут быть составлены различные зависимости. Пересмотр отношений декомпозиции целесообразно проводить комплексно, то есть параллельно с корректировкой параметров и анализом базовых случаев.

Анализ трудоемкости рекурсивных алгоритмов методом подсчета вершин дерева рекурсии

Рекурсивные алгоритмы относятся к классу алгоритмов с высокой ресурсоемкостью, так как при большом количестве самовызовов рекурсивных функций происходит быстрое заполнение стековой области. Кроме того, организация хранения и закрытия очередного слоя рекурсивного стека являются дополнительными операциями, требующими временных затрат. На трудоемкость рекурсивных алгоритмов влияет и количество передаваемых функцией параметров.

Важной характеристикой рекурсивного алгоритма является глубина рекурсивных вызовов – наибольшее одновременное количество рекурсивных обращений функции, определяющее максимальное количество слоев рекурсивного стека, в котором осуществляется хранение отложенных вычислений. Количество элементов полных рекурсивных обращений всегда не меньше глубины рекурсивных вызовов. При разработке рекурсивных программ необходимо учитывать, что глубина рекурсивных вызовов не должна превосходить максимального размера стека используемой вычислительной среды.

Будем использовать следующие обозначения для конкретного входного параметра D :

R(D) – общее число вершин дерева рекурсии,

R_V(D) – объем рекурсии без листьев ( внутренние вершины ),

R_L(D) – количество листьев дерева рекурсии,

H_R(D) – глубина рекурсии.

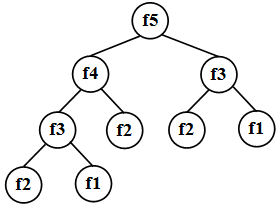
Тогда полное дерево рекурсии для вычисления пятого члена последовательности Фибоначчи будет иметь вид ( рис. 34.1):

Характеристиками рассматриваемого метода оценки алгоритма будут следующие величины.

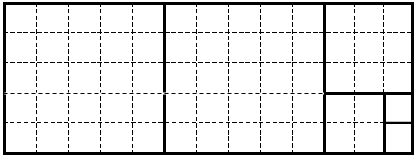
Пример 1. Задача о разрезании прямоугольника на квадраты.

Разработаем рекурсивную триаду.

База рекурсии: для m=n число получившихся квадратов равно 1, так как данный прямоугольник уже является квадратом.

Характеристиками рассматриваемого метода оценки алгоритма будут следующие величины ( рис. 34.3).

Источник

Как работает рекурсия – объяснение в блок-схемах и видео

Представляю вашему вниманию перевод статьи Beau Carnes How Recursion Works — explained with flowcharts and a video.

«Для того чтобы понять рекурсию, надо сначала понять рекурсию»

Рекурсию порой сложно понять, особенно новичкам в программировании. Если говорить просто, то рекурсия – это функция, которая сама вызывает себя. Но давайте попробую объяснить на примере.

Представьте, что вы пытаетесь открыть дверь в спальню, а она закрыта. Ваш трехлетний сынок появляется из-за угла и говорит, что единственный ключ спрятан в коробке. Вы опаздываете на работу и Вам действительно нужно попасть в комнату и взять вашу рубашку.

Вы открываете коробку только чтобы найти… еще больше коробок. Коробки внутри коробок и вы не знаете, в какой из них Ваш ключ. Вам срочно нужна рубашка, так что вам надо придумать хороший алгоритм и найти ключ.

Есть два основных подхода в создании алгоритма для решения данной проблемы: итеративный и рекурсивный. Вот блок-схемы этих подходов:

Какой подход для Вас проще?

В первом подходе используется цикл while. Т.е. пока стопка коробок полная, хватай следующую коробку и смотри внутрь нее. Ниже немного псевдокода на Javascript, который отражает то, что происходит (Псевдокод написан как код, но больше похожий на человеческий язык).

В другом подходе используется рекурсия. Помните, рекурсия – это когда функция вызывает саму себя. Вот второй вариант в псевдокоде:

Оба подхода выполняют одно и тоже. Основный смысл в использовании рекурсивного подхода в том, что однажды поняв, вы сможете легко его читать. В действительности нет никакого выигрыша в производительности от использования рекурсии. Порой итеративный подход с циклами будет работать быстрее, но простота рекурсии иногда предпочтительнее.

Поскольку рекурсия используется во многих алгоритмах, очень важно понять как она работает. Если рекурсия до сих пор не кажется Вам простой, не беспокойтесь: Я собираюсь пройтись еще по нескольким примерам.

Граничный и рекурсивный случай

То, что Вам необходимо принять во внимание при написании рекурсивной функции – это бесконечный цикл, т.е. когда функция вызывает саму себя… и никогда не может остановиться.
Допустим, Вы хотите написать функцию подсчета. Вы можете написать ее рекурсивно на Javascript, к примеру:

Эта функция будет считать до бесконечности. Так что, если Вы вдруг запустили код с бесконечным циклом, остановите его сочетанием клавиш «Ctrl-C». (Или, работая к примеру в CodePen, это можно сделать, добавив “?turn_off_js=true” в конце URL.)

Рекурсивная функция всегда должна знать, когда ей нужно остановиться. В рекурсивной функции всегда есть два случая: рекурсивный и граничный случаи. Рекурсивный случай – когда функция вызывает саму себя, а граничный – когда функция перестает себя вызывать. Наличие граничного случая и предотвращает зацикливание.

И снова функция подсчета, только уже с граничным случаем:

То, что происходит в этой функции может и не быть абсолютно очевидным. Я поясню, что произойдет, когда вы вызовете функцию и передадите в нее цифру 5.

Сначала мы выведем цифру 5, используя команду Console.Log. Т.к. 5 не меньше или равно 1, то мы перейдем в блок else. Здесь мы снова вызовем функцию и передадим в нее цифру 4 (т.к. 5 – 1 = 4).

Мы выведем цифру 4. И снова i не меньше или равно 1, так что мы переходим в блок else и передаем цифру 3. Это продолжается, пока i не станет равным 1. И когда это случится мы выведем в консоль 1 и i станет меньше или равно 1. Наконец мы зайдем в блок с ключевым словом return и выйдем из функции.

Стек вызовов

Рекурсивные функции используют так называемый «Стек вызовов». Когда программа вызывает функцию, функция отправляется на верх стека вызовов. Это похоже на стопку книг, вы добавляете одну вещь за одни раз. Затем, когда вы готовы снять что-то обратно, вы всегда снимаете верхний элемент.

Я продемонстрирую Вам стек вызовов в действии, используя функцию подсчета факториала. Factorial(5) пишется как 5! и рассчитывается как 5! = 5*4*3*2*1. Вот рекурсивная функция для подсчета факториала числа:

Теперь, давайте посмотрим что же происходит, когда вы вызываете fact(3). Ниже приведена иллюстрация в которой шаг за шагом показано, что происходит в стеке. Самая верхняя коробка в стеке говорит Вам, что вызывать функции fact, на которой вы остановились в данный момент:

Заметили, как каждое обращение к функции fact содержит свою собственную копию x. Это очень важное условие для работы рекурсии. Вы не можете получить доступ к другой копии функции от x.

Нашли уже ключ?

Давайте кратенько вернемся к первоначальному примеру поиска ключа в коробках. Помните, что первым был итеративный подход с использованием циклов? Согласно этому подходу Вы создаете стопку коробок для поиска, поэтому всегда знаете в каких коробках вы еще не искали.

Но в рекурсивном подходе нет стопки. Так как тогда алгоритм понимает в какой коробке следует искать? Ответ: «Стопка коробок» сохраняется в стеке. Формируется стек из наполовину выполненных обращений к функции, каждое из которых содержит свой наполовину выполненный список из коробок для просмотра. Стек следит за стопкой коробок для Вас!

И так, спасибо рекурсии, Вы наконец смогли найти свой ключ и взять рубашку!

Вы также можете посмотреть мое пятиминутное видео про рекурсию. Оно должно усилить понимание, приведенных здесь концепций.

Заключение от автора

Надеюсь, что статья внесла немного больше ясности в Ваше понимание рекурсии в программировании. Основой для статьи послужил урок в моем новом видео курсе от Manning Publications под названием «Algorithms in Motion». И курс и статься написаны по замечательной книге «Grokking Algorithms», автором которой является Adit Bhargava, кем и были нарисованы все эти замечательные иллюстрации.

И наконец, чтобы действительно закрепить свои знания о рекурсии, Вы должны прочитать эту статью, как минимум, еще раз.

От себя хочу добавить, что с интересом наблюдаю за статьями и видеоуроками Beau Carnes, и надеюсь что Вам тоже понравилась статья и в особенности эти действительно замечательные иллюстрации из книги A. Bhargav «Grokking Algorithms».

Источник

Рекурсивный алгоритм

Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.

Другими словами, рекурсия — способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Рекурсия используется, когда можно выделить самоподобие задачи.

Определение в логике, использующее рекурсию, называется индуктивным (см., например, Натуральное число).

Содержание

Примеры

Алгоритм по передвижению башни, алгоритм передвинет нужное количество дисков из пирамиды «источник» на пирамиду «задание» используя «запасную» пирамиду.

Если число дисков равно одному, тогда:

В противном случае:

Рекурсия в программировании

Функции

Мощь рекурсивного определения объекта в том, что такое конечное определение способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за этот счёт работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что рекурсивные вызовы не бесплатны — на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивают выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. К сожалению, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Lisp), описание которого содержит все необходимые сведения.

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

Рекурсия в физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

Рекурсия в лингвистике

Способность языка порождать вложенные предложения и конструкции. Базовое предложение кошка съела мышь может быть за счет рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)

Цитаты

Итерация от человека. Рекурсия — от Бога. — Л. Питер Дойч [1]

Большая часть всех шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода. Известные высказывания: ‘Чтобы понять рекурсию, нужно сначала понять рекурсию’, ‘Чтобы что-то сделать, надо что-то сделать’, ‘Для приготовления салата необходимы: огурцы, помидоры, салат’. Весьма популярна шутка о рекурсии, напоминающая словарную статью:

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

Русская народная сказка-песня «У попа была собака…» являет пример рекурсии:

Источник

Что такое рекурсивный алгоритм

3. Подводные камни рекурсии

3.3. Третий камешек (в адрес косвенной рекурсии)

4. Классификация типов рекурсии (Роботландия)

4.1. Прямая рекурсия

4.2. Косвенная рекурсия

4.3. Терминальные и нетерминальные рекурсии

4.3.1. Терминальные рекурсии

4.3.2. Нетерминальные рекурсии

4.4. Конечная и бесконечная рекурсия

4.4.1. Бесконечная прямая терминальная рекурсия

4.4.2. Конечная прямая терминальная рекурсия

4.4.3. Конечная прямая нетерминальная рекурсия

4.5. Примеры рекурсивных картин

1.1. Определение

Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.

Часто рекурсия сильно упрощает программирование, делая программу уди вительно короткой.

Сказанное совсем не означает, что рекурсия находится на задворках человеческой мысли. Рекурсия — мощный инструмент математики и, конечно, информатики. Часто рекурсивные описания настолько легки и красивы, на­сколько тяжелы и громоздки попытки обойтись циклами.

Посмотрите, например, как лаконично описывается при помощи рекурсии последовательность чисел Фибоначчи:

1.2. Числа Фибоначчи

Каждый элемент этой последовательности, начиная с третьего, равен сумме двух непосредственно предшествующих элементов. Первые два члена последовательности равны единице.

Эти числа являются решением задачи, которую итальянский математик Фибоначчи сформулировал в 1202 году:

«Каждый месяц самка из пары кроликов приносит двух детёнышей (самца и самку). Через два месяца новая самка сама приносит пару кроликов. Нужно найти число кроликов в конце года, если в начале года была одна новорождённая пара и в течение этого года кролики не умирали».

Ответ: к концу года число пар кроликов достигнет числа f (12) = 144, т. е. поголовье возрастет до 288 кроличьих единиц.

1.3. Подводные камни рекурсии

Рекурсия таит в себе подводные камни.

Использовать рекурсию разумно тогда, когда рекурсивна сама природа зада­чи. Искусственно построенная рекурсия (как альтернатива циклу) редко бы­вает оправдана. Например, для суммирования членов последовательности лучше применить цикл, а не рекурсию.

В чём заключается опасность рекурсии при машинных вычислениях? Дело в том, что при каждом рекурсивном вызове расходуется дополнительно часть машинной памяти (в ней сохраняются адреса возврата и локальные переменные процедур, если язык допускает использование переменных). При «глубоких» рекурсивных вызовах вся доступная память компьютера может быстро исчерпаться.

Но даже в некоторых естественно-рекурсивных задачах рекурсию использо­ вать не всегда разумно. В качестве примера рассмотрим упоминаемую ранее последовательность чисел Фибоначчи.

Каждое обращение к f ( n ) при п > 2 приводит к двум рекурсивным обращениям. Посмотрите, как быстро растёт число вызовов процедуры f при рекурсивном вычислении (рис).

Рис Рекурсивное нахождение числа Фибоначчи

Число рекурсивных вызовов растёт как степень двойки, т. е. быстрее, чем размножаются кролики! Заметим, правда, что «степенной» рост рекурсивного дерева f ( n ) не означает, что число вершин будет измеряться степенью двойки. Дерево не получится симметричным, некоторые ветви будут заканчиваться раньше других, и в итоге общее число вершин будет соответствовать именно числу Фибоначчи.

Числа Фибоначчи лучше вычислять при помощи цикла пока:

у:= 0 //у _ вспомогательная переменная

х:= х + у // суммируем два предыдущих значения

Рассматривать рекурсию как переход в начало процедуры неправильно: ведь рекурсия это не переход, а выполнение нового экземпляра процедуры.

1.3. Третий камешек (в адрес косвенной рекурсии)

Прямая рекурсия предпочтительнее косвенной. Косвенная рекурсия — это замаскированная форма прямой, и маскировка ухудшает читабельность программы, её отладку и сопровождение.

1.4. Классификация типов рекурсии (Роботландия)

Прямая и косвенная рекурсия

В математике и информатике рекурсивной называют такую функцию или процедуру, которая при работе обращается к себе самой, прямо или косвенно. Соответственно говорят о прямой и косвенной рекурсии.

При прямой рекурсии процедура вызывает себя в своём собственном теле, например:

Косвенная рекурсия образуется цепочкой процедур, и эта цепочка замыкается в рекурсивное кольцо, например:

Сама по себе косвенная рекурсия не содержит новых идей. Это другая форма записи прямой рекурсии, если, конечно, промежуточные процедуры не содержат дополнительных рекурсий.

Пример сложного переплетения косвенных рекурсий можно обнаружить в программе лексического анализатора. Однако эта сложность скрадывается предварительным построением диаграммы (таблицы) переходов.

Когда диаграмма построена, мы формально переводим её в программу, даже не задумываясь о том, сколько сложных косвенных рекурсий при этом монтируется в простой с виду программный код.

Это то самое исключение из правил, когда косвенная рекурсия не затрудняет понимание алгоритма работы программы.

выражение > ::- число > | выражение > + число >

Диаграмма переходов, соответствующая определению 1, показана на рис

На этой схеме изображены 4 состояния-процедуры: ответ, выражение, вход И ошибка.

Процедура ответ рекурсивной не является.

Процедура ошибка на схеме рекурсивной не показана, хотя алгоритм её ра­боты содержит прямую рекурсию с отложенной командой для перемещения исполнителя к месту обнаруженной ошибки.

Процедуры выражение и вход содержат вызов друг друга, значит, образуют цепочку косвенной рекурсии.

Диаграмма переходов, соответствующая определению 2, показана на рис. (на диаграмме не показаны переходы в состояние «ошибка» и не учтена проверка на баланс скобок на уровне всего выражения).

Посмотрите, какое здесь переплетение рекурсий!

Например, процедура вход содержит прямую рекурсию и одновременно две

Терминальные и нетерминальные рекурсии

Терминал — это оконечное устройство, концевик. В частности, терминалом называют монитор (часто вместе с клавиатурой) как оконечное устройство компьютера для диалога с пользователем. Раньше, когда использовали большие ЭВМ типа ЕС или БЭСМ, терминалы (монитор + клавиатура) выносили в отдельные залы, где несколько пользователей одновременно работали на своих терминалах с одной ЭВМ. Иногда такой терминал имел собственный процессор и небольшую память: получалось, что терминал — это небольшой компьютер. Но это не мешало ему быть терминалом, т. к. он работал не самостоятельно, а служил оконечным устройством другой ЭВМ.

Терминальная рекурсия — это рекурсия-концевик, т. е. такой рекурсивный вызов, после которого других команд в процедуре выполняться не должно. Понятно, что терминальная рекурсия может быть как прямой, так и косвенной.

Посмотрите на процедуры вход и выражение:

ЕСЛИ 0 ТО выражение

ИНАЧЕ ЕСЛИ 1 ТО добавить 1

ИНАЧЕ ЕСЛИ 2 ТО добавить2

ВПРАВО ЕСЛИ + ТО вход

ИНАЧЕ ЕСЛИ ПУСТО ТО ответ

В процедуре вход косвенная терминальная рекурсия обеспечивается вызовом процедуры выражение.

Обратите внимание на то, что запись:

ЕСЛИ 0 ТО выражение

ИНАЧЕ ЕСЛИ 1 ТО добавить 1

ИНАЧЕ ЕСЛИ 2 ТО добавить2

является одной условной командой в отличие от записи:

ЕСЛИ 0 ТО выражение

ЕСЛИ 1 ТО добавить1

ЕСЛИ 2 ТО добавить2

Последняя запись содержит три команды и, если бы именно так было записано в процедуре вход, рекурсивный вызов был бы уже нетерминальным, а следовательно, процедура вход работала бы совсем по-другому. Она содержала бы две «отложенные» в рекурсии команды:

ЕСЛИ 1 ТО добавить 1

ЕСЛИ 2 ТО добавить2 ИНАЧЕ ошибка

Типичный пример прямой нетерминальной рекурсии содержится в процедуре ошибка:

Нетерминальная рекурсия порождает отложенные команды, рекурсивные «пружинки».

Конечная и бесконечная рекурсия

Как цикл может быть конечным и бесконечным, так и рекурсия (это ведь тоже повторение!) может быть бесконечной или нет.

Для того чтобы бесконечных повторений (циклических или рекурсивных) было, нужна проверка на окончание.

Бесконечная прямая терминальная рекурсия

Кукарача кричит «Не могу» на правом краю поля.

Конечная прямая терминальная рекурсия

ЕСЛИ ПУСТО ТО поиск

Кукарача находит кубик с символом и останавливается.

Конечная прямая нетерминальная рекурсия

ЕСЛИ ПУСТО ТО поиск

Кукарача находит кубик с символом и возвращается на прежнее место.

1.5. Примеры рекурсивных картин

2. Подпрограмма-функция Гейн 8

Во-первых, подпрограмма-функция, как и любая подпрограмма, имеет имя, посредством которого к ней можно обратиться. Во-вторых, она имеет набор аргументов, которые описываются именами переменных. А вот переменной для результата у неё нет, поскольку вычисляемое ею значение всегда тут же присваивается переменной, указанной пользователем.

Чтобы воспользоваться подпрограммой-функцией, достаточно написать команду

Иногда для двух целых чисел, отличных от О, требуется найти их наибольший общий делитель, сокращённо НОД. Напомним, что наибольшим общим делителем двух ненулевых целых чисел называется такое целое число, которое делит каждое из этих чисел (т. е. является их общим делителем) и среди всех общих делителей является наибольшим. Легко понять, что наибольший общий делитель всегда является натуральным числом.

Составим подпрограмму-функцию, вычисляющую НОД для двух целых чисел.

(*Функция ABS находит абсолютное значение числа х*)

Сам алгоритм нахождения НОД двух целых чисел, который мы оформили в виде подпрограммы-функции, был предложен великим математиком древности Евклидом и носит его имя.

Таким образом, подпрограмма-функция является разновидностью вспомогательного алгоритма. Она удобна, когда результатом является одна величина, значение которой присваивается нужной переменной из основного алгоритма. Также подпрограмму-функцию можно рассматривать как новое допустимое действие исполнителя.

Источник