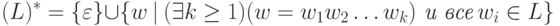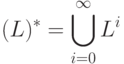что такое регулярный язык

Регулярный язык

Связанные понятия

В логике логи́ческими опера́циями называют действия, вследствие которых порождаются новые понятия, с использованием уже существующих. В более узком смысле, понятие логической операции используется в математической логике и программировании.

В математике (особенно в теории категорий), коммутативная диаграмма — изображаемая в наглядном виде структура наподобие графа, вершинами которой служат объекты определённой категории, а рёбрами — морфизмы. Коммутативность означает, что для любых выбранных начального и конечного объекта для соединяющих их ориентированных путей композиция соответствующих пути морфизмов не будет зависеть от выбора пути.

В теоретической информатике, точнее, в теории формальных языков, высота итерации — это мера структурной сложности регулярных выражений — высота итерации регулярного выражения равна максимальной глубине вложенности звёздочек, присутствующих в регулярном выражении.

В теории вероятностей случайная величина имеет дискретное равномерное распределение, если она принимает конечное число значений с равными вероятностями.

В теории алгоритмов классами сложности называются множества вычислительных задач, примерно одинаковых по сложности вычисления. Говоря более узко, классы сложности — это множества предикатов (функций, получающих на вход слово и возвращающих ответ 0 или 1), использующих для вычисления примерно одинаковые количества ресурсов.

В теории чисел гладким числом называется целое число, все простые делители которого малы.

В математическом анализе, и прилегающих разделах математики, ограниченное множество — множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай произвольного метрического пространства, а также на случай произвольного частично упорядоченного множества. Понятие ограниченности множества не имеет смысла в общих топологических пространствах, без метрики.

Минимальный автомат — это автомат, имеющий наименьшее возможное количество состояний и реализующий заданную функцию выходов. Задача минимизации автомата сводится к поиску его минимальной формы. Для произвольного конечного автомата может быть построен эквивалентный ему конечный автомат с наименьшим числом состояний.

В общей алгебре, термин кручение относится к элементам группы, имеющим конечный порядок, или к элементам модуля, аннулируемым регулярным элементом кольца.

Источник

Регулярный язык

В теории языков регуля́рным мно́жеством (или, регуля́рным языком) называется формальный язык, который удовлетворяет приведённым ниже свойствам. Эти простые свойства таковы, что класс регулярных множеств удобно изучать в целом и полученные результаты оказываются применимы во многих важных случаях формальных языков. То есть, понятие регулярного множества является примером математической структуры.

Определение регулярного множества

Пусть Σ — конечный алфавит. Регулярное множество R(Σ) в алфавите Σ определяется следующими рекурсивными свойствами:

№.	Свойство	Описание
1		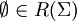Пустое множество является регулярным множеством в алфавите Σ
2		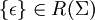Множество, состоящее из одной лишь пустой строки является регулярным множеством в алфавите Σ
3		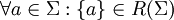Множество, состоящее из одного любого символа алфавита Σ является регулярным множеством в алфавите Σ
4		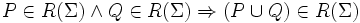Если два какие-либо множества являются регулярными в алфавите Σ, то и их объединение тоже является регулярным множеством в алфавите Σ
5		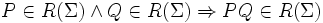Если два какие-либо множества являются регулярными в алфавите Σ, то и множество, составленное из всевозможных сцеплений пар их элементов тоже является регулярным множеством в алфавите Σ
6		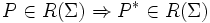Если какое-либо множество является регулярным в алфавите Σ, то множество всевозможных сцеплений его элементов тоже является регулярным множеством в алфавите Σ
Ничто другое, кроме следующего из перечисленного, не является регулярным множеством в алфавите Σ

См. также

Полезное

Смотреть что такое «Регулярный язык» в других словарях:

регулярный язык — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN regular language … Справочник технического переводчика

РЕГУЛЯРНЫЙ — (лат. regularius, от regula правило). Правильный, правильно устроенный, сделанный. Регулярный ход машины. Равномерный ход. Регулярная жизнь. Правильная, порядочная, однообразная жизнь. Словарь иностранных слов, вошедших в состав русского языка.… … Словарь иностранных слов русского языка

регулярный — См … Словарь синонимов

Язык кечуа — Кечуа Самоназвание: Qhichwa Simi, Runa Simi Страны: Аргентина, Боливия, Колумбия, Перу, Чили, Эквадор Регионы: Анды Официальный статус: Перу … Википедия

Древнеписьменный язык — Язык с давними письменными традициями, т. е. получивший письменность, приспособленную к структуре данного языка, несколько веков тому назад, причем функционирование письменного варианта языка носило не эпизодический, а регулярный характер, при… … Словарь социолингвистических терминов

Кечуа (язык) — У этого термина существуют и другие значения, см. Кечуа. Кечуа Самоназвание: Qhichwa Simi, Runa Simi Страны … Википедия

КАРКАС РЕГУЛЯРНЫЙ — каркас здания с сеткой колонг или стоек, основанной на шаге одного размера (Болгарский язык; Български) равномерен скелет (Чешский язык; Čeština) pravidelný skelet (Немецкий язык; Deutsch) regelmäßiges Skelett (Венгерский язык; Magyar) szabályos… … Строительный словарь

ПАРК РЕГУЛЯРНЫЙ — [ПАРК ФРАНЦУЗСКИЙ] парк, имеющий геометрически правильную планировку, обычно осевую схему (Болгарский язык; Български) френски парк (Чешский язык; Čeština) francouzský park (Немецкий язык; Deutsch) regelmäßiger Park; französischer Park… … Строительный словарь

Кечуа язык — Кечуа Самоназвание: Qhichwa Simi, Runa Simi Страны: Аргентина, Боливия, Колумбия, Перу, Чили, Эквадор Регионы: Анды Официальный статус: Перу … Википедия

Тагальский язык — (тагал, тагала, тагало; тагалог) один из филиппинских языков. Ареал первоначального распространения приходится на самый важный в политическом, экономическом и культурном отношении регион Республики Филиппины центральные и южные части острова… … Лингвистический энциклопедический словарь

Источник

Регулярные языки и конечные автоматы

Регулярные выражения и языки

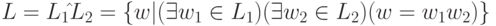
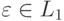
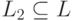
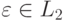
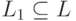
Тогда , т.е. конкатенация языков состоит из конкатенаций всех слов первого языка со всеми словами второго языка. В частности, если , то , а если , то .

Введем обозначения для «степеней» языка L :

Итерацию (L) * языка L образуют все слова которые можно разбить на несколько подряд идущих слов из L :

Ее можно представить с помощью степеней:

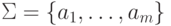
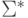
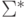
Отметим также, что если рассматривать алфавит как конечный язык, состоящий из однобуквенных слов, то введенное ранее обозначение для множества всех слов, включая и пустое, в алфавите соответствует определению итерации этого языка.

В следующей таблице приведено формальное индуктивное определение регулярных выражений над алфавитом и представляемых ими языков.

Нетрудно проверить, например, такие свойства регулярных операций:

Рассмотрим несколько примеров регулярных выражений и представляемых ими языков.

Пример 5.2. Регулярное выражение (0 +1) * представляет множество всех слов в алфавите <0, 1>.

Пример 5.3. Регулярное выражение 11(0 +1) * 001 представляет язык, состоящий из всех слов в алфавите <0, 1>, которые начинаются на ’11’, а заканчиваются на ‘001’.

Пример 5.4. Регулярное выражение 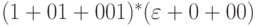представляет язык, состоящий из всех слов в алфавите <0, 1>, которые не содержат подслово ‘000’ ( см. задачу 5.3).

Источник

Истинное могущество регулярных выражений

«Ты не можешь парсить HTML с помощью регулярных выражений, потому что HTML не является регулярным. Используй XML парсер, и будет тебе счастье»

Что же на самом деле означает «регулярный»?

В контексте теории формальных языков что-то называется «регулярным», когда оно имеет грамматику, в которой любое правило вывода имеет одну из следующих форм:

Всё это, возможно, звучит несколько абстрактно, поэтому давайте рассмотрим пример: определение натуральных чисел как грамматики.

Эта грамматика говорит о том, что:

В этом примере цифры от 0 до 9 будут терминалами (поскольку их нельзя разбить на составляющие), а N будет единственным нетерминалом (поскольку его можно разделять дальше).

Другой момент, на который вы могли обратить внимание, это то, что несмотря на описание грамматикой таких простых вещей, она уже весьма раздута. Разве не было бы лучше, если бы мы могли выразить ту же концепцию, но в более сжатой форме?

И тут на сцену выходят регулярные выражения: грамматика выше эквивалентна регэкспу 7+ (который чертовски проще). И преобразование такого типа можно применить к любой регулярной грамматике: каждая из них имеет соответствующее регулярное выражение, описывающее все допустимые для неё строки.

Что могут описывать регулярные выражения

Итак, возникает закономерный вопрос: регулярные выражения могут описывать только регулярные грамматики, или они способны на большее? Ответом на него будет и да, и нет.

Регулярные выражения в смысле формальных грамматик могут (по определению) описывать только регулярные грамматики и ничего более.

Но когда программисты говорят о «регулярных выражениях», они не подразумевают формальные грамматики. Они говорят о производных регулярных выражениях, реализованных в их языках программирования. И эти реализации регэкспов весьма поверхностно связаны с изначальным понятием регулярности.

Любая современная разновидность регэкспов может описывать гораздо больше, чем просто регулярные языки. Уточнение того, насколько больше, — тема дальнейшего повествования.

Для сохранения простоты, я сфокусируюсь только на PCRE-реализации регэкспов. Просто потому, что я знаю её лучше всего (поскольку она используется в PHP). Множество прочих реализаций весьма с ней схожи, поэтому большую часть нижеизложенного можно применить и к ним тоже.

Иерархия языков

Для анализа того, что можно, а что нельзя описать с помощью регулярных выражений, прежде всего рассмотрим, какие ещё существуют типы языков. Хорошей точкой отсчёта для этого будет иерархия Хомского:

Как видите, она делит формальные языки на четыре типа: регулярные языки (тип 3) — наименее мощные, за которыми следуют контекстно-свободные языки (тип 2), контекстно-зависимые языки (тип 1) и, наконец, всемогущие неограниченные языки (тип 0).

Иерархия Хомского — контейнерная, поэтому маленькие коробочки на картинке полностью заключены в большие коробки. Т.е. любой регулярный язык является также контекстно-свободным (но не наоборот!).

Итак, давайте поднимемся на ступеньку вверх по иерархии. Мы уже знаем, что регулярным выражением можно описать любой регулярный язык. А возможно ли это для контекстно-свободных языков?

(Напоминание: когда я говорю «регулярные выражения», я подразумеваю их в программистском смысле, а не в смысле теории формальных языков).

Описание контекстно-свободных языков

Ответ на вопрос выше: да, возможно!

Следовательно, регулярные выражения способны описывать как минимум некоторые не регулярные, контекстно-свободные грамматики. Но могут ли они описать их все? Чтобы ответить на этот вопрос, посмотрим прежде на определение контекстно-свободных грамматик.

В контекстно-свободной грамматике все правила вывода имеют вид:

Здесь A — снова нетерминальный символ, а β — произвольная строка из терминалов и нетерминалов. Таким образом, каждое правило контекстно-свободной грамматики имеет нетерминал в левой части и строку из произвольных символов справа.

В качестве примера рассмотрим следующую грамматику:

Это отрывок из PHP-грамматики (всего лишь несколько простых правил). Синтаксис немного отличается от того, что мы использовали раньше, но его можно легко понять. Один из аспектов, который стоит отметить, состоит в том, что имена T_SOMETHING здесь также являются терминальными символами. Такие символы обычно называют токенами, они кодируют собой более абстрактные понятия. Например, T_FUNCTION представляет из себя ключевое слово function, а T_STRING — токен-метка (подобно getUserById или some_other_name).

Я использую этот пример, чтобы продемонстрировать одну вещь: контекстно-свободные грамматики уже достаточно мощны, чтобы кодировать достаточно сложные языки. Вот почему почти все языки программирования имеют контекстно-свободные грамматики. В этот перечень входит и синтаксически корректный HTML.

Возвращаясь к актуальному вопросу: так могут ли регулярные выражения связывать все контекстно-свободные грамматики? Снова ответ: да!

Это чрезвычайно легко доказать, поскольку регулярные выражения (по крайней мере, PCRE и ему подобные) предоставляют синтаксис для построения грамматик, очень похожий на приведённый выше:

То, что вы видите выше — это регулярное выражение для описания e-mail адреса с помощью RFC 5322. Оно построено с помощью простого преобразования БНФ-правил из RFC в нотацию, которую понимает PCRE.

Синтаксис чрезвычайно прост: все определения правил оборачиваются в DEFINE-утверждение, которое в основном означает, что все эти правила не должны непосредственно чему-то соответствовать, их достаточно просто декларировать. Только часть ^(?&addr_spec)$ в самом конце определяет, что же в конце-концов тут описывается.

Таким образом, приведённый выше синтаксис позволяет просто отобразить грамматику на регулярное выражение:

Единственная загвоздка в том, что регулярные выражения не поддерживают левостороннюю рекурсию. Т.е., если взять приведённое выше определение списка параметров:

Вы не сможете в точности конвертировать его в основанный на грамматике регэксп. Следующее не сработает:

Причина этого в том, что non_empty_parameter_list появляется в крайней левой части своего собственного определения. Это называется левосторонней рекурсией и очень часто встречается в определениях грамматик. Причина в том, что LALR(1) парсеры, которые чаще всего используются для разбора, обычно обрабатывают левостороннюю рекурсию лучше, чем правостороннюю.

Но не пугайтесь, это не в коей мере не влияет на мощь регулярных выражений. Каждая леворекурсивная грамматика может быть преобразована в праворекурсивную. В примере выше достаточно просто поменять местами две части:

Теперь должно быть абсолютно ясно, что регулярные выражения способны описывать любой контекстно-свободный язык (и, следовательно, почти все языки, с которыми сталкиваются программисты). Единственная проблема: несмотря на то, что регулярные выражения могут описывать контекстно-свободные грамматики, они обычно не могут разбирать их. Разбор подразумевает преобразование какой-либо строки в абстрактное синтаксическое дерево. Для этого невозможно использовать регулярные выражения, по крайней мере PCRE (хотя, конечно, в Perl’e, где есть возможность вставлять произвольный код в регулярное выражение, вы можете практически всё. ).

А сейчас позвольте мне снова заострить внимание на том, о чём я мимоходом упоминал ранее: синтаксически корректный HTML — контекстно-свободен. Следовательно, вы можете описывать его, используя регулярные выражения, в противовес распространённому мнению. Просто не забывайте о двух вещах: во-первых, большая часть HTML, с которым вы сталкиваетесь, не синтаксически корректная (обычно, она даже не является закрытой). И во-вторых, только то, что вы можете, не означает, что вы должны. Вы можете писать свой софт на Brainfuck, однако существуют причины, почему вы этого не делаете, верно?

Моё мнение по теме таково: где бы вы не нуждались в общей HTML-обработке, используйте DOM-библиотеку на свой вкус. Она правильно обработает некорректный HTML и примет на себя всю тяжесть разбора. С другой стороны, если вы имеете дело со специфическими случаями, то быстрые регулярные выражения часто наилучший выход. И я должен признаться: хотя я обычно говорю людям не разбирать HTML с помощью регулярных выражений, сам я, как известно, делаю это частенько. Просто потому, что часто сталкиваюсь со специфическими ситуациями, когда использовать регэкспы элементарно проще.

Контекстно-зависимые грамматики

Теперь, когда мы подробно рассмотрели контекстно-свободные языки, давайте поднимемся вверх на ещё одну ступеньку в иерархии Хомского: к контекстно-зависимым языкам.

Для них структурные правила будут иметь следующую форму:

Чтобы сделать изложенное более понятным, попробуем интерпретировать следующие правила:

По-русски это будет звучать так:

Заменить `A` на `c`, но только в том случае, если у него имеется `a b` слева.
Заменить `B` на `Q H`, но только в том случае, если у него имеется `a` слева и `c` справа.
Заменить `B` на `C`, но только если у него есть `H` слева.

Контекстно-зависимые языки — это то, что вы редко встретите в «нормальном» программировании. Они более важны в области обработки естественных языков (поскольку естественные языки определённо не являются контекстно-свободными. Слова имеют различное значение в зависимости от контекста). Но даже люди, занимающиеся обработкой естественных языков, работают с так называемыми «мягко контекстно-зависимыми языками», поскольку для моделирования их достаточно, а разбор происходит намного быстрее.

Для понимания того, насколько могуществены контекстно-зависимые грамматики, давайте рассмотрим другой класс грамматик, обладающий точно такой же выразительной силой, как и контекстно-зависимые: неукорачивающие грамматики.

Эти отношения (эквивалентные для контекстно-зависимых и неудлиняющих грамматик) делают абсолютно ясным, что с помощью контекстно-зависимых грамматик вы можете практически всё. Просто не укорачивайте 🙂

Чтобы получить понятие, почему обе грамматики имеют одинаковую выразительную силу, посмотрите на следующий пример преобразований:

Ладно, вернёмся к регулярным выражениям. Могут ли они так же описывать и контекстно-зависимые языки?

На этот раз я не смогу вам дать определённого ответа. Конечно, они могут описывать некоторые контекстно-зависимые языки, но я понятия не имею, могут ли они описывать их все.

PCRE-регэксп для этого языка следующий:

В приведённом выше регэкспе вы также можете увидеть, как реализована концепция контекста в регулярных выражениях с использованием утверждений. Если мы теперь вернёмся к определению контекстно-зависимой грамматики, то вы можете сказать, что правило вывода вида

можно преобразовать в следующее DEFINE-правило регэкспов:

Но факт невозможности прямого преобразования контекстно-зависимой грамматики в регэксп сам по себе не означает, что регулярные выражения на могут описывать их все. Например, приведённый выше язык 0> тоже имеет грамматику, которая требует ретроспективного утверждения переменной ширины. Может быть, что-то подобное возможно и для других контекстно-зависимых грамматик. Я честно не знаю.

Так что же мы в конце-концов можем сказать? Регэкспы могут описывать как минимум некоторые контекстно-зависимые языки, но неизвестно, способны ли они описать их все.

Неограниченные грамматики

Следующий класс грамматик в иерархии Хомского — неограниченные грамматики. В набор языков, которые могут формироваться с их помощью, входят все рекурсивно-перечислимые языки.

Насколько в точности сильны неограниченные грамматики? Настолько, что сильнее их не бывает: они Тьюринг-полны. Существует даже «язык программирования», основанный на неограниченных грамматиках: Thue. Поскольку он Тьюринг-полный, то может делать всё, на что способны остальные языки программирования.

Одним из следствий Тьюринг-полноты является то, что проблема проверки на принадлежность определённой строки некоторой грамматике в общем случае неразрешима.

К сожалению, я не могу рассказать ещё что бы то ни было о том, как связаны регулярные выражения и неограниченные грамматики. Чёрт, я даже не смог найти пример адекватной неограниченной грамматики (которая не была бы неукорачивающей).

Но сейчас, поскольку мы заговорили о Тьюринг-полноте, перейдём к следующему моменту:

Регулярные выражения с обратными ссылками являются NP-полными

Вот ещё одно очень мощное свойство регулярных выражений, о котором я не упоминал ранее: обратные ссылки.

Т.е. содержащие вот такой очень простой регэксп:

То, что этот регэксп описывает, называется «языком копий» и является ещё одним типичным примером контекстно-зависимых языков.

Аналогичным образом вы можете описать с помощью обратных ссылок прочие примеры грамматик, приведённые выше:

Объяснение того, как это работает, выходит за рамки данной статьи, но вы можете прочитать об этом прекрасный топик на StackOverflow.

Как видите, простое добавление обратной ссылки (без поддержки рекурсивной подмаски) уже увеличивает силу регулярных выражений. Оно в принципе настолько могущественно, что делает описание регулярными выражениями NP-полной задачей.

Что означает «NP-полная»? NP-полнота — это один из классов в теории сложности вычислений для решения задач, в который впадают многие «тяжёлые» проблемы. Примерами NP-полных задач являются задача коммивояжера (TSP), задача выполнимости булевых формул (SAT) и задача о ранце (BKP).

Другое важное условие для того, чтобы называть задачу NP-полной, это возможность свести к ней любую другую NP-задачу. Таким образом, все NP-полные задачи в основном взаимозаменяемы. Если найдёте быстрое решение одной из них, то вы будете иметь быстрое решение для них всех.

Так что если кто-то найдёт быстрое решение для NP-полной задачи, то практически все сложные вычислительные задачи человечества будут решены одним махом. Что, как мы знаем, будет означать конец цивилизации.

Чтобы доказать, что регулярные выражения с обратными ссылками в точности NP-полны, можно просто взять одну из хорошо известных NP-полных задач и доказать, что она может быть решена с помощью использования регулярных выражений. В качестве примера я выбрал 3-CNF SAT задачу.

3-CNF SAT расшифровывается как «Задача выполнимости булевых формул в 3-конъюнктивной нормальной форме» и достаточно проста для понимания. Имеется булева формула следующего вида:

Она состоит из ряда условий, разделённых операторами И. Каждое из этих условий состоит из трёх переменных (или их отрицаний), разделённых операторами ИЛИ. 3-CNF SAT спрашивает: существует ли решение у этой булевой формулы (например, истина)?

Приведённую выше булеву формулу можно преобразовать в следующее регулярное выражение:

Теперь дело за движком. Он проверяет различные пути для связывания строки до тех пор, пока или решение не будет найдено, или он не сдастся.

Подводя итог

Но не забывайте: из того, что вы можете, не следует, что вы должны. Обработка HTML с помощью регулярных выражений — действительно плохая идея в некоторых случаях. А в других — это, возможно, лучшее, что можно сделать.

Просто прикиньте, каково простейшее решение для вашей конкретной задачи, и используйте его. Если вы выберите решать задачу с помощью регулярных выражений, не забывайте о x-модификаторе, который позволяет вам сделать более красивым формат ваших регэкспов. Для сложных регулярных выражений так же не забывайте использовать DEFINE-утверждения и именованные подмаски, чтобы сохранить ваш код чистым и читаемым.

От переводчика: возможные замечания по поводу перевода, пожалуйста, пишите в личку. Я буду за них очень признательна.

Источник