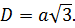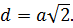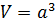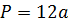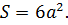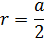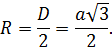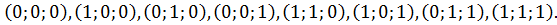что такое ребра в геометрии
Значение слова «ребро»
1. Дугообразная узкая кость, идущая от позвоночника к грудной кости. Под мокрой прилипшей шерстью [щенка] проступали ребра. Новиков-Прибой, Два друга.
2. Узкий край или узкая сторона какого-л. предмета. Ребро доски. Ребро монеты. □ Завалишин свирепо и звонко ударил вытянутым пальцем о ребро стола. Куприн, Корь. — Как вы кирпичи кладете. Надо плашмя, а вы на ребро. Караваева, Родной дом.
3. Место пересечения двух плоскостей. Ребро пирамиды. □ Его толкнули в плечо острым ребром солдатского походного сундучка. Федин, Необыкновенное лето.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
РЕБРО’, а́, мн. рёбра, рёбер, рёбрам, ср. 1. Дугообразная узкая кость, прикрепленная сзади к позвоночнику и идущая к грудной кости. У человека семь верхних и пять нижних, или ложных, ребер. Так похудел, что ребра видно. 2. Линия пересечения двух плоскостей (мат.). Р. многогранника. Р. двугранного угла. || Узкий край или сторона предмета (по его длине). Поставь кирпич стоймя или на р. Положи доску ребром. Р. монеты. Он ударил правой рукою — не ладонью, а ребром руки — по столу. Тургенев. ◊
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
ребро́
1. анат. дугообразная па́рная плоская кость позвоночного животного, идущая от позвоночника к грудине и являющаяся частью грудной клетки ◆ На рентгеновском снимке видны рёбра. ◆ Перелом ребра.
2. край тонкого плоского предмета ◆ Монетка упала на ребро и покатилась.
3. геометр. отрезок прямой, образованный пересечением двух граней многогранника ◆ Требуется построить октаэдр, для которого заданы координаты вершин и параметры рёбер. В. А. Овчинников, «Применение генетических алгоритмов в задачах синтеза кузова автомобиля», 2004 г. // «Информационные технологии» (цитата из НКРЯ)
4. матем. часть графа, кортеж из двух вершин, а также его изображение в виде отрезка либо дуги, соединяющей два узла ◆ Если все рёбра различны, то маршрут называется цепью; если все вершины (а значит, и рёбра) различны, то маршрут называется простой цепью. (цитата из библиотеки Google Книги)
5. перен. истор. мн. ч. пластинка с аудиозаписью, изготовленная из полимерного листа, использованного ранее для получения рентгеновского снимка ◆ Записи оркестра «на рёбрах».
6. техн. длинный, относительно неширокий выступ на поверхности чего-либо ◆ Для отделки монументальных порталов и рёбер всего комплекса был выбран чередующийся с белой флорентийской штукатуркой серый камень, привезённый с каменоломен в долине Мензолы, ценный до такой степени, что его можно было получить по специальной лицензии правителя. (цитата из библиотеки Google Книги)
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова нитрокраска (существительное):
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок № 13. Многогранники
Перечень вопросов, рассматриваемых в теме:
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников.
Грани многогранника – многоугольники, ограничивающие многогранники.
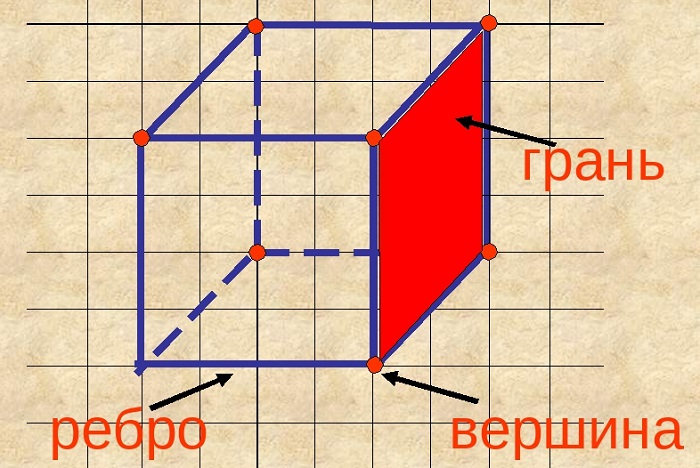
Ребра многогранника – стороны граней многогранника.
Вершины многогранника – концы ребер многогранника (вершины граней многогранника).
Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.
Выпуклый многогранник – многогранник, расположенный по одну сторону от плоскости его любой грани.
Невыпуклый многогранник – многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.
Атанасян Л. С., В. Ф. Бутузов, С. Б. Кадомцев и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. Для общеобразоват. организаций: базовый и углубл. уровния. – М.: Просвещение, 2014. – 255 с. (стр. 58, стр. 60 – 61)
Долбилин Н. П. Жемчужины теории многогранников М. : – МЦНМО, 2000. – 40 с.: ил. (стр. 27 – 31)
Открытые электронные ресурсы:
Долбилин Н. П. Три теоремы о выпуклых многогранниках. Журнал Квант.
Теоретический материал для самостоятельного изучения
К определению понятия многогранника существует два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в планиметрии под многоугольником мы понимали замкнутую линию без самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно рассматривать как часть плоскости, ограниченную этой линией, включая ее саму (рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть плоская поверхность.
Б)
Рисунок 1 – разные подходы к определению многоугольника
Вторая трактовка понятия определяет многогранник как геометрическое тело, ограниченное конечным числом плоских многоугольников.
В дальнейшем, мы будем использовать вторую трактовку понятия многогранника.
Уже известные вам тетраэдр и параллелепипед являются многогранниками. Потому что они являются геометрическими телами, ограниченные конечным числом плоских многоугольников. Еще один пример многогранника — октаэдр (рис. 2)
Рисунок 2 – изображение октаэдра
Многоугольники, ограничивающие многогранник, называются его гранями. Так, у тетраэдра и октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».
Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. В остальных случаях многогранник называется невыпуклым (рис.3).
Рисунок 3 – Виды многогранников
Сумма плоских углов при вершине выпуклого многогранника
Рисунок 4 – сумма плоских углов пи вершине многогранника
Теорема Эйлера. Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.
Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.
Примеры и разбор решения заданий тренировочного модуля
Задание 1. Какие из перечисленных объектов НЕ могут быть элементами многогранника? Укажите номера в порядке возрастания.
Элементы многогранника, которые мы выделили: ребра, грани, вершины и диагонали. Ребро и диагональ многогранника – это отрезок. Грань многогранника – многоугольник, или иначе ограниченная часть плоскости. Вершины представляют собой точки. Таким образом, элементами многогранника не могут быть плоскость, луч, многогранник, прямая.
Задание 2. Сопоставьте геометрическим фигурам их вид
Б) пространственная фигура
Вспомним, что изобразить пространственную фигуру можно разными способами. Например, с помощью теней или изображением невидимых линий пунктиром. Так, среди всех изображений плоской фигурой является фигура под номером 1.
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников. Только на изображении 2 фигура ограничена многоугольниками. Таким образом, получаем следующий ответ: 1-А, 2-В, 3-Б
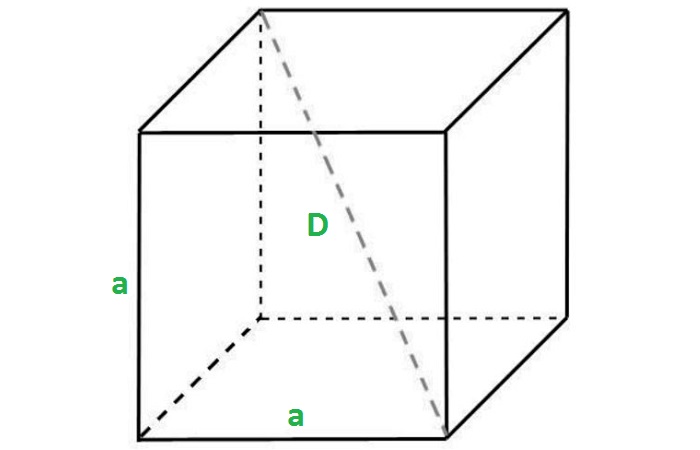
Что такое куб: определение, свойства, формулы
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
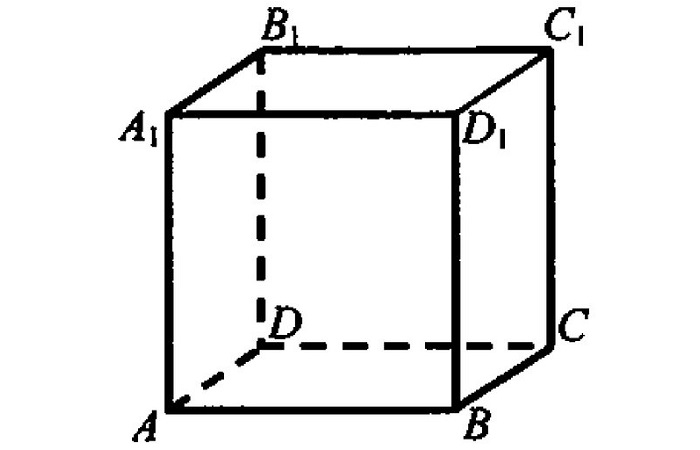
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
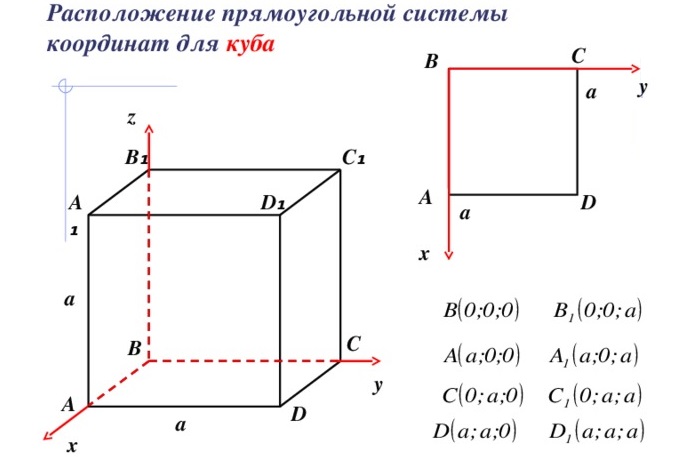
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Ребро – что означает? Определение, значение, примеры употребления
Ищешь, что значит слово ребро? Пытаешься разобраться, что такое ребро? Вот ответ на твой вопрос:
Значение слова «ребро» в словарях русского языка
Ребро это:
ребро́ (, ) — одна из парных дугообразных плоских костей, идущих от позвоночника к грудине и составляющих грудную клетку у позвоночных животных.
У человека 12 пар рёбер.
Ребро
1.Дугообразная узкая кость, прикрепленная сзади к позвоночнику и идущая к грудной кости. отт. перен. Часть остова какого-либо сооружения, дугообразно изогнутая и поддерживающая, скрепляющая собою что-либо.
Ребро
ср.
1) а) Дугообразная узкая кость, прикрепленная сзади к позвоночнику и идущая к грудной кости. б) перен. Часть остова какого-л. сооружения, дугообразно изогнутая и поддерживающая, скрепляющая собою что-л.
2) а) Линия пересечения двух плоскостей. б) Узкий край или сторона предмета (по его длине).
Ребро
Ребро
Ребро
В геометрии: отрезок прямой, лежащий на пересечении двух граней многогранника ребро дугообразно изогнутая скрепляющая часть остова какого-нибудь сооружения Spec ребро одна из парных дугообразных плоских костей, идущих от позвоночника к грудной кости и составляющих грудную клетку Грудинные ребра. Шейное р. Поясничное р. Один ребра остались у кого-н. (перен. : очень исхудал; разг.). Пересчитать ребра кому-н. (перен. : поколотить; прост.). ребро узкий край или сторона предмета Поставить доску на р.
Ребро
Ребро
ребро ср.
1) а) Дугообразная узкая кость, прикрепленная сзади к позвоночнику и идущая к грудной кости. б) перен. Часть остова какого-л. сооружения, дугообразно изогнутая и поддерживающая, скрепляющая собою что-л.
2) а) Линия пересечения двух плоскостей. б) Узкий край или сторона предмета (по его длине).
Ребро
ребра, мн. рёбра, рёбер, рёбрам, ср.
1. Дугообразная узкая кость, прикрепленная сзади к позвоночнику и идущая к грудной кости. У человека семь верхних и пять нижних, или ложных, ребер. Так похудел, что ребра видно.
2. Линия пересечения двух плоскостей (мат.). Ребро многогранника. Ребро двугранного угла. || Узкий край или сторона предмета (по его длине). Поставь кирпич стоймя или на ребро. Положи доску ребром. Ребро. монеты. Он ударил правой рукою – не ладонью, а ребром руки – по столу. Тургенев. Поставить ребром (последнюю копейку) (разг.) – истратить (все деньги) на что-н. или рискнуть в игре. Поставить ребром (вопрос и т. п.) – заявить категорически, прямо, не допуская увиливания. – Какой вы однако напористый! Всякое слово ребром ставите. Салтыков-Щедрин. пересчитать рёбра кому (простореч.) – то же, что пересчитать кости, см. кость.
Ребро
многогранника, сторона его грани.
Ребро
ребро, —а, мн. рёбра, рёбер, рёбрам
Ребро
Где и как употребляется слово «ребро»?
Кроме значения слова «ребро» в словарях, рекомендуем также ознакомиться с примерами предложений и цитат из классической литературы, в которых употребляется слово «ребро».
Так вы сможете гораздо легче понять и запомнить, как правильно употребляется слово «ребро» в тексте и устной речи.
Примеры употребления слова «ребро»
Волосы рыжие развеваются, как у ведьмы, куцая курточка посюда, – свидетель провёл ребром ладони по талии, – юбка короче некуда, прости господи.
Сломанные рёбра протестующе заныли, да так, что на глаза навернулись слёзы.
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
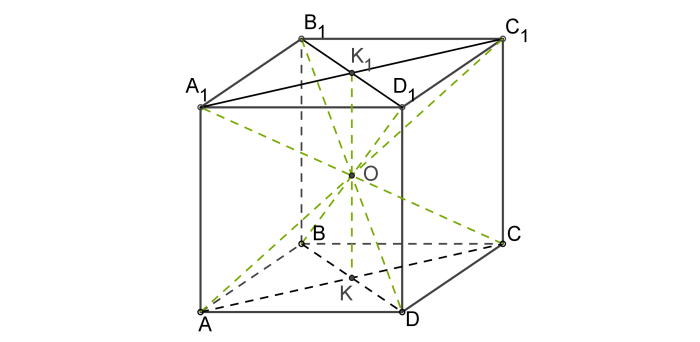
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
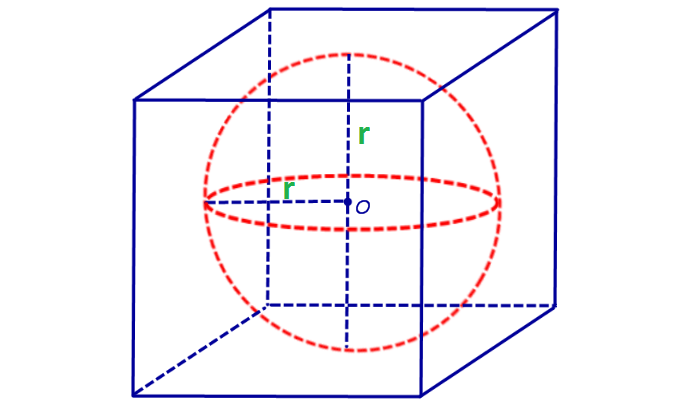
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
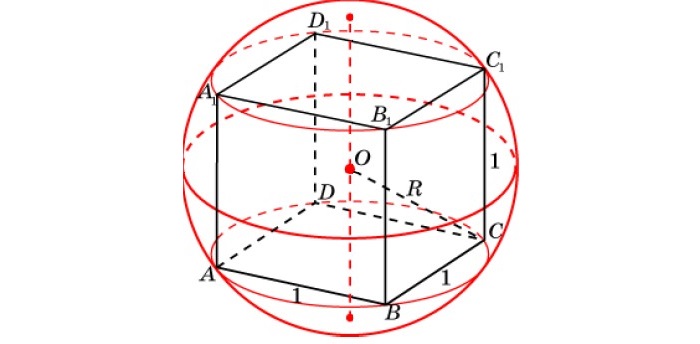
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
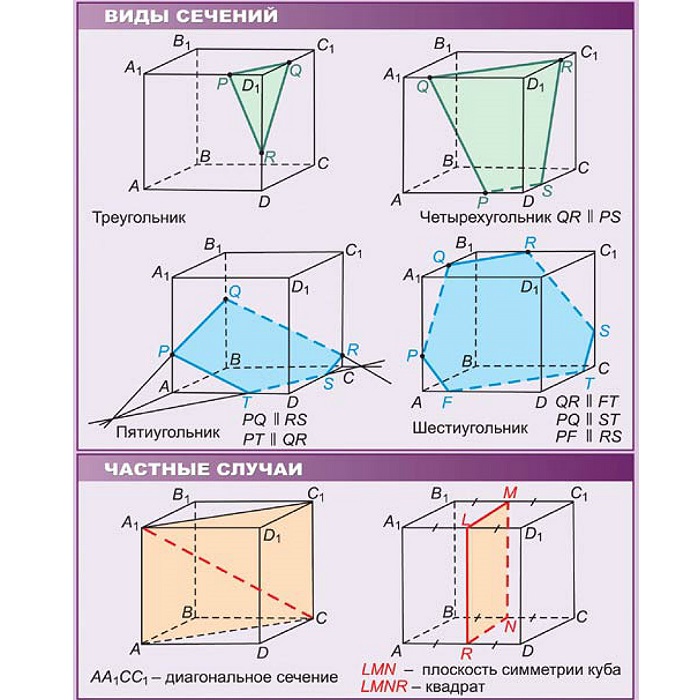
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.